火车进出栈问题 题解
来源 卡特兰数
个人评价(一句话描述对这个题的情感)
…~%?..,# *'☆&℃$︿★?
1 题面
一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。
输入
一个数,n(n<=60000)
输出
一个数s表示n节车厢出栈的可能排列方式
样例
样例输入1
3
样例输出1
5
2 分析题面
求卡特兰数的第n项,不取模
有两种方式,都能推出这是一道纯卡特兰数题
2.1 递推
“计数原理中的乘法原理,总的方案数等于第一步的方案数和第二步的方案数之积”
以编号为 kkk 的车厢为界,将列车分为两部分
一部分是在第 kkk 节车厢出栈前出栈的车厢,一部分是在第 kkk 节车厢出栈后出栈的车厢
设在第kkk节车厢出栈前出栈的车厢的数量为 i(0<=i<=k)i(0<=i<=k)i(0<=i<=k)
则在第 kkk 节车厢出栈后出栈的车厢的数量为 (k−i−1)(k-i-1)(k−i−1)
前 iii 节车厢出栈的可能性数量有 F(i)F(i)F(i)
后 (n−i−1)(n-i-1)(n−i−1) 节车厢出栈的可能性数量有 F(k−i−1)F(k-i-1)F(k−i−1)
所以总的数量为 F(i)×F(k−i−1)F(i)\times F(k-i-1)F(i)×F(k−i−1)
由于当只有0节车厢(即一节车厢也没有)时,方案数为111
所以,F(0)=1F(0)=1F(0)=1
因此,我们可以得到一个递归公式:
F(k)=F(0)×F(k−1)+F(1)×F(k−2)+F(2)×F(k−3)+...+F(k−2)×F(1)+F(k−1)×F(0)F(k)=F(0)\times F(k-1)+F(1)\times F(k-2)+F(2)\times F(k-3)+...+F(k-2)\times F(1)+F(k-1)\times F(0)F(k)=F(0)×F(k−1)+F(1)×F(k−2)+F(2)×F(k−3)+...+F(k−2)×F(1)+F(k−1)×F(0)
其中k>=1,F(0)=1其中k>=1,F(0)=1其中k>=1,F(0)=1
看出什么了吗?
其实这道题就是Catalan number!!
只不过n的初值少111。。。
2.2 组合数
首先,每一种进出栈的顺序都与出栈序列一一对应
也就是说,如果我们用+1+1+1表示进栈,−1-1−1表示出栈
那么举个例子:
出栈序列 1,3,4,21,3,4,21,3,4,2 与进出栈顺序 +1,+1,−1,+1,+1,−1,−1,−1+1,+1,-1,+1,+1,-1,-1,-1+1,+1,−1,+1,+1,−1,−1,−1 是对应的
那么对nnn个数的序列,总的进出栈顺序不是就是给2n2n2n个111前面挑nnn个添加+++号
其他的添加−-−号,共C2nn{\rm C}_{2n}^nC2nn种吗?
答案是否定的,这是因为出栈的前提是有进栈
于是要求每个排列中的前若干项和均不为负数
即排列1,−1,−1,1,1,−1,−1,11,-1,-1,1,1,-1,-1,11,−1,−1,1,1,−1,−1,1是无效的
那么无效的排列到底有多少呢?
考虑MMM是所有无效的排列构成的集合
考虑其中第一次发现排列无效的时候,也就是第一次发现其前若干项和为−1-1−1的时候
此时我们将包含使得前若干项和为−1-1−1的这一项开始的之前的所有项全都取相反数
那么就会得到一个新的排列
这个排列包含n+1n+1n+1个+1+1+1,以及n−1n-1n−1个−1-1−1
设所有这样的排列构成集合NNN
显然,这个M→NM\to NM→N的映射是一一映射的
(NNN中的每一个排列从第一项往后累积求和的时候必然会出现和为+1+1+1的情形,
此时将排列中使得和为+1+1+1的这一项连同之前的所有项全部取相反数,
那么就会得到MMM中的一个排列)
因此无效的排列共有C2nn−1{\rm C}_{2n}^{n-1}C2nn−1个.
综上,所有不同的出栈序列总数为C2nn−C2nn−1{\rm C}_{2n}^n-{\rm C}_{2n}^{n-1}C2nn−C2nn−1,即C2nnn+1\dfrac {{\rm C}_{2n}^n}{n+1}n+1C2nn
也就是卡特兰数!
3 代码实现(注释)
3.1定义
//Cn为卡特兰数的第n项
int n;//输入
int ans[N];//高精度答案数组
int len=1;//答案的位数
int p[N];//质数
int c[N];//c[i]是Cn中p的个数
int tot;//2*n中质数的个数
bool vis[N];//埃氏筛标记数组
3.2 输入
就输入一个n
scanf("%d",&n);//输出的
3.3 预处理
预处理质数,这里我用的是埃氏筛(用欧拉筛也行)
for(int i=2;i<=n*2;i++) {//预处理1-2n之间的质数if(!vis[i]) {//vis数组没有被标记过p[++tot]=i;//统计质数for(int j=i;j<=N;j+=i) vis[j]=1;//大量优化复杂度!}//就是埃氏筛
}
3.4 高精度
这个乘法还是挺显然的吧
void jing(int x) {//高精乘法 乘xfor(int i=1;i<=len;i++) ans[i]*=x;//直接乘xlen+=6;//长度最多+6for(int i=1;i<=len;i++) {//每一位处理ans[i+1]+=ans[i]/10;ans[i]%=10;}//进位while(!ans[len]) len--;//将多加的长度剪掉
}
3.5 计算
先考虑(n)小一点的做法,我们可以直接用卡特兰数的线性递推公式:
fn=fn−14n−2n+1f_n=f_{n-1}\frac{4n-2}{n+1}fn=fn−1n+14n−2
然后看一眼数据,显然不行!
然后考虑一下优化
我们要换一个思路,应该用这个公式:
Cn=C2nnn+1C_n=\frac{C_{2n}^n}{n+1}Cn=n+1C2nn
大力感谢zjy提供的思路!!!
3.5.1 转换公式
首先,由卡特兰数的通项公式Cn=C2nnn−1C_n= \frac{C_{2n}^n}{n-1}Cn=n−1C2nn
⇒Cn=!(2n)/(!n)2n+1⇒Cn=!(2n)(!n)2(n+1)⇒C_n=\frac{!(2n)/(!n)^2}{n+1} \\ \ \\⇒C_n=\frac{!(2n)}{(!n)^2(n+1)}⇒Cn=n+1!(2n)/(!n)2 ⇒Cn=(!n)2(n+1)!(2n)
最终表示为阶乘形式:Cn=(2n)!n!(n−1)!C_n= \frac{(2n)!}{n!(n-1)!}Cn=n!(n−1)!(2n)!
再看一下算数基本定理:
A=p1a1∗p2a2∗...∗pkakA=p_1^{a_1}*p_2^{a_2}*...*p_k^{a_k}A=p1a1∗p2a2∗...∗pkak
注意到卡特兰数每一项都一定是一个整数
也就是说,如果将如上公式的分子分母分解质因数
那么分母的各个因式指数上一定是可以被分子的各个因式相减抵消的
但是分子分母都是存在阶乘结构的,那么就考虑然后对某个数的阶乘分解质因数
3.5.2 分解阶乘
其次,一个质数p[i]p[i]p[i]在n!n!n!中可分解的个数为n/p[i]n/p[i]n/p[i]
口胡一下证明:
n!=1×2×3×...×(n−1)×nn!=1\times 2\times 3\times... \times(n-1)\times nn!=1×2×3×...×(n−1)×n
所以在n!n!n!中(即1−n1-n1−n中)是p[i]p[i]p[i]的倍数的个数显然为n/p[i]n/p[i]n/p[i]个
然后,在n!n!n!中可被至少包含kkk的mmm次方的个数x[m]x[m]x[m]为:
x[m]=(2n)/p[i]m−n/p[i]m−(n−1)/p[i]mx[m]=(2n)/p[i]^m-n/p[i]^m-(n-1)/p[i]^mx[m]=(2n)/p[i]m−n/p[i]m−(n−1)/p[i]m
最终,CnC_nCn中包含p[i]p[i]p[i]的个数为
所有nnn能被p[i]mp[i]^mp[i]m整除的mmm的x[m]x[m]x[m]之和
所以c[i]=∑j=1mx[j]c[i]=\sum^m_{j=1}x[j]c[i]=∑j=1mx[j]
口胡证明如下:
证明1:
不妨设k3∣n!k^3|n!k3∣n!且最多只能被kkk的3次方整除
当m=1m=1m=1时,x[1]=(2n)/k−n/k−(n−1)/kx[1]=(2n)/k-n/k-(n-1)/kx[1]=(2n)/k−n/k−(n−1)/k
当m=2m=2m=2时,x[2]=(2n)/k2−n/k2−(n−1)/k2x[2]=(2n)/k^2-n/k^2-(n-1)/k^2x[2]=(2n)/k2−n/k2−(n−1)/k2
当m=2m=2m=2时,x[3]=(2n)/k3−n/k3−(n−1)/k2x[3]=(2n)/k^3-n/k^3-(n-1)/k^2x[3]=(2n)/k3−n/k3−(n−1)/k2
由于xxx数组的定义是x[m]x[m]x[m]是n!n!n!(即1−n1-n1−n)中至少包含kkk的mmm次方的数的个数
所以,n!n!n!中只包含k的1次方的数的个数为x[1]−x[2]x[1]-x[2]x[1]−x[2]
同理可得,n!n!n!中只包含k的1次方的数的个数为x[2]−x[3]x[2]-x[3]x[2]−x[3]
又因为n!n!n!且最多只能被kkk的3次方整除,所以n!n!n!中只包含k的1次方的数的个数为x[3]x[3]x[3]
所以总的包含的kkk的个数ccc为
c=(x[1]−x[2])×1+(x[2]−x[3])×2+x[3]×3c=(x[1]-x[2])\times1+(x[2]-x[3])\times2+x[3]\times3c=(x[1]−x[2])×1+(x[2]−x[3])×2+x[3]×3
化简后得:c=x[1]+x[2]+x[3]c=x[1]+x[2]+x[3]c=x[1]+x[2]+x[3]
根据数学归纳法,
c[i]=∑j=1mx[j]c[i]=\sum^m_{j=1} x[j]c[i]=∑j=1mx[j]
证毕
证明2:
对于n!=1×2×...×nn!=1\times2\times...\times nn!=1×2×...×n,考虑它存在多少个质因子ppp
- 显然有⌊np⌋\lfloor\frac{n}{p}\rfloor⌊pn⌋个数有至少111个因子ppp
- 那么,有⌊np2⌋\lfloor\frac{n}{p^2}\rfloor⌊p2n⌋个数有至少222个因子ppp
- .........
- 依次类推,有⌊npx⌋\lfloor\frac{n}{p^x}\rfloor⌊pxn⌋个数有至少xxx个因子ppp
循环枚举每一个质因子,对于每一个质因子
所以我们通过枚举1−2n1-2n1−2n的质数来进行拆分
再将拆分出的p[i]c[i]p[i]^{c[i]}p[i]c[i]乘进ansansans中
就ok了
可得代码:
for(int i=1;i<=tot;i++) {//枚举质数int now=p[i];while(now<=n*2) {//c[i]指出现的个数c[i]+=n*2/now-n/now-(n+1)/now;now*=p[i];}while(c[i]--) jing(p[i]);//乘p[i]的c[i]次方
}
3.6 输出
输出高精ans数组即可
for(int i=len;i>=1;i--) {printf("%d",ans[i]);
}//注意要倒着输出
3.7 总体代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1200000;
int n,ans[N],len=1,p[N],c[N],tot;
bool vis[N];
void jing(int x) {for(int i=1;i<=len;i++) ans[i]*=x;len+=6;//最多加六位(*的数小于等于n*2)for(int i=1;i<=len;i++) {ans[i+1]+=ans[i]/10;ans[i]%=10;}while(!ans[len]) len--;
}//高精度乘法
int main(){scanf("%d",&n);//初始化ans[1]=1;//初始化高精ans=1for(int i=2;i<=n*2;i++) {if(!vis[i]) {p[++tot]=i;//统计质数for(int j=i;j<=N;j+=i) vis[j]=1;//排除合数//原因显然,质数的k(k≠1)倍肯定不是质数,证明如下://质数的定义是:一个数只有1和它本身两个因数,称这个数叫做质数//质数(p[i])的k(k≠1)倍已经有了k和p[i]两个(不是1和它本身)的因数//综上所述,质数的k(k≠1)倍肯定不是质数}//埃氏筛求2*n以内的质数} //预处理for(int i=1;i<=tot;i++) {//枚举质数int now=p[i];while(now<=n*2) {//c[i]指出现的个数c[i]+=n*2/now-n/now-(n+1)/now;now*=p[i];}while(c[i]--) jing(p[i]);//高精乘法}//计算for(int i=len;i>=1;i--) {printf("%d",ans[i]);}//输出return 0;
}
4 总结
就是卡特兰数高精的一种奇妙并且码量少的一种写法!
完结撒花❀
★,°:.☆( ̄▽ ̄)/$:.°★ 。
相关文章:

火车进出栈问题 题解
来源 卡特兰数 个人评价(一句话描述对这个题的情感) …~%?..,# *☆&℃$︿★? 1 题面 一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。 输入…...
Unity学习日记12(导航走路相关、动作完成度返回参数)
目录 动作的曲线与函数 创建遮罩 导航走路 设置导航网格权重 动作的曲线与函数 执行动作,根据动作完成度返回参数。 函数,在代码内执行同名函数即可调用。在执行关键帧时调用。 创建遮罩 绿色为可效用位置 将其运用到Animator上的遮罩,可…...

基于bearpi的智能小车--Qt上位机设计
基于bearpi的智能小车--Qt上位机设计 前言一、界面原型1.主界面2.网络配置子窗口模块二、设计步骤1.界面原型设计2.控件添加信号槽3.源码解析3.1.网络链接核心代码3.2.网络设置子界面3.3.小车控制核心代码总结前言 最近入手了两块小熊派开发板,借智能小车案例,进行鸿蒙设备学…...
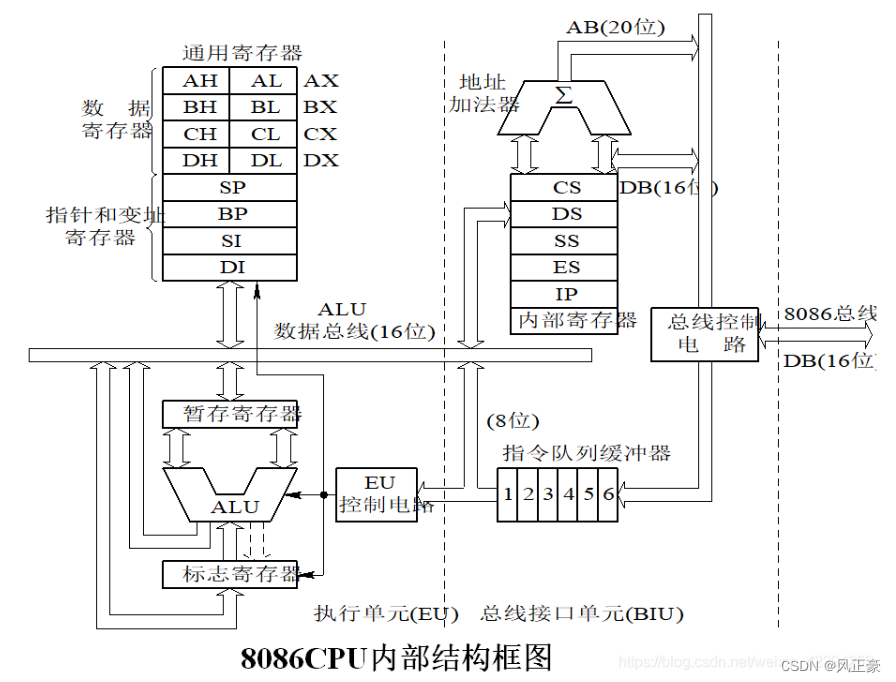
汇编语言与微机原理(1)基础知识
前言(1)本人使用的是王爽老师的汇编语言第四版和学校发的微机原理教材配合学习。(2)推荐视频教程通俗易懂的汇编语言(王爽老师的书);贺老师C站账号网址;(3)文…...

ASEMI代理瑞萨TW8825-LA1-CR汽车芯片
编辑-Z TW8825-LA1-CR在单个封装中集成了创建多用途车载LCD显示系统所需的许多功能。它集成了高质量的2D梳状NTSC/PAL/SECAM视频解码器、三重高速RGB ADC、高质量缩放器、多功能OSD和高性能MCU。TW8825-LA1-CR其图像视频处理能力包括任意缩放、全景缩放、图像镜像、图像调整和…...

什么是 .com 域名?含义和用途又是什么?
随着网络的发展,网络上出现了各种不同后缀的域名,这些域名的后缀各有不同的含义,也有不同的用途。今天,我们就一起来探讨一下 .com 后缀的域名知识。 .com 域名是一种最常见的顶级域名,它是由美国国家网络信息中心&…...
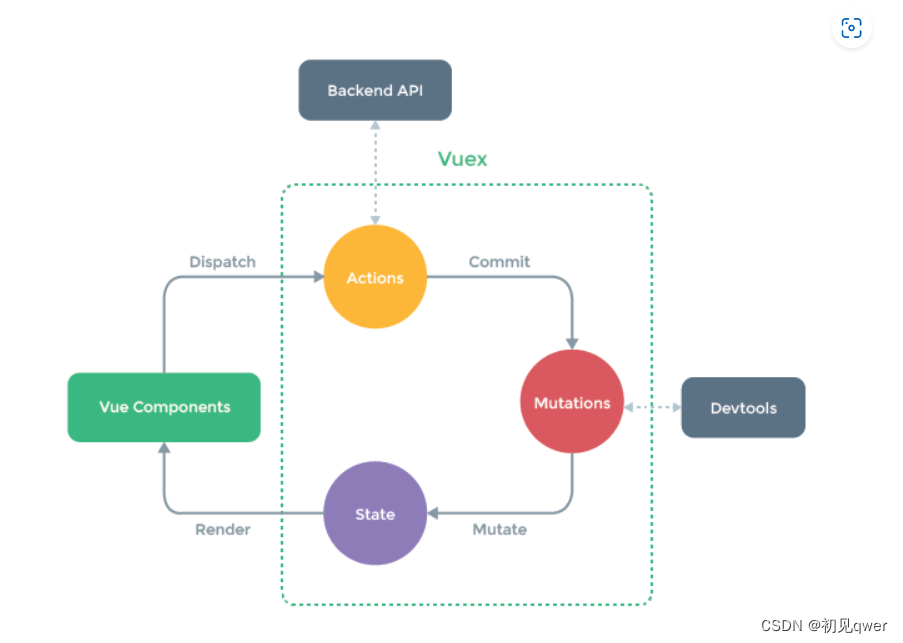
VueX快速入门(适合后端,无脑入门!!!)
文章目录前言State和Mutations基础简化gettersMutationsActions(异步)Module总结前言 作为一个没啥前端基础(就是那种跳过js直接学vue的那种。。。)的后端选手。按照自己的思路总结了一下对VueX的理解。大佬勿喷qAq。 首先我们需要…...
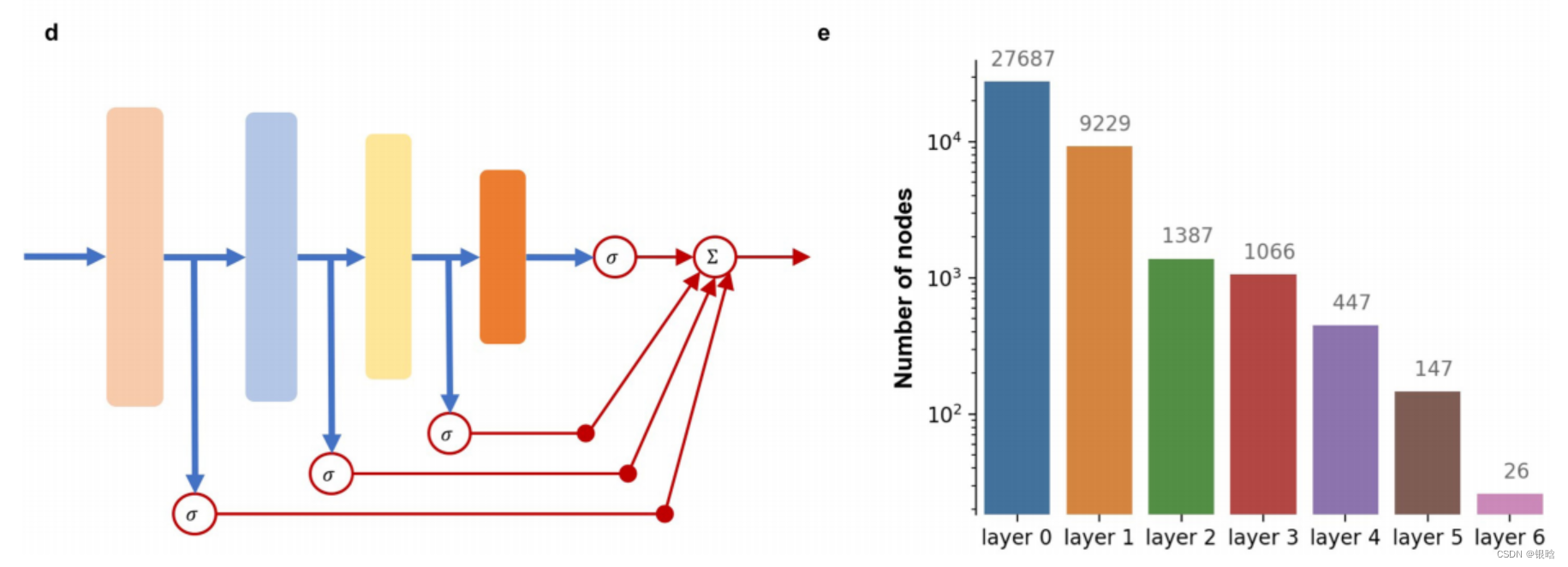
前列腺癌论文笔记
名词解释 MRF: 磁共振指纹打印技术( MR Fingerprinting)是近几年发展起来的最新磁共振技术,以一种全新的方法对数据进行采集、后处理和实现可视化。 MRF使用一种伪随机采集方法,取代了过去为获得个体感兴趣的参数特征而使用重复系列数据的采集方法&…...

Python+Yolov5道路障碍物识别
PythonYolov5道路障碍物识别如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助!前言这篇博客针对<<PythonYolov5道路障碍物识别>>编写代码,代码整洁,规则,易读。 学习与…...
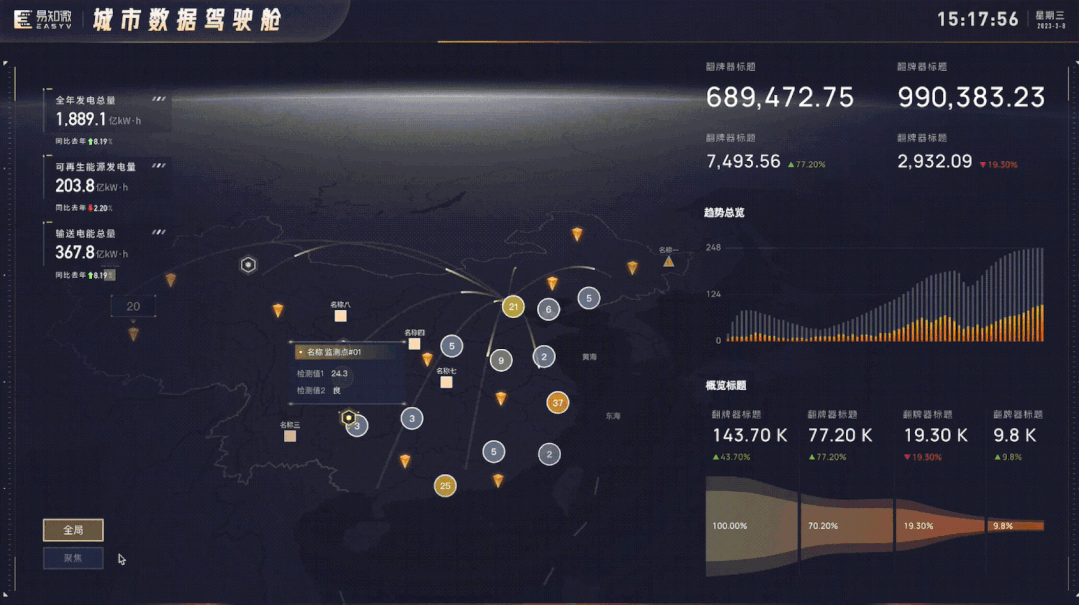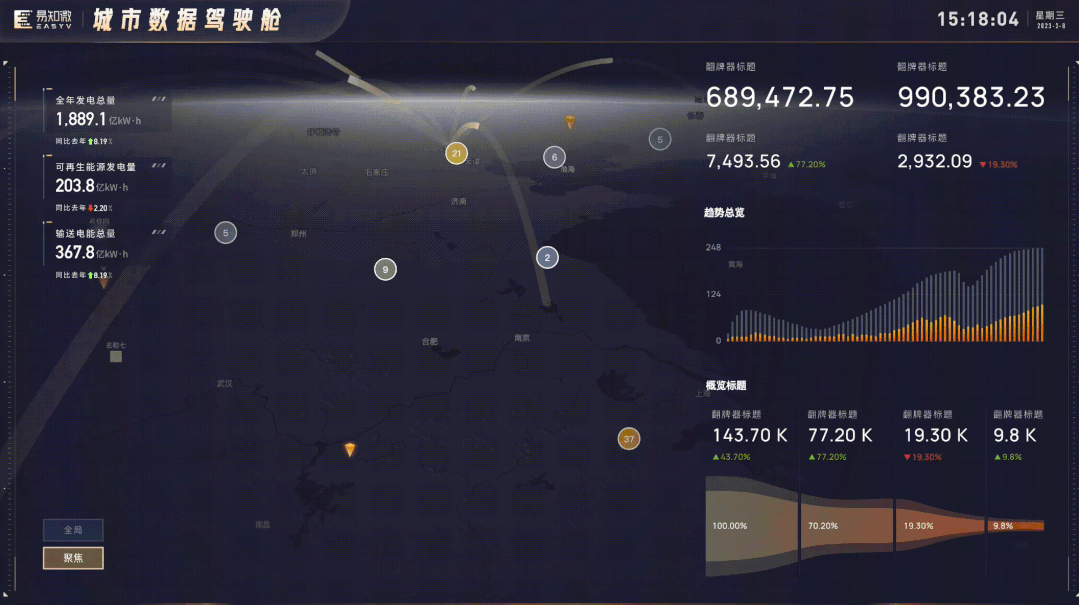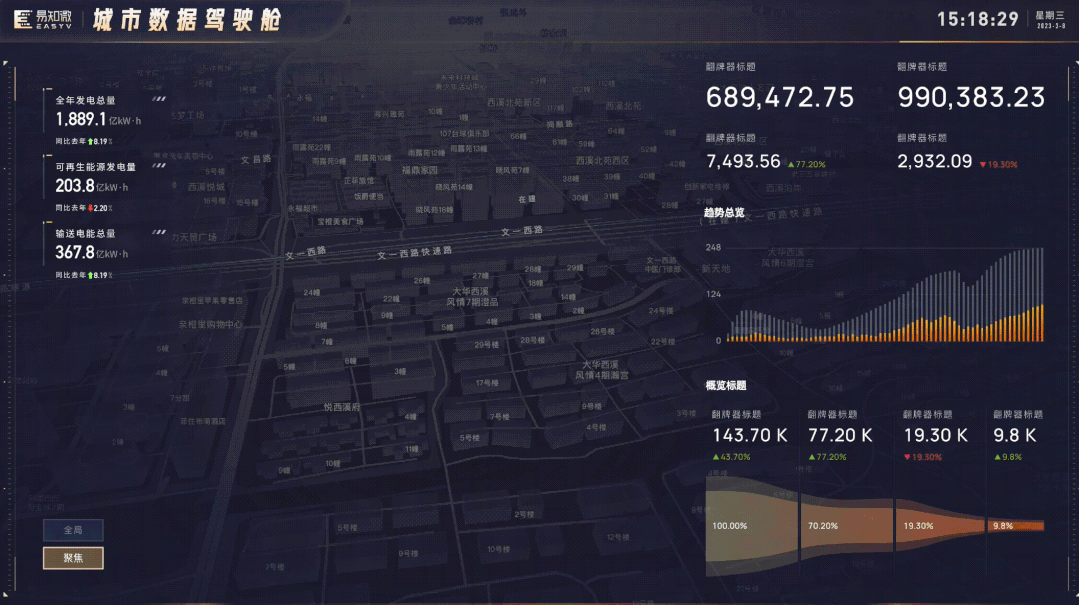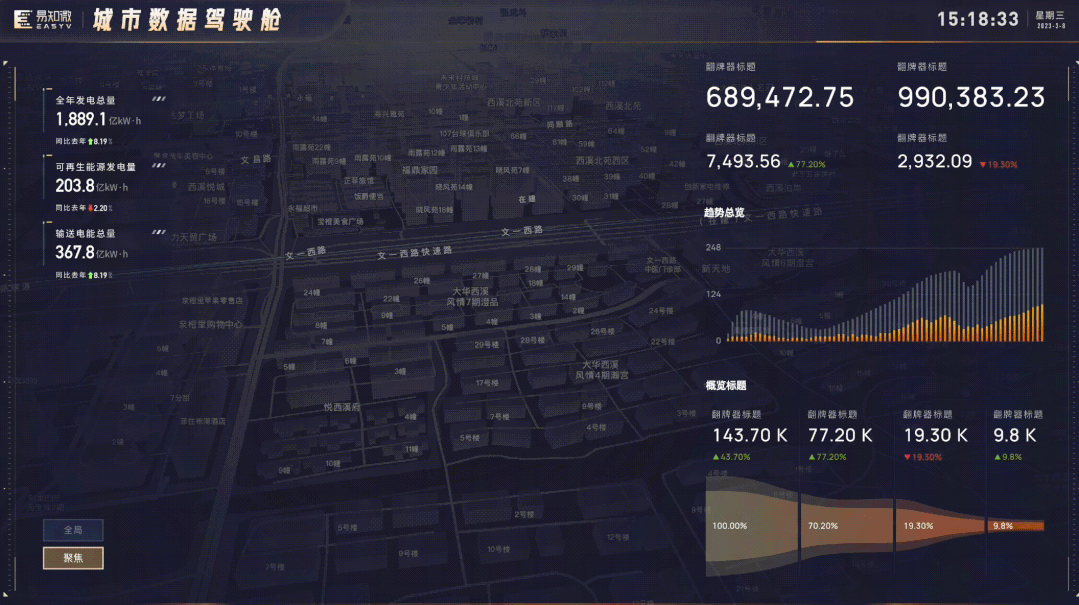
全新升级,EasyV 3D高德地图组件全新上线
当我们打开任意一个可视化搭建工具或者搜索数据可视化等关键词,我们会发现「地图」是可视化领域中非常重要的一种形式,对于许多可视化应用场景都具有非常重要的意义,那对于EasyV,地图又意味着什么呢?EasyV作为数字孪生…...
从管理到变革,优秀管理者的进阶之路
作为一位管理者,了解自身需求、企业需求和用户需求是非常重要的。然而,仅仅满足这些需求是不够的。我们还需要进行系统化的思考,以了解我们可以为他人提供什么价值,以及在企业中扮演什么样的角色。只有清晰的自我定位,…...

安装Anaconda3
安装Anaconda3 下载安装文件 可以去官网下载 https://repo.anaconda.com/archive/根据自己的操作系统选择合适的Anaconda版本 我选择的是Anaconda3-2021.05-Linux-x86_64.sh的版本 方法一:可以下载到本地然后在上传到虚拟机 方法二:在终端输入以下…...
HTTPS,SSL(对称加密和非对称加密详解)
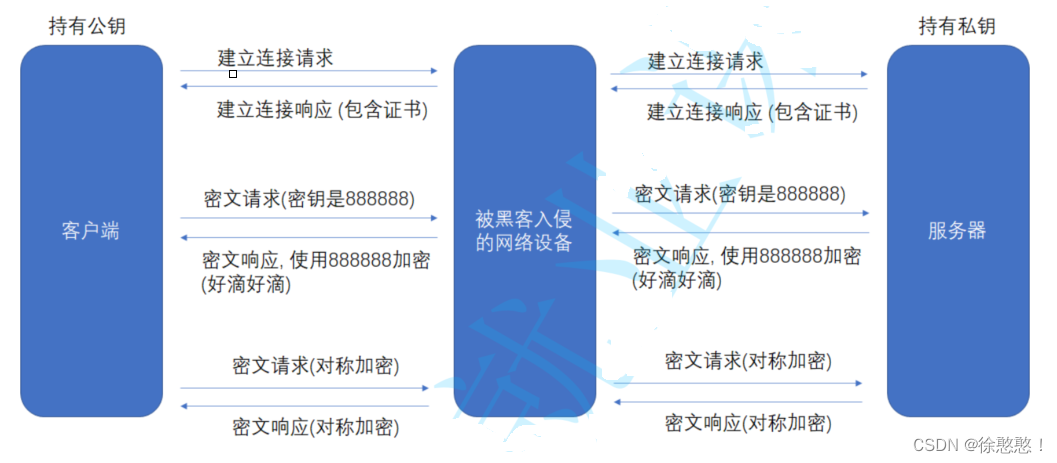
上一篇博客(HTTP详解_徐憨憨!的博客-CSDN博客)详细讲解了关于HTTP的知识,了解到HTTP协议下的数据传输是一种明文传输,既然是明文传输,可能导致在传输过程中出现一些被篡改的情况,此时就需要对所…...

【数据结构】还不懂算法复杂度?一文带你速解
前言:前面我们已经系统的学完C语言的相关知识,现在我们已经较为熟练的掌握了C语言中的各中代码语法和结构使用,能够使用代码来解决一些简单问题。但是对于一个程序员来说,仅仅会语法是远远不够的,从今天开始,我们将进入…...
案例描述:update中,MySQL inner join 和 left join的区别,小结果集驱动大结果集
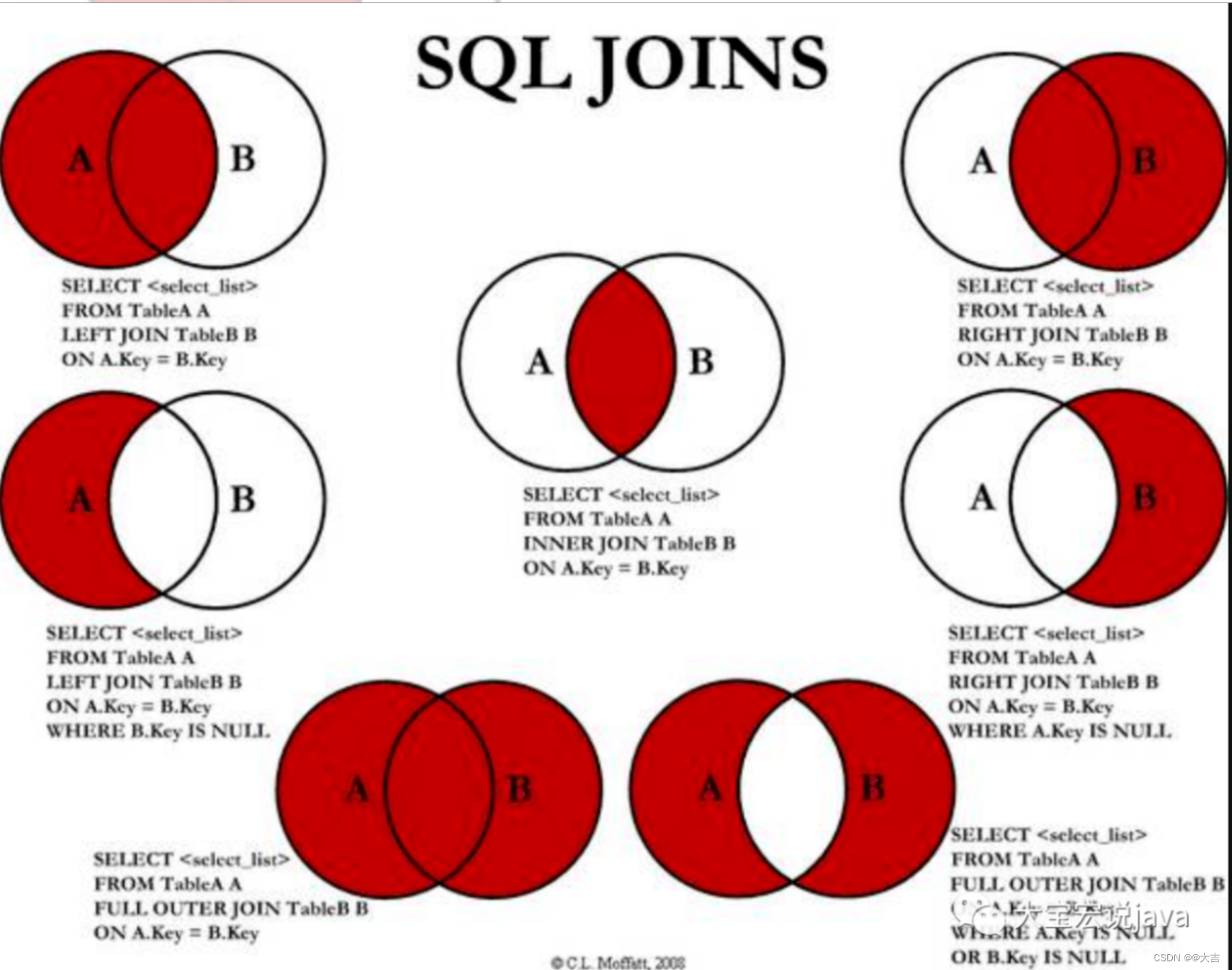
场景描述 以一个场景为例: 单据A:下游子表 (数据量级小) 单据B:下游主表(数据量级小) 单据C:中游子表(数据量级小) 单据D:中游主表(…...

CF1784D Wooden Spoon
CF1784D Wooden Spoon 题目大意 有2n2^n2n个人,进行nnn轮比赛。比赛的图是一棵完全二叉树。编号小的人一定能赢编号大的人,如果一个人满足: 第一次比赛被打败打败这个人的人在第二次比赛中被打败打败上一个人的人在第三次比赛中被打败…\d…...
【数据结构】栈
文章目录😺前言栈初始化栈顶入栈栈顶出栈栈体判空栈的数据个数获取栈顶元素栈的销毁整体代码😼写在最后😺前言 👻前面我们学习了链表,总算是跨过一个台阶了,本章带大家轻松一波,领悟一下栈的魅力…...
C++单继承和多继承
C单继承和多继承继承单继承写法继承中构造函数的写法写法构造和析构的顺序问题多继承继承 1.继承,主要是遗传学中的继承概念 2.继承的写法,继承中的权限问题 3.继承中的构造函数的写法 继承:子类没有新的属性,或者行为的产生 父类…...
金三银四,今年企业招聘如何?
又是一年求职季,互联网人找工作,和找对象一样严谨,不随便放手更不随便牵手。于是挑挑拣拣,最后的结果可能就是把自己挑剩下了。 时间已经悄然滑进3月中旬,多少无处安放的青春,还没尘埃落定?优秀…...

数字信号处理:滤波、频谱
一、滤波算法 应该说数字滤波器可以有效减小50Hz工频的干扰,完全消除是不可能的。以20ms为最小单位的整倍数周期滤波,可以有效减少工频的干扰。 软件中构建 IIR 陷波或者 FIR 带阻 数字滤波器,消除工频干扰对测量结果的影响。 1. 自适应滤波 …...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
