【数据结构】AVL树(平衡二叉搜索树)
文章目录
- 1.AVL树
- 1.1 AVL树的概念
- 1.2 AVL树节点的定义
- 1.3 AVL树的插入
- 1.4 AVL树的旋转
- 1.4.1 左单旋
- 1.4.2 右单旋
- 1.4.3 右左双旋
- 1.4.4 左右双旋
- 1.5 AVL树的平衡验证
- 1.6 AVL树的删除
- 1.7 AVL树的性能

1.AVL树
在前面,我们已经介绍过了二叉搜索树,也了解到二叉搜索树查找的效率非常的高。但是在数据有序或接近有序时,它就会退化成单边树,那样效率就变得非常低了。所以我们也一直说二叉搜索树的搜索的时间复杂度是O(N)(高度次),并不是O(log2N)。

因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
1.1 AVL树的概念
由于二叉搜索树可能会退化,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
为什么要求左右子树的高度之差不超过1就可以呢?
对于所有形状的子树来说,如果他有2n-1个节点,那它就可以保持绝对的平衡;如果他有2n (n >= 1)个节点,就无法做到绝对的平衡,最好的结果就是子树高度相差一。
一棵AVL树要么是空树,要么是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果他有n个节点,其高度可保持在log2N,搜索的时间复杂度就是log2N。
1.2 AVL树节点的定义
为了方便确认一棵树是否是AVL树,我们在节点中定义一个平衡因子,通过它来记录每棵树左右子树的高度。
如果右子树比左子树高一层,那平衡因子就是1;如果左右子树一样高,那平衡因子就是0;如果左子树比右子树高一层,那平衡因子就是-1。此时AVL树的性质都没有被打破。
当左子树比右子树高两层,那平衡因子就是-2;或者右子树比左子树高两层,平衡因子就是2,此时AAVL树的性质就被打破了,需要调整。
在调整失衡的AVL树时,我们需要频繁的访问其父节点,因此我们给每个节点定义一个指向父亲的指针
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv; //存放数据AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _prev; //指向当前节点的父亲int _bf;//平衡因子AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),prev(nullptr),_bf(0){}
};
1.3 AVL树的插入
AVL树的插入与普通二叉搜索树的插入基本一致。唯一的区别就是AVL树插入节点后需要判断AVL树是否失衡,存在失衡就需要调整。
我们平衡因子是使用右子树的高度-左子树的高度,因此,如果新节点插入到父节点的右边,那父亲的平衡因子+1;如果新节点插入到父亲节点的左边,那父亲的平衡因子-1。

对于情况二来说,新节点的插入不会影响其祖先的平衡因子的改变,因为子树的高度没有改变。
对于情况一来说,新节点的插入会影响其祖先的平衡因子的改变,因为子树的高度变高了。

所以,对于情况一来说,我们新插入节点后,还要观察其祖先的平衡因子是否变化,变化后是否需要调整。
那么下面我们就先将节点插入到树中:
bool insert(const pair<K, V>& kv){//插入前是空树if (_root == nullptr){//新插入的节点就是根_root = new Node(kv);_root->_prev = nullptr;return true;}else{Node* cur = _root;Node* parent = nullptr;//寻找插入位置while (cur){if (cur->_kv.first < kv.first){parent = cur;//记录父节点,以便后序连接cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;//节点已经存在,插入失败}}//已找到了插入位置cur = new Node(kv);//判断连接在父亲的哪一侧if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;cur->_prev = parent;//指向父亲//判断树是否失衡//...}}
更新父亲/祖先的平衡因子
//判断树是否失衡while (parent){//更新父亲的平衡因子if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)//属于情况二,不影响祖先break;//情况一,影响祖先的平衡因子,需要继续更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_prev;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转处理break;}else{assert(false);//平衡因子异常了}}
1.4 AVL树的旋转
AVL树的旋转分为四种情况:
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
下面,我们对这四种情况具体分析
1.4.1 左单旋
新节点插入到较高右子树的右侧- -左单旋

在旋转过程中,有以下几种情况需要考虑:
- 7节点的左孩子可能存在,也可能不存在
- 6可能是根节点,也可能是子树
- 如果是根节点,旋转完成后,根节点就是7
- 如果是子树,可能是某个节点的左子树,也可能是右子树,需要判断以后连接
void RotateL(Node* parent){Node* subR = parent->_right;//父亲的右孩子Node* subRL = subR->_left;//右孩子的左孩子//升高度,连孙子parent->_right = subRL;if (subRL)subRL->_prev = parent;Node* parentPrev = parent->_prev;//降高度,变父亲subR->_left = parent;parent->_prev = subR;//连接旋转后的子树subR->_prev = parentPrev;if (parentPrev == nullptr){//如果原父亲就是根,旋转后的儿子变根_root = subR;}else{//原父亲是子树,判断儿子连接在哪一边if (parentPrev->_left == parent)parentPrev->_left = subR;elseparentPrev->_right = subR;}//更新平衡因子subR->_bf = 0;parent->_bf = 0;}
1.4.2 右单旋
新节点插入到较高左子树的左侧- - 右旋

在旋转过程中,有以下几种情况需要考虑:
- 5节点的右孩子可能存在,也可能不存在
- 6可能是根节点,也可能是子树
- 如果是根节点,旋转完成后,根节点就是5
- 如果是子树,可能是某个节点的左子树,也可能是右子树,需要判断以后连接
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//升高度,连孙子parent->_left = subLR;if (subLR)subLR->_prev = parent;Node* parentPrev = parent->_prev;//降高度,变父亲subL->_right = parent;parent->_prev = subL;//新父亲指向前subL->_prev = parentPrev;if (nullptr == parentPrev){//如果原父亲就是根,旋转后的儿子变根_root = subL;}else{//原父亲是子树,判断儿子连接在哪一边if (parentPrev->_left == parent)parentPrev->_left = subL;elseparentPrev->_right = subL;}subL->_bf = 0;parent->_bf = 0;}
1.4.3 右左双旋
新节点插入到较高右子树的左侧- -右左双旋

所以,为了解决这种情况,我们可以将这种歪脖树先变成一棵单边树,然后再进行单旋即可。

为了满足所有情况,我们下面使用抽象图再画一遍


观察上图我们可以发现,双旋就是一种抛弃自己的孩子,独自登基的感觉,因此对于旋转后平衡因子的改变,取决于新节点插入到哪一边,最后又到哪里去。
void RotateRL(Node* parent){//由于单旋会改变节点的位置以及平衡因子,所以提前记录Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//修改平衡因子if (bf == 0)//subRL插入前是空{parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1)//subRL之前是一棵树,新节点插入其 右侧{parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else //subRL之前是一棵树,新节点插入其 左侧{parent->_bf = 0;subR->_bf = -1;subRL->_bf = 0;}}

1.4.4 左右双旋
新节点插入到较高左子树的右侧–左右双旋
最简单的情况,2的右子树插入前为空

抽象图

跟右左双旋基本一样,这里就不赘述了,咱们直接开旋。

平衡因子的改变也需要小心。
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0) // subLR插入前为空{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1) //subLR是一棵树,新节点插入到树的 右侧{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else //subLR是一棵树,新节点插入到树的 左侧{parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}}

下面就是更新平衡因子的整体思路:
//判断树是否失衡while (parent){//更新父亲的平衡因子if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)//属于情况二,不影响祖先break;//情况一,影响祖先的平衡因子,需要继续更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_prev;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转处理//左单旋// p cur// cur ---> p new// newif (parent->_bf == 2 && cur->_bf == 1)RotateL(parent);//右单旋// p cur// cur ---> new p// newelse if (parent->_bf == -2 && cur->_bf == -1)RotateR(parent);//右左双旋// p p cur// cur --> cur --> p new// new newelse if (parent->_bf == 2 && cur->_bf == -1)RotateRL(parent);//左右双旋// p p cur// cur --> cur --> new p // new newelse if (parent->_bf == -2 && cur->_bf == 1)RotateLR(parent);elseassert(false);break;//旋转后,以parent为根的树已经平衡,无需继续向上更新}else{assert(false);//平衡因子异常了}
总结:
假如以Parent为根的子树不平衡,即Parent的平衡因子为2或者-2,分以下情况考虑
- Parent的平衡因子为2,说明Parent的右子树高,设Parent的右子树的根为SubR
- 当SubR的平衡因子为1时,执行左单旋
- 当SubR的平衡因子为-1时,执行右左双旋
- Parent的平衡因子为-2,说明Parent的左子树高,设Parent的左子树的根为SubL
- 当SubL的平衡因子为-1是,执行右单旋
- 当SubL的平衡因子为1时,执行左右双旋
旋转完成后,原Parent为根的子树个高度降低,已经平衡,不需要再向上更新。
1.5 AVL树的平衡验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
- 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
- 验证其为平衡树
- 每个节点子树高度差的绝对值不能超过1
- 节点的平衡因子是否计算正确
int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _isBalanceTree(){return isBalanceTree(_root);}bool isBalanceTree(Node* root){if (root == nullptr)//空树也是平衡二叉搜索树return true;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);int gap = rightHeight - leftHeight; //计算root的平衡因子// 如果计算出的平衡因子与root的平衡因子不相等,或者//root平衡因子的绝对值超过1,则一定不是AVL树if (gap != root->_bf || (gap > 1 || gap < -1)){return false;}return isBalanceTree(root->_left) && isBalanceTree(root->_right);}

1.6 AVL树的删除
- 因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除
- (分析有无左右孩子,若仅有一个孩子,则直接将删除节点连接孩子;若有两个孩子,将删除节点替换为删除节点的左子树的最大或右子树的最小)
- 然后再更新平衡因子,只不过与插入不同的是,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
1.7 AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log2N。
但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。

相关文章:

【数据结构】AVL树(平衡二叉搜索树)
文章目录 1.AVL树1.1 AVL树的概念1.2 AVL树节点的定义1.3 AVL树的插入1.4 AVL树的旋转1.4.1 左单旋1.4.2 右单旋1.4.3 右左双旋1.4.4 左右双旋 1.5 AVL树的平衡验证1.6 AVL树的删除1.7 AVL树的性能 1.AVL树 在前面,我们已经介绍过了二叉搜索树,也了解到…...

ASP.NET Web Api 使用 EF 6,DateTime 字段如何取数据库服务器当前时间
前言 在做数据库设计时,为了方便进行数据追踪,通常会有几个字段是每个表都有的,比如创建时间、创建人、更新时间、更新人、备注等,在存储这些时间时,要么存储 WEB 服务器的时间,要么存储数据库服务器的时间…...

【HarmonyOS】应用设置屏幕常亮
【HarmonyOS】应用设置屏幕常亮 一、问题背景: 金融类或钱包场景的应用APP,对于付款码,扫一扫等场景都会对屏幕设置常亮。防止屏幕长时间不操作,自动息屏。 目前这种场景的需求也是非常有必要的,也是行业内默认的处理…...

Docker部署Elasticsearch8.6.0 Kibana8.6.0
(1)Docker部署Elasticsearch8.5.3(失败…) 为了匹配springboot3.0.x,安装Elasticsearch:8.5.3 拉取镜像,遇到问题! [rootserver01 ~]# docker pull elasticsearch:8.5.3 8.5.3: Pulling from…...

第四篇论文小记
一、第一次投稿 期刊:《Remote Sensing》 研究方向:人工智能应用 投稿结果:已投被拒 投稿周期:3天 最后更新时间:19 July 2024 投稿流程: 状态时间Pending review16 July 2024Reject by editor19 July …...

python使用 tkinter 生成随机颜色
先看效果: 只要不停点击底部的按钮,每次都会生成新的颜色。炫酷啊。 import random import tkinter import tkinter.messagebox from tkinter import Button# todo """ 1. 设置一个按钮,来让用户选择是否显示颜色值 2. 把按钮换成 Label…...

【Linux学习 | 第1篇】Linux介绍+安装
文章目录 Linux1. Linux简介1.1 不同操作系统1.2 Linux系统版本 2. Linux安装2.1 安装方式2.2 网卡设置2.3 安装SSH连接工具2.4 Linux和Windows目录结构对比 Linux 1. Linux简介 1.1 不同操作系统 桌面操作系统 Windows (用户数量最多)MacOS ( 操作体验好,办公人…...
设计模式-抽象工厂
抽象工厂属于创建型模式。 抽象工厂和工厂设计模式的区别: 工厂模式的是设计模式中最简单的一种设计模式,主要设计思想是,分离对象的创建和使用,在Java中,如果需要使用一个对象时,需要new Class()ÿ…...

Ubunton-24.04 简单配置使用
目录 1.设置 root 密码 2. 防火墙设置 1. 安装防火墙 2. 开启和关闭防火墙 3. 开放端口和服务规则 4. 关闭端口和删除服务规则 5 查看防火墙状态 3. 设置网络 1.设置 root 密码 1. 切换到 root 用户,并输入当前登录账号的密码 sudo -i 2. 设置新密码…...
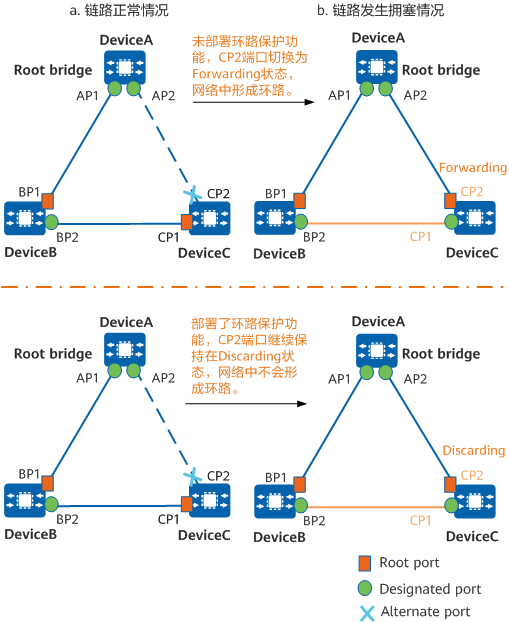
什么是STP环路保护
在运行生成树协议的网络中,根端口和其他阻塞端口状态是依靠不断接收来自上游设备的BPDU维持。当由于链路拥塞或者单向链路故障导致这些端口收不到来自上游交换设备的BPDU时,设备会重新选择根端口。原先的根端口会转变为指定端口,而原先的阻塞…...

Python算法基础:解锁冒泡排序与选择排序的奥秘
在数据处理和算法设计中,排序是一项基础且重要的操作。本文将介绍两种经典的排序算法:冒泡排序(Bubble Sort)和选择排序(Selection Sort)。我们将通过示例代码来演示这两种算法如何对列表进行升序排列。 一…...

QtCMake工程提升类后找不到头文件
链接: QtCMake工程提升类后找不到头文件_qt提升类找不到头文件-CSDN博客 重点: 1.原因:出现问题的原因是Qt creator通过ui文件生成的程序和存放头文件的目录不在一起,但是生成的程序里会在生成目录下找头文件,所以肯…...

Docker核心技术:Docker原理之Cgroups
云原生学习路线导航页(持续更新中) 本文是 Docker核心技术 系列文章:Docker原理之Cgroups,其他文章快捷链接如下: 应用架构演进容器技术要解决哪些问题Docker的基本使用Docker是如何实现的 Docker核心技术:…...

union的特性和大小端
一、union在c和c语言中的特性 1.共享内存空间:union的所有成员共享同一块内存空间。意味着在同一时刻,union 只能存储其成员 中的一个值。当你修改了union中的一个成员,那么其它成员的值也会被改变,因为它们实际上都是指向同一块…...

个性化IT服务探索实践
探索和实践个性化IT服务,可以为用户提供更优质、定制化的解决方案,从而提升用户体验和满意度。以下是一些具体的步骤和建议,帮助自己在未来探索和实践个性化IT服务。 一、了解用户需求 用户调研和反馈: 进行用户调研,了解用户的需求和痛点。收集用户反馈,通过问卷、采访…...

UE4-打包游戏,游戏模式,默认关卡
一.打包游戏 注意windows系统无法打包苹果系统的执行包,只能使用苹果系统打包。 打包完之后是一个.exe文件。 打包要点: 1.确定好要操控的角色和生成位置。 2.设置默认加载的关卡和游戏模式。 在这个界面可以配置游戏的默认地图和游戏的模式,…...

Unity ShaderLab基础
[原文1] [参考2] 一 基础知识 1. 1 着色器语言分类: 语言说明HLSL基于 OpenGL 的 OpenGL Shading LanguageGLSL基于 DirectX 的 High Level Shading LanguageCGNVIDIA 公司的 C for GraphicShader LabUnity封装了CG,HLSL,GLSL的Unity专用着色器语言,具有跨平台,图形化编程,便…...

用代理IP会频繁掉线是什么原因?HTTP和SOCKS5协议优劣势是什么?
在使用代理IP的过程中,频繁掉线是一个常见且令人头痛的问题。要解决这一问题,我们需要先了解其原因,然后比较HTTP和SOCKS5两种代理协议的优劣势,以选择最适合的解决方案。 一、代理IP频繁掉线的原因 1. 代理服务器稳定性 代理服…...

MongoDB教程(十三):MongoDB覆盖索引
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 文章目录 引言什么是覆盖…...

快速认识EA(Enterprise Architecture)
前言 企业架构,英文是:Enterprise Architecture,简称:EA,是承接企业战略规划与IT建设之间的桥梁,是企业信息化的核心,主要包括业务架构和IT架构。 架构的本质是管理和解决系统的复杂性&#x…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
