【网络流】——初识(最大流)
网络流-最大流
- 基础信息
- 引入
- 一些概念
- 基本性质
- 最大流
- 定义
- Ford–Fulkerson 增广
- Edmons−Karp算法
- Dinic 算法
- 参考文献
基础信息
引入
假定现在有一个无限放水的自来水厂和一个无限收水的小区,他们之间有多条水管和一些节点构成。
每一条水管有三个属性:流向,流量,容量。我们用 ( u , v ) (u,v) (u,v) 表示一条水管,这意味着水管中的水只能从 u u u 流向 v v v,而不能从 v v v 流向 u u u。流量即经过这条水管的单位时间内经过这条水管的水量。
我们将其模型化成为一个有向图,如下图所示,边上的数字即为水管的容量,流向用箭头来表示。当然,现在所有的水管流量都是 0 0 0。

对于这一类型的有向图,我们称之为流网络。
一些概念
对于一个流网络,我们有如下几个概念:
- 源点:发送流的节点。
- 汇点:接收流的节点。
- 弧:流网络图中的有向边,为了方便,后文均用“边或弧”表示
- 弧的流量:在一个流网络中,每一条边都有一个流量,即单位时间内流经该边的流的量。一般地,我们使用流量函数 f ( x , y ) f(x,y) f(x,y) 表示 ( x , y ) (x,y) (x,y) 的流量。
- 弧的容量:在一个流网络中,每一条边都会有一个容量限制,即边上流量的最大值。一般地,我们使用容量函数 c ( x , y ) c(x,y) c(x,y) 表示 ( x , y ) (x,y) (x,y) 的容量。
- 弧的残量:即每一条边的剩余容量,可以表示为 c ( x , y ) − f ( x , y ) c(x,y)-f(x,y) c(x,y)−f(x,y),用 c f ( u , v ) c_f(u,v) cf(u,v) 表示
- 容量网络:已知每一条边的容量的流网络即为容量网络
- 流量网络:已知每一条边的流量的流网络即为流量网络
- 残量网络:已知每一条边的残量的流网络即为残量网络。所有边的流量均为 0 0 0 的残量网络就是容量网络。用 G f G_f Gf 表示,即 G f = ( V , E f ) , E f = G_f=(V,E_f),E_f= Gf=(V,Ef),Ef={ ( u , v ) ∣ c f ( u , v ) > 0 (u,v)|c_f(u,v)>0 (u,v)∣cf(u,v)>0 }
请确保你对概念比较熟悉
基本性质
- 容量限制: ∀ ( x , y ) ∈ E , 0 ≤ f ( x , y ) ≤ c ( x , y ) \forall (x,y)\in E,0\le f(x,y)\le c(x,y) ∀(x,y)∈E,0≤f(x,y)≤c(x,y)
- 斜对称性: ∀ ( x , y ) ∈ E , f ( x , y ) = − f ( y , x ) \forall (x,y)\in E,f(x,y)=-f(y,x) ∀(x,y)∈E,f(x,y)=−f(y,x)
- 流量守恒:除了源点与汇点之外,流入任何节点的流一定等于流出该节点的流。
最大流
定义

通俗地讲,回到引例,现在有一个问题需要我们去解决:水厂在单位时间内最多能发送多少水给小区?
这就是网络流中的一个问题:最大流问题。

Ford–Fulkerson 增广
- 假设有源点到汇点的一条可行路径 R R R,满足 ∀ ( x , y ) ∈ R , c f ( x , y ) > 0 \forall(x,y)∈R,c_f(x,y)>0 ∀(x,y)∈R,cf(x,y)>0,即残量为严格大于 0 0 0,我们称 R R R 为一条增广路。
- 此时我们可以得出一个简单的思路:在残量网络中不断地寻找增广路,从源点向汇点发送流。该增广路的流量满足 0 < f ≤ m i n ( c f ( x , y ) ) 0<f\le min(c_f(x,y)) 0<f≤min(cf(x,y)),为了取得最大流,我们自然而然的令该增广路的流量为 min ( c f ( x , y ) ) \min(c_f(x,y)) min(cf(x,y)),然后修改路径上每一条边的残量即可。
- 这个思路即为Ford−Fulkerson方法,简称为FF方法。
- 可以使用DFS实现基本的Ford−Fulkerson算法。
- 为了保证算法的正确性,有时候我们需要缩减流网络中一些特定边的流量。
- 举个例子,如图。
假定我们使用DFS找到了红色的这一条增广路径,显然此时源点到汇点的流量为1。此时图中不再有任何增广路径,但是这个流是最大流吗?

显然不是,我们可以找到更好的,如图:

此时流量为 2 2 2,这才是最大流。
- 问题出在哪里?
- 由于我们没有给程序一个反悔的机会,所以才会出现上面这样的尴尬情况。
- 那么如何解决这个问题呢?
- 引入“后向弧”。我们给每一条边 ( u , v ) (u,v) (u,v) 建立一条对应的反向边 ( v , u ) (v,u) (v,u),用于对正向边流量的缩减。
- 很自然地,我们会把反向边的初始残量设置为 0 0 0,因为没有正向流量,无法缩减。
- 那么观察下面的算法图示:

然后对于初学者可能会注意到:反向边的流量 f ( v , u ) f(v,u) f(v,u) 可能是一个负的,这里可以参考一下 OI-WIKI 的解释。


是不是有点懵?
- 通俗的文字解释就是:反向边的功能是将正向边的流量往回推送,此时反向边推送的流量(反向流量)最多恰好把正向流量抵消,所以反向边的残量等于正向边流量。
- 综上所述,反向边的残量应当是动态更新,一旦正向边的流量更新,反向边的残量也需要更新。
Edmons−Karp算法
观察到基于 DFS 的FF 可能不是很优。
- 观察这样一张图,如果我们使用基于DFS实现的FF方法,假定一开始找到的增广路径为红色的这一条,那么我们可能需要反复进行 999 × 2 999\times 2 999×2次DFS才能够找到最大流。

- 但是事实上,我们在最好情况下只需要走两次(直接走 999 999 999 的边)就能够达到最大流。
- 在这种情况下,我们引入EK算法。其基础仍然是FF方法,但是我们不再使用DFS,而是转为使用BFS寻找最短增广路改进效率,时间复杂度为 O ( n m 2 ) O(nm^2) O(nm2)。
参考代码:
queue<int> que;flow[s]=0x3f3f3f3f;que.push(s);
for (int i=1;i<=n;i++)prep[i]=-1,pree[i]=0;
prep[s]=0;
while(!que.empty())
{int now=que.front();que.pop();for (int i=head[now];i;i=e[i].next){if(e[i].val>0&&prep[e[i].to]==-1){flow[e[i].to]=min(flow[now],e[i].val);//flow记录的是在增广路上经过该点的流量pree[e[i].to]=i;//用于记录前驱边的编号prep[e[i].to]=now;//用于记录前驱节点if (e[i].to==t) break;que.push(e[i].to);}}
}
if (prep[t]!=-1) return flow[t];
else return -1;
- 下一步就是对路径上的所有边进行信息的更新。
- 现在有一个问题,我们如何快速取得反向边呢?
- 对于链式前向星,我们设置第一条边的编号为 2 2 2 ,我们存入一条正向边时,下一条边就存入反向边,那么只要对一条边的编号异或 1 1 1 就能取得它对应的反向边。
- 证明:偶数的二进制表示最后一位为 0 0 0 ,对这个偶数异或 1 1 1 相当于对这个偶数 + 1 +1 +1。奇数的二进制表示最后一位为 1 1 1,对这个奇数异或 1 1 1 相当于对这个奇数 − 1 -1 −1。
那么路径的信息更新就可以轻松实现了。

Dinic 算法
- 由于EK算法每次只求一条最短增广路,其效率在某些情况下可能不够优秀。
- 对于下面这一张图,如果我们使用EK算法,那么我们至少需要重复三次EK算法的流程才能求出最大流。

- 自然而然地,我们会想到能不能实现多路增广呢?
于是 Dinic 算法就出来了。(其实就是把EK和FF融在一起)
Dinic算法的流程如下:
- BFS对流网络分层。
- DFS对图上增广路的信息进行更新。

如图所示,此时已经完成了对于流网络的分层,点上的编号即为所在的层数。
这个时候我们从源点开始DFS,在最好情况下,我们能同时找到三条增广路,即标红色的三条。
- BFS对图分层的作用在于一次可以得到多条长度相同的最短增广路。
- 那么路径的信息应该如何更新呢?
- 每次从当前点出发,选用从当前点所在层到下一层的边,发送一定的流量,流量的大小取边残量和当前点从源点获取的剩余流中两者的最小值。
- 搜索完成后,即不再有流能够往后发送,或者能够抵达汇点。此时返回一个流量值,即这条增广路的流量(若不再有流能够往后发送,则返回的流量值为0),此时就能够对边和反向边的残量进行更新了。
- Dinic算法就完成了,其时间复杂度为 O ( n 2 m ) O(n^2 m) O(n2m)。
- 显然,这样的时间复杂度并算不上多么高效,原因在于尽管我们一次BFS找到了多条增广路,但是DFS时路径的信息仍然是一条一条更新的。
参考代码:
BFS实现:

实现难度不大,只是一个模板BFS。
dis数组用于记录层数,vis数组用于记录是否被访问过。
事实上vis数组是不必要的,因为dis数组也可以实现一样的功能。
DFS实现:

注意到,Dinic算法的复杂度上界也不是很优, 所以,我们会考虑对DFS的过程加入一定的优化。
当前弧优化:
- 在DFS的过程中,我们可能会多次经过一个点。我们会重复的处理一些边。
- 但是事实上,在每次处理的过程中,已经处理完毕的边在这次DFS中不再有任何作用,一旦处理完毕,该边的“潜力”一定已经被榨干了。
- 所以,我们每次只需要记录当前处理的边的编号,下次经过这个点的时候,可以直接从这条边开始。
- 这就叫作当前弧优化。
证明:增广次数为 O ( m ) O(m) O(m),每次增广最多经过 O ( n ) O(n) O(n) 个点,总复杂度为 O ( n m ) O(nm) O(nm)
注意,不写这个优化,复杂度是错的,可能退化为 O ( n m 2 ) O(nm^2) O(nm2)
点优化:
-
假如从一个点流不出流量,则把该点的dis变为 − 1 -1 −1,这样这一次多路增广再也不会来了。
-
大多数情况下这只能优化常数,但是在某些毒瘤题里面跑的很快。
这就是常用的两个优化,更多的可以参考 command_block大佬的博客。
虽然EK和Dinic的时间复杂度上界都不是非常优秀,但是在实际应用上效率非常高。
对于EK算法,一般能够解决 1 0 3 到 1 0 4 10^3 \text{到}10^4 103到104 的网络流问题。
对于Dinic算法,一般能够解决 1 0 4 到 1 0 5 10^4 \text{到}10^5 104到105 的网络流问题。
Dinic完整的参考代码:
#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
using namespace std;
const int N=1e5+1,inf=1e9;
struct fy{int v,w,nxt;
}e[N];
int head[N],idx=1,n,m,s,t,ans=0,dis[N],cur[N],vis[N];
void add(int x,int y,int z){e[++idx].v=y,e[idx].w=z,e[idx].nxt=head[x],head[x]=idx;
}
bool bfs(){for(int i=1;i<=n;i++)dis[i]=0,vis[i]=0,cur[i]=head[i];vis[s]=1,dis[s]=1;queue<int>Q;Q.push(s);while(!Q.empty()){int u=Q.front();Q.pop();for(int i=head[u];i;i=e[i].nxt){int v=e[i].v;if(!vis[v]&&e[i].w>0){dis[v]=dis[u]+1;vis[v]=1;if(v==t)return 1;Q.push(v);}}}return 0;}
int dfs(int u,int flow){if(!flow||u==t)return flow;int used=0;for(int i=cur[u];i;i=e[i].nxt){cur[u]=i;int v=e[i].v;if(dis[u]+1!=dis[v])continue;int _=dfs(v,min(flow-used,e[i].w));if(_){e[i].w-=_;e[i^1].w+=_;used+=_;if(flow-used==0)return flow;}}return used;
}
signed main(){IOS;cin>>n>>m>>s>>t;for(int i=1,x,y,z;i<=m;i++)cin>>x>>y>>z,add(x,y,z),add(y,x,0);while(bfs())ans+=dfs(s,inf);cout<<ans<<"\n";return 0;
}
当然,常用的是Dinic,但还有MPN算法,ISAP,Push-Relabel 预流推进算法 等其他方法,可能以后会填坑
参考文献
- OI-WIKI
- command_block的博客
相关文章:

【网络流】——初识(最大流)
网络流-最大流 基础信息引入一些概念基本性质 最大流定义 Ford–Fulkerson 增广Edmons−Karp算法Dinic 算法参考文献 基础信息 引入 假定现在有一个无限放水的自来水厂和一个无限收水的小区,他们之间有多条水管和一些节点构成。 每一条水管有三个属性:…...

【STM32嵌入式系统设计与开发---拓展】——1_10矩阵按键
这里写目录标题 1、矩阵按键2、代码片段分析 1、矩阵按键 通过将4x4矩阵按键的每一行依次设为低电平,同时保持其它行为高电平,然后读取所有列的电平状态,可以检测到哪个按键被按下。如果某列变为低电平,说明对应行和列的按键被按下…...

长期更新方法库推荐pmq-ui
# pmq-ui pmq-ui 好用方法库ui库, 欢迎您的使用 ## 安装 1. 克隆项目库到本地: 2. 进入项目目录:cd pmq-ui 3. 安装依赖:npm install pmq-ui ## 使用 <!-- 1. 启动应用: 2. 访问 [http://localhost:3000](http://localhost:300…...

<数据集>抽烟识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:4860张 标注数量(xml文件个数):4860 标注数量(txt文件个数):4860 标注类别数:1 标注类别名称:[smoking] 使用标注工具:labelImg 标注规则:对…...

SQL Server 端口设置教程
引言 你好,我是悦创。 在配置 SQL Server 的过程中,设置正确的端口非常关键,因为它影响到客户端如何连接到 SQL Server 实例。默认情况下,SQL Server 使用 TCP 端口 1433,但在多实例服务器上或出于安全考虑ÿ…...

【React1】React概述、基本使用、脚手架、JSX、组件
文章目录 1. React基础1.1 React 概述1.1.1 什么是React1.1.2 React 的特点声明式基于组件学习一次,随处使用1.2 React 的基本使用1.2.1 React的安装1.2.2 React的使用1.2.3 React常用方法说明React.createElement()ReactDOM.render()1.3 React 脚手架的使用1.3.1 React 脚手架…...

k8s部署kafka集群
k8s部署kafka集群 kafka(Kafka with KRaft) mkdir -p ~/kafka-ymlkubectl create ns kafkacat > ~/kafka-yml/kafka.yml << EOF apiVersion: v1 kind: Service metadata:name: kafka-headlessnamespace: kafkalabels:app: kafka spec:type: C…...
 组合)
(C++回溯01) 组合
77、组合 回溯题目三步走 1. 确定参数 2. 确定终止条件 3. for 循环横向遍历,递归纵向遍历 class Solution { public:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex) {if(path.size() k) {…...

k8s学习笔记——安装istio的仪表盘之prometheus安装
接上一篇,继续安装istio的dashboard。 先到istio-1.22.0/samples/addons目录下,把yaml文件中的镜像仓库地址修改了,修改地址参考我之前写的CSDN里的镜像对照表。不然直接执行kubectl apply -f samples/addons这个命令后,依据会出…...

四、GD32 MCU 常见外设介绍 (7) 7.I2C 模块介绍
7.1.I2C 基础知识 I2C(Inter-Integrated Circuit)总线是一种由Philips公司开发的两线式串行总线,用于内部IC控制的具有多端控制能力的双线双向串行数据总线系统,能够用于替代标准的并行总线,连接各种集成 电路和功能模块。I2C器件能够减少电…...
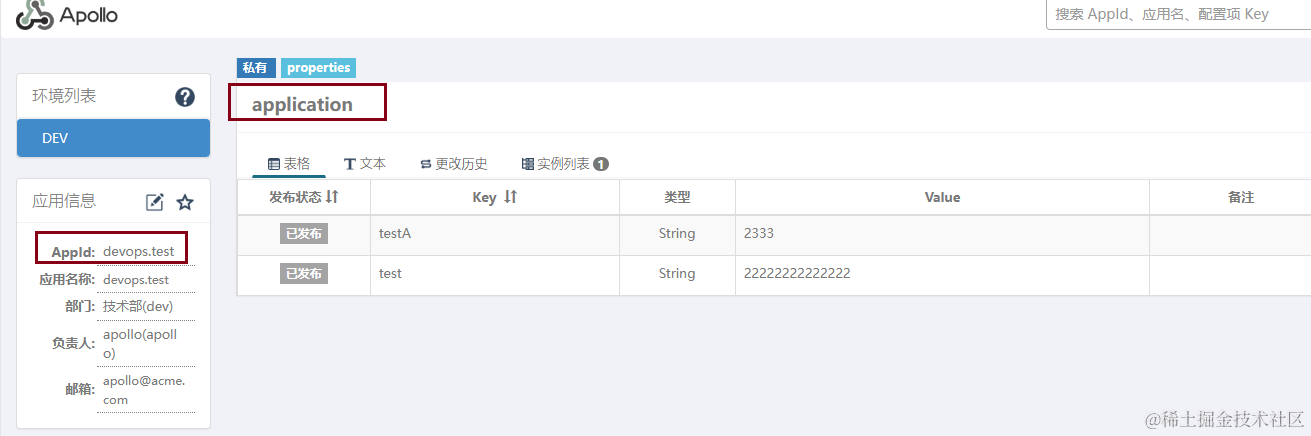
Apollo 配置中心的部署与使用经验
前言 Apollo(阿波罗)是携程开源的分布式配置管理中心。 本文主要介绍其基于 Docker-Compose 的部署安装和一些使用的经验 特点 成熟,稳定支持管理多环境/多集群/多命名空间的配置配置修改发布实时(1s)通知到应用程序支…...

Perl中的设计模式革新:命令模式的实现与应用
Perl中的设计模式革新:命令模式的实现与应用 在面向对象编程中,设计模式是解决特定问题的成熟模板。命令模式作为行为设计模式之一,它将请求封装为对象,从而允许用户根据不同的请求对客户进行参数化。本文将深入探讨如何在Perl中…...

Java8-求两个集合取交集
在Java8中,求两个集合的交集可以使用不同的三种方式:传统的循环遍历、使用Stream API的filter操作和使用Stream API的Collection操作。 方法一:传统的循环遍历 首先,我们创建两个集合list1和list2,并给它们添加一些元…...

爬虫学习4:爬取王者荣耀技能信息
爬虫:爬取王者荣耀技能信息(代码和代码流程) 代码 # 王者荣耀英雄信息获取 import time from selenium import webdriver from selenium.webdriver.common.by import By if __name__ __main__:fp open("./honorKing.txt", "…...

在Ubuntu 14.04上安装和使用Memcache的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 随着您的网站的增长和流量的增加,最快显示压力的组件之一是后端数据库。如果您的数据库没有分布式和配置来处理高负载…...

PCDN技术如何降低运营成本?
PCDN技术通过以下几种方式降低运营商的运营成本: 1.利用用户设备作为缓存节点: PCDN技术将用户设备纳入内容分发网络,利用这些设备的闲置带宽和存储资源来缓存和分发内容。这种方式不需要运营商投入大量的高成本服务器和带宽资源,从而降低了硬件和带宽…...

服务器数据恢复—V7000存储硬盘故障脱机的数据恢复案例
服务器存储数据恢复环境: 某品牌P740小型机AIXSybaseV7000磁盘阵列柜,磁盘阵列柜中有12块SAS机械硬盘(其中包括一块热备盘)。 服务器存储故障: 磁盘阵列柜中有一块磁盘出现故障,运维人员用新硬盘替换掉故障…...

BSV区块链在人工智能时代的数字化转型中的角色
发表时间:2024年6月13日 企业数字化转型已有约30年的历史,而人工智能(以下简称AI)将这种转型提升到了一个全新的高度。这并不难理解,因为AI终于使企业能够发挥其潜力,实现更宏大的目标。然而࿰…...
加载与修改)
android audio 相机按键音:(二)加载与修改
相机按键音资源,加载文件路径: frameworks/av/services/camera/libcameraservice/CameraService.cpp 按键音,加载函数: void CameraService::loadSoundLocked(sound_kind kind) { ATRACE_CALL(); LOG1("Cam…...

Linux grep技巧 提取log中的json数据
目录 一. 前提1.1 数据准备1.2 需求1.3 分析 二. 数据提取2.1 提取所有的json数据2.2 提取子项目的全部json数据2.3 提取指定项目的json数据 一. 前提 1.1 数据准备 545-1 2024/07/20 18:20:21 [ERROR] MPX001 eventControlleraupay transactionIdA545 {"event":&q…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...
