数据结构之深入理解简单选择排序:原理、实现与示例(C,C++)
文章目录
- 一、简单选择排序原理
- 二、C/C++代码实现
- 总结:

在计算机科学中,排序算法是一种非常基础且重要的算法。简单选择排序(Selection Sort)作为其中的一种,因其实现简单、易于理解而受到许多初学者的喜爱。本文将详细介绍简单选择排序的原理、实现过程,并通过C/C++代码示例来加深理解。
一、简单选择排序原理
简单选择排序的基本思想是:首先在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法步骤:
- 初始状态:给定待排序的序列 arr,包含 n 个元素。
- 第一次遍历:从第一个元素开始,依次与后面的元素比较,找到最小的元素,将其与第一个元素交换位置。
- 第二次遍历:从第二个元素开始,依次与后面的元素比较,找到最小的元素,将其与第二个元素交换位置。
- 重复步骤2和步骤3,直到倒数第二个元素和最后一个元素比较完毕。
这样经过 n-1 次遍历后,整个序列就排好序了。
算法分析:
- 时间复杂度:选择排序的时间复杂度为 O(n^2),其中 n 是数据元素的个数。虽然时间复杂度比较高,但是它的实现思路简单,适合于数据量较小的情况。
- 空间复杂度:选择排序是一种原地排序,空间复杂度为 O(1)。
- 稳定性:简单选择排序是一种不稳定的排序算法,即可能改变相同元素的相对顺序。
二、C/C++代码实现
以下是简单选择排序的C代码实现:
#include <stdio.h>void selectionSort(int arr[], int n) {int i, j, min_index, temp;for (i = 0; i < n - 1; i++) {// 初始化最小值索引min_index = i;// 遍历未排序序列,找到最小值索引for (j = i + 1; j < n; j++) {if (arr[j] < arr[min_index]) {min_index = j;}}// 交换最小值与未排序序列的第一个元素if (min_index != i) {temp = arr[i];arr[i] = arr[min_index];arr[min_index] = temp;}}
}int main() {int arr[] = {64, 25, 12, 22, 11};int n = sizeof(arr) / sizeof(arr[0]);selectionSort(arr, n);printf("Sorted array: \n");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}
代码解析
- 函数selectionSort接收一个整型数组arr和数组长度n作为参数。
- 外层循环控制排序的趟数,共进行n-1趟排序。
- 内层循环寻找未排序序列中的最小值索引。
- 如果找到的最小值索引不是当前外层循环的起始索引,则交换这两个位置的元素。
- 主函数main中,定义了一个待排序的数组,调用selectionSort函数进行排序,并输出排序后的结果。
下面是用 C++ 编写的简单选择排序的示例代码:
#include <iostream>void selectionSort(int arr[], int n) {int i, j, minIndex;for (i = 0; i < n - 1; i++) {// 找到未排序部分的最小元素minIndex = i;for (j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 将最小元素与当前位置交换if (minIndex != i) {std::swap(arr[i], arr[minIndex]);}}
}int main() {int arr[] = {64, 25, 12, 22, 11};int n = sizeof(arr) / sizeof(arr[0]);std::cout << "Original array:" << std::endl;for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}std::cout << std::endl;selectionSort(arr, n);std::cout << "Sorted array:" << std::endl;for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}std::cout << std::endl;return 0;
}
解析示例代码:
- selectionSort 函数实现了选择排序算法。外层循环控制待排序部分的起始位置,内层循环用来找到最小元素的索引。
- std::swap 函数用于交换数组中的两个元素。
- main 函数演示了如何使用 selectionSort 函数对数组进行排序,并输出结果。
结果:
运行上述代码,输出如下结果:
Original array:
64 25 12 22 11
Sorted array:
11 12 22 25 64
这证明了选择排序成功地将输入的数组从小到大进行了排序。
总结:
简单选择排序虽然在大数据量下效率不高,但它易于理解和实现,是理解排序算法基本思想的良好起点。在实际应用中,如果数据量较小或者对排序稳定性要求不高,选择排序可以作为一种简单有效的选择。
相关文章:

数据结构之深入理解简单选择排序:原理、实现与示例(C,C++)
文章目录 一、简单选择排序原理二、C/C代码实现总结: 在计算机科学中,排序算法是一种非常基础且重要的算法。简单选择排序(Selection Sort)作为其中的一种,因其实现简单、易于理解而受到许多初学者的喜爱。本文将详细介…...
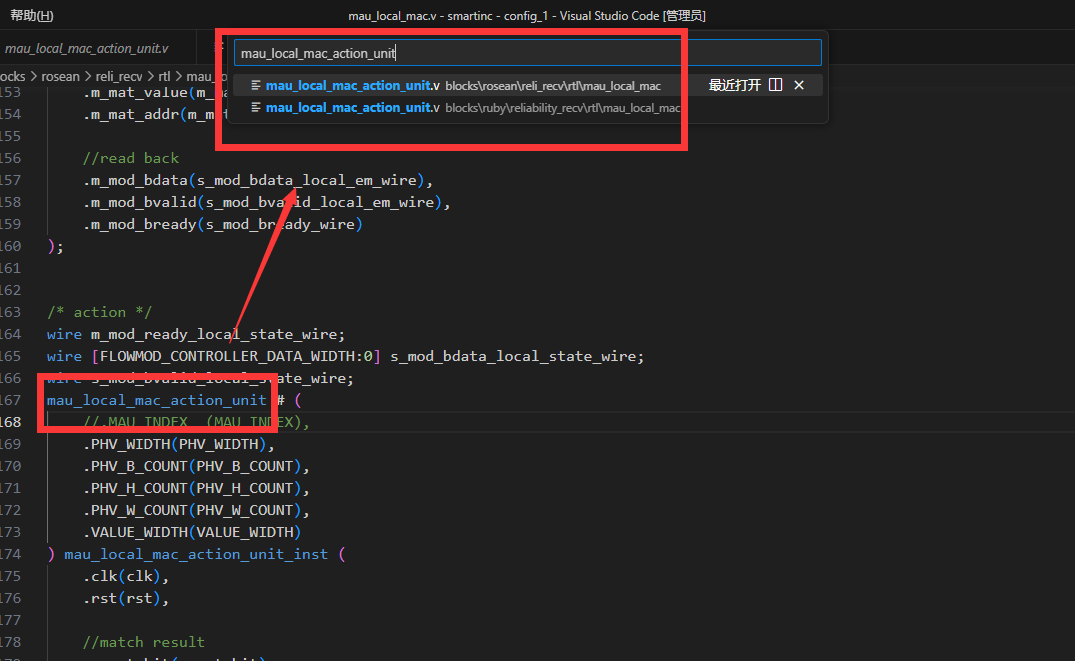
使用vscode搜索打开的文件夹下的文件
右键空白处打开命令面板 摁一次删除键,删除掉图中的大于号 这样就能够找到例化的模块,文件具体在哪个位置,然后打开了...

力扣778.水位上升的泳池中游泳
力扣778.水位上升的泳池中游泳 二分 bfs class Solution {int dx[4] {1,0,-1,0},dy[4] {0,1,0,-1};public:int swimInWater(vector<vector<int>>& grid) {int n grid.size();auto check [&](int mid) -> bool{queue<pair<int,int>>…...
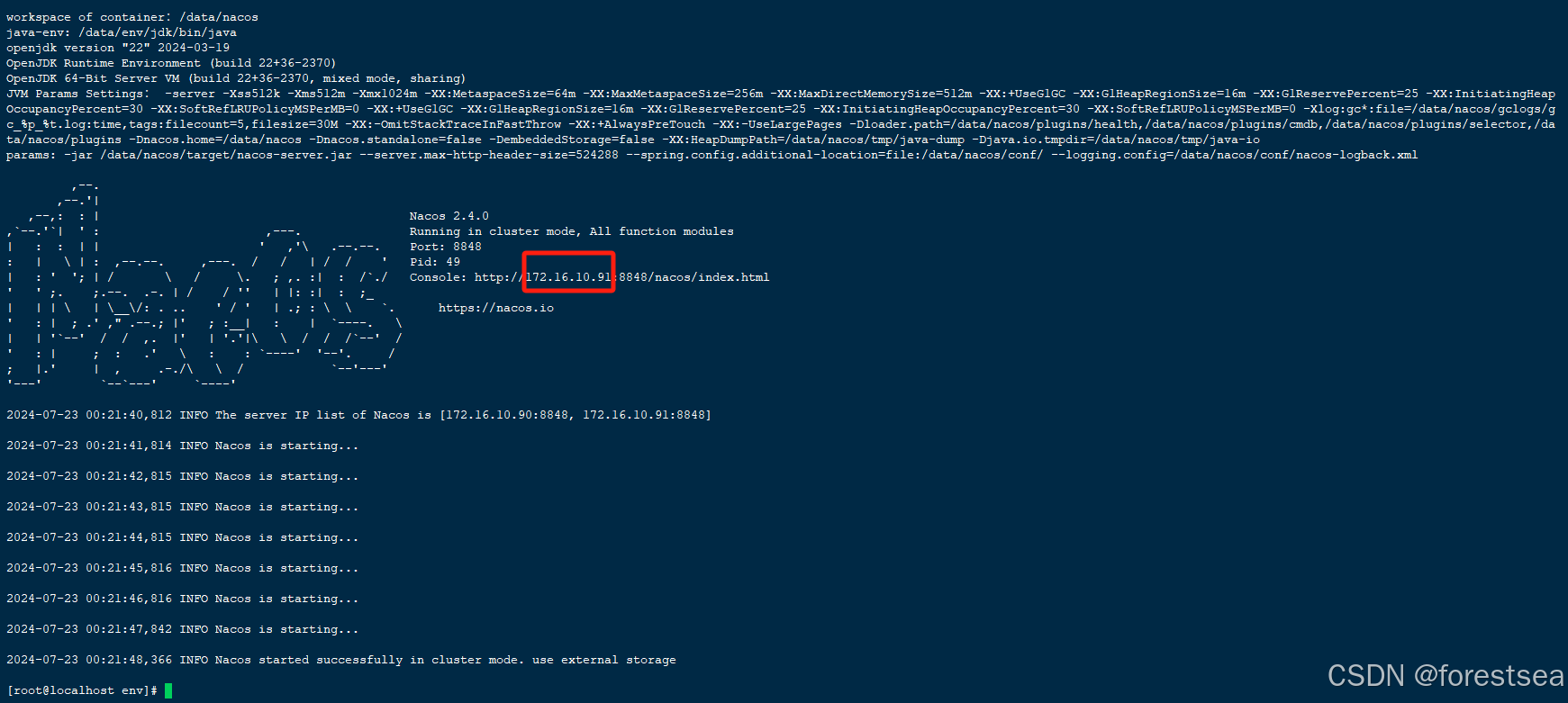
Nacos-2.4.0最新版本docker镜像,本人亲自制作,部署十分方便,兼容postgresql最新版本17和16,奉献给大家了
基于Postgresql数据库存储的nacos最新版本2.4.0,采用docker镜像安装方式 因业务需要,为了让nacos支持postgresql,特意花了两天时间修改了源码,然后制作了docker镜像,如果你也在找支持postgresql的nacos最新版本,恭喜你,你来的正好~ nacos-2.4.0 postgresql的数据库脚本…...

Halcon机器视觉15种缺陷检测案例_9找出所有网格顶点的位置
Halcon机器视觉15种缺陷检测案例_9找出所有网格顶点的位置 效果 原图 代码 *9找出所有网格顶点的位置 dev_update_off ()read_image (Image, 9找出所有风格顶点的位置) get_image_size (Image, Width, Height) *关闭已打开的窗口 dev_close_window ()dev_open_window (0, 0, …...
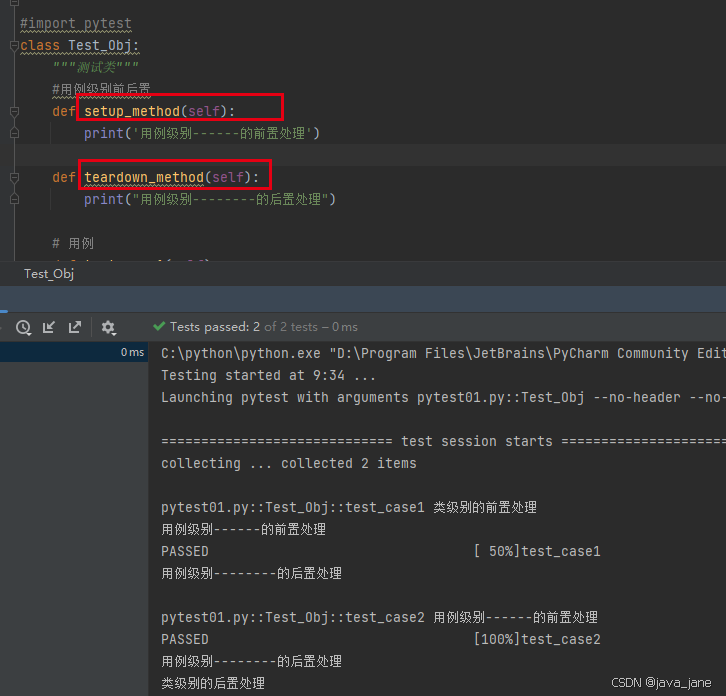
w30-python02-pytest入门
代码如下: import pytest class Test_Obj:"""测试类"""#用例级别前后置def setup(self):print(用例级别------的前置处理)def teardown(self):print("用例级别--------的后置处理")# 用例def test_case1(self):print(&quo…...

WPF+Mvvm项目入门完整教程-仓储管理系统(二)
目录 一、搭建一个主界面框架二、实现步骤1.主界面区域划分2.主界面区域实现 一、搭建一个主界面框架 主要实现主界面的框架样式和基础功能。这里特别说明一下,由于MvvmLight 已经过时不在维护,本项目决定将MvvmLight框架变更为 CommunityToolkit.Mvvm …...

SkyWalking入门搭建【apache-skywalking-apm-10.0.0】
Java学习文档 视频讲解 文章目录 一、准备二、服务启动2-1、Nacos启动2-2、SkyWalking服务端启动2-3、SkyWalking控制台启动2-4、自定义服务接入 SkyWalking 三、常用监控3-1、服务请求通过率3-2、服务请求拓扑图3-3、链路 四、日志配置五、性能剖析六、数据持久化6-1、MySQL持…...

exo项目目录架构
目录 .yml 文件是 YAML(YAML Aint Markup Language) exo项目目录架构 文件作用 topology、viz:项目拓扑结构可视化相关的代码或工具。 项目目录架构 文件作用 .yml 文件是 YAML(YAML Aint Markup Language) 文件的扩展名,YAML 是一种人类可读的数据序列化标准,通…...

mysql中where与on区别
WHERE子句 作用范围:WHERE子句主要用于过滤FROM子句返回的结果集。它可以在SELECT、UPDATE、DELETE语句中使用,以限制哪些行被包含在最终的查询结果中,或者哪些行被更新或删除。应用场景:当需要基于某些条件过滤结果集时…...
)
filebeat把日志文件上传到Es中配置(ES7版本)
默认的filebeat配置会把所有的索引都放到一个文件中,通过摸索发现可以自定义索引的名字、模板、生命周期 (重点注意)该配置文件只适应于ES版本是7,不适应于8的版本,两个版本的配置文件差异很大 /app/logs/info.log日…...

Vue Router基础
Router 的作用是在单页应用(SPA)中将浏览器的URL和用户看到的内容绑定起来。当用户在浏览不同页面时,URL会随之更新,但页面不需要从服务器重新加载。 1 Router 基础 RouterView RouterView 用于渲染当前URL路径对应的路由组件。…...

Apache压测工具ab(Apache Bench)工具的下载安装和使用示例
场景 Jmeter进行http接口压力测试: Jmeter进行http接口压力测试_接口压测两万量-CSDN博客 上面讲压测工具Jmeter的使用,下面介绍另外一个ab(Apache Bench)压测工具的使用。 apache bench apache bench是apache自带的压力测试工具。 ab不仅可以对ap…...

IPIDEA与Python爬虫:联手解锁全球电商数据宝库
IPIDEA与Python爬虫:联手解锁全球电商数据宝库 如何运用代理IP在电商领域进行高效数据采集。特别是在遭遇访问限制的情况下,如何优雅地绕过那些恼人的访问管理机制。当然,在我们的探险之旅中,开源神器PlugLink也将适时出场&#…...

Fine-BI学习笔记
官方学习文档:快速入门指南- FineBI帮助文档 FineBI帮助文档 (fanruan.com) 1.零基础入门 1.1 功能简介 完成四个流程:新建分析主题、添加数据、分析数据、分享协作。 示例数据获取:5分钟上手FineBI - FineBI帮助文档 (fanruan.com) 1.2 …...

AI 辅助编程 Coding AI 辅助研发组织的技术蓝图
简简单单 Online zuozuo:欢迎商业合作 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo :联系我们:VX :tja6288 / EMAIL: 347969164@qq.com 文章目录 AI 辅助编程 Coding A…...

VScode 批量操作
VScode 批量操作 批量修改 按住 alt/option 键, 选择需要批量操作的位置 如果是多行,则按住 altshift 键 可以直接操作 但是有时候比如变量命名,可能需要递增操作的命名 需要下载插件 Increment Selection 按照1的方法多选光标之后&am…...

【Linux】管道通信和 system V 通信
文章目录 一、进程通信原理(让不同进程看到同一份资源)二、管道通信2.1 管道原理及其特点2.1 匿名管道和命名管道 三、共享内存通信3.1 共享内存原理3.2 创建和关联共享内存3.3 去关联、ipc 指令和删除共享内存 四、消息队列和信号量(了解&am…...

Python | Leetcode Python题解之第279题完全平方数
题目: 题解: class Solution { public:// 判断是否为完全平方数bool isPerfectSquare(int x) {int y sqrt(x);return y * y x;}// 判断是否能表示为 4^k*(8m7)bool checkAnswer4(int x) {while (x % 4 0) {x / 4;}return x % 8 7;}int numSquares(i…...

mysql定时备份
为什么写这篇文章 最近项目里面需要定时备份mysql的数据,网上找了下,找到了一些比较好的解决方案。但是发现有几个地方与自己不匹配,我期望有如下 备份过程不能锁表,网上很多都是会锁表备份定时任务无法执行,但是手动…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
