数字图像处理笔记（三) ---- 傅里叶变换的基本原理
系列文章目录
数字图像处理笔记（一）---- 图像数字化与显示
数字图像处理笔记（二）---- 像素加图像统计特征
数字图像处理笔记（三) ---- 傅里叶变换的基本原理
文章目录
- 系列文章目录
- 前言
- 一、傅里叶变换
- 二、离散傅里叶变换的数学公式。
- 三、离散傅里叶变换的应用
- 总结
前言
一、傅里叶变换
问题的引入
信号分解的目的：简化原信号的处理
正选曲线具备良好的保真度。
傅里叶变换就是将现实世界中的时域信号或空域信号，分解成一系列不同频率的正弦波和余弦波之和。
对于一个方波信号，傅里叶变换就是将其分解成几个不同频率的正弦曲线的叠加和，我们将这些正弦曲线展开，将每个正弦曲线的幅度和频率映射到一个平面上就能得到这个方波信号的频谱。
二、离散傅里叶变换的数学公式。
离散傅里叶变换（Discrete Fourier Transform, DFT）是一种数学变换，它将一个信号从时间域转换到频率域，从而分析信号的频谱特性和频率成分。
傅里叶变换：将时域信号 f(n) 转换为频域信号 F(u)。
傅里叶反变换：如何从频域信号 F(u) 还原回时域信号 f(n)
对于二维图像信号 f(m,n)，
傅里叶变换：二维图像信号从空间域转换到频率域
傅里叶反变换：从频率域到空间域的转换
图像经过傅里叶变换后得到的频谱是复数；
图像中低频成分具有较高的能量；
空域与频域的对应关系——一对所有；
频谱
频谱是频率谱密度的简称，是频率的分布曲线。复杂振荡分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱。
三、离散傅里叶变换的应用
总结
• 图像的空域与频域对应是一对所有的关系；
• 相位谱包含了图像的结构信息，频率谱反映了信号能量的分布；
• 频域采样间隔的设置也要遵循Niquest采样定理；
• 低于采样定理的采样频率将导致重建空域图像的折叠伪影
相关文章：
数字图像处理笔记（三) ---- 傅里叶变换的基本原理
系列文章目录 数字图像处理笔记（一）---- 图像数字化与显示 数字图像处理笔记（二）---- 像素加图像统计特征 数字图像处理笔记（三) ---- 傅里叶变换的基本原理 文章目录 系列文章目录前言一、傅里叶变换二、离散傅里叶变…...
Golang | Leetcode Golang题解之第268题丢失的数字
题目： 题解： func missingNumber(nums []int) int {n : len(nums)total : n * (n 1) / 2arrSum : 0for _, num : range nums {arrSum num}return total - arrSum }...
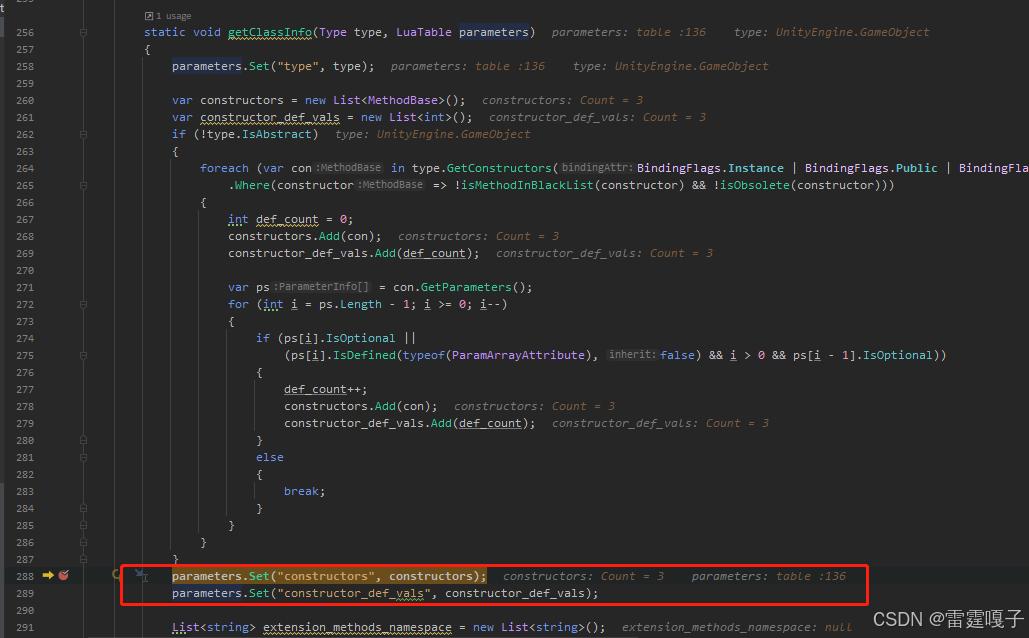
Xlua原理 二
一已经介绍了初步的lua与C#通信的原理，和xlua的LuaEnv的初始化内容。 这边介绍下Wrap文件。 一.Wrap介绍 导入xlua后可以看到会多出上图菜单。 点击后生成一堆wrap文件，这些文件是lua调用C#时进行映射查找用的中间代码。这样就不需要去反射调用节约性…...
《数据结构》--顺序表
C语言语法基础到数据结构与算法，前面已经掌握并具备了扎实的C语言基础，为什么要学习数据结构课程？--我们学完本章就可以实践一个：通讯录项目 简单了解过后，通讯录具备增加、删除、修改、查找联系人等操作。要想实现通…...
Qt：愚蠢的qmake
博主参与了一个使用qmake构建的项目，包含几百个源文件，最近遇到一个恼人的问题：有时仅仅修改了一个.cpp文件，构建项目时就有可能触发全编译。但是编译时又会命中ccache的缓存，这说明源代码实际上内容并没有发生变化。即…...
Apache Dubbo：分布式服务框架的深度解析
文章目录 引言官网链接Dubbo 原理架构概览通信协议负载均衡 基础使用1. 引入依赖2. 配置服务提供者3. 配置服务消费者4. 配置注册中心 高级使用1. 集群容错2. 泛化引用3. 异步调用 优缺点优点缺点 结论 引言 Apache Dubbo 是一个高性能、轻量级的开源 Java RPC 框架。它提供了…...
【前端学习】CSS三大特性
CSS三大特性 CSS的三大特性是为了化简代码、定位问题并且解决问题 继承性 继承性特点： 子级默认继承父级的文字控制属性。注意：如果标签自己有样式则生效自己的样式，不继承。 <!DOCTYPE html> <html lang"en"><…...
了解网络是如何运作
“Web 的工作原理”提供了一个简化的视图，用于了解在计算机或手机上的 Web 浏览器中查看网页时发生的情况。 这个理论对于短期内编写 Web 代码来说并不是必需的，但不久之后，你就会真正开始从理解后台发生的事情中受益。 客户端和服务器 连接到 Internet 的计算机称为客户端和…...
传输层协议——TCP
TCP协议 TCP全称为“传输控制协议”，要对数据的传输进行一个详细的控制。 特点 面向连接的可靠性字节流 TCP的协议段格式 源/目的端口：表示数据从哪个进程来，到哪个进程4位首部长度：表示该TCP头部有多少字节（注意它…...
C++相关概念和易错语法（23）（set、仿函数的应用、pair、multiset）
1.set和map存在的意义 （1）set和map的底层都是二叉搜索树，可以达到快速排序（当我们按照迭代器的顺序来遍历set和map，其实是按照中序来遍历的，是排过序的）、去重、搜索的目的。 （2&a…...
netty入门-3 EventLoop和EventLoopGroup，简单的服务器实现
文章目录 EventLoop和EventLoopGroup服务器与客户端基本使用增加非NIO工人NioEventLoop 处理普通任务与定时任务 结语 EventLoop和EventLoopGroup 二者大概是什么这里不再赘述，前一篇已简述过。 不理解也没关系。 下面会简单使用，看了就能明白是什么 这…...
通信原理-思科实验五：家庭终端以太网接入Internet实验
实验五 家庭终端以太网接入Internet实验 一实验内容 二实验目的 三实验原理 四实验步骤 1.按照上图选择对应的设备，并连接起来 为路由器R0两个端口配置IP 为路由器R1端口配置IP 为路由器设备增加RIP，配置接入互联网的IP的动态路由项 5.为路由器R1配置静…...
【Vue】vue概述
1、简介 Vue.js（简称Vue）是一款用于构建用户界面的渐进式JavaScript框架。由前Google高级软件工程师尤雨溪（Evan You）于2014年创建，是一个独立且社区驱动的开源项目。Vue.js基于标准的HTML、CSS和JavaScriptÿ…...
Docker use experience
#docker command docker load -i <镜像文件.tar> docker run -it -d --name 容器名 -p 宿主机端口:容器端口 -v 宿主机文件存储位置:容器内文位置 镜像名:Tag /bin/bash docker commit -m"提交的描述信息" -a"作者" 容器ID 要…...
Android平台RTSP|RTMP直播播放器技术接入说明
技术背景 大牛直播SDK自2015年发布RTSP、RTMP直播播放模块，迭代从未停止，SmartPlayer功能强大、性能强劲、高稳定、超低延迟、超低资源占用。无需赘述，全自研内核，行业内一致认可的跨平台RTSP、RTMP直播播放器。本文以Android平台…...
数据结构——栈（顺序结构）
一、栈的定义 栈是一种数据结构，它是一种只能在一端进行插入和删除操作的特殊线性表。这一端被称为栈顶，另一端被称为栈底。栈按照后进先出（LIFO）的原则进行操作（类似与手枪装弹后射出子弹的顺序）。在计算…...
速盾：cdn能防御ddos吗？
CDN（内容分发网络）是一种广泛应用于互联网中的技术，它通过将内容分发到全球各地的服务器上，以提高用户在访问网站时的加载速度和稳定性。然而，CDN是否能够有效防御DDoS（分布式拒绝服务）攻击是一…...
分享 2 个 .NET EF 6 只更新某些字段的方法
前言 EF 更新数据时，通常情况下，是更新全部字段的，但实际业务中，更新全部字段的情况其实很少，一般都是修改其中某些字段，所以为了实现这个目标，很多程序员通常会这样作： 先从数据库…...
vs code解决报错 （c/c++的配置环境 远端机器为Linux ubuntu）
参考链接：https://blog.csdn.net/fightfightfight/article/details/82857397 https://blog.csdn.net/m0_38055352/article/details/105375367 可以按照步骤确定那一步不对，如果一个可以就不用往下看了 目录 一、检查一下文件扩展名 二、安装扩展包并…...
08 字符串和字节串
使用单引号、双引号、三单引号、三双引号作为定界符（delimiter）来表示字符串，并且不同的定界符之间可以相互嵌套。 很多内置函数和标准库对象也都支持对字符串的操作。 x hello world y Python is a great language z Tom said, "Le…...
生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式，可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1） にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために ＆ ように（３）そう（４）にする3、…...
day52 ResNet18 CBAM
在深度学习的旅程中，我们不断探索如何提升模型的性能。今天，我将分享我在 ResNet18 模型中插入 CBAM（Convolutional Block Attention Module）模块，并采用分阶段微调策略的实践过程。通过这个过程，我不仅提升…...
通过Wrangler CLI在worker中创建数据库和表
官方使用文档：Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后，会在本地和远程创建数据库： npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库： 现在，您的Cloudfla…...
【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06（十亿美元）。漏洞扫描服务市场行业预计将从 2024 年的 3.48（十亿美元）增长到 2032 年的 9.54（十亿美元）。预测期内漏洞扫描服务市场 CAGR（增长率&…...
视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞！！！ 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用，因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型（VLMs）在字幕生成方面…...
鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发，使用DevEco Studio作为开发工具，采用Java语言实现，包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT，橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版：职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
面向无人机海岸带生态系统监测的语义分割基准数据集
描述：海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而，目前该领域仍面临一个挑战，即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...