【基础算法总结】优先级队列
优先级队列
- 1.最后一块石头的重量
- 2.数据流中的第 K 大元素
- 4.前K个高频单词
- 4.数据流的中位数

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.最后一块石头的重量
题目链接:1046. 最后一块石头的重量
题目分析:

每一回合,从中选出两块 最重的 石头,x == y,那么两块石头都会被完全粉碎;如果 x != y,那么重量较小的 x 石头将会完全粉碎,而重量较大的 y 的石头新重量为 y-x。最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。

算法原理:
每次挑选的是先挑一堆数中最大的那个数,然后再挑一个剩下数中最大的数。这不正好符合大根堆的数据结构吗。
解法:用堆来模拟这个过程
先拿数组的数创建一个大根堆,每次从堆里面选择最大和次大两个数,如果相等就是0不用加入到大根堆里,如果不相等用最大的数减去次大的数,把结果加入到堆里面。如果最后堆里还剩下一个数,返回这个数。如果堆为空说明石头全都粉碎了返回0即可。
class Solution {
public:int lastStoneWeight(vector<int>& stones) {//1.拿元素创建一个大根堆priority_queue<int> heap(stones.begin(),stones.end());//2.模拟这个过程while(heap.size() >= 2){int s1 = heap.top();heap.pop();int s2 = heap.top();heap.pop();if(s1 != s2) heap.push(s1 - s2);}return heap.size() ? heap.top() : 0;}
};
2.数据流中的第 K 大元素
题目链接:703. 数据流中的第 K 大元素
题目分析:

设计一个找到数据流中第 k 大元素的类(class)。注意是排序后的第 k 大元素,不是第 k 个不同的元素。

int add(int val) 将 val 插入数据流 nums 后,返回当前数据流中第 k 大的元素。

算法原理:
这道题其实考察的是一个非常经典的问题, TopK问题。
关于TopK问题有两种解题思路,一种是堆,一种是前面刚学的快速选择算法。快速选择排序虽然快,但是对于海量的数据内存根本放不下。所以在海量数据情况最优的还是堆。

解法:用 堆 来解决
- 创建一个大小为 k 的堆(大根堆 or 小根堆)
- 循环
1.依次进堆
2.判断堆的大小是否超过 K
在堆的实现,画图和代码分析建堆,堆排序,时间复杂度以及TOP-K问题,对于求第K个最大元素,我们也是将前K个数建个小堆,然后将剩下的N-K个元素和堆顶元素做比较,如果大于堆顶元素,就先把栈顶元素pop掉,也就是把堆中最小元素删除,然后将它放进去。这样一直循环,直到所有元素都比较完成。因为是一直把堆中最小的pop掉,那堆的元素就是N个元素中最大的,而堆顶就是第K个最大的元素,别忘记我们这是一个小堆!
这里我们也是建小堆,依次进堆,当堆大小超过K个,pop堆顶元素,把堆中最小元素pop掉,并且使堆保持K个大小。每次都是堆中最小元素去掉。那最后堆中剩下的就是前K个最大元素,而堆顶就是第K个最大元素。
考虑一下下面两个问题
- 用大根堆还是小根堆
- 为什么要用大根堆(小根堆)
class KthLargest {
public:priority_queue<int,vector<int>,greater<int>> heap;int _k;KthLargest(int k, vector<int>& nums) {_k = k;for(auto& x : nums){heap.push(x);if(heap.size() > k) heap.pop();}}int add(int val) {heap.push(val);if(heap.size() > _k) heap.pop();return heap.top();}
};
4.前K个高频单词
题目链接:692. 前K个高频单词
题目分析:

这是一个TopK的问题,注意,返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序(由低向高) 排序。
算法原理:
解法:利用 “堆” 来解决 TopK 问题
-
预处理一下原始的字符串数组: 用一个哈希表,统计一下每一个单词出现的频次。
-
创建一个大小为 k 的堆,类提供的比较函数满足不了要求,我们要自己定义一个!(返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序(由低向高) 排序。)如果比较频次创建一个小根堆,如果比较字典序(频次相同的时候)创建一个大根堆。所以说创建堆写比较函数的时候必须要考虑这两点,当频次相同的时候字典序按照大根堆方式比较,当频次不同的时候按照小根堆方式比较。
-
循环
1.依次进堆
2.判断堆的大小是否超过 K -
提取结果
因为求前K大,所以建的是一个小根堆,然后提取堆顶元素在pop是一个升序的。有两种方式拿最终答案,要么逆序一下取前K个,要么从后往前取K个。
class Solution {
public:struct Compare{bool operator()(const pair<string,int>& l,const pair<string,int>& r){//频次不同按照小根堆比较, 频次相同字典序按照大根堆方式比较return l.second > r.second || (l.second == r.second && l.first < r.first);}};vector<string> topKFrequent(vector<string>& words, int k) {vector<string> ret;// 1.统计一下每一个单词的频次map<string,int> count;for(auto& str : words){count[str]++;}// 2.创建一个大小为 k 的小堆priority_queue<pair<string,int>,vector<pair<string,int>>,Compare> heap;// 3.TopK 的主逻辑for(auto& m : count){heap.push(m);if(heap.size() > k) heap.pop();}// 4.提取结果vector<string> tmp;while(!heap.empty()){tmp.push_back(heap.top().first);heap.pop();}reverse(tmp.begin(),tmp.end());for(int i = 0; i < k; ++i)ret.push_back(tmp[i]);return ret;}
};
4.数据流的中位数
题目链接:295. 数据流的中位数
题目分析:

给一个数据流,让返回每次当前已经加入到数组的数据流的中位数。中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。表的大小是奇数,直接返回中间的数。

算法原理:
解法一:直接sort
每次从数据流中来一个数插入数组中之后,都对当前数组进行sort,然后通过下标的方式找到中间数。

每次add加入一个数都要sort,时间复杂度是O(nlogn)。总体时间复杂度是非常恐怖的。因为是下标访问,find 时间复杂度是 O(1)
解法二:插入排序的思想
[0,end] 有序,插入 end + 1,使 [0, end + 1]有序。这道题正好就是这样的思想。

add函数,每次插入一个数的时候都需要从后往前扫描找一个插入的位置,因此时间复杂度是O(n),find 也是通过下标去找 时间复杂度是O(1)
解法三:大小堆来维护数据流的中位数
此时有一个数轴已经按照从小到大的排好序了,这个时候想找中间数的时候。把这些数的前半部分放到一个大根堆里面,后半部分放到小根堆里面。此时找中间值也很快,前面较小的数放到大根堆里面,堆顶元素是数轴中这些较小元素种最右边的值。后面较大的数放到小根堆里面,堆顶元素是数轴中这些较大元素最左边。此时我们仅需根据数组中的元素的个数就可以求出中位数是多少了。如果数组是偶数个大根堆和小根堆正好把数轴平分,然后大堆堆顶元素和小堆堆顶元素相加/2就是这个数组的中位数。如果数组是奇数个。我们就先人为规定一下,数轴左边元素是m个,右边是n个,要么 m == n,要么 m > n (n = n + 1)。如果 m == n 正好平均分。如果数轴个数是奇数个,人为规定左边大根堆多方一个元素,m > n(n = n + 1),此时中位数就是左边大根堆的堆顶元素。

向这样用大根堆存左边较小部分,小根堆存右边较大部分。find 时间复杂度也是O(1),而add快了很多,因为我们是从堆存这些元素的,插入和删除每次调整堆仅需O(logn)
细节问题:
add如何实现:
假设现在有两个堆了。一个大根堆left,一个小根堆right。left元素个数m个,right元素个数n个,left堆顶元素x,right堆定元素y。如果此时来了一个数num,num要么放在left里,要么放在right里。但是放好之后可能会破坏之前的规则:
- m == n
- m > n —> m == n + 1
我们必须维护上面的规则,才能正确找到数组中位数。
接下来分情况讨论:
- m == n
num要么插入left,要么插入right。
如果num要进入left,那么num <= x,但是别忘记 m == n 有可能两个堆全为空,num也是直接进入left。此时 m 比 n 多了一个。没关系直接进就行。
如果num进入right,那条件是 num > x。此时就有问题了。n > m了,而 n > m是不被允许的,所以我们要把右边堆调整一下,就是拿right堆顶元素放到left里。因为right是一个小根堆,堆顶就是最小值。拿到left,还是能保证left堆里元素是较小的,right堆里元素是较大的。拿right堆顶元素放到left里正好满足 m == n + 1。这里有一个细节问题,必须num先进right堆,然后再拿right堆定元素放到left,因为 x < num < y,如果直接把y拿过去了,就破坏了left都是较小元素。right都是较大元素。

- m > n —> m == n + 1
如果num进入left,那么num <= x , 但是此时不满足 m == n + 1,因此 进栈后将栈顶元素给right。
如果num进入right,那么num > x , m == n了,直接进就行了

class MedianFinder {
public:MedianFinder() {}void addNum(int num) {// 分类讨论即可int m = left.size(), n = right.size();if(m == n) // 左右两个堆的元素个数相同{if(m == 0 || num <= left.top())left.push(num);else{right.push(num);left.push(right.top());right.pop();}}else //左边堆的元素个数比右边堆元素个数多 1{if(num <= left.top()){left.push(num);right.push(left.top());left.pop();}elseright.push(num);}}double findMedian() {int m = left.size(), n = right.size();if(m == n) return (left.top() + right.top()) / 2.0;else return left.top();}private: priority_queue<int> left;priority_queue<int,vector<int>,greater<int>> right;
};
相关文章:

【基础算法总结】优先级队列
优先级队列 1.最后一块石头的重量2.数据流中的第 K 大元素4.前K个高频单词4.数据流的中位数 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励,我们一起努力吧!😃😃 1…...

python-绝对值排序(赛氪OJ)
[题目描述] 输入 n 个整数,按照绝对值从大到小排序后输出。保证所有整数的绝对值不同。输入格式: 输入数据有多组,每组占一行,每行的第一个数字为 n ,接着是 n 个整数, n0 表示输入数据的结束,不做处理。输…...

成功者的几个好习惯,你具备了几个
每个人都想成为自己领域的佼佼者,然而,成功并非偶然,它往往与一系列良好的习惯紧密相连。这些习惯如同灯塔,指引着成功者在波涛汹涌的大海中稳健前行。 一、设定明确目标 没有明确的目标,就如同航海没有指南针&#…...

centos中zabbix安装、卸载及遇到的问题
目录 Zabbix简介Zabbix5.0和Zabbix7.0的区别监控能力方面模板和 API 方面性能、速度方面 centos7安装Zabbix(5.0)安装zabbix遇到的问题卸载Zabbix Zabbix简介 Zabbix 是一个基于 WEB 界面的提供分布式系统监视以及网络监视功能的企业级的开源解决方案。zabbix 能监视各种网络参…...

php编译安装
一、基础环境准备 # php使用www用户 useradd -s /sbin/nologin -M www二、下载php包 # 下载地址 https://www.php.net/downloads wget https://www.php.net/distributions/php-8.3.9.tar.gz三、配置编译安装 编译安装之前需要处理必要的依赖,在编译配置安装&…...
)
[K8S] K8S资源控制器Controller Manager(4)
文章目录 1. 常见的Pod控制器及含义2. Replication Controller控制器2.1 部署ReplicaSet 3. Deployment3.1部署Deployment3.2 运行Deployment3.3 镜像更新方式3.4 Deployment扩容3.5 滚动更新3.6 金丝雀发布(灰度发布)3.7 Deployment版本回退3.8 Deployment 更新策略 4. Daemon…...

C#,.NET常见算法
1.递归算法 1.1.C#递归算法计算阶乘的方法 using System;namespace C_Sharp_Example {public class Program{/// <summary>/// 阶乘:一个正整数的阶乘Factorial是所有小于以及等于该数的正整数的积,0的阶乘是1,n的阶乘是n࿰…...

KubeSphere介绍及一键安装k8s
KubeSphere介绍 官网地址:https://kubesphere.io/zh/ KubeSphere愿景是打造一个以 Kubernetes 为内核的云原生分布式操作系统,它的架构可以非常方便地使第三方应用与云原生生态组件进行即插即用(plug-and-play)的集成࿰…...

Spring 系列
SpringBoot 实体类(Entity)层 实体类(Entity)通常属于模型层(Model Layer)或领域层(Domain Layer)。它们代表应用程序中的核心业务数据结构,与数据库表结构紧密对应。在…...

基于opencv[python]的人脸检测
1 图片爬虫 这里的代码转载自:http://t.csdnimg.cn/T4R4F # 获取图片数据 import os.path import fake_useragent import requests from lxml import etree# UA伪装 head {"User-Agent": fake_useragent.UserAgent().random}pic_name 0 def request_pic…...

配置SSH公钥互信
目录 第一台主机:servera(172.25.250.101) 第一步:查看 . ssh目录下面是否为空 第二步:输入命令ssh-keygen 第三步: 再看查看一下. ssh目录 第四步: 输入命令 ssh-copy-id root172.25.250…...
)
WEB渗透Web突破篇-SQL注入(MSSQL)
注释符 -- 注释 /* 注释 */用户 SELECT CURRENT_USER SELECT user_name(); SELECT system_user; SELECT user;版本 SELECT version主机名 SELECT HOST_NAME() SELECT hostname;列数据库 SELECT name FROM master..sysdatabases; SELECT DB_NAME(N); — for N 0, 1, 2, ……...

DAY15
数组 冒泡排序 冒泡排序无疑是最为出名的排序算法之一,总共有八大排序 冒泡的代码还是相当简单的,两层循环,外层冒泡轮数,里层依次比较,江湖中人人尽皆知 我们看到嵌套循环,应该马上就可以得到这个算法的…...

pytest结合allure-pytest插件生成测试报告
目录 一、安装allure-pytest插件 二、下载allure 三、生成allure报告 四、效果展示 一、安装allure-pytest插件 二、下载allure 下载之后解压,解压之后还要配置环境变量(把allure目录下bin目录配置到系统变量的path路径),下…...

详细解析用户提交咨询
上一篇文章中写到了使用Server-Sent Events (SSE),并获取message里面的内容。 本篇文章主要是写,具体该如何实现的具体代码,代码见下方,可直接拿 async submitConsult() {this.scrollToBottom();if (!this.$checkLogin()) return;…...

UDP/TCP协议解析
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...
力扣94题(java语言)
题目 思路 使用一个栈来模拟递归的过程,以非递归的方式完成中序遍历(使用栈可以避免递归调用的空间消耗)。 遍历顺序步骤: 遍历左子树访问根节点遍历右子树 package algorithm_leetcode;import java.util.ArrayList; import java.util.List; import…...

JavaScript基础入门:构建动态Web世界的基石
简要介绍JavaScript作为互联网上最流行的编程语言之一,它在构建交互式网页、动态Web应用及服务器后端(通过Node.js)中的重要性。强调学习JS对于任何想要进入Web开发领域的人来说是不可或缺的。 1. JavaScript是什么? 定义JavaSc…...

01-client-go
想学习K8S源码,可以加 :mkjnnm 1、介绍 client-go 是用来和 k8s 集群交互的go语言客户端库,地址为:https://github.com/kubernetes/client-go client-go 的版本有两种标识方式: v0.x.y (For each v1.x.y Kubernetes…...
WebRTC QoS方法十三.2(Jitter延时的计算)
一、背景介绍 一些报文在网络传输中,会存在丢包重传和延时的情况。渲染时需要进行适当缓存,等待丢失被重传的报文或者正在路上传输的报文。 jitter延时计算是确认需要缓存的时间 另外,在检测到帧有重传情况时,也可适当在渲染时…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...

【靶场】XXE-Lab xxe漏洞
前言 学习xxe漏洞,搭了个XXE-Lab的靶场 一、搭建靶场 现在需要登录,不知道用户名密码,先随便试试抓包 二、判断是否存在xxe漏洞 1.首先登录抓包 看到xml数据解析,由此判断和xxe漏洞有关,但还不确定xxe漏洞是否存在。 2.尝试xxe 漏洞 判断是否存在xxe漏洞 A.send to …...

android关于pthread的使用过程
文章目录 简介代码流程pthread使用hello_test.cppAndroid.bp 编译过程报错处理验证过程 简介 android开发经常需要使用pthread来编写代码实现相关的业务需求 代码流程 pthread使用 需要查询某个linux函数的方法使用,可以使用man 函数名 // $ man pthread_crea…...

gorm 配置数据库
介绍 GORM 是 Go 语言中最流行的 ORM(对象关系映射)库之一,基于数据库操作的封装,提供类似 Django ORM / SQLAlchemy 的开发体验。 特性描述支持多种数据库MySQL、PostgreSQL、SQLite、SQL Server、ClickHouse 等自动迁移自动根…...
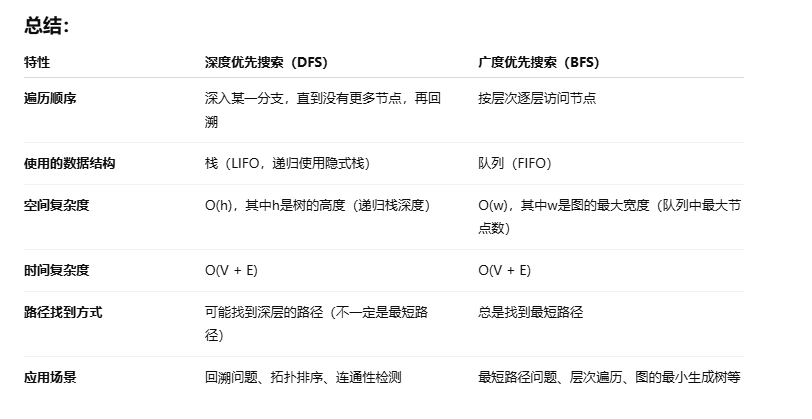
深度优先算法学习
1: 从 1点出发到 15点 #include <stdio.h>#define MAX_NODES 100typedef struct {int node_id;int *nextNodes;int nextNodesSize; } Node;// 假设我们有一个节点数组,全局保存了所有节点 Node nodes[MAX_NODES];void dfs(int node_id) {Node *node &n…...

网页抓取混淆与嵌套数据处理流程
当我们在网页抓取中,遇到混淆和多层嵌套的情况是比较常见的挑战。混淆大部分都是为了防止爬虫而设计的,例如使用JavaScript动态加载、数据加密、字符替换、CSS偏移等。多层嵌套则可能是指HTML结构复杂,数据隐藏在多层标签或者多个iframe中。 …...

STM32+MPU6050传感器
#创作灵感## 在嵌入式系统开发中,STM32F103C8T6单片机与MPU6050传感器的组合因其高性能、低功耗以及丰富的功能而备受青睐。本文将简单介绍如何在Keil 5开发环境中实现STM32F103C8T6与MPU6050的连接和基本数据采集,带你快速入门智能硬件开发。 一、硬件…...
