C#,.NET常见算法
1.递归算法
1.1.C#递归算法计算阶乘的方法
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 阶乘:一个正整数的阶乘Factorial是所有小于以及等于该数的正整数的积,0的阶乘是1,n的阶乘是n!/// </summary>public static void Main(){int result = Factorial(5);Console.WriteLine("5的阶乘是:"+result);Console.ReadLine();}private static int Factorial(int v){if(v == 0 || v == 1){return 1;}else{return v * Factorial(v-1);}}}
}1.2.C#递归算法计算数组的和
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 数组求和/// </summary>public static void Main(){int[] numbers = { 1,2,3,4,5};int sum = ArraySum(numbers,0);Console.WriteLine("数组的和是:"+sum);Console.ReadLine();}private static int ArraySum(int[] arr, int v){if(v>=arr.Length){return 0;}else{return arr[v] + ArraySum(arr, v + 1);}}}
}1.3.C#递归算法实现斐波那契数列第三十位数字
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 实现斐波那契数列的第三十位,已知斐波那契数列1,1,2,3,5,8,自身计算前二个之和/// </summary>public static void Main(){int n = 30;int result = feibonaqi(30);Console.WriteLine("斐波那契数列第三十位是:"+result);Console.ReadLine(); }private static int feibonaqi(int v){if(v <= 0){return 0;}else if(v > 0 && v <=2){return 1;}else{return feibonaqi(v - 1) + feibonaqi(v - 2);}}}
}
1.4.C#递归算法计算1-100的和
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 计算1-100-sum/// </summary>public static void Main(){int result = SumNumber(100);Console.WriteLine("1+2+3+4+...+100="+result);Console.ReadLine(); }private static int SumNumber(int v){if(v ==1){return 1;}else{return v + SumNumber(v-1);}}}
}2.排序算法
2.1.冒泡排序算法
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 双重循环方式实现冒泡排序/// </summary>public static void Main(){int[] arr = { 1,6,4,2,3,9,8,0,7};int arrLength = arr.Length;for(int i =0; i< arr.Length -1; i++){for(int j=0;j<arr.Length-i-1;j++){if(arr[j]>arr[j+1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}}Console.WriteLine("排序后的顺序"+string.Join(",",arr));Console.ReadLine();}}
}2.2. 使用递归算法实现冒牌排序
using System;namespace C_Sharp_Example
{public class Program{/// <summary>/// 递归方式实现冒泡排序/// </summary>public static void RecursiveBubbleSort(int[] arr, int arrLength){if (arrLength == 1)return;for(int i=0; i<arrLength-1;i++){if(arr[i] > arr[i+1]){int tmp = arr[i];arr[i] = arr[i + 1];arr[i + 1] = tmp;}}RecursiveBubbleSort(arr,arrLength-1);}private static void RecursiveBubbleSortRun(){int[] arr = { 1,6,4,2,3,9,8,0,7};int arrLength = arr.Length;RecursiveBubbleSort(arr,arrLength);Console.WriteLine("排序后的结果"+string.Join(",",arr));Console.ReadLine();}}
}
更新中 ~~~ 创作不易,喜欢点赞收藏加关注 ❤
相关文章:

C#,.NET常见算法
1.递归算法 1.1.C#递归算法计算阶乘的方法 using System;namespace C_Sharp_Example {public class Program{/// <summary>/// 阶乘:一个正整数的阶乘Factorial是所有小于以及等于该数的正整数的积,0的阶乘是1,n的阶乘是n࿰…...

KubeSphere介绍及一键安装k8s
KubeSphere介绍 官网地址:https://kubesphere.io/zh/ KubeSphere愿景是打造一个以 Kubernetes 为内核的云原生分布式操作系统,它的架构可以非常方便地使第三方应用与云原生生态组件进行即插即用(plug-and-play)的集成࿰…...

Spring 系列
SpringBoot 实体类(Entity)层 实体类(Entity)通常属于模型层(Model Layer)或领域层(Domain Layer)。它们代表应用程序中的核心业务数据结构,与数据库表结构紧密对应。在…...

基于opencv[python]的人脸检测
1 图片爬虫 这里的代码转载自:http://t.csdnimg.cn/T4R4F # 获取图片数据 import os.path import fake_useragent import requests from lxml import etree# UA伪装 head {"User-Agent": fake_useragent.UserAgent().random}pic_name 0 def request_pic…...

配置SSH公钥互信
目录 第一台主机:servera(172.25.250.101) 第一步:查看 . ssh目录下面是否为空 第二步:输入命令ssh-keygen 第三步: 再看查看一下. ssh目录 第四步: 输入命令 ssh-copy-id root172.25.250…...
)
WEB渗透Web突破篇-SQL注入(MSSQL)
注释符 -- 注释 /* 注释 */用户 SELECT CURRENT_USER SELECT user_name(); SELECT system_user; SELECT user;版本 SELECT version主机名 SELECT HOST_NAME() SELECT hostname;列数据库 SELECT name FROM master..sysdatabases; SELECT DB_NAME(N); — for N 0, 1, 2, ……...

DAY15
数组 冒泡排序 冒泡排序无疑是最为出名的排序算法之一,总共有八大排序 冒泡的代码还是相当简单的,两层循环,外层冒泡轮数,里层依次比较,江湖中人人尽皆知 我们看到嵌套循环,应该马上就可以得到这个算法的…...

pytest结合allure-pytest插件生成测试报告
目录 一、安装allure-pytest插件 二、下载allure 三、生成allure报告 四、效果展示 一、安装allure-pytest插件 二、下载allure 下载之后解压,解压之后还要配置环境变量(把allure目录下bin目录配置到系统变量的path路径),下…...

详细解析用户提交咨询
上一篇文章中写到了使用Server-Sent Events (SSE),并获取message里面的内容。 本篇文章主要是写,具体该如何实现的具体代码,代码见下方,可直接拿 async submitConsult() {this.scrollToBottom();if (!this.$checkLogin()) return;…...

UDP/TCP协议解析
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...
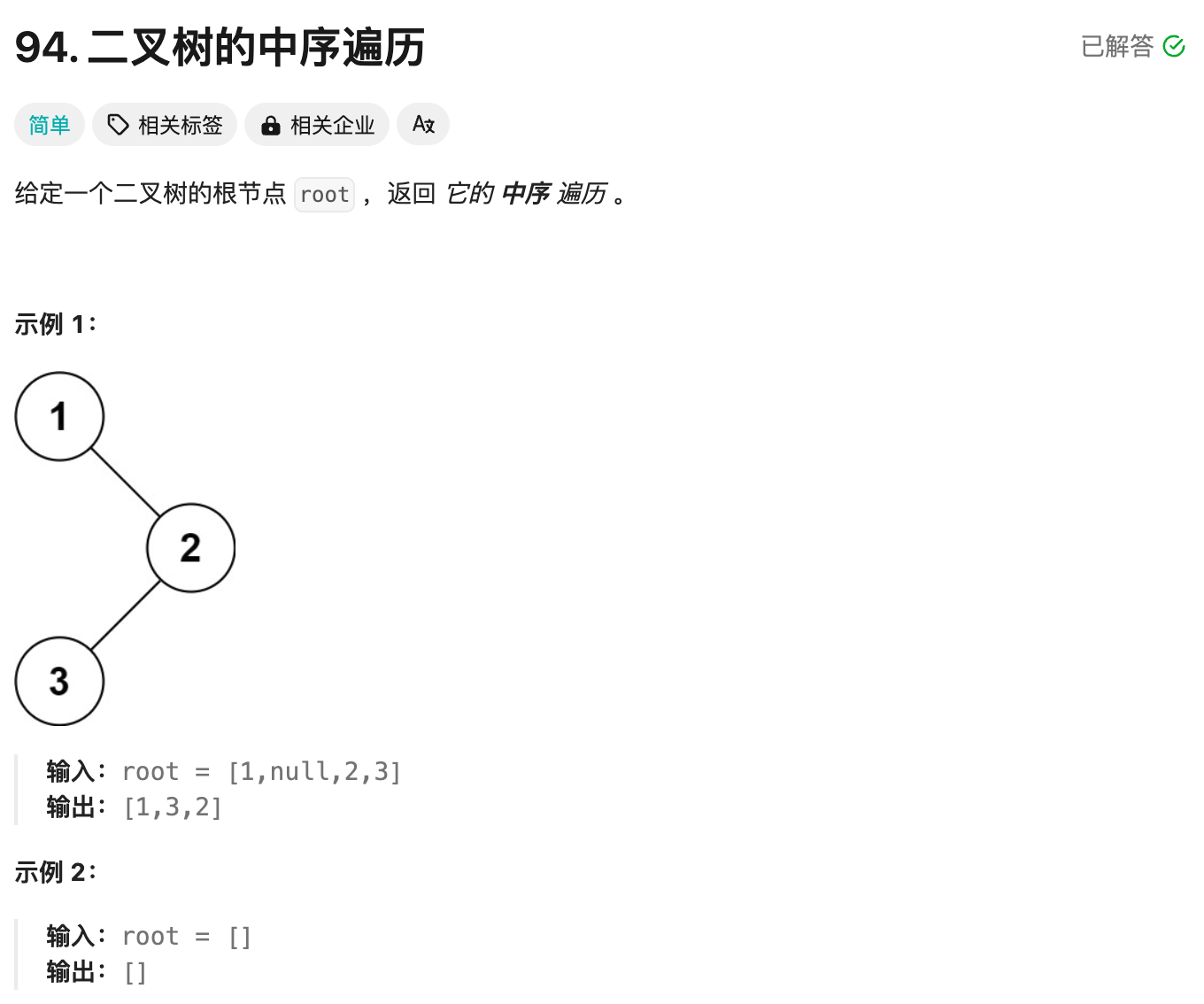
力扣94题(java语言)
题目 思路 使用一个栈来模拟递归的过程,以非递归的方式完成中序遍历(使用栈可以避免递归调用的空间消耗)。 遍历顺序步骤: 遍历左子树访问根节点遍历右子树 package algorithm_leetcode;import java.util.ArrayList; import java.util.List; import…...

JavaScript基础入门:构建动态Web世界的基石
简要介绍JavaScript作为互联网上最流行的编程语言之一,它在构建交互式网页、动态Web应用及服务器后端(通过Node.js)中的重要性。强调学习JS对于任何想要进入Web开发领域的人来说是不可或缺的。 1. JavaScript是什么? 定义JavaSc…...

01-client-go
想学习K8S源码,可以加 :mkjnnm 1、介绍 client-go 是用来和 k8s 集群交互的go语言客户端库,地址为:https://github.com/kubernetes/client-go client-go 的版本有两种标识方式: v0.x.y (For each v1.x.y Kubernetes…...
WebRTC QoS方法十三.2(Jitter延时的计算)
一、背景介绍 一些报文在网络传输中,会存在丢包重传和延时的情况。渲染时需要进行适当缓存,等待丢失被重传的报文或者正在路上传输的报文。 jitter延时计算是确认需要缓存的时间 另外,在检测到帧有重传情况时,也可适当在渲染时…...

PHP进阶:前后端交互、cookie验证、sql与php
单词:construct 构造 destruct 摧毁 empty 空的 trim 修剪 strip 清除 slash 斜线 special 特殊 char 字符 query 询问 构造方法(魔术方法) 构造方法是一种特殊的函数࿰…...

优思学院|ANOVA方差分析是什么?如何用EXCEL进行计算?
在数据分析、六西格玛管理领域中,ANOVA(方差分析)是一种基本的统计工具,广泛用于确定三组或三组以上的独立群体之间的平均值是否存在统计学上的显着差异。ANOVA的主要目的在于评估一个或多个因素的影响,通过比较不同样…...

Mindspore框架循环神经网络RNN模型实现情感分类|(三)RNN模型构建
Mindspore框架循环神经网络RNN模型实现情感分类 Mindspore框架循环神经网络RNN模型实现情感分类|(一)IMDB影评数据集准备 Mindspore框架循环神经网络RNN模型实现情感分类|(二)预训练词向量 Mindspore框架循环神经网络RNN模型实现…...

深度解读大语言模型中的Transformer架构
一、Transformer的诞生背景 传统的循环神经网络(RNN)和长短期记忆网络(LSTM)在处理自然语言时存在诸多局限性。RNN 由于其递归的结构,在处理长序列时容易出现梯度消失和梯度爆炸的问题。这导致模型难以捕捉长距离的依…...

安装好anaconda,打开jupyter notebook,新建 报500错
解决办法: 打开anaconda prompt 输入 jupyter --version 重新进入jupyter notebook: 可以成功进入进行代码编辑...

C++20之设计模式:状态模式
状态模式 状态模式状态驱动的状态机手工状态机Boost.MSM 中的状态机总结 状态模式 我必须承认:我的行为是由我的状态支配的。如果我没有足够的睡眠,我会有点累。如果我喝了酒,我就不会开车了。所有这些都是状态(states),它们支配着我的行为:…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...




