求最大公约数和最小公倍数---辗转相除法(欧几里得算法)
目录
一.GCD和LCM
1.最大公约数
2.最小公倍数
二.暴力求解
1.最大公约数
2.最小公倍数
三.辗转相除法
1.最大公约数
2.最小公倍数
一.GCD和LCM
1.最大公约数
最大公约数(Greatest Common Divisor,简称GCD)指的是两个或多个整数共有的约数中最大的一个数。例如,整数12和30的约数有1、2、3、6,但其中最大的约数是6,因此12和30的最大公约数是6。
最大公约数在数学中有着广泛的应用,例如可以用于简化分数、判断两个数是否互质、求解线性方程等。
特殊的gcd(0,n)为n,n为任意数
2.最小公倍数
最小公倍数(Least common multiple , 简称LCM)是两个或多个整数中最小的能够被这些整数整除的正整数。换句话说,最小公倍数是这些整数的公共倍数中最小的一个。
例如,整数 6 和 8 的公共倍数包括 24、48、72 等,其中 24 是最小的一个,因此它们的最小公倍数是 24。
最小公倍数在数学和计算中经常使用,例如在分数的约分和通分、整数的约数分解、最简分式的求解等方面。
无法求0和一个数的最小公倍数
最小公倍数(LCM)=num1*num2/最大公倍数(GCD)
二.暴力求解
1.最大公约数
思路:考虑特殊情况,当num1和num2一个为0,返回另一个的值.
两个数的最大公约数,一定不可能在(min(num1,num2),max(num1,num2)]之间因为两者之中较小者的最大约数为本身,所以我们选择从较小者开始遍历,当都可以整除(也就是求余等于0)的时候,说明找到了最大公约数.
public static int gcd(int num1, int num2) {if(num1==0)return num2;if(num2==0)return num1;int min = num1 < num2 ? num1 : num2;for (; min >= 1; --min) {if (num1 % min == 0 && num2 % min == 0) {return min;}}return min;}2.最小公倍数
思路:
两个数的最小公倍数,一定不可能在[0,max(num1,num2))之间因为两者之中较大者的最大倍数为本身,所以我们选择从较大者开始遍历,当都可以被整除(也就是求余等于0)的时候,说明找到了最小公倍数.
public static int lcm(int num1, int num2) {int max = num1 > num2 ? num1 : num2;for (; max <= num1 * num2; ++max) {if (max%num1==0&&max%num2==0) {return max;}}return max;}三.辗转相除法
辗转相除法,又称欧几里得算法或辗转相减法,是一种求最大公约数(Greatest Common Divisor,简称GCD)的算法。
假设要求两个正整数a和b的最大公约数,辗转相除法的步骤如下:
- 用a除以b,得到余数r;
- 如果r等于0,那么b就是最大公约数;
- 如果r不等于0,那么用b除以r,得到余数r1;
- 如果r1等于0,那么r就是最大公约数;
- 如果r1不等于0,那么继续用r除以r1,得到余数r2,以此类推,直到余数为0为止。
举个例子,假设要求36和24的最大公约数,辗转相除法的步骤如下:
36 ÷ 24 = 1 ... 12
24 ÷ 12 = 2 ... 0
因此,36和24的最大公约数是12。
辗转相除法的时间复杂度为O(logn),其中n为a和b中较大的那个数的位数。因此,辗转相除法是一种高效的求最大公约数的方法,被广泛应用于计算机科学和数学领域。
1.最大公约数
1.递归方法求解
//递归求解public static int gcd(int num1, int num2) {if (num2 == 0)return num1;return gcd(num2, num1 % num2);}2.迭代方法求解
//迭代求解public static int gcd(int num1, int num2) {int c = num1 % num2;while (c != 0) {num1 = num2;num2 = c;c = num1 % num2;}return num2;}2.最小公倍数
最小公倍数(LCM)=num1*num2/最大公倍数(GCD)
public static int lcm(int num1, int num2) {int x = num1, y = num2;int c = num1 % num2;while (c != 0) {num1 = num2;num2 = c;c = num1 % num2;}return x * y / num2;}相关文章:
)
求最大公约数和最小公倍数---辗转相除法(欧几里得算法)
目录 一.GCD和LCM 1.最大公约数 2.最小公倍数 二.暴力求解 1.最大公约数 2.最小公倍数 三.辗转相除法 1.最大公约数 2.最小公倍数 一.GCD和LCM 1.最大公约数 最大公约数(Greatest Common Divisor,简称GCD)指的是两个或多个整数共有…...
音视频开发_获取媒体文件的详细信息
一、前言 做音视频开发过程中,经常需要获取媒体文件的详细信息。 比如:获取视频文件的总时间、帧率、尺寸、码率等等信息。 获取音频文件的的总时间、帧率、码率,声道等信息。 这篇文章贴出2个我封装好的函数,直接调用就能获取媒体信息返回,copy过去就能使用,非常方便。…...
Springboot集成Swagger
一、Swagger简介注意点! 在正式发布的时候要关闭swagger(出于安全考虑,而且节省内存空间)之前开发的时候,前端只用管理静态页面, http请求到后端, 模板引擎JSP,故后端是主力如今是前…...

Vue全新一代状态管理库 Pinia【一篇通】
文章目录前言1. Pinia 是什么?1.1 为什么取名叫 Pinia?1.2. 为什么要使用 Pinia ?2. 安装 Pinia2.1.创建 Store2.1.1. Option 类型 Store2.1.2 Setup 函数类型 Store2.1.3 模板中使用3. State 的使用事项(Option Store )3.1 读取 State3.2 …...

STM32 -4 关于STM32的RAM、ROM
一 stm32 的flash是什么、有什么用、注意事项、如何查看 一 、说明 它主要用于存储代码,FLASH 存储器的内容在掉电后不会丢失,STM32 芯片在运行的时候,也能对自身的内部 FLASH 进行读写,因此,若内部 FLASH 存储了应用…...
第一个 Qt 程序
第一个 Qt 程序 “hello world ”的起源要追溯到 1972 年,贝尔实验室著名研究员 Brian Kernighan 在撰写 “B 语言教程与指导(Tutorial Introduction to the Language B)”时初次使用(程序),这是目前已 知最早的在计算机著作中将…...
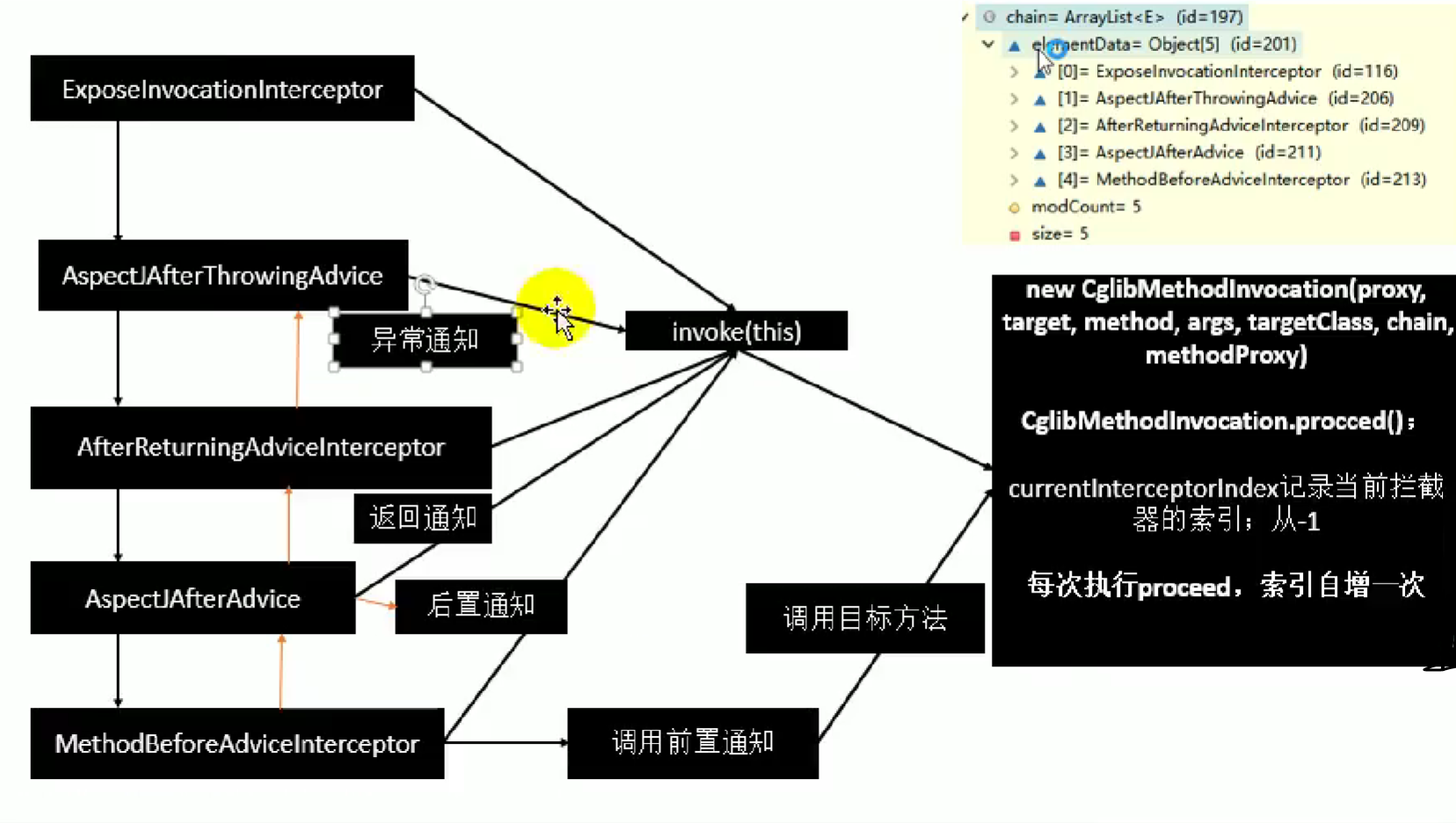
Spring注解驱动开发--AOP底层原理
Spring注解驱动开发–AOP底层原理 21. AOP-AOP功能测试 AOP:【动态代理】 指在程序运行期间动态的将某段代码切入到指定方法指定位置进行运行的编程方式; 1、导入aop模块:Spring AOP,(Spring-aspects) 2、定义一个业务逻辑类(Ma…...

对象的动态创建和销毁以及对象的复制,赋值
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才…...
JVM调优,调的是什么?目的是什么?
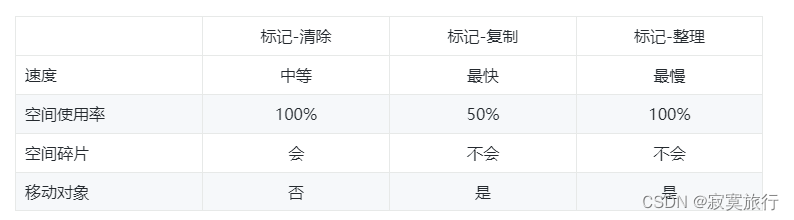
文章目录前言一、jvm是如何运行代码的?二、jvm的内存模型1 整体内存模型结构图2 堆中的年代区域划分3 对象在内存模型中是如何流转的?4 什么是FULL GC,STW? 为什么会发生FULL GC?5 要调优,首先要知道有哪些垃圾收集器及哪些算法6 调优不是盲目的,要有依据,几款内…...
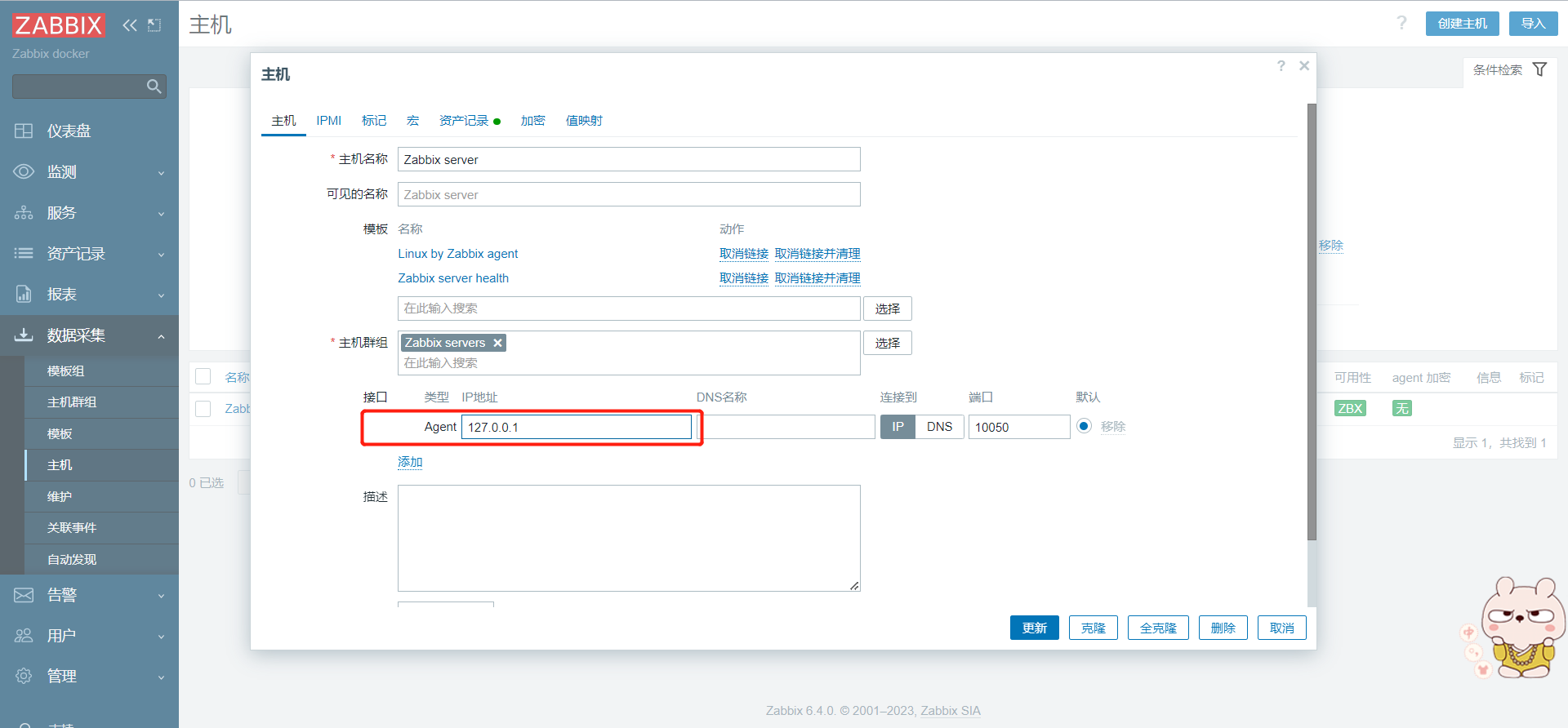
docker部署zabbix监控
docker部署zabbix监控 1、环境说明 公有云ubuntu22.04 系统->部署docker环境zabbix-server 6.4 2、准备docker环境 更新apt以及安装一些必要的系统工具 sudo apt-get update sudo apt-get -y install apt-transport-https ca-certificates curl software-properties-co…...

C语言刷题(6)(猜名次)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰还是在复习噢,今天来给大家介绍一个有意思的题目 题目名称: 猜名次 题目内容: 5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果: A选…...

两年外包生涯,感觉自己废了一半....
先说一下自己的情况。大专生,17年通过校招进入湖南某软件公司,干了接近2年的点点点,今年年上旬,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了五年的功能测试…...

【python】喜欢XJJ?这不得来一波大采集?
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 俗话说的好:技能学了~就要用在自己喜欢得东西上!! 这我不得听个话~我喜欢小姐姐,跳舞的小姐姐 这不得用python把小姐姐舞采集下来~嘿嘿嘿 完整源码、素材皆可点击文章下方名片…...

公司测试员用例写得乱七八糟,测试总监制定了这份《测试用例编写规范》
统一测试用例编写的规范,为测试设计人员提供测试用例编写的指导,提高编写的测试用例的可读性,可执行性、合理性。为测试执行人员更好执行测试,提高测试效率,最终提高公司整个产品的质量。 一、范围 适用于集成测试用…...
LeetCode 热题 HOT 100【题型归类汇总,助力刷题】
介绍 对于算法题,按题型类别刷题才会更有成效,因此我这里在网上搜索并参考了下 “🔥 LeetCode 热题 HOT 100” 的题型归类,并在其基础上做了一定的完善,希望能够记录自己的刷题历程,有所收获!具…...
【Java进阶篇】—— File类与IO流
一、File类的使用 1.1 概述 File 类以及本章中的各种流都定义在 java.io 包下 一个File对象代表硬盘或网络中可能存在的一个文件或文件夹(文件目录) File 能新建、删除、重命名 文件和目录,但 File不能访问文件内容本身。如果我们想要访问…...

Mysql 竟然还有这么多不为人知的查询优化技巧,还不看看?
前言 Mysql 我随手造200W条数据,给你们讲讲分页优化 MySql 索引失效、回表解析 今天再聊聊一些我想分享的查询优化相关点。 正文 准备模拟数据。 首先是一张 test_orde 表: CREATE TABLE test_order (id INT(11) NOT NULL AUTO_INCREMENT,p_sn VARCHA…...
 (附MATLAB和python代码实现))
MATLAB算法实战应用案例精讲-【智能优化算法】海洋捕食者算法(MPA) (附MATLAB和python代码实现)
目录 前言 知识储备 Lvy 飞行 布朗运动 算法原理 算法思想 数学模型...

Spring @Profile
1. Overview In this tutorial, we’ll focus on introducing Profiles in Spring. Profiles are a core feature of the framework — allowing us to map our beans to different profiles — for example, dev, test, and prod. We can then activate different profiles…...

Vue3电商项目实战-个人中心模块4【09-订单管理-列表渲染、10-订单管理-条件查询】
文章目录09-订单管理-列表渲染10-订单管理-条件查询09-订单管理-列表渲染 目的:完成订单列表默认渲染。 大致步骤: 定义API接口函数抽取单条订单组件获取数据进行渲染 落的代码: 1.获取订单列表API借口 /*** 查询订单列表* param {Number…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
