数据结构中的八大金刚--------八大排序算法
目录
引言
一:InsertSort(直接插入排序)
二:ShellSort(希尔排序)
三:BubbleSort(冒泡排序)
四: HeapSort(堆排序)
五:SelectSort(直接选择排序)
六:QuickSort(快速排序)
1.Hoare版本
2.前后指针版本
3.非递归版本
4.快排之三路划分
5.SGI-IntrospectiveSort(自省排序)
七:MergeSort(归并排序)
1.递归版本
2.非递归版本
八:CountSort(计数排序)

接下来的日子会顺顺利利,万事胜意,生活明朗-----------林辞忧
引言
在日常生活当中任何地方都有着排序的思想,对于网购时价格排序,销量排序,好评排序等各种排名,因此对于学习排序算法是很重要,对于排序算法有常见的八种,它们分别是 InsertSort(直接插入排序) ShellSort(希尔排序) BubbleSort(冒泡排序) HeapSort(堆排序) SelectSort(直接选择排序) QuickSort(快速排序) MergeSort(归并排序) CountSort(计数排序) 对于其他的如桶排序,奇数排序等实际用处不大,很少使用。接下来就介绍这八种排序算法
一:InsertSort(直接插入排序)
1.动图

2.思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
void InsertSort(int* a, int n)
{//[0,end]有序,插入a[end+1]for (int i = 0; i < n - 1; ++i){int end=i;int tmp = a[end + 1];while (end>=0){if (a[end] > tmp){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}3.时间复杂度:O(N^2) 最坏情况是逆序,最好情况是有序或者接近有序O(N)
二:ShellSort(希尔排序)
1.图片演示

2.思想:
当gap==1时为直接插入排序
间隔为gap的分为一组,总共gap组
int gap = 3;
for (int i = 0; i < n - gap; i += gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}再对gap组都进行排序
int gap = 3;
for (int j = 0; j < gap; ++j)
{for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}这样就完成了预排序,但如果对于数据量大的情况下,不止会进行一次预排序且还要控制最后一次预排序的gap==1这样就可以直接排序完成
int gap = n;
while (gap > 1)
{gap = gap / 3 + 1;for (int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}对于这里可以优化掉一层循环变为
void ShellSort(int* a, int n)
{//当gap>1时为预排序,目的是为了接近有序//当gap==1时为直接插入排序//间隔为gap的分为一组,总共gap组int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}以前的是一组排序完了再排下一组,这里是全部gap组一次排过去
3.关于gap如何取的问题以及一些其他注意问题
时间复杂度:O(N^1.3)

三:BubbleSort(冒泡排序)
1.动图展示

2. 代码实现
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int exchange = 0;for (int j = 0; j < n - 1 - i; ++j){if (a[j] > a[j + 1]){Swap(&a[j],&a[j+1]);exchange = 1;}}if (exchange == 0){break;}}
}3.时间复杂度O(N^2)
详细介绍可参考https://blog.csdn.net/Miwll/article/details/135315155?spm=1001.2014.3001.5501
四: HeapSort(堆排序)
1.图片展示

2.思想及代码实现
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] < a[child + 1]){++child;}if (a[parent] < a[child]){Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{//排升序建大根堆--向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}//排数据--首尾交换再向下调整int end = n - 1;while (end){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}
}时间复杂度为O(N*logN)
详细可以参考https://blog.csdn.net/Miwll/article/details/136636869?spm=1001.2014.3001.5501
五:SelectSort(直接选择排序)
1.动图显示

2.思想及实现
void SelectSort(int* a, int n)
{//遍历一遍选出最大和最小值下标,再收尾交换int begin = 0, end = n - 1;int maxi = 0, mini = 0;while (begin < end){for (int i = begin; i <= end; ++i){if (a[i] > a[maxi]) maxi = i;if (a[i] < a[mini]) mini = i;}Swap(&a[begin], &a[mini]);if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}
}这里需要注意当begin和maxi重叠的情况

时间复杂度:O(N^2)
六:QuickSort(快速排序)
1.Hoare版本
1.动图展示

2.思想及实现
对于Hoare版本的快排是选取一个key值,然后先让右边先走找小,再左边找大,再交换继续往后直至相遇,再交换key位置处的值,再以相遇位置为划分子区间继续执行


画一部分递归展开图理解最小子问题的条件

3.为啥相遇位置一定比key值小?---右边先走保证的

4.快排的时间复杂度为O(N*logN),但在有序或者接近有序的情况下最坏为O(N^2),为了防止出现最坏的情况,可以使用三数取中或者随机选key来解决问题

//2.三数取中
int mid = GetMidi(a,begin, end);
Swap(&a[begin], &a[mid]);int GetMidi(int*a,int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[right] > a[mid])//mid>left right>mid{return mid;}else if (a[left] > a[right])//mid>left right<mid{return left;}else{return right;}}else //left>mid{if (a[right] < a[mid])//right<mid{return mid;}else if (a[left] > a[right])//right>mid {return right;}else{return left;}}
}5.小区间优化 由于到最后的几步时,递归的深度和广度是非常巨大的,因此可以采用小区间优化的方式减少递归,这里可以采用插入排序
void QuickSort1(int* a, int begin, int end)
{//最小子问题--区间不存在或者只有一个数据if (begin >= end) return;//1.随机选key---选[left, right]区间中的随机数做key//int randi = rand() % (end - begin + 1);//randi += begin;//在递归时begin不一定是0开始的//Swap(&a[begin],&a[randi]);if (end - begin + 1 < 10){InsertSort(a+begin, end - begin + 1);}else{//2.三数取中int mid = GetMidi(a, begin, end);Swap(&a[begin], &a[mid]);int keyi = begin;int left = begin, right = end;while (left < right)//相遇时就停止{//先让右边走while (left < right && a[right] >= a[keyi]){--right;}//再左边走while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;//[begin,keyi-1] keyi [keyi+1,end]QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}
}2.前后指针版本
1.动图展示

2.思想及实现
当cur处的值>=key时,++cur
当cur处的值<key时,++prev,再交换prev和cur的值,再++cur
void QuickSort2(int* a, int begin, int end)
{if (begin >= end) return;int prev = begin;int cur = begin + 1;int keyi = begin;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev],&a[cur]);}++cur;}Swap(&a[prev],&a[keyi]);keyi = prev;//[begin,keyi-1]keyi[keyi+1,end]QuickSort2(a, begin, keyi - 1);QuickSort2(a, keyi + 1, end);
}3.非递归版本
对于递归如果深度太深的话,就会导致栈溢出,因此用栈实现非递归版本很重要
思想:走一趟单趟,再右左区间入栈
void QuickSortNonR(int* a, int begin, int end)
{ST st;STInit(&st);//先入右再入左STPush(&st, end);STPush(&st, begin);while (!STEmpty(&st)){int left = STTop(&st);STPop(&st);int right = STTop(&st);STPop(&st);//单趟int keyi = left;int cur = left + 1;int prev = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur],&a[prev]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;//[left,keyi-1]keyi[keyi+1,right]//保证入的区间有效if (keyi + 1 < right){STPush(&st, right);STPush(&st, keyi + 1);}if (left < keyi -1){STPush(&st, keyi - 1);STPush(&st, left);}//Print(a, left, right);}STDestroy(&st);
}4.快排之三路划分
1.快排性能的关键点分析
决定快排性能的关键点是每次单趟排序后,key对数组的分割,如果每次选key基本⼆分居中,那么快 排的递归树就是颗均匀的满⼆叉树,性能最佳。但是实践中虽然不可能每次都是⼆分居中,但是性能 也还是可控的。但是如果出现每次选到最⼩值/最⼤值,划分为0个和N-1的⼦问题时,时间复杂度为 O(N^2),数组序列有序时就会出现这样的问题,我们前⾯已经⽤三数取中或者随机选key解决了这个问 题,也就是说我们解决了绝⼤多数的问题,但是现在还是有⼀些场景没解决(数组中有⼤量重复数据时),即以下情况

此时就提出了采用三路划分的思想来解决


这样再对比key大的数据区间和比key小的数据区间进行递归
//三路划分
void QuickSort3(int* a, int begin, int end)
{//最小子问题if (begin >= end) return;int left = begin, right = end;int key = a[left];int cur = left + 1;while (cur <= right){if (a[cur] < key){Swap(&a[left], &a[cur]);++cur;++left;}else if(a[cur]>key){Swap(&a[cur],&a[right]);--right;}else{++cur;}}//[begin,left-1][left,right][right+1,end]QuickSort3(a, begin, left - 1);QuickSort3(a, right+1, end);
}5.SGI-IntrospectiveSort(自省排序)
introsort是introspectivesort采⽤了缩写,他的名字其实表达了他的实现思路,他的思路就是进⾏⾃ 我侦测和反省,快排递归深度太深(sgistl中使⽤的是深度为2倍排序元素数量的对数值)那就说明在 这种数据序列下,选key出现了问题,性能在快速退化,那么就不要再进⾏快排分割递归了,改换为堆 排序进⾏排序
void IntroSort(int* a, int left, int right, int depth, int defaultDepth)
{if (left >= right)return;// 数组长度⼩于16的⼩数组,换为插入排序,简单递归次数---小区间优化 if (right - left + 1 < 16){InsertSort(a + left, right - left + 1);return;}// 当深度超过2 * logN时改用堆排序 if (depth > defaultDepth){HeapSort(a + left, right - left + 1);return;}depth++;int begin = left;int end = right;// 随机选keyint randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end]IntroSort(a, begin, keyi - 1, depth, defaultDepth);IntroSort(a, keyi + 1, end, depth, defaultDepth);
}void QuickSort4(int* a, int begin, int end)
{int depth = 0;int logn = 0;int N= end - begin + 1;for (int i = 1; i < N; i *= 2){logn++;}// introspective sort -- 自省排序IntroSort(a, begin, end, depth, logn * 2);
}七:MergeSort(归并排序)
1.递归版本
1.动图演示

2.思想及实现

void _MergeSort(int* a, int left,int right,int*tmp)
{//最小子问题if (left == right) return;int mid = (left + right) / 2;//[begin,mid][mid+1,end]_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);//开始归并int begin1 = left, end1=mid;int begin2=mid+1, end2=right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right-left+1));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}部分递归展开

2.非递归版本
这里的非递归版本采用循环的方式来解决

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = begin1 + gap - 1;int begin2 = end1 + 1, end2 = begin2 + gap - 1;//调整越界问题if (end1 >= n || begin2 >= n){break;}if (end2 >= n)//修正{end2 = n - 1;}int j = i;while (begin1 <= end1 && begin2 <= end2){//取小的尾插if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));}gap *= 2;}
}八:CountSort(计数排序)
1.思想及实现
开辟一个数组用来统计每个数据出现的次数,在相对映射位置的次数++,然后再往原数组写入数据,适合于整形且数据集中的
void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 1; i < n; ++i){if (min > a[i]) min = a[i];if (max < a[i]) max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail\n");return;}memset(count, 0, sizeof(int) * range);//统计次数for (int i = 0; i < n; ++i){count[a[i] - min]++;}//写回原数组int j = 0;for (int i = 0; i < range; ++i){while (count[i]--){a[j++] = i + min;}}
}总结

相关文章:

数据结构中的八大金刚--------八大排序算法
目录 引言 一:InsertSort(直接插入排序) 二:ShellSort(希尔排序) 三:BubbleSort(冒泡排序) 四: HeapSort(堆排序) 五:SelectSort(直接选择排序) 六:QuickSort(快速排序) 1.Hoare版本 2.前后指针版本 …...

ACC2.【C语言】经验积累 栈区简单剖析
int main() {int i0;int arr[10]{1,2,3,4,5,6,7,8,9,10};for (i0;i<12;i){arr[i]0;printf("A");}return 0; } 执行后无限打印A 在VS2022,X86,Debug环境下,用监视后,原因是arr[12]的地址与i的地址重合(数组越界&…...

c# 索引器
索引器(Indexer)允许你像访问数组一样,通过索引访问对象的属性或数据。索引器的主要用途是在对象内部封装复杂的数据结构,使得数据访问更加直观。下面是关于 C# 索引器的详细解释及示例: 基本语法 索引器的语法类似于…...

低代码如何加速数字化转型
数字化转型,正日益决定企业成功的关键。这里的一个关键因素是它可以以更快的速度和质量来实施技术计划。在当今瞬息万变的商业环境中,战略性地采用低代码平台对于旨在加快上市时间、增强业务敏捷性和促进跨团队无缝协作的首席技术官来说至关重要。日益增…...

Pytest进阶之fixture的使用(超详细)
目录 Fixture定义 Fixture使用方式 作为参数使用 Fixture间相互调用(作为参数调用) 作为conftest.py文件传入 Fixture作用范围Scope function class module session Fixture中params和ids Fixture中autouse Fixture中Name 总结 pytest fixture 是一种用来管理测试…...

GitHub 详解教程
1. 引言 GitHub 是一个用于版本控制和协作的代码托管平台,基于 Git 构建。它提供了强大的功能,使开发者可以轻松管理代码、追踪问题、进行代码审查和协作开发。 2. Git 与 GitHub 的区别 Git 是一个分布式版本控制系统,用于跟踪文件的更改…...

边界网关IPSEC VPN实验
拓扑: 实验要求:通过IPSEC VPN能够使PC2通过网络访问PC3 将整个路线分为三段 IPSEC配置在FW1和FW2上,在FW1与FW2之间建立隧道,能够传递IKE(UDP500)和ESP数据包,然后在FW1与PC2之间能够流通数据…...

力扣高频SQL 50题(基础版)第六题
文章目录 1378. 使用唯一标识码替换员工ID题目说明思路分析实现过程结果截图总结 1378. 使用唯一标识码替换员工ID 题目说明 Employees 表: ---------------------- | Column Name | Type | ---------------------- | id | int | | name | varchar | ------…...

在一个事物方法中开启新事物,完成对数据库的修改
在Java中,使用Transactional注解来管理事务非常常见。但是,在一个已经标记为Transactional的方法内部调用另一个也标记了Transactional的方法时,如果不正确处理,可能会导致一些意料之外的行为。这是因为默认情况下,Spr…...

ffmpeg的vignetting filter
vignetting filter是暗角过滤器 vignetting filter在官网是vignette。但是我查了一下,vignetting应该是正确的表达,vignette是什么鬼? 官网参数 官书参数 参数解释 angle,x0,y0可以使用表达式。 angle:不知道什么意思…...

商场导航系统:从电子地图到AR导航,提升顾客体验与运营效率的智能解决方案
商场是集娱乐、休闲、社交于一体的综合性消费空间,随着商场规模的不断扩大和布局的日益复杂,顾客在享受丰富选择的同时,也面临着寻路难、店铺曝光率低以及商场管理效率低下等挑战。商场导航系统作为提升购物体验的关键因素,其重要…...

vue3中父子组件的双向绑定defineModel详细使用方法
文章目录 一、defineProps() 和 defineEmits()二、defineModel() 的双向绑定2.1、基础示例2.2、定义类型2.3、声明prop名称2.4、其他声明2.5、绑定多个值2.6、修饰符和转换器2.7、修饰符串联 一、defineProps() 和 defineEmits() 组件之间通讯,通过 props 和 emits…...

耳机、音响UWB传输数据模组,飞睿智能低延迟、高速率超宽带uwb模块技术音频应用
在数字化浪潮席卷全球的今天,无线通信技术日新月异,其中超宽带(Ultra-Wideband,简称UWB)技术以其独特的优势,正逐步成为无线传输领域的新星。本文将深入探讨飞睿智能UWB传输数据模组在音频应用中的创新应用…...

webpack配置报错:Invalid options object.
前言: 今天在使用webpack进行项目配置的时候,运行之后终端报错:Invalid options object. Dev Server has been initialized using an options object that does not match the API schema. - options has an unknown property inline. Thes…...
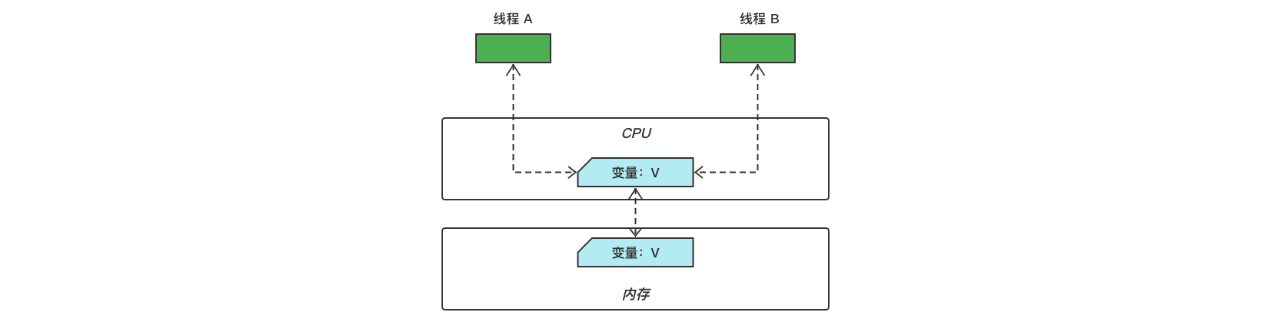
Java 并发编程:一文了解 Java 内存模型(处理器优化、指令重排序与内存屏障的深层解析)
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 022 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

谷粒商城实战笔记-64-商品服务-API-品牌管理-OSS前后联调测试上传
文章目录 1,拷贝文件到前端工程2,局部修改3,在品牌编辑界面使用上传组件4,OSS配置允许跨域5,测试multiUpload.vue完整代码singleUpload.vue完整代码policy.js代码 在Web应用开发中,文件上传是一项非常常见的…...

Springboot 开发之 RestTemplate 简介
一、什么是RestTemplate RestTemplate 是Spring框架提供的一个用于应用中调用REST服务的类。它简化了与HTTP服务的通信,统一了RESTFul的标准,并封装了HTTP连接,我们只需要传入URL及其返回值类型即可。RestTemplate的设计原则与许多其他Sprin…...

Django transaction.atomic()事务处理
在Django中,transaction.atomic()是一个上下文管理器,它会自动开始一个事务,并在代码块执行完毕后提交事务。如果在代码块中抛出异常,事务将被自动回滚,确保数据库的一致性和完整性。 在实际应用中,你可能需…...
)
2024.07-电视版免费影视App推荐和猫影视catvod、TVBox源(最新接口地址)
文章目录 电视版免费影视App推荐精选列表(2024.07可用筛选列表):2024.07可用筛选列表,盲盒资源打包合集下载安装说明真的是盲盒? 猫影视catvod、TVBoxTVBox源推荐可用列表目前不可用列表(前缀为错误状态码&…...

【Python】 基于Q-learning 强化学习的贪吃蛇游戏(源码+论文)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
