美团后端二面
美团后端二面
………………………………
两道场景
一道 数字转中文读法(1000-》一千)
0八股0自我介绍
反问 “您觉得我能过吗?” “这个需要横行对比之后才能有结果”
………………………………
什么时候到岗
场景题 1
假设我有一个文本文件。这个文本文件每一行都是一个长度不固定的,由英文字符跟阿拉伯数字组成的字符串。但是它的长度不固定。就是文件也比较大。我现在需要您在内存有限的情况下去统计出这个文本文件当中出现次数最多的5个字符串。
分治
分小文件hash ,然后每个取top5,然后总的取top5
………………………………
场景题 2
比如说我们现在在搞一个大促对吧?我们现在在卖商品,然后商品卖商品通常都会有一个这样的一个功能,就是榜单。就是说我们每卖一件商品,我往一个文件当中去写一个这个商品的
ID 对吧?然后商品的编码。然后我是进行大促的那一刻开始到当前我们卖的最好的100件商品的一个榜单。啊那这是一个实际的业务场景了。
一开始没答道点子上,面试官引导他没限制内存,
然后又引导 (在不影响业务的情况下,降低成本)
排行榜不需要很精准
排行榜需要尽快返回
面试官:其实我想问的是说如何尽量地节约成本
后面又提到pipeline的思想
不要一次一次传输,累计传输一下
编程精选网(www.codehuber.com),程序员的终身学习网站已上线!
如果这篇【文章】有帮助到你,希望可以给【JavaGPT】点个赞👍,创作不易,如果有对【后端技术】、【前端领域】感兴趣的小可爱,也欢迎关注❤️❤️❤️ 【JavaGPT】❤️❤️❤️,我将会给你带来巨大的【收获与惊喜】💝💝💝!
相关文章:

美团后端二面
美团后端二面 ……………………………… 两道场景 一道 数字转中文读法(1000-》一千) 0八股0自我介绍 反问 “您觉得我能过吗?” “这个需要横行对比之后才能有结果” ……………………………… 什么时候到岗 场景题 1 假设我有一个…...
:对C语言作用域规则 局部变量、全局变量的认识)
学懂C语言(十六):对C语言作用域规则 局部变量、全局变量的认识
一、C 作用域规则 任何一种编程中,作用域是程序中定义的变量所存在的区域,超过该区域变量就不能被访问。C 语言中有三个地方可以声明变量: 局部变量:在函数或块内部全局变量:在所有函数外部形式参数:在函数…...
的理论知识)
关于TS(typescript)的理论知识
关于TS(typescript)的理论知识 TypeScript 是一种由微软开发的开源编程语言,它是 JavaScript 的一个超集,添加了可选的静态类型和基于类的面向对象编程。TypeScript 最终会被编译成纯 JavaScript 代码,以便在任何支持 …...

【OpenCV C++20 学习笔记】基本图像容器——Mat
【OpenCV C20 学习笔记】基本图像容器——Mat 概述Mat内部结构引用计数机制颜色数据格式 显式创建Mat对象使用cv::Mat::Mat构造函数矩阵的数据项 使用数组进行初始化的构造函数cv::Mat::create函数MATLAB风格的初始化小型矩阵通过复制创建Mat对象 Mat对象的输出其他普通数据项的…...

枚举单例是怎么保证线程安全和防止反射的
枚举单例在Java中具有天然的线程安全性和防止反射攻击的特性,这是由于Java对枚举类型的特殊处理方式。以下是详细解释: 1. 线程安全性 Java 枚举类的特性 类加载机制:枚举类型在Java中是特殊的类,由JVM保证其线程安全性。枚举类…...

传知代码-智慧医疗:纹理特征VS卷积特征(论文复现)
代码以及视频讲解 本文所涉及所有资源均在传知代码平台可获取 论文链接:https://www.sciencedirect.com/science/article/abs/pii/S1076633223003537?__cf_chl_rt_tkJ9Aipfxyk5d.leu48P20ePFNd4B2aunaSmzVpXCg.7g-1721292386-0.0.1.1-6249 论文概述 今天我们把视线…...

数据结构中的八大金刚--------八大排序算法
目录 引言 一:InsertSort(直接插入排序) 二:ShellSort(希尔排序) 三:BubbleSort(冒泡排序) 四: HeapSort(堆排序) 五:SelectSort(直接选择排序) 六:QuickSort(快速排序) 1.Hoare版本 2.前后指针版本 …...

ACC2.【C语言】经验积累 栈区简单剖析
int main() {int i0;int arr[10]{1,2,3,4,5,6,7,8,9,10};for (i0;i<12;i){arr[i]0;printf("A");}return 0; } 执行后无限打印A 在VS2022,X86,Debug环境下,用监视后,原因是arr[12]的地址与i的地址重合(数组越界&…...

c# 索引器
索引器(Indexer)允许你像访问数组一样,通过索引访问对象的属性或数据。索引器的主要用途是在对象内部封装复杂的数据结构,使得数据访问更加直观。下面是关于 C# 索引器的详细解释及示例: 基本语法 索引器的语法类似于…...

低代码如何加速数字化转型
数字化转型,正日益决定企业成功的关键。这里的一个关键因素是它可以以更快的速度和质量来实施技术计划。在当今瞬息万变的商业环境中,战略性地采用低代码平台对于旨在加快上市时间、增强业务敏捷性和促进跨团队无缝协作的首席技术官来说至关重要。日益增…...

Pytest进阶之fixture的使用(超详细)
目录 Fixture定义 Fixture使用方式 作为参数使用 Fixture间相互调用(作为参数调用) 作为conftest.py文件传入 Fixture作用范围Scope function class module session Fixture中params和ids Fixture中autouse Fixture中Name 总结 pytest fixture 是一种用来管理测试…...

GitHub 详解教程
1. 引言 GitHub 是一个用于版本控制和协作的代码托管平台,基于 Git 构建。它提供了强大的功能,使开发者可以轻松管理代码、追踪问题、进行代码审查和协作开发。 2. Git 与 GitHub 的区别 Git 是一个分布式版本控制系统,用于跟踪文件的更改…...

边界网关IPSEC VPN实验
拓扑: 实验要求:通过IPSEC VPN能够使PC2通过网络访问PC3 将整个路线分为三段 IPSEC配置在FW1和FW2上,在FW1与FW2之间建立隧道,能够传递IKE(UDP500)和ESP数据包,然后在FW1与PC2之间能够流通数据…...

力扣高频SQL 50题(基础版)第六题
文章目录 1378. 使用唯一标识码替换员工ID题目说明思路分析实现过程结果截图总结 1378. 使用唯一标识码替换员工ID 题目说明 Employees 表: ---------------------- | Column Name | Type | ---------------------- | id | int | | name | varchar | ------…...

在一个事物方法中开启新事物,完成对数据库的修改
在Java中,使用Transactional注解来管理事务非常常见。但是,在一个已经标记为Transactional的方法内部调用另一个也标记了Transactional的方法时,如果不正确处理,可能会导致一些意料之外的行为。这是因为默认情况下,Spr…...

ffmpeg的vignetting filter
vignetting filter是暗角过滤器 vignetting filter在官网是vignette。但是我查了一下,vignetting应该是正确的表达,vignette是什么鬼? 官网参数 官书参数 参数解释 angle,x0,y0可以使用表达式。 angle:不知道什么意思…...

商场导航系统:从电子地图到AR导航,提升顾客体验与运营效率的智能解决方案
商场是集娱乐、休闲、社交于一体的综合性消费空间,随着商场规模的不断扩大和布局的日益复杂,顾客在享受丰富选择的同时,也面临着寻路难、店铺曝光率低以及商场管理效率低下等挑战。商场导航系统作为提升购物体验的关键因素,其重要…...

vue3中父子组件的双向绑定defineModel详细使用方法
文章目录 一、defineProps() 和 defineEmits()二、defineModel() 的双向绑定2.1、基础示例2.2、定义类型2.3、声明prop名称2.4、其他声明2.5、绑定多个值2.6、修饰符和转换器2.7、修饰符串联 一、defineProps() 和 defineEmits() 组件之间通讯,通过 props 和 emits…...

耳机、音响UWB传输数据模组,飞睿智能低延迟、高速率超宽带uwb模块技术音频应用
在数字化浪潮席卷全球的今天,无线通信技术日新月异,其中超宽带(Ultra-Wideband,简称UWB)技术以其独特的优势,正逐步成为无线传输领域的新星。本文将深入探讨飞睿智能UWB传输数据模组在音频应用中的创新应用…...

webpack配置报错:Invalid options object.
前言: 今天在使用webpack进行项目配置的时候,运行之后终端报错:Invalid options object. Dev Server has been initialized using an options object that does not match the API schema. - options has an unknown property inline. Thes…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
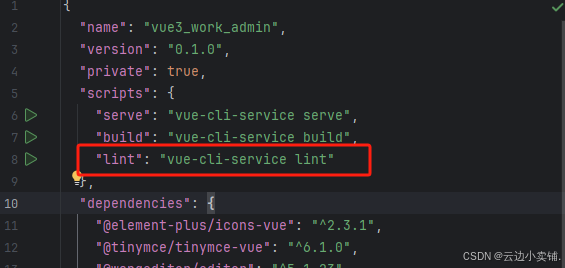
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

CppCon 2015 学习:Simple, Extensible Pattern Matching in C++14
什么是 Pattern Matching(模式匹配) ❝ 模式匹配就是一种“描述式”的写法,不需要你手动判断、提取数据,而是直接描述你希望的数据结构是什么样子,系统自动判断并提取。❞ 你给的定义拆解: ✴ Instead of …...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...
