字符串匹配【BF、KMP算法】
文章目录
- :star:BF算法
- 代码实现
- BF的改进思路
- :star:KMP算法
- 🚩next数组🚩
- 代码实现
- 优化next数组
- 最终代码
⭐️BF算法
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将主串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。
代码实现
int BF(const char* S, const char* P)
{assert(S && P);int i = 0;int j = 0;int lenS = strlen(S);int lenP = strlen(P);while (i < lenS && j < lenP){if (S[i] == P[j]){i++;j++;}else{i = i - j + 1;j = 0;}}if (j >= lenP){return i - j;}return -1;
}
return -1;
}BF的改进思路
在最坏的情况下,模式串只有最后一个字符和主串不一样
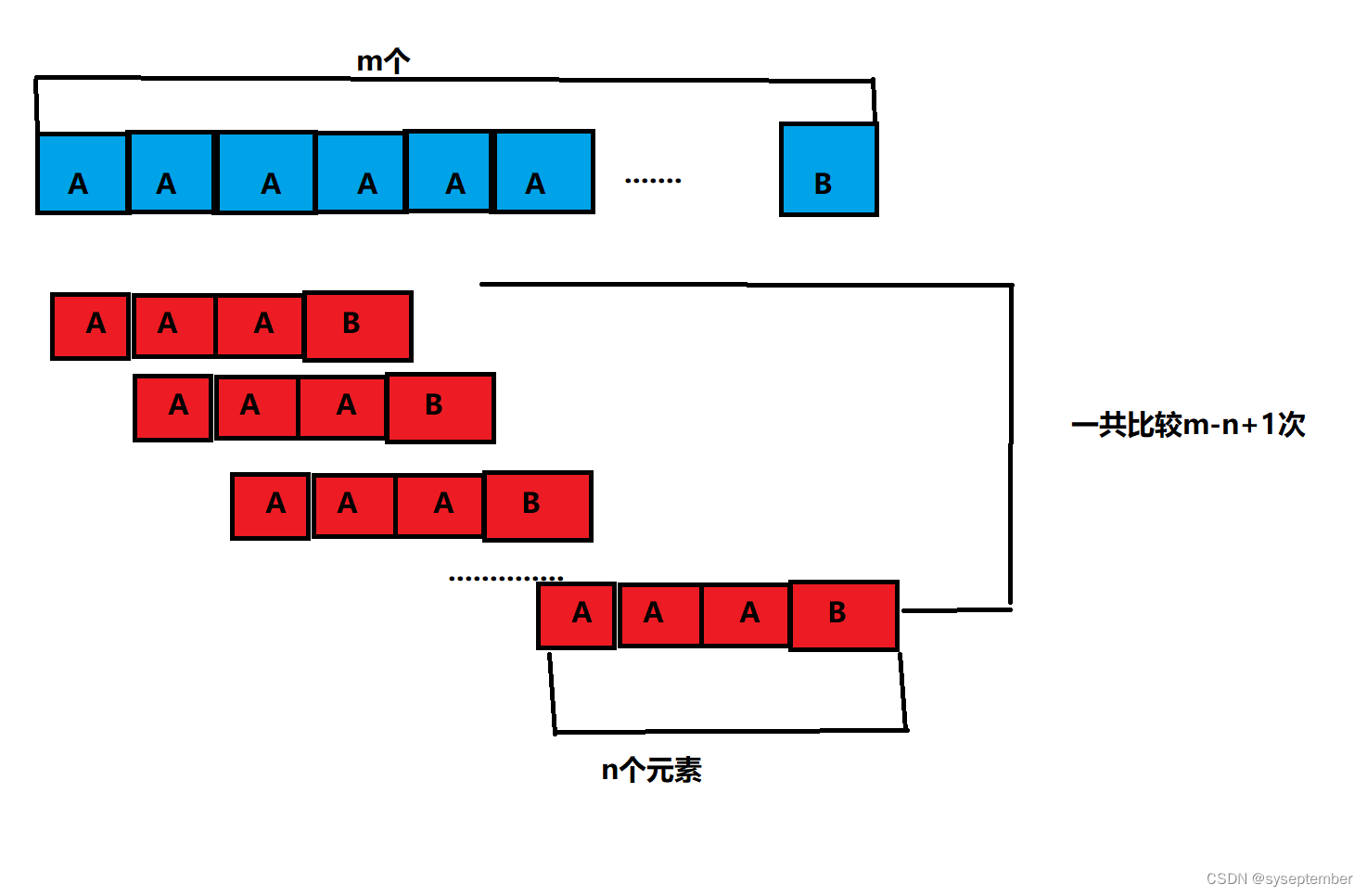
BF最坏的情况时间复杂度是O(mn),效率太低了
我们很难降低字符串比较的复杂度(因为比较两个字符串,真的只能逐个比较字符)。因此,我们考虑降低比较的趟数。如果比较的趟数能降到足够低,那么总的复杂度也将会下降很多。要优化一个算法,首先要回答的问题是“我手上有什么信息?” 我们手上的信息是否足够、是否有效,决定了我们能把算法优化到何种程度。请记住:尽可能利用残余的信息,是KMP算法的思想所在。
⭐️KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)
区别:KMP 和 BF 唯一不一样的地方在,主串的 str1 并不会回退,并且 str2 也不会移动到 0 号位置,而是移动到某一个特别位置
上面概念有点抽象,我们举一个具体例子
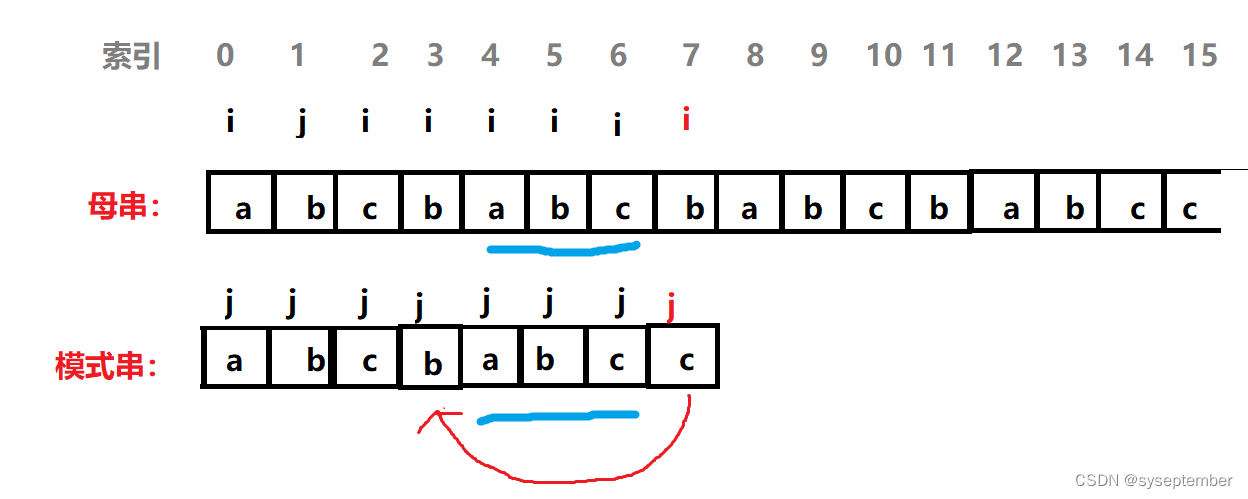
请记住:KMP算法和BF算法不同的是BF中发现匹配失败str1会回退到前一个位置的下一个位置,str2回退到模式串起始位置,KMP匹配失败后str1(i)不回退,str2(j)回退到某一个位置,这个位置可能是模式串的起始位置,也可能不是起始位置。
如果j想回退到某一个位置,这个位置应该满足这几个条件
- j回退的位置一定要尽可能靠近回退前的位置,这样可以保证后续循环的次数更少
- j回退的位置前面k个字符一定要和i前面k个字符相等
第二个原因是因为i是不动的,所以接下来想要从移动后的j继续向后匹配的前提就是i前面k个字符和移动后的j前面k个字符完全相同
我们将最终目的是寻找j的回退位置,现在我们已经知道了回退位置所需要满足的条件,根据第2个条件,我们可以推出j回退的位置前面k个字符和j回退前的k个字符相等
这是因为j回退后位置的前k个字符和i前k个字符相等,而i位置的前k个字符右和j回退前的前k个字符相等(因为i和j所指的位置前面全部是匹配的),所以我们能推出j回退后的位置前面k个字符与j回退前的位置前面k个字符相同(非常重要!!!我们就是通过这个条件来找到j的回退位置)
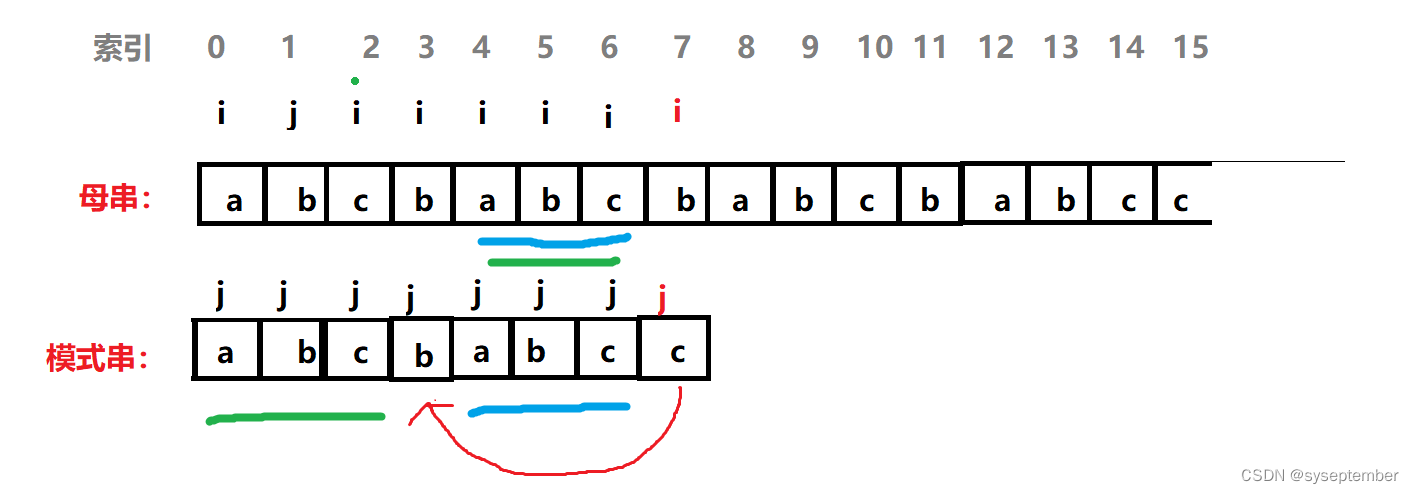
目前为止,我们将寻找j的回退位置这个问题转化成了一个寻找某个位置,这个位置前面k个字符和j回退前位置的前k个字符相等
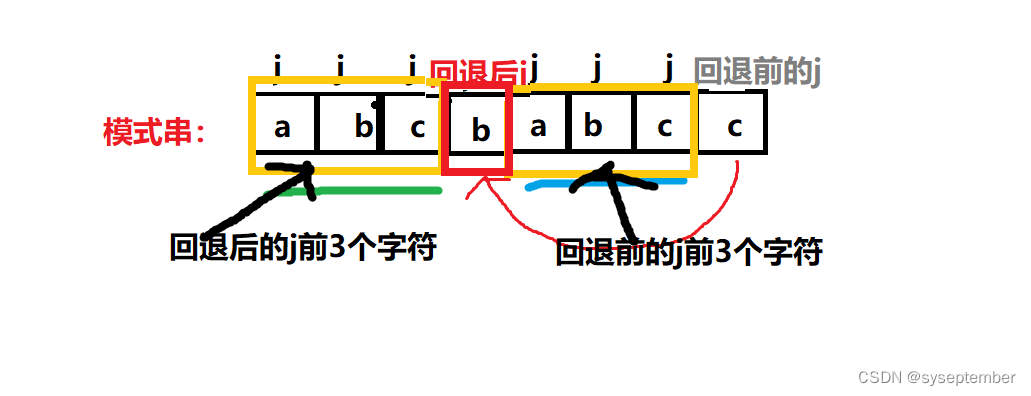
接下来,我们引入next数组,通过next数组我们就能知道j到底要回到到什么位置,请继续往下看
🚩next数组🚩
KMP 的精髓就是 next 数组:也就是用 next[j] = k;来表示,每一个模式串中的j对应一个 K 值,K就是j移动后的位置(next数组对应的是模式串,每一个模式串都有自己的next数组,并且next数组的元素个数等于模式串的长度)
如下是对next数组的定义
- next[0]一定是-1,next[1]一定是0
- 对于next[j],j>=2时,next[j]的值就是 模式串中下标为j的元素前面的k个元素与模式串中下标为0的元素后面k个元素完全相等的最大k值
举例:
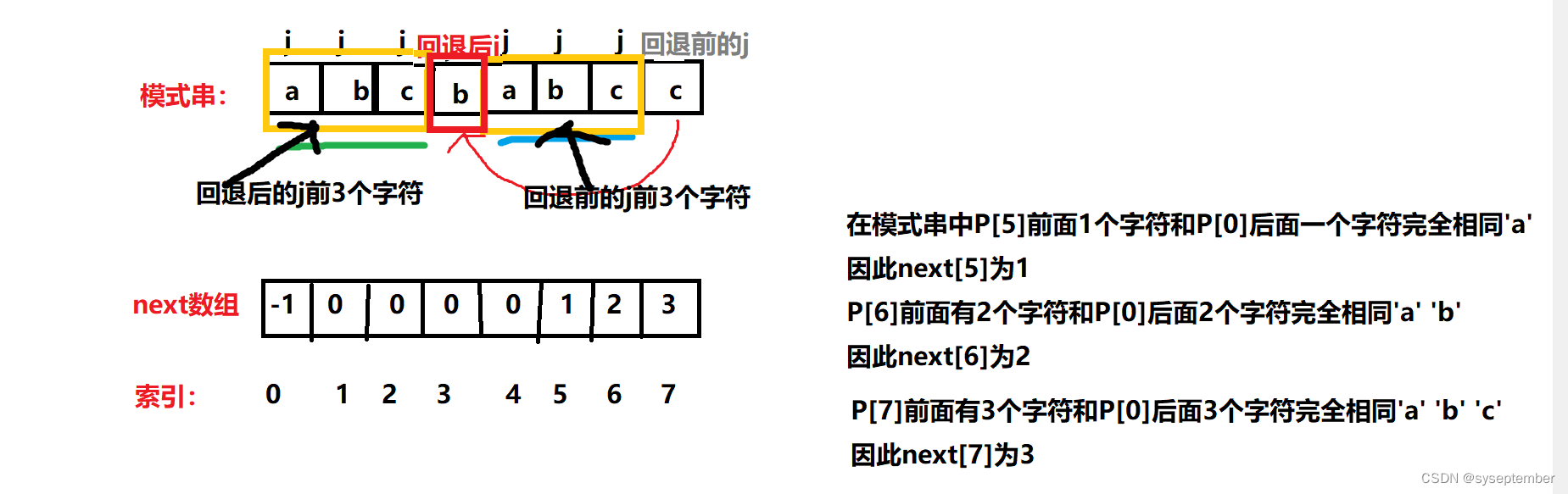
例如对于模式串"abcbabcc"
它的next数组是{-1, 0, 0, 0, 0, 1, 2, 3}
next数组的作用
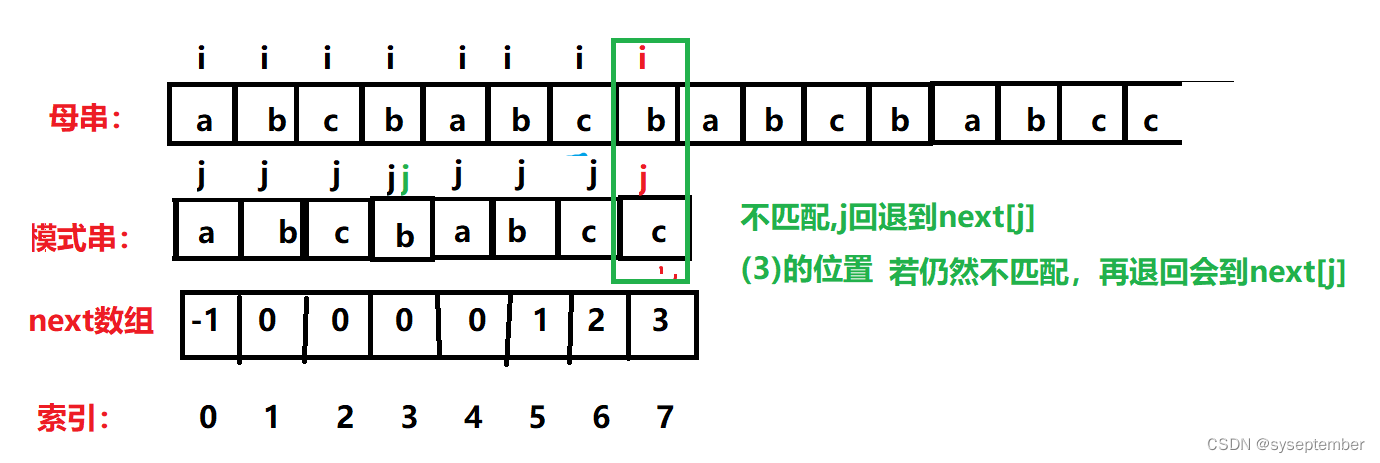
若i与j的位置不匹配,则j直接返回到next[j]的位置(再次判断i和j的位置是否匹配,仍然不匹配,继续退回到next[j]),因为根据next数组的定义,next[j]的值就是P[j]前k个元素与P[0]后k个元素相等的最大k值,而j返回到k的位置恰好可以保证此时j前面的k个元素和i前面的k个元素完全相同!!!
🚩next数组练习
练习 1: 举例对于”ababcabcdabcde”, 求其的 next 数组?
-1 0 0 1 2 0 1 2 0 0 1 2 0 0
练习 2: 再对”abcabcabcabcdabcde”,求其的 next 数组? "
-1 0 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 0
我们可以发现以下规律,如果next数组的值要增加,那么只能在之前的值上增加1,如果next数组的值要减小,可以一次减少多个数
🚩看到这里,我们来理一下我们的思路,首先:KMP算法和BF的算法本质就是KMP发现匹配失败后i的值不变,j回退到某一个位置;其次:我们分析了回退的位置需要满足一个条件(j回退后的位置前面k个字符和j回退前的k个字符相等)才有可能继续与主串匹配;现在:我们根据回退的位置需要满足的条件引出了next数组(next[j]的值就是模式串与主串补不匹配后j退回的位置),我们接下来要做的就是通过代码求出next数组,一但我们求出了next数组,我们就可以知道j回退的位置具体是哪里了j
🚩next数组的求解🚩
我们手写next数组很容易,因为我们用眼睛可以观察出P[j]前面K个元素和P[0]后面K个元素相同的最大K值,但是计算机无法观察出来,因此我们需要寻找规律
由next数组练习我们可以发现以下规律:如果next数组的值要增加,那么只能在之前的值上增加1,如果next数组的值要减小,可以一次减少多个数
- 证明如果要next数组的值要增加,只能在前一个的值上增加1
反证法证明:假设next[i]==k,next[j]==k+2(j>i并且中间没有元素等于k+1)
由next数组定义可知P[0]~P[k-1]==P[j-k]~P[j-1],P[0]~P[k+1]==P[j-k-2]~P[j+1],
则一定有P[k]==P[j],于是有P[0]~P[k]==P[j-k]~P[j]这说明了i和j中间一定有元素P[m]==k+1
与假设矛盾,因此推出如果next数组的值要增加,那么只能在之前的值上增加1- 如果要next数组的值要减少,可以减少多个数这点毋庸置疑,无需证明
求解next数组还差最后一步,什么时候next数组的值要增加呢?
由前面的例子可知:
假设next[j]==k,可以推出P[0]~P[k-1]==P[j-k]~P[j-1],
如果想让next[j+1]==k,则需要满足P[0]~P[k]==P[j+1-k]~P[j],只需要在已知条件加上P[k]==P[j]
所以当P[j]==P[k]时,next[j+1]==k+1
如果P[j]!=P[k],我们就让new_k=next[k],再来判断P[j]是否等于P[new_k],如果相等P[j+1]==new_k+1
至此,我们就已经求出next数组中所有的值了
实现next数组
void GetNext(int* next, const char* P, size_t lenP)
{assert(next && P);if (lenP == 0)return;next[0] = -1;next[1] = 0;int j = 2;//下一项int k = 0;//前一项的kwhile (j < lenP)//next数组为遍历完{//k有可能回退到起始位置if (k == -1 || P[j - 1] == P[k]){next[j] = k + 1;j++;k++;}else{k = next[k];}}
}🚩理清思路
- 在发现主串与模式串匹配失败后,我们将j回退到某一个位置,这个位置由next[j]的值决定,因为next[j]存放的就是P[0]后面k个元素和P[j]前面k个元素完全相同的最大k值,回到下标为k的位置可以保证此时j的前面刚好有k个元素和i前面的k个元素相匹配,一步退到失配后最有可能匹配成功的地方(KMP算法只退到可能匹配成功的地方),不需要像BF算法在一次失配后接着试剩下的所有位置会不会成功
- 通过分析,我们得知了next数组得求值方法,当P[j]==P[k] (k==next[j]),next[j+1]==k+1
当P[j]!=P[k]时,另k==next[k]直到P[j]==P[k]
代码实现
void GetNext(int* next, const char* P, size_t lenP)
{assert(next && P);next[0] = -1;next[1] = 0;size_t j = 2;//下一项size_t k = 0;//前一项的kwhile (j < lenP)//next数组为遍历完{//k有可能回退到起始位置if (k == -1 || P[j - 1] == P[k]){next[j] = k + 1;j++;k++;}else{k = next[k];}}
}
int KMP(const char* S, const char* P)
{assert(S && P);int lenS = strlen(S);int lenP = strlen(P);int* next = (int*)malloc(sizeof(int) * lenP);assert(next);GetNext(next, P, lenP);int i = 0;int j = 0;while (i < lenS && j < lenP){if ((j == -1) || (S[i] == P[j])){i++;j++;}else{j = next[j];}}free(next);if (j >= lenP)return i - j;return -1;
}
优化next数组
将next数组优化为nextval数组
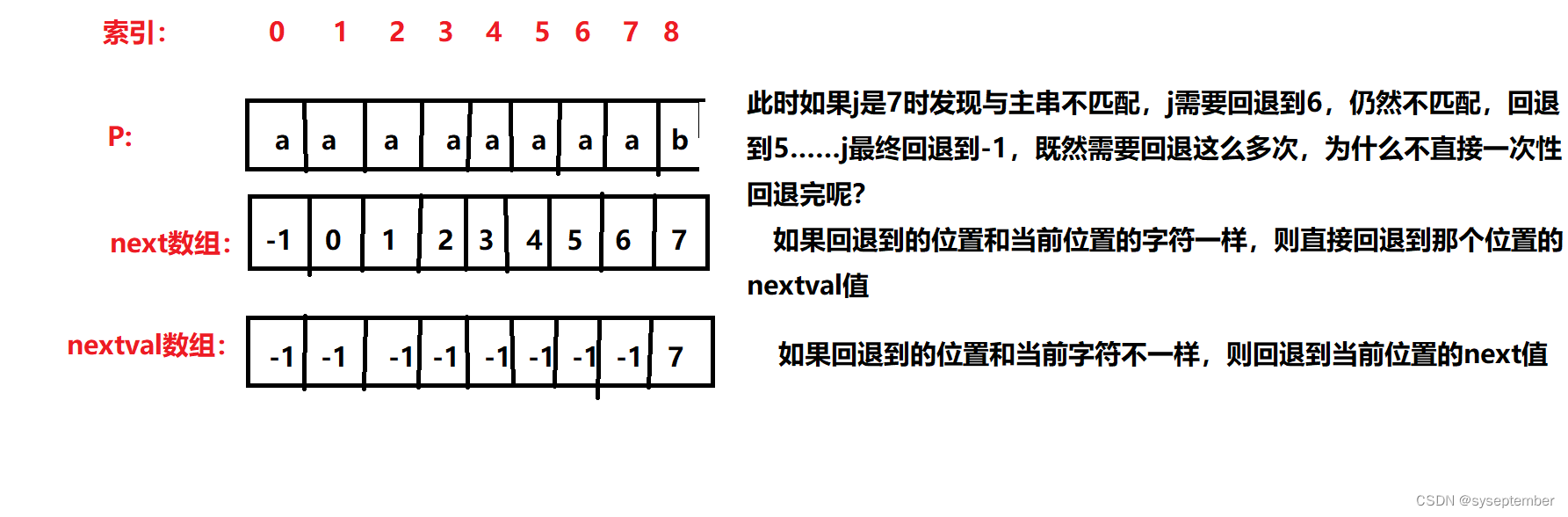
练习:
模式串 t=‘abcaabbcabcaabdab’ ,该模式串的 next 数组的值为( D ) , nextval 数组的值为 (F)
。
A. 0 1 1 1 2 2 1 1 1 2 3 4 5 6 7 1 2 B. 0 1 1 1 2 1 2 1 1 2 3 4 5 6 1 1 2
C. 0 1 1 1 0 0 1 3 1 0 1 1 0 0 7 0 1 D. 0 1 1 1 2 2 3 1 1 2 3 4 5 6 7 1 2
E. 0 1 1 0 0 1 1 1 0 1 1 0 0 1 7 0 1 F. 0 1 1 0 2 1 3 1 0 1 1 0 2 1 7 0 1
最终代码
void GetNext(int* next, const char* P, size_t lenP)
{assert(next && P);next[0] = -1;next[1] = 0;size_t j = 2;//下一项size_t k = 0;//前一项的kwhile (j < lenP)//next数组为遍历完{//k有可能回退到起始位置if (k == -1 || P[j - 1] == P[k]){next[j] = k + 1;j++;k++;}else{k = next[k];}}
}
//优化next数组
void GetNextVal(int* nextVal, const int* next, const char* P)
{assert(nextVal && next);nextVal[0] = -1;for (size_t i = 1; i < strlen(P); i++){//回退位置的字符等于当前字符,回退到那个位置的nextVal值处if (P[i] == P[next[i]]){nextVal[i] = nextVal[next[i]];}//回退的位置的字符不等于当前字符,回退到当前位置的next值处else{nextVal[i] = next[i];}}
}
int KMP(const char* S, const char* P)
{assert(S && P);int lenS = strlen(S);int lenP = strlen(P);int* next = (int*)malloc(sizeof(int) * lenP);int* nextVal = (int*)malloc(sizeof(int) * lenP);assert(next);GetNext(next, P, lenP);GetNextVal(nextVal, next, P);int i = 0;int j = 0;while (i < lenS && j < lenP){if ((j == -1) || (S[i] == P[j])){i++;j++;}else{j = nextVal[j];}}free(next);if (j >= lenP)return i - j;return -1;
}int main()
{char* str = "ababcabcdabcde";char* sub = "abcd";printf("%d\n", KMP(str, sub));return 0;
}
至此整个KMP算法我们已经实现了,不得不承认确实很复杂,我花了2个下午才弄明白😭,如果还有哪里不懂得地方,可以看看这个视频【完整版】终于有人讲清楚了KMP算法,Java语言C语言实现,一定要静下心来看!!!
相关文章:

字符串匹配【BF、KMP算法】
文章目录:star:BF算法代码实现BF的改进思路:star:KMP算法🚩next数组🚩代码实现优化next数组最终代码⭐️BF算法 BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将主串S的第一个字符与模式串P…...
Leetcode.1616 分割两个字符串得到回文串
题目链接 Leetcode.1616 分割两个字符串得到回文串 Rating : 1868 题目描述 给你两个字符串 a和 b,它们长度相同。请你选择一个下标,将两个字符串都在 相同的下标 分割开。由 a可以得到两个字符串: aprefix和 asuffix,…...

剑指 Offer II 033. 变位词组
题目链接 剑指 Offer II 033. 变位词组 mid 题目描述 给定一个字符串数组 strs,将 变位词 组合在一起。 可以按任意顺序返回结果列表。 注意:若两个字符串中每个字符出现的次数都相同,则称它们互为变位词。 示例 1: 输入: strs [“eat”,…...
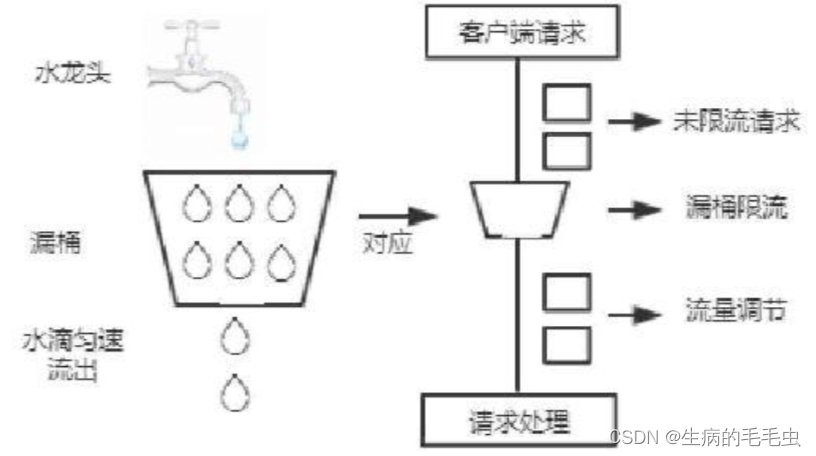
spring-cloud-sentinel ---流控算法---review
计数器算法 计数器算法,限定每个固定时间能处理的请求总数,例如1分钟100,如果在第一个一分钟,总共请求60次,接着第二个一分钟,counter又会从0 开始技术,如果在1.5分钟的时候,达到了…...
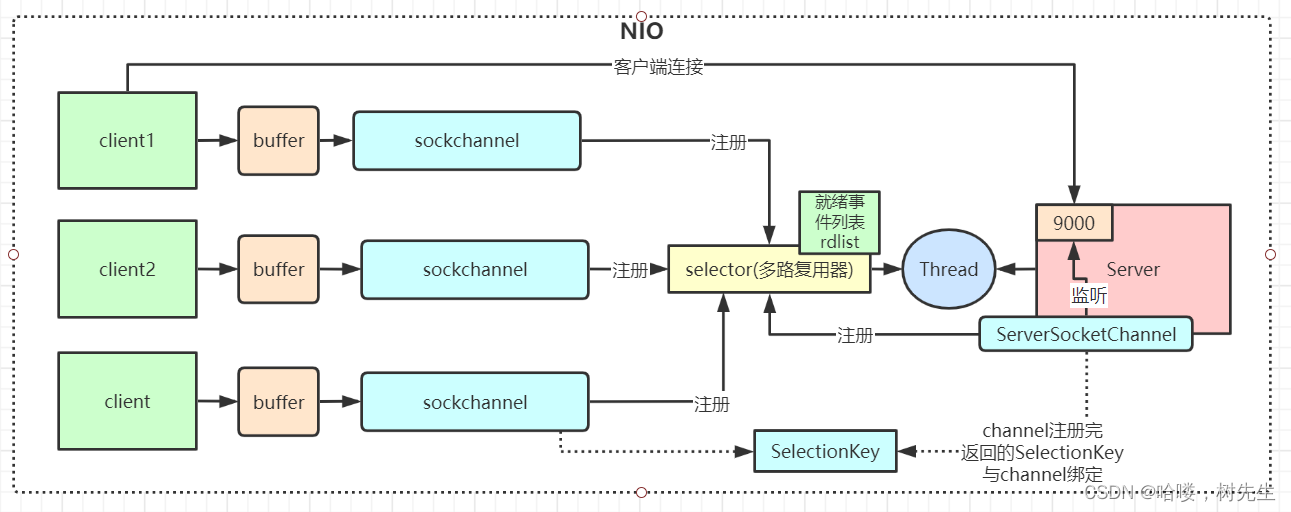
1.浅析NIO 多路复用器selector
一:IO基本介绍 Java共支持3种网络编程IO模式:BIO,NIO,AIO 0.Java对BIO、NIO、AIO的支持: Java BIO : 同步并阻塞,服务器实现模式为一个连接一个线程,即客户端有连接请求时服务器端…...
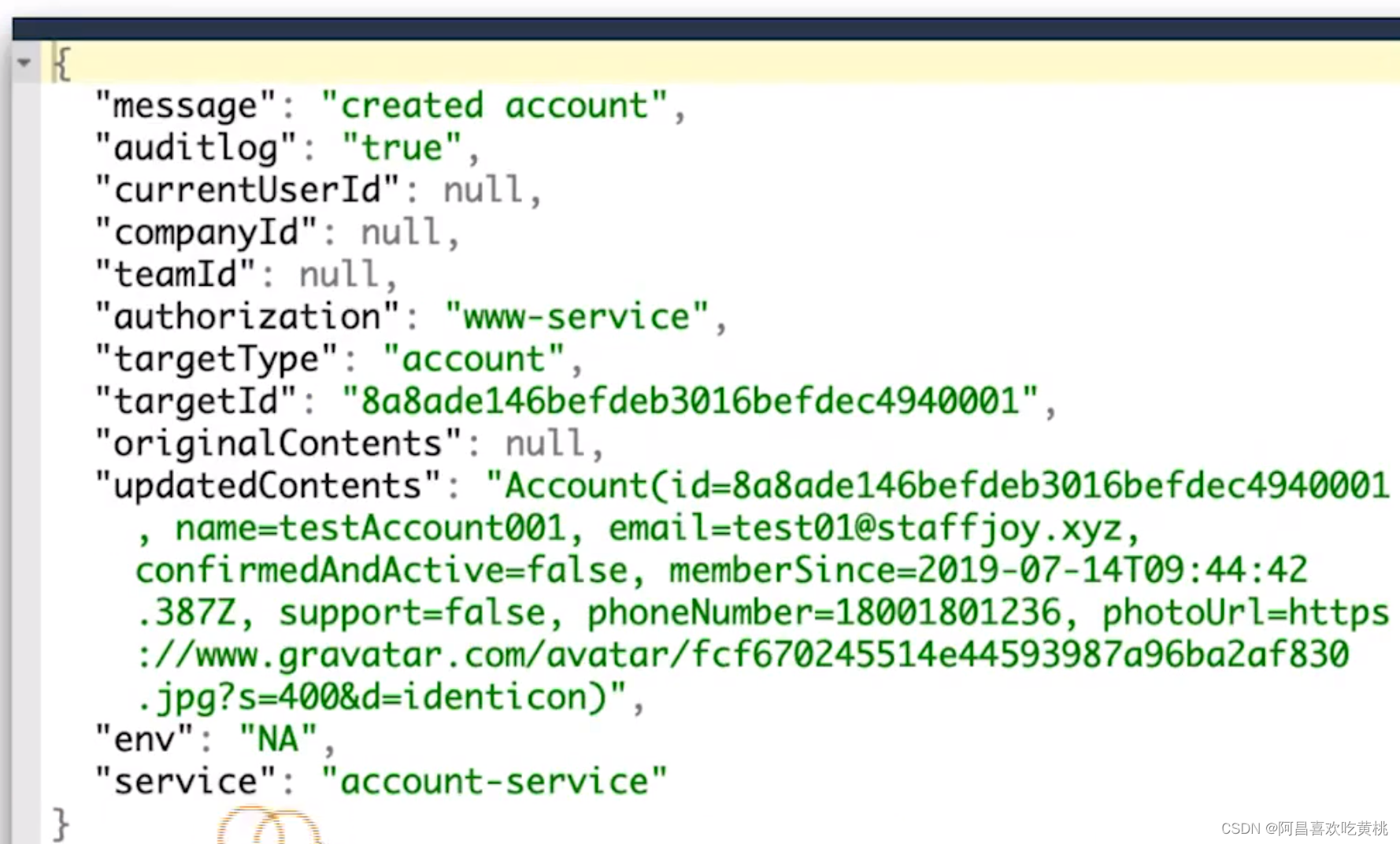
Day920.结构化日志业务审计日志 -SpringBoot与K8s云原生微服务实践
结构化日志&业务审计日志 Hi,我是阿昌,今天学习记录的是关于结构化日志&业务审计日志的内容。 1、什么是结构化日志 结构化日志(Structured Logging)是一种将日志信息组织为结构化数据的技术。 传统的日志通常是一些文…...
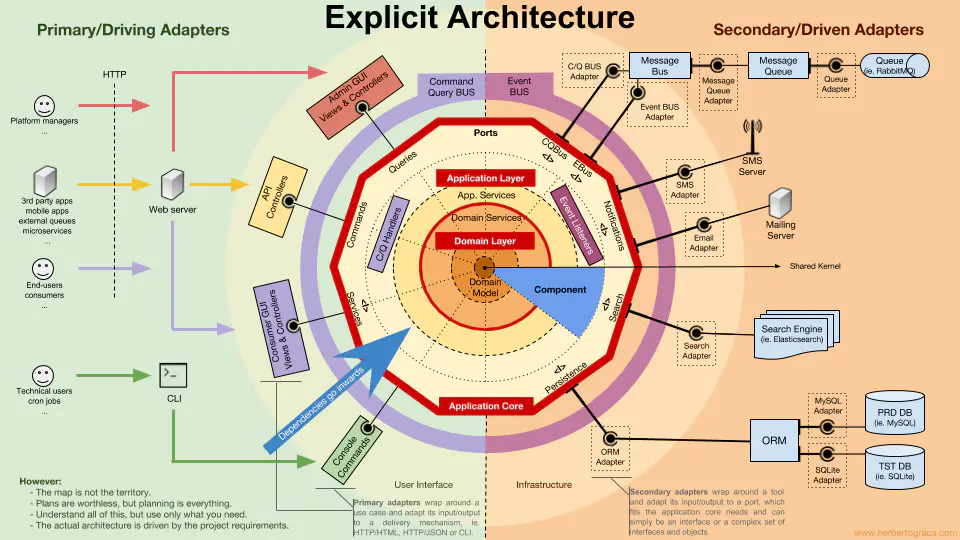
前端代码复用学习笔记:整洁架构与清晰架构
基础代码的复用往往比较简单,但是业务代码的复用通常是困难的,如果没有特殊的手段去治理项目会逐渐发展为难以维护的巨石应用,按照维基百科记载,代码的复用形式主要有三种,程序库,应用框架,设计…...

【python刷题】leecode官方提示“->“,“:“这些符号是什么意思?什么是Type Hints?
作者:20岁爱吃必胜客(坤制作人),近十年开发经验, 跨域学习者,目前于海外某世界知名高校就读计算机相关专业。荣誉:阿里云博客专家认证、腾讯开发者社区优质创作者,在CTF省赛校赛多次取得好成绩。…...

【华为OD机试真题2023 JAVA】最佳对手
华为OD机试真题,2023年度机试题库全覆盖,刷题指南点这里 最佳对手 知识点排序DFS搜索回溯 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 游戏里面,队伍通过匹配实力相近的对手进行对战。 但是如果匹配的队伍实例相差太大,对于双方游戏体验都不会太好。 给定n个…...
css实现文字大小自适应
在页面编写中经常会碰到页面自适应的问题,也就是页面内部的元素会随着窗口的放大缩小而放大缩小,box可以通过calc 百分比的形式做到页面自适应,但是box内的字体却无法做到这点,往往box自适应大小了,内部的字体还是原来…...
【Redis】搭建哨兵集群
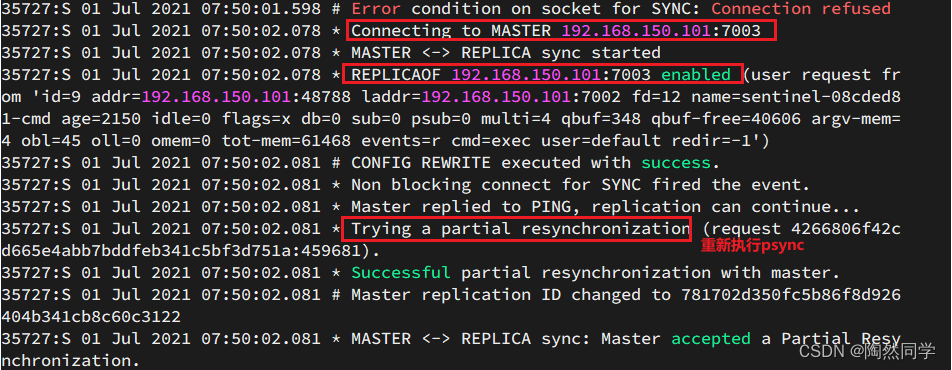
目录 集群结构 准备实例和配置 启动 测试 集群结构 这里我们搭建一个三节点形成的Sentinel集群,来监管之前的Redis主从集群。如图: 三个sentinel实例信息如下: 节点IPPORTs1192.168.150.10127001s2192.168.150.10127002s3192.168.150.…...
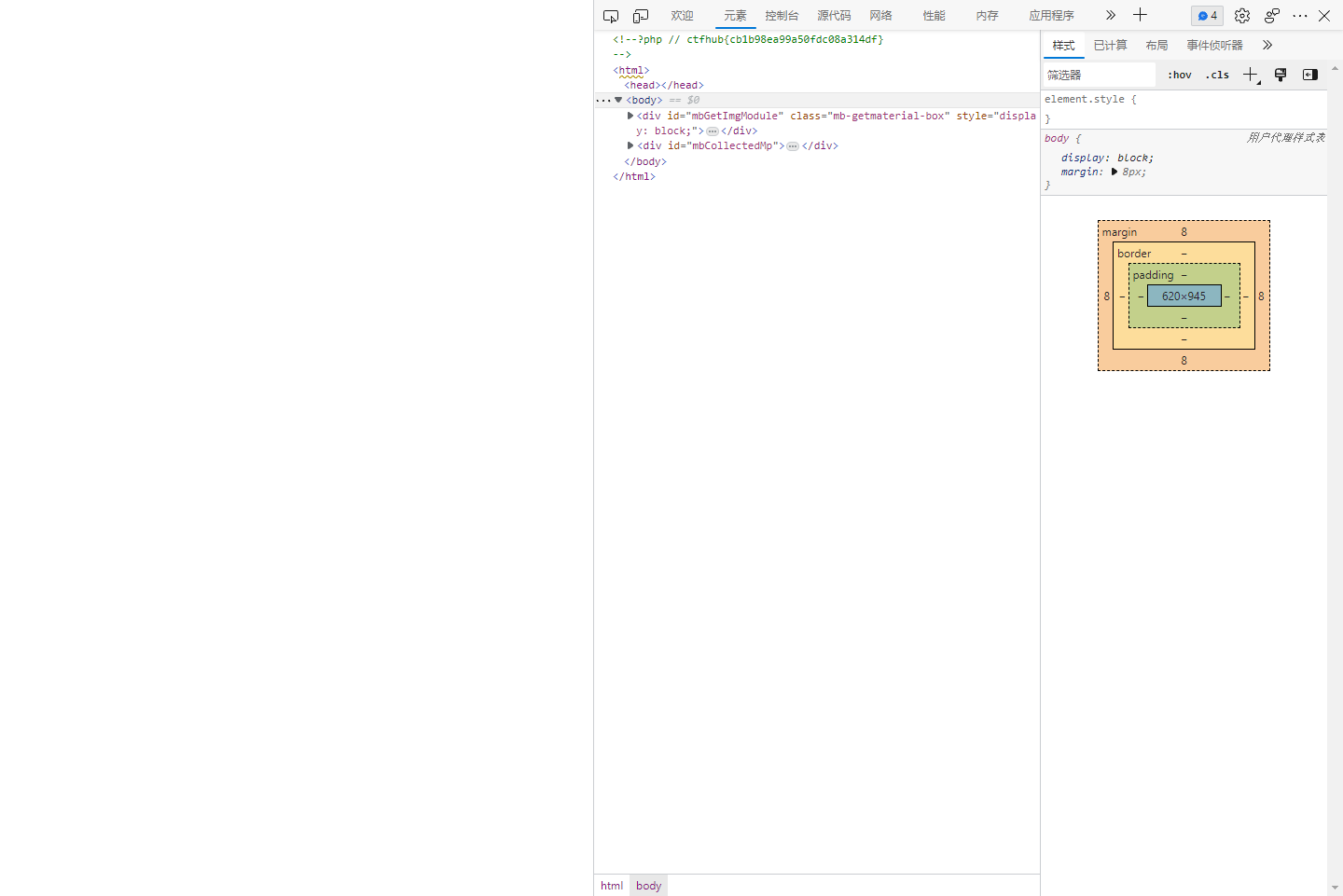
CTFHub | .htaccess
0x00 前言 CTFHub 专注网络安全、信息安全、白帽子技术的在线学习,实训平台。提供优质的赛事及学习服务,拥有完善的题目环境及配套 writeup ,降低 CTF 学习入门门槛,快速帮助选手成长,跟随主流比赛潮流。 0x01 题目描述…...

微机原理 || 8253 芯片 (详细讲解 + 经典例题)
一点点看!一定可以看懂!考试没有问题的!加油💪 前面知识写的详细,看不懂可以先看典例,回头来梳理就明白了【典例就是常考的题】 目录 Part 1: 芯片知识总结 (一)8253 芯片特点 …...
python Django高级操作-分页-定义CVS-发送邮件
分页 分页是指在web页面有大量数据需要显示,为了阅读方便在每个页页中只显示部分数据。优点: 1.方便阅读2.减少数据提取量,减轻服务器压力。Paginator对像 负责分页数据整体的管理对象的构造方法Paginator属性 Paginator方法 Paginator异常exception pag…...

React 用一个简单案例体验一遍 React-dom React-router React-redux 全家桶
一、准备工作 本文略长,建议耐心读完,每一节的内容与上一节的内容存在关联,最好跟着案例过一遍,加深记忆。 1.1 创建项目 第一步,执行下面的命令来创建一个 React 项目。 npx create-react-app react-example cd rea…...

9. C#面向对象基础
一、C# 类 在 C# 中,类是引用类型的。类由成员属性和成员方法构成。我们可以动态创建类的实例(instance),这个实例也被称为对象(object),我们可以通过类和对象来设计程序。 1、类的定义 类的定…...

【MIT 6.S081】Lab2: system calls
本Lab包括两个简单系统调用的实现,进一步熟悉系统调用接口。 笔者用时约1.5h 概述 根据文档说明,当我们添加一个系统调用时,比如第一个任务是添加一个trace,需要进行以下操作: 首先将系统调用的原型添加到user/user…...
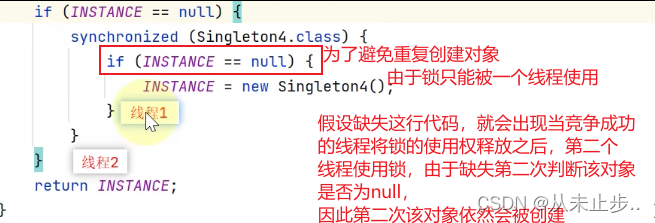
设计模式之单例模式~
设计模式包含很多,但与面试相关的设计模式是单例模式,单例模式的写法有好几种,我们主要学习这三种—饿汉式单例,懒汉式单例、登记式单例,这篇文章我们主要学习饿汉式单例 单例模式: 满足要点: 私有构造 …...

top终端详解
1.top命令行使用 2.top每行意义 3.补充 1.top命令行使用 top命令是一个常用的Linux系统命令,用于实时查看系统的运行状态和进程信息。下面是top命令的几个常用参数的含义: -d seconds:设置top命令的更新间隔时间,单位是秒。默认是…...

解决一个偶现的503 bug,花了俺不少时间
概述 在3月2日晚上,大概8点左右,本想打道回府,回家休息,突然被人在bug群了一下,说是管理后台,访问不了,界面上出现了: 503 service temporarily unavailable我赶紧尝试访问了一下,确…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...