数学建模--整数规划和非线性规划
目录
整数规划
非线性规划
总结
整数规划中分支定界法的具体步骤和实现细节是什么?
初始化:
分支:
定界:
剪枝:
终止条件:
非线性规划中的梯度法、牛顿法和拟牛顿法的比较分析有哪些?
梯度法
牛顿法
拟牛顿法
对比分析
收敛速度:
计算复杂度:
适用范围:
实现难度:
延伸
在实际应用中,整数规划和非线性规划的选择标准是什么?
整数规划的应用场景:
非线性规划的应用场景:
选择标准:
如何有效地求解混合整数规划问题?
非线性规划在资源配置领域的应用案例有哪些?
在数学建模中,整数规划和非线性规划是两种重要的优化方法,它们在实际应用中具有广泛的应用。
整数规划
整数规划(Integer Programming, IP)是指在规划问题中,决策变量必须取整数值。根据变量的约束条件不同,整数规划可以分为以下几类:
- 纯整数规划:所有决策变量都必须取整数值。
- 混合整数规划:部分决策变量为整数,另一部分为实数。
- 0-1整数规划:所有决策变量只能取0或1的值。
整数规划的基本求解方法包括分支定界法、割平面法和隐枚举法等。其中,分支定界法是通过逐步增加约束条件来缩小可行解的范围,最终找到最优解。此外,松弛模型也是常用的求解策略之一,即先去除整数约束,使用线性规划的方法求解,然后逐步添加整数约束进行修正。
非线性规划
非线性规划(Nonlinear Programming, NLP)是指目标函数或约束条件中包含至少一个非线性函数的优化问题。与线性规划相比,非线性规划的求解更为复杂且没有统一的通用算法,常见的求解方法包括梯度法、牛顿法、拟牛顿法和变尺度法等。这些方法各有优缺点,适用于不同的问题类型。
非线性规划广泛应用于工程、经济、物理和社会科学等领域,例如资源配置、生产管理和投资组合管理等。由于非线性规划对初始值敏感,因此在求解过程中通常需要选择合适的初始点,并可能需要多次尝试以确保找到全局最优解。
总结
整数规划和非线性规划在数学建模中各有其独特的应用场景和求解方法。整数规划主要用于需要决策变量取整数值的问题,而非线性规划则用于处理目标函数或约束条件为非线性的情况。理解这两种规划方法的特点及其适用场景,对于解决复杂的优化问题至关重要。
整数规划中分支定界法的具体步骤和实现细节是什么?
分支定界法(Branch and Bound, B&B)是求解整数规划问题的一种常用算法。其基本思想是通过逐步分解原问题并利用定界和剪枝技术来找到最优解。以下是具体的步骤和实现细节:
初始化:
- 首先,求解整数规划的松弛问题(即放宽整数条件的线性规划问题)。如果松弛问题没有可行解,则停止计算,因为原整数规划也没有可行解。
分支:
- 选择一个非整数解的变量 𝑥𝑖xi,在松弛问题中加入约束条件:𝑥𝑖≤[𝑥𝑖]xi≤[xi] 和 𝑥𝑖≥[𝑥𝑖]+1xi≥[xi]+1,从而生成两个新的松弛问题,称为分枝。
- 分支过程通常采用“两分法”,即将原问题的可行域分解为越来越小的子域。
定界:
- 对每个未被剪枝的节点进行定界操作。具体步骤包括:
- 解该节点的松弛问题,得到最优值 𝑧z 和最优解 𝑥∗x∗。
- 更新该节点的上界和下界:若目标为最大化,则上界为当前最大值;若目标为最小化,则下界为当前最小值。
- 如果松弛问题的最优解是整数,则直接得到整数规划的最优解;否则继续下一步。
剪枝:
- 剪枝的作用是删除那些肯定不存在最优解的分支,以加速收敛和简化运算。
- 检查所有分枝的解及目标函数值,若某分枝的解是整数并且目标函数值大于(最大值)等于其它分枝的目标值,则将其它分枝剪去不再计算;若还存在非整数解并且目标值大于整数解的目标值,需要继续分枝,再检查,直到得到最优解。
终止条件:
- 当所有分支都被处理完毕且找到一个满足整数要求的最优解时,算法终止。
通过上述步骤,分支定界法能够有效地求解整数规划问题,并且通过剪枝和定界技术显著提高求解效率。
非线性规划中的梯度法、牛顿法和拟牛顿法的比较分析有哪些?
在非线性规划中,梯度法、牛顿法和拟牛顿法是三种常用的优化算法。它们各自有独特的特点和应用场景,下面将对这三种方法进行比较分析。
梯度法
梯度法是一种基于一阶导数的优化方法,其基本思想是在目标函数的当前点处沿着负梯度方向进行搜索,以寻找函数的最小值。梯度法的优点在于实现简单,计算量相对较小,适用于大规模问题。然而,梯度法的收敛速度较慢,通常需要大量的迭代次数才能达到较高的精度。
牛顿法
牛顿法是一种基于二阶导数的优化方法,其基本思想是在目标函数的当前点处使用泰勒展开式来近似目标函数,并通过求解二次方程来确定下一步的搜索方向和步长。牛顿法的优点在于收敛速度快,尤其是在目标函数是凸函数时,可以快速收敛到全局最优解。然而,牛顿法需要计算和存储Hessian矩阵及其逆矩阵,这在高维问题中可能导致计算复杂度和内存消耗过高。
拟牛顿法
拟牛顿法是牛顿法的一种改进版本,旨在降低牛顿法的计算成本。拟牛顿法通过近似Hessian矩阵或其逆矩阵来代替真实的Hessian矩阵,从而减少计算负担。常见的拟牛顿法变种包括BFGS、DFP等。拟牛顿法的优点在于既能保持较快的收敛速度,又能避免牛顿法的高计算成本。此外,拟牛顿法通常具有较好的全局收敛性能,适用于非凸问题。
对比分析
收敛速度:
- 牛顿法:二阶收敛,收敛速度最快。
- 梯度法:一阶收敛,收敛速度最慢。
- 拟牛顿法:介于两者之间,通常比梯度法快,但比牛顿法慢。
计算复杂度:
- 牛顿法:较高,需要计算和存储Hessian矩阵及其逆矩阵。
- 梯度法:较低,只需计算梯度。
- 拟牛顿法:介于两者之间,通过近似Hessian矩阵来减少计算负担。
适用范围:
- 牛顿法:适用于目标函数是凸函数的情况。
- 梯度法:适用于大规模问题,但收敛速度较慢。
- 拟牛顿法:适用于非凸问题,具有较好的全局收敛性能。
实现难度:
- 牛顿法:实现较为复杂,需要精确计算Hessian矩阵及其逆矩阵。
- 梯度法:实现相对简单,只需计算梯度。
- 拟牛顿法:实现难度介于两者之间,需要设计合适的近似策略。
梯度法、牛顿法和拟牛顿法各有优缺点,在实际应用中应根据具体问题的特点选择合适的优化算法。
延伸
在实际应用中,整数规划和非线性规划的选择标准是什么?
在实际应用中,选择整数规划还是非线性规划主要取决于问题的特性。我们可以总结出以下几点:
整数规划的应用场景:
- 整数规划广泛应用于生产计划、生产调度、货车路径规划等领域。
- 它适用于需要考虑许多约束条件(如产能约束、人力资源约束等)的情况。
- 整数规划特别适合解决最优解为较小整数的问题。
非线性规划的应用场景:
- 非线性规划在生产与运输优化、金融风险控制等领域有广泛应用。
- 它主要用于解决具有非线性目标函数和约束条件的问题。
- 非线性规划在经济学、工程、生物学、物理学等多个领域得到了应用。
选择标准:
- 如果问题的最优解必须是整数,并且涉及多个约束条件,那么整数规划是一个更好的选择。
- 如果问题的目标函数或约束条件是非线性的,或者需要全局最优化,那么非线性规划更为合适。
在实际应用中,选择整数规划还是非线性规划应根据问题的具体需求和特性来决定。如果问题的最优解需要为整数并且涉及多个约束条件,则整数规划是更优的选择;
如何有效地求解混合整数规划问题?
有效地求解混合整数规划(MIP)问题可以采用多种方法,包括精确算法和启发式算法。以下是一些常见的方法:
分支定界法:这是最常用的精确算法之一。通过将问题分解为子问题,并逐步求解这些子问题来找到最优解。
割平面法:这种方法通过引入割平面来逐步排除不可行的解,从而缩小搜索空间,提高求解效率。
蒙特卡罗法:这是一种基于随机抽样的方法,适用于大规模问题的近似求解。
列生成法:这种方法通过生成新的变量来逐步构建最优解,特别适用于具有大量变量的问题。
拉格朗日松弛法:通过松弛约束条件,将原问题转化为一个更易求解的松弛问题,然后逐步恢复严格的约束条件。
神经网络与机器学习方法:DeepMind和谷歌的研究表明,使用神经网络和机器学习方法可以有效解决MIP问题。
群智能演化策略:基于金字塔结构的群智能演化策略(PES算法)能够平衡全局与局部搜索的能力,提升求解效率。
此外,还有一些专门的求解器和工具可以帮助求解MIP问题:
- GAMS:提供多种求解器,如sbb用于混合整数非线性规划模型,gams/snopt用于连续二次规划等。
- SCIP:一个强大的数学规划求解器,支持线性、混合整数和混合整数二次约束的规划模型。
- OR-Tools:提供灵活且高效的求解方法,适用于具有混合整数和非线性特性的优化问题。
非线性规划在资源配置领域的应用案例有哪些?
非线性规划在资源配置领域有广泛的应用,以下是一些具体案例:
在机械加工车间中,通过分析制造资源状态信息,建立了一个以最短加工时间、最低加工成本和最优制造资源状态为目标的非线性工艺规划资源优化配置模型。该模型旨在提高设计工艺的车间生产可执行性。
结合SWAT径流模拟模型与多目标非线性规划模型,提出了一个天气驱动的多水源动态优化分配模型。该模型考虑了供水量的波动,并微调了灌区不同水源、不同渠道和不同作物生育期的水资源分配,以实现水供需平衡、经济效益最大化和水分配公平。
为提高沙漠治理效益并提升水资源利用效率,构建了一个以固碳制氧总价值最大和用水效率最大为目标的治沙区非线性分式多目标水土资源优化配置模型。该模型对治沙区植物种植结构和植物生长季灌水量进行联合优化配置。
针对多个合作码头泊位分配、岸机分配、堆场分配等问题,提出了一个混合整数非线性规划模型,旨在最小化所有码头的总运营成本。通过嵌入列生成和CPLEX的定制自适应大邻域搜索(ALNS)算法来解决实际大小的实例。
无线通信网络资源的分配优化通常描述为混合整数非线性规划问题。为了降低计算复杂度并确保最优性能,提出利用二进制鲸鱼优化算法进行无线资源分配。
相关文章:

数学建模--整数规划和非线性规划
目录 整数规划 非线性规划 总结 整数规划中分支定界法的具体步骤和实现细节是什么? 初始化: 分支: 定界: 剪枝: 终止条件: 非线性规划中的梯度法、牛顿法和拟牛顿法的比较分析有哪些?…...

Linux-查看dd命令进度
查看dd命令进度 一、概述1. 在一个终端执行拷贝任务2. 在另一终端执行进度命令 一、概述 系统:Ubuntu 22.04 在使用 dd 命令做拷贝大量数据的时候,因为并没有输出,所以比较难判断当前进度,因此可以使用下面的命令作为进度查看 …...

高效微调 100 多种大语言模型:先计算法,急速推理!
hiyouga/LLaMA-Factoryhttps://github.com/hiyouga/LLaMA-Factory Stars: 26.9k License: Apache-2.0 LLaMA-Factory 是一个用于高效微调 100 多个大型语言模型(ACL 2024)的 WebUI。 多种模型:LLaMA、LLaVA、Mistral、Mixtral-MoE、Qwen、Y…...

opencv grabCut前景后景分割去除背景
参考: https://zhuanlan.zhihu.com/p/523954762 https://docs.opencv.org/3.4/d8/d83/tutorial_py_grabcut.html 环境本次: python 3.10 提取前景: 1、需要先把前景物体框出来 需要坐标信息,可以用windows自带的画图简单提取像素…...

qt--电子相册
一、项目要求 设计一个电子相册,点击上一张,切换到上一张图片,点击下一张,切换到下一张图片。 要求:图片的展示可以循环(QList<QString>) 要求:界面美观 二、项目代码 本质是通…...

【MSP430】MSP430F5529几个定时器
MSP430F5529共有四个定时器,其中三个是Timer_A定时器,一个是Timer_B定时器。 这些定时器在MSP430F5529微控制器中发挥着重要的作用,不仅支持多重捕获/比较、PWM输出和内部定时功能,还具有丰富的中断处理能力。这些特性使得MSP430…...
苍穹外卖(一)之环境搭建篇
Ngnix启动一闪而退 启动之前需要确保ngnix.exe的目录中没有中文字体,在conf目录下的nginx.conf文件查看ngnix的端口号,一般默认为80,若80端口被占用就会出现闪退现象。我们可以通过logs/error.log查看错误信息,错误信息如下&…...
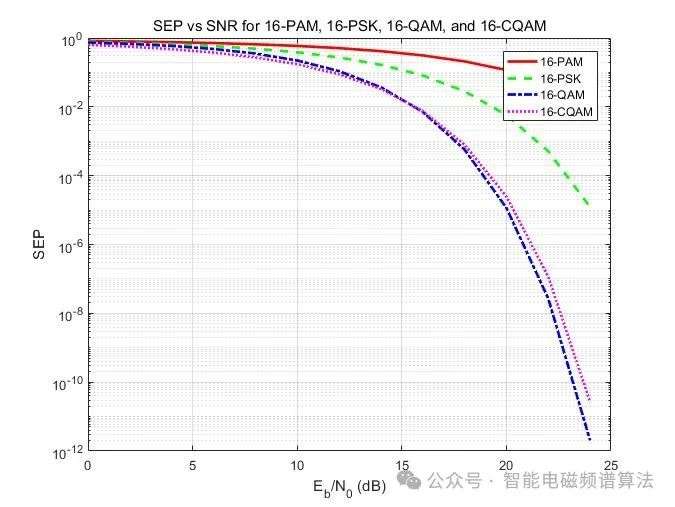
【限免】16PAM、16PSK、16QAM、16CQAM星座图及误码率【附MATLAB代码】
微信公众号:智能电磁频谱算法 QQ交流群:949444104 主要内容 MATLAB代码 % Parameters M 16; N 4; % Number of circles for CQAM SNR_dB 0:2:25; % Extended SNR range to reach higher values num_symbols 1e5; % Total number of symbols for s…...

09-软件易用性
易用性是用户体验的一个重要方面,网站建设者一般会沉溺于自己的思维习惯,而造成用户使用的不畅。易用性不仅是专业UI/UE人员需要研究,对于网站建设其他岗位的人也应该了解一定的方法去检验和提升网站的易用性。通常对易用性有如下定义: 易理解…...

FPGA开发——独立仿真和联合仿真
一、概述 我们在进行FPGA开发的过程之中,大部分情况下都是在进行仿真,从而验证代码实现结果的正确与否,这里我们引入了独立仿真和联合仿真进行一个简单介绍。 联合仿真:一般我们在进行仿真之前需要在相应的软件中建立相应的工程…...

基于STM32瑞士军刀--【FreeRTOS开发】学习笔记(二)|| 堆 / 栈
堆和栈 1. 堆 堆就是空闲的一块内存,可以通过malloc申请一小块内存,用完之后使用再free释放回去。管理堆需要用到链表操作。 比如需要分配100字节,实际所占108字节,因为为了方便后期的free,这一小块需要有个头部记录…...

ABAP+从SAP发出去的PDF文件在第三方系统出现乱码
这是一个 ABAP转换PDF调用函数CALL FUNCTION CONVERT_OTF的问题记录,关乎字体STSong-Light-ldentity-H 和 STSong-Light的区别 背景: 做了一个增强,是采购订单审批后自动发送采购订单PDF1到企业微信,用户再将企业微信收到的P…...
)
基于springsecurity的会话并发处理功能(附代码)
1. 需求 在项目中往往需要实现一个限制不同设备同时登录的功能,比如我只允许同一时间只有一个客户端能登录,而其他的已登陆的客户端会被挤出来 而springsecurity中恰好就帮我们实现好了对应的接口功能,我们只需要自定义配置就好 2. 结合sp…...
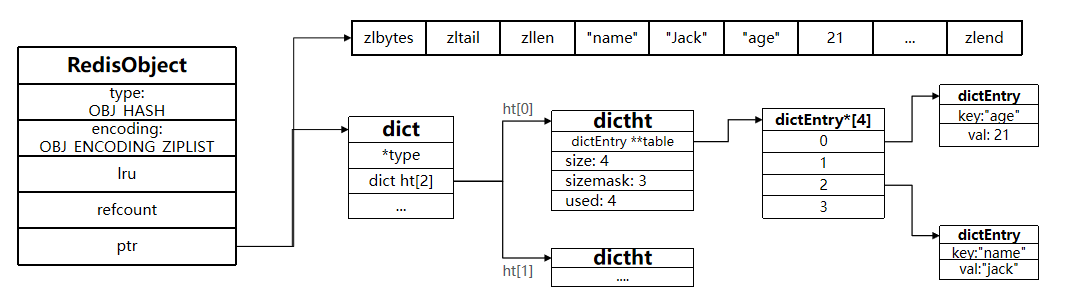
Redis底层数据结构的实现
文章目录 1、Redis数据结构1.1 动态字符串1.2 intset1.3 Dict1.4 ZipList1.5 ZipList的连锁更新问题1.6 QuickList1.7 SkipList1.8 RedisObject 2、五种数据类型2.1 String2.2 List2.3 Set2.4 ZSET2.5 Hash 1、Redis数据结构 1.1 动态字符串 Redis中保存的Key是字符串…...

制作excel模板,用于管理后台批量导入船舶数据
文章目录 引言I 数据有效性:基于WPS在Excel中设置下拉框选择序列内容II 数据处理:基于easyexcel工具实现导入数据的持久化2.1 自定义枚举转换器2.2 ExcelDataConvertExceptionIII 序列格式化: 基于Sublime Text 文本编辑器进行批量字符操作引言 需求: excel数据导入模板制…...

领略诗词之妙,发觉生活之美。
文章目录 引言落霞与孤鹜齐飞,秋水共长天一色。野渡无人舟自横。吹灭读书灯,一身都是月。我醉欲眠卿且去,明朝有意抱琴来。赌书消得泼茶香,当时只道是寻常。月上柳梢头,人约黄昏后。最是人间留不住,朱颜辞镜花辞树。山中何事?松花酿酒,春水煎茶。似此星辰非昨夜,为谁风…...
基于FFmpeg和SDL的音视频解码播放的实现过程与相关细节
目录 1、视频播放器原理 2、FFMPEG解码 2.1 FFMPEG库 2.2、数据类型 2.3、解码 2.3.1、接口函数 2.3.2、解码流程 3、SDL播放 3.1、接口函数 3.2、视频播放 3.3、音频播放 4、音视频的同步 4.1、获取音频的播放时间戳 4.2、获取当前视频帧时间戳 4.3、获取视…...

SSIS_SQLITE
1.安装 SQLite ODBC 驱动程序 2.添加SQLite数据源 在“用户DSN”或“系统DSN”选项卡中,点击“添加”。选择“SQLite3 ODBC Driver”,然后点击“完成”。在弹出的配置窗口中,设置数据源名称(DSN),并指定S…...

Redis 7.x 系列【27】集群原理之通信机制
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 概述2 节点和节点2.1 集群拓扑2.2 集群总线协议2.3 流言协议2.4 心跳机制2.5 节点握…...
【五】MySql8基于m2芯片arm架构Ubuntu24虚拟机安装
文章目录 1. 更新系统包列表2. 安装 MySQL APT Repository3. 更新系统包列表4. 安装 MySQL Server5. 运行安全安装脚本6. 验证 MySQL 安装7. 配置远程连接7.1 首先要确认 MySQL 配置允许远程连接:7.2 重启 MySQL 服务:7.3 检查 MySQL 用户权限࿱…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
