初识C++ · AVL树(2)
目录
前言:
1 左右旋
2 右左旋
3 部分细节补充
3.1 单旋和插入
3.2 部分小函数
前言:
AVL树作为一种结构,理解树的本身是不大难的,难的在于,树旋转之后的连接问题,写AVL树的代码大部分都是在旋转部分,所以连接问题是比较需要细心的,那么这里来说呢,把细心做好,变量的位置放好,连接的次序连接对,就成功了。
1 左右旋
前文提及,什么情况下需要左右旋?即不是纯粹的左边高或者是右边高,那么使用到左右旋的情况如下:

如果我们固执的以为在b 或者 c插入数据之后,90的平衡因子变为了-2,右旋就能解决问题的话就完蛋啦,这里我们直接对90右旋之后,结果就是镜像的,树还是没有平衡,那么我们再左旋,相当于旋转回来了,整个树的结果是没有变的。
此时就需要左旋转后再右旋转,可能有人会问,这个图是什么意思,我们使用的是抽象图来介绍,这样更加方便,长方形代表的就是高度为多少的子树。
选择b c作为例子,当我们往b c插入数据的时候,90的平衡因子变为了-2,此时parent就是90,那么我们需要一个操作让该树变成完全的左子树高,这样再右旋转,才可以保持平衡,那么如何变成完全的左子树高呢?
记住那两个线,30 -90 30 -60的这两条线,只要60在30和90的中间就是完全的左子树高,所以我们需要对30进行左旋,所以现在已知的操作就是先左旋再右旋,要记得参数不是一样的。
旋转的问题很好解决,旋转中的问题可不止旋转,这里还有平衡因子的问题,我们不难发现,在b 或者 c插入数据之后平衡因子的改变不是一样的,甚至来说如果h = 1,即60是新插入的,平衡因子的改变也是不一样的。
所以平衡因子的变化可以分为三个情况,一是b插入,二是c插入,三是60是新插入的,其中平衡因子的变化就留给读者自己发现啦,这是比较简单的,所以代码就可以出来了:
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//先左旋 再右旋RotateL(subL);RotateR(parent);//更新平衡因子if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if(bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}//60自己就是新插入的节点else if(bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}我们知道,以某个节点作为平衡节点,平衡之后该节点的父节点平衡因子必定为0,所以我们可以把subLR = 0直接提取出来。所以双旋来说是很简单,甚至比单旋都简单。
2 右左旋
有了左右旋的基础,这里直接就给代码了:
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//旋转完成RotateR(subR);RotateL(parent);//更新平衡因子subRL->_bf = 0;//RL必平衡if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;}else{assert(false);}}3 部分细节补充
是不是以为AVL树到这里就要结束了?
错辣!还有许多细节要注意!
3.1 单旋和插入
单旋这里除了要注意旋转的时候的连接问题,还要注意变量的声明次序问题:
Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;Node* pparent = parent->_parent;parent->_parent = subL;以右旋为例子,当parent节点不是根节点,势必涉及到parent的父节点的连接问题,所以我们先声明了pparent,如果我们在这个if里面声明:
if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}在此之前pparent的值就已经变为了subL,所以pparent一定要在parent->_parent = subL之前声明了。
其次,插入这里:
//更新平衡因子
cur->_parent = parent;
while (parent)
{if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{//理论而言不可能出现这种情况assert(false);}
}为什么旋转之后就要break了呢?按道理来说,比如双旋之后,parent的位置必然改变,可能直接变成了叶子节点,如果再走循环,平衡因子必然改变,此时树的结构就被破坏了,所以一定要break了。
现在解释上文说的,为什么旋转之后,比如单旋,平衡因子一定变为0了?这里我们就借助抽象图来理解,具象图没有那么好理解:

以这个图作为例子,c插入数据之后,n成为了新的根节点,此时左子树的高度是 h(m) + h = h + 1,右子树的高度是h + 1,1是新插入的数据,所以平衡因子必定为0,该结论在左右双旋里面也有体现。
3.2 部分小函数
这里的函数就是用来测试的函数,没有什么值得特别注意的:
void InOrder(){_InOrder(_root);cout << endl;}bool IsBalance(){return _IsBalance(_root);}int Height(){return _Height(_root);}int Size(){return _Size(_root);}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;return max(_Height(root->_left), _Height(root->_right)) + 1;}bool _IsBalance(Node* root){if (root == nullptr)return true;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);// 不平衡if (abs(leftHeight - rightHeight) >= 2){cout << root->_kv.first << endl;return false;}// 顺便检查一下平衡因子是否正确if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalance(root->_left)&& _IsBalance(root->_right);}测试代码:
void TestAVLTree1()
{int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t1;for (auto e : arr){if (e == 13){int i = 0;}t1.Insert({ e,e });cout << "Insert:" << e << "->" << t1.IsBalance() << endl;}t1.InOrder();cout << t1.IsBalance() << endl;
}void TestAVLTree2()
{const int N = 100000000;vector<int> v;v.reserve(N);srand((unsigned)time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 确定在的值for (auto e : v){t.Find(e);}//随机值for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}下场剧透~因为AVL树的查找实在太快,但是对于平衡因子的控制要求太严格了,所以红黑树出现了,红黑树是一种近似平衡的结构~
感谢阅读!
相关文章:

初识C++ · AVL树(2)
目录 前言: 1 左右旋 2 右左旋 3 部分细节补充 3.1 单旋和插入 3.2 部分小函数 前言: AVL树作为一种结构,理解树的本身是不大难的,难的在于,树旋转之后的连接问题,写AVL树的代码大部分都是在旋转部分…...

LLM:归一化 总结
一、Batch Normalization 原理 Batch Normalization 是一种用于加速神经网络训练并提高稳定性的技术。它通过在每一层网络的激活值上进行归一化处理,使得每一层的输入分布更加稳定,从而加速训练过程,并且减轻了对参数初始化的依赖。 公式 …...

蓝桥杯 2024 年第十五届省赛真题 —— 最大异或结点
目录 1. 最大异或结点1. 问题描述2. 输入格式3. 输出格式4. 样例输入5. 样例输出6. 样例说明7. 评测用例规模与约定 2. 解题思路1. 解题思路2. AC_Code 1. 最大异或结点 1. 问题描述 小蓝有一棵树,树中包含 N N N 个结点,编号为 0 , 1 , 2 , ⋯ , N − 1 0,1,2,…...

AV1技术学习:Loop Restoration Filter
环路恢复滤波器(restoration filter)适用于64 64、128 128 或 256 256 像素块单元,称为 loop restoration units (LRUs)。每个单元可以独立选择是否跳过滤波、使用维纳滤波器(Wiener filter)或使用自导滤波器&#…...

如何使用python实现自动化办公?干货满满!
Python作为一种简单而强大的编程语言,不仅在数据科学和软件开发领域广受欢迎,还在办公自动化方面发挥了巨大作用。通过Python,我们可以编写脚本来自动执行各种重复性任务,从而提高工作效率并减少错误。在本文中,我们将…...
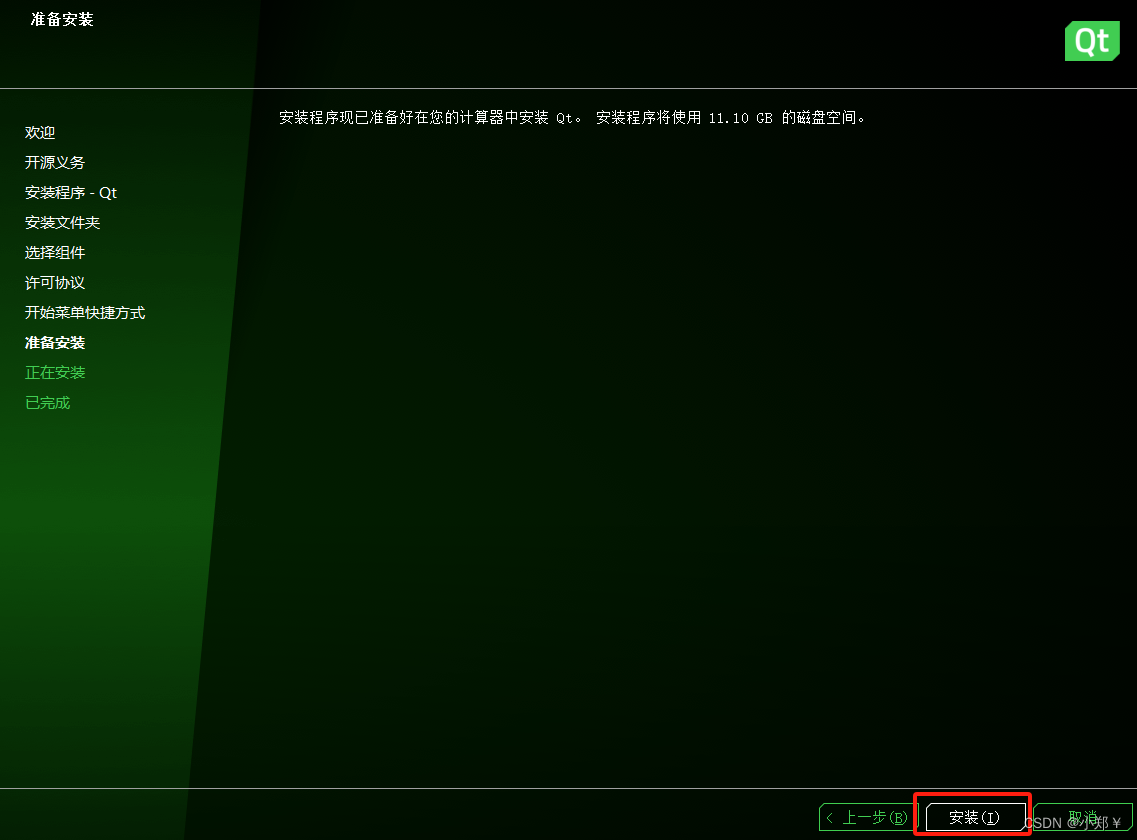
QT Creator下载安装详细教程(保姆级教程)
qt下载安装 1.下载网址 通过清华大学开源软件镜像站进行下载:链接: https://mirrors.tuna.tsinghua.edu.cn/qt/development_releases/online_installers/ 这里我选的是4.4版本的,也可以选择4.7版本,问题不大。 根据电脑系统选择下载linux…...

无人机公司销售需要什么资质
国家民航局于2024年1月1日实施了《无人驾驶航空器飞行管理暂行条例》,根据这个管理条例里面的 第十一条 使用除微型以外的民用无人驾驶航空器从事飞行活动的单位应当具备下列条件,并向国务院民用航空主管部门或者地区民用航空管理机构申请取得民用无人驾…...

代码自动化重构工具OpenRewrite介绍
OpenRewrite 是一个用于大规模自动化代码重构的开源框架,它极大地提升了开发人员的研发效率,通过自动化地进行代码重构和转换,帮助开发人员消除代码库中的技术债务。 通过 LST、访问器和配方的结合,OpenRewrite 能够实现准确的代…...
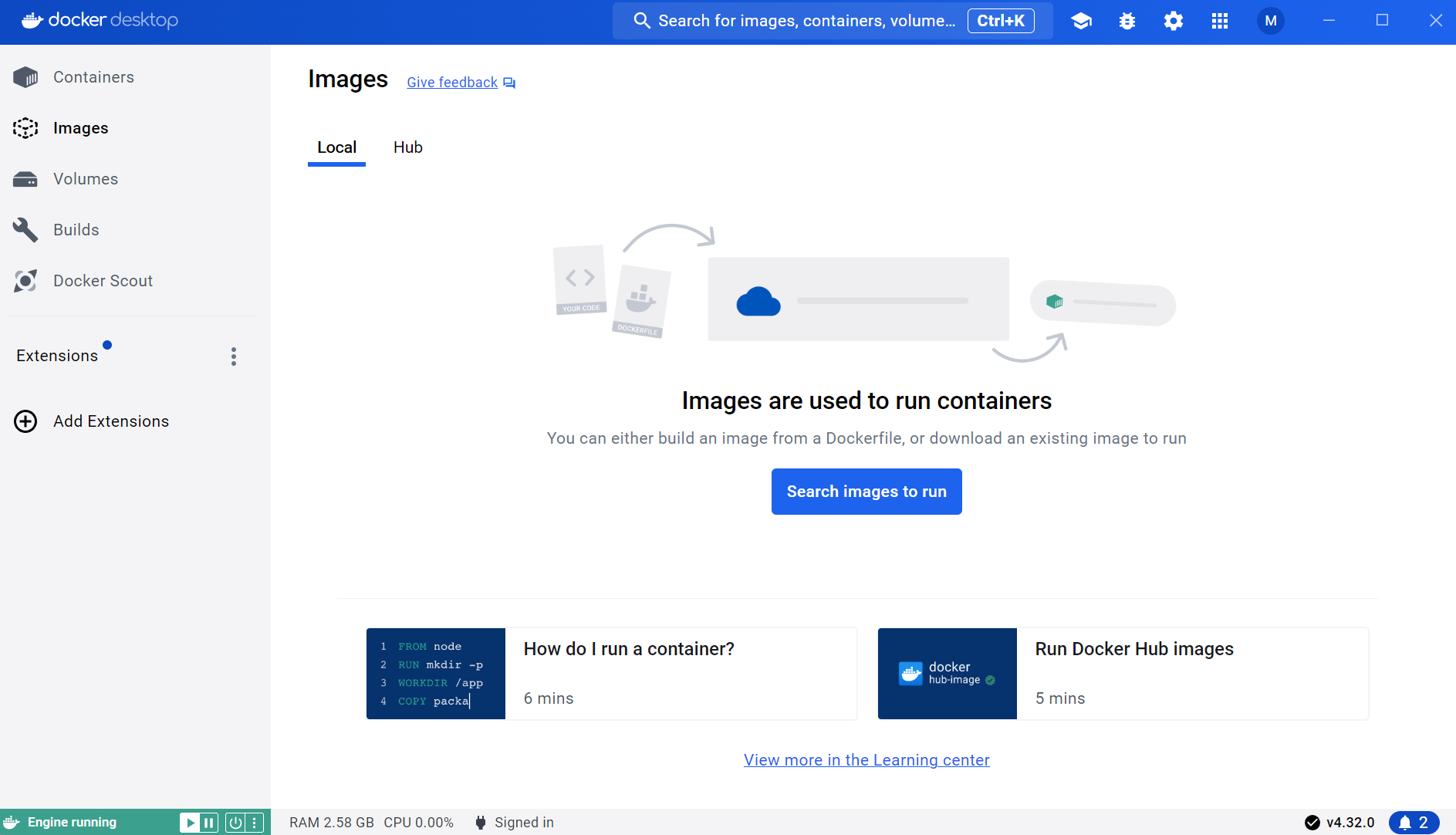
Win11安装Docker
下载Docker Desktop for Windows 下载 下载连接:Install Docker Desktop on Windows | Docker Docs 地址在国外,需要科学上网。也可使用我提供的,百度网盘:https://pan.baidu.com/s/1232TTkkzLsoZyFjC3bmgiQ 安装 下载完成之后…...

Windows电脑如何启动RTSP服务实现本地摄像头数据共享
技术背景 提起Windows共享本地摄像头,好多人想到的是通过ffmepg或vlc串流到服务器,实际上,用轻量级RTSP服务更简单,本文就介绍下,如何用大牛直播SDK的Windows轻量级RTSP服务,采集摄像头,生成本…...

探索 Spring WebFlux:构建响应式 Web 应用
探索 Spring WebFlux:构建响应式 Web 应用 随着互联网的发展,传统的同步编程模型已经难以应对高并发和高吞吐量的需求。为了解决这些问题,响应式编程逐渐成为主流。Spring WebFlux 是 Spring 5 引入的一个响应式 Web 框架,它基于…...

C# 植物大战僵尸
Winform 版本开发 高效率、流畅植物大战僵尸 git地址:冯腾飞/植物大战僵尸...

css 作业 2
文章目录 前言第四题第五题第六题第七题第八题第九题第十题(子标签) 前言 昨天写了前面三次作业,今天把剩下的七个作业写完 第四题 http://127.0.0.1:5500/index1.html,就用这个网址查看代码在网页的展示效果 代码评测过不了&…...

axios在vue中的使用
文章目录 一、axios是什么?二、使用步骤2.1 下载2.2 引入2.3 使用Get请求Post请求Forms 三、封装 一、axios是什么? Axios 是一个基于 promise 网络请求库,作用于node.js 和浏览器中。 它是 isomorphic 的(即同一套代码可以运行在浏览器和no…...

FastAPI(七十七)实战开发《在线课程学习系统》接口开发-- 课程编辑和查看评论
源码见:"fastapi_study_road-learning_system_online_courses: fastapi框架实战之--在线课程学习系统" 课程编辑 先来看下课程编辑 1.判断是否登录 2.判断课程是否存在 3.是否有权限(只有自己可以修改自己的课程) 4.名称是否重复…...

【JavaEE初阶】线程的概念及创建
目录 📕 前言 📕 认识线程(Thread) 🚩 概念 😊线程是什么 🙂 为啥要有线程 😭 进程和线程的区别(面试题重点) 🤭 Java的线程和操作系统线程…...

0727,学什么学,周六就应该休息!!!!!
周六就应该休息,一天就忙了两小时也不是我的错喵 目录 UDP的小总结 01:使用select实现一个基于UDP的一对一即时聊天程序。 1.0 复读机服务器和树洞客户端 2.0 byby不了一点的敬业服务器!!! 今天到此为止&#x…...

【C#】获取DICOM图像像素的像素值
8位像素深度的像素值 public byte GetGreyValue(int x, int y) {x Math.Min(x, m_nWidth - 1);y Math.Min(y, m_nHeight - 1);unsafe{byte* greyValue (byte*)m_pDicomData.ToPointer() y * m_nWidth x;return *greyValue;} } 16位像素深度的像素值 public ushort GetG…...
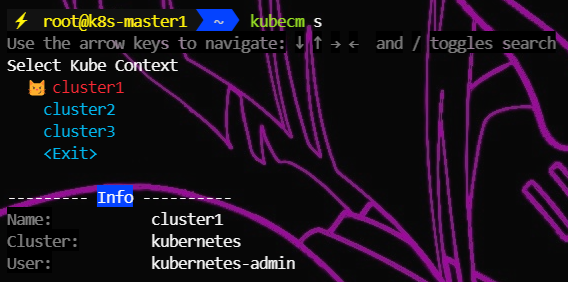
k8s多集群管理工具kubecm
文章目录 一、概述二、安装1、官网链接2、各平台安装2.1、MacOS2.2、Linux2.3、Windows 三、实例1、验证2、配置kubecm自动补全(选做)2.1、Bash2.2、Zsh2.3、fish2.4、PowerShell 3、创建存放kubeconfig文件的目录4、添加到 $HOME/.kube/config4.1、kube…...

通过 WSL 2 在Windows 上挂载 Linux 磁盘
原文查看 曾为了传输或者共享不同系统的文件频繁地在 Windows 和 Linux 系统之间切换,效率过低,所以尝试通过 WSL 2 在Windows 上挂载 Linux 磁盘。 先决条件 需要在Windows 10 2004 及更高版本(Build 19041 及更高版本)或 Win…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
