睿抗2024省赛----RC-u4 章鱼图的判断
题目
对于无向图 G=(V,E),我们将有且只有一个环的、大于 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。
给定一个无向图,请你判断是不是只有一个章鱼子图存在。
输入格式:
输入第一行是一个正整数 T (1≤T≤5),表示数据的组数。
每组数据的第一行是两个正整数 N,M (1≤N,M≤105),表示给定的无向图有 N 个点,M 条边。
接下来的 M 行,每行给出一条边两个端点的顶点编号。注意:顶点编号从 1 开始,并且题目保证任何边不会重复给出,且没有自环。
输出格式:
对于每组数据,如果给定的图里只有一个章鱼子图,则在一行中输出 Yes 和章鱼子图环的大小(及环中顶点数),其间以 1 个空格分隔。
否则,则在一行中输出 No 和图中章鱼子图的个数,其间以 1 个空格分隔。
输入样例:
3
10 10
1 3
3 5
5 7
7 9
1 2
2 4
2 6
3 8
9 10
1 9
10 10
1 3
3 5
5 7
7 9
9 1
1 2
2 4
4 8
8 10
10 1
10 10
1 3
3 5
5 7
7 9
9 1
2 4
4 8
8 10
10 2
10 6输出样例:
Yes 5
No 0
No 2做法
并查集判环。
#include<bits/stdc++.h>
using namespace std;
int n,m,t;
int fa[100010];
int huan[100010];//每个连通块环的数量
int ans;
int dis[100010];//环的长度
vector<int> g[100010];//存边
int st,ed;//环的头和尾
int getfa(int x){if(fa[x]==x) return x;return fa[x]=getfa(fa[x]);
}
void setfa(int x,int y){fa[getfa(x)]=getfa(y);
}
queue<int> q;
int main(){cin>>t;while(t--){ans=0;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) g[i].clear(),fa[i]=i,huan[i]=0,dis[i]=0;for(int i=1;i<=m;i++){int a,b;scanf("%d%d",&a,&b);g[a].push_back(b);g[b].push_back(a);if(getfa(a)==getfa(b)) {//环出现 huan[getfa(a)]++;st=a,ed=b;}else{huan[getfa(b)]+=huan[getfa(a)];//不可以先setfa,不然根就不是原来的根了 setfa(a,b);}}for(int i=1;i<=n;i++){if(getfa(i)==i&&huan[i]==1){//看有多少个 连通块 是环为1的 ans++;}}if(ans!=1) {cout<<"No "<<ans<<endl;continue;}dis[st]=1;//算环的长度 q.push(st);while(!q.empty()){int tmp=q.front();q.pop();for(int i=0;i<g[tmp].size();i++){if(dis[g[tmp][i]]) continue;//算过了 if(tmp==st&&g[tmp][i]==ed) continue;//头连尾的那条边 q.push(g[tmp][i]);dis[g[tmp][i]]=dis[tmp]+1;}}cout<<"Yes "<<dis[ed]<<endl;}
}相关文章:

睿抗2024省赛----RC-u4 章鱼图的判断
题目 对于无向图 G(V,E),我们将有且只有一个环的、大于 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。 给定一个无向图,请你判断是不…...

py2exe,一个神奇的 Python 库
在众多Python打包工具中,py2exe无疑是一款出色的选择。它能够将Python脚本转换成可在Windows平台上独立运行的可执行文件,极大地方便了程序的分发与部署。本文将深入探讨py2exe的特性和使用方法,让你在创建桌面应用程序时更加游刃有余。 安装…...

博途PLC网络连接不上
博途PLC网络连接不上其中的一个原因就是网线接触不好,各种原因都试了,任然连接不上,大家可以把网线拔下,重新插拔或者直接更换一根网线。 1、无线网络网段和PLC连接网段冲突 。。。。...

哪个邮箱最安全最好用啊
企业邮箱安全至关重要,需保护隐私、防财务损失、维护通信安全、避免纠纷,并维持业务连续性。哪个企业邮箱最安全好用呢?Zoho企业邮箱,采用加密技术、反垃圾邮件和病毒保护,支持多因素认证,确保数据安全合规…...

企业微信开发智能升级:AIGC技术赋能,打造高效沟通平台
文章目录 一、AIGC在企业微信开发中的核心价值1. 智能化客服体验2. 自动化工作流程3. 个性化内容推荐4. 深度数据分析与洞察 二、使用AIGC进行企业微信开发的实践路径1. 需求分析与场景定义2. 技术选型与平台搭建3. 模型训练与调优4. 接口对接与功能集成5. 测试与优化 《企业微…...
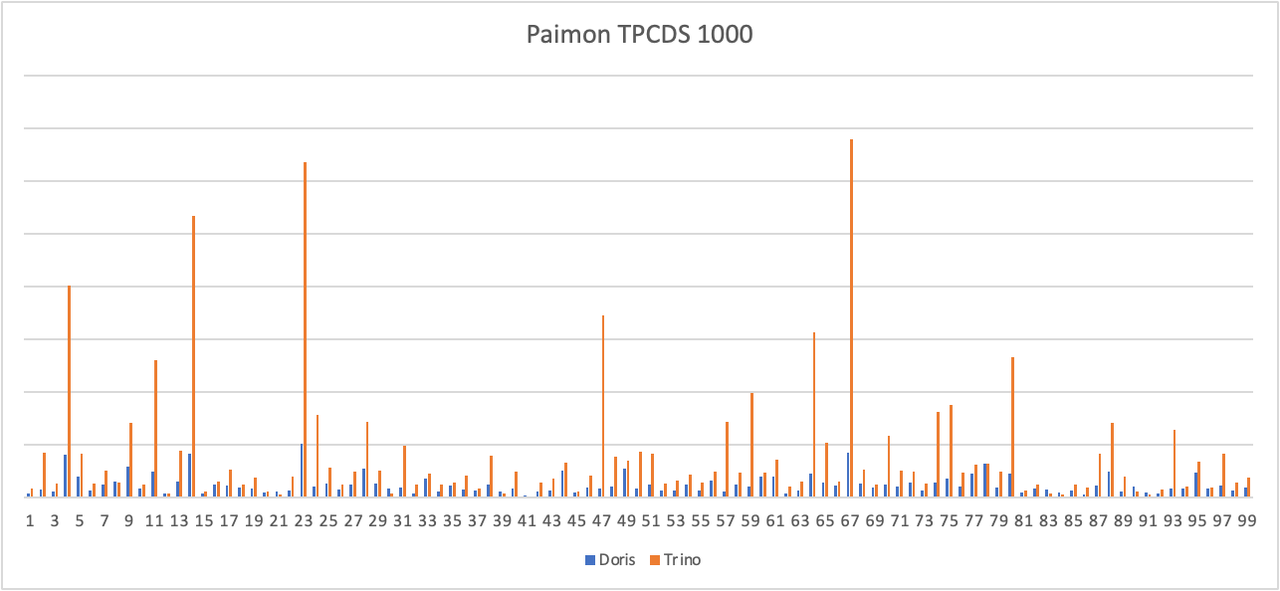
Apache Doris + Paimon 快速搭建指南|Lakehouse 使用手册(二)
湖仓一体(Data Lakehouse)融合了数据仓库的高性能、实时性以及数据湖的低成本、灵活性等优势,帮助用户更加便捷地满足各种数据处理分析的需求。在过去多个版本中,Apache Doris 持续加深与数据湖的融合,已演进出一套成熟…...

Inno setup pascal编码下如何美化安装界面支持带边框,圆角,透明阴影窗口
inno setup自带的安装界面太老套了,如何实现类似网易,微信那种带界面的安装?一般有两种思路:提供一个单独的下载器,然后通过下载器将你用innosetup 打包后的软件下载下来,然后,静默安装这个包&a…...

SQL语句(以MySQL为例)——单表、多表查询
笛卡尔积(或交叉连接): 笛卡尔乘积是一个数学运算。假设我有两个集合 X 和 Y,那么 X 和 Y 的笛卡尔积就是 X 和 Y 的所有可能组合,也就是第一个对象来自于 X,第二个对象来自于 Y 的所有可能。组合的个数即为两个集合中…...

C++第二十八弹---进一步理解模板:特化和分离编译
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1. 非类型模板参数 2. 模板的特化 2.1 概念 2.2 函数模板特化 2.3 类模板特化 2.3.1 全特化 2.3.2 偏特化 2.3.3 类模板特化应用示例 3. …...

正则表达式的独占模式,懒惰模式等有那些区别
正则表达式的独占模式、懒惰模式(也称为非贪婪模式)和贪婪模式(默认模式)在匹配行为上存在显著的区别。以下是这三种模式的详细解释和区别: 1、贪婪模式(Greedy): 默认情况下&…...
】Quartus® Prime Pro Edition 软件 v24.2 中,哪些 Agilex™ 5 IP 功能的硬件验证有限?)
【INTEL(ALTERA)】Quartus® Prime Pro Edition 软件 v24.2 中,哪些 Agilex™ 5 IP 功能的硬件验证有限?
目录 说明 解决方法 说明 如下表所示,Quartus Prime 专业版软件 24.2 版为 Agilex™ 5 IP 或功能提供有限的硬件支持。此外,设备的设备型号、比特流和固件尚未最终确定。 影响 Agilex™ 5 特定功能的已知问题可参阅 Agilex 5 知识库文章搜索。 解决…...

Lua编程
文章目录 概述lua数据类型元表注意 闭包表现 实现 lua/c 接口编程skynet中调用层次虚拟栈C闭包注册表userdatalightuserdata 小结 概述 这次是skynet,需要一些lua/c相关的。写一篇博客,记录下。希望有所收获。 lua数据类型 boolean , number , string…...

2019数字经济公测大赛-VMware逃逸
文章目录 环境搭建漏洞点exp 环境搭建 ubuntu :18.04.01vmware: VMware-Workstation-Full-15.5.0-14665864.x86_64.bundle 这里环境搭不成功。。patch过后就报错,不知道咋搞 发现可能是IDA加载后的patch似乎不行对原来的patch可能有影响,重新下了patch&…...

如何改桥接模式
桥接模式主要是解决 路由功能的 因为NAT多层 主要是网络连接数太多时 然后路由器要好 不然光猫 比差路由要强的 光猫 请注意,对光猫的任何设置进行修改前,请一定要备份光猫的配置文件,并在每次修改前都截图保存原始设置信息!不要…...

江科大/江协科技 STM32学习笔记P13
文章目录 TIM定时中断1、TIM简介计数器PSC预分频器ARR自动重装寄存器 2、定时器类型基本定时器主模式触发DAC 通用定时器高级定时器 3、定时器原理定时中断基本结构预分频器时序计数器时序RCC时钟树 TIM定时中断 1、TIM简介 定时器的基准时钟一般都是主频72MHz,如果…...

loadrunner录制解决提示安全问题
点击页面任意位置,输入: thisisunsafe...

为什么要读写分离?如何实现业务系统读写分离?
信息化水平提升,很多企业已经接受并高频使用多样的业务系统进行日常作业,而在不断的使用过程中,部分行业和业务,如:直播电商、基础制造、公关传媒等,由于自身特点的原因,常常积累了海量的数据。…...

C#基础——类、构造函数和静态成员
类 类是一个数据类型的蓝图。构成类的方法和变量称为类的成员,对象是类的实例。类的定义规定了类的对象由什么组成及在这个对象上可执行什么操作。 class 类名 { (访问属性) 成员变量; (访问属性) 成员函数; } 访问属性:public(公有的&…...

hadoop学习(二)
一.MapReduce 1.1定义:是一个分布式运算程序的编程框架 1.2核心功能:将用户编写的业务逻辑代码和自带默认组件整合成一个完整的分布式运算程序,并发运行在一个Hadoop集群上。 1.3优点 1)易于编程 它简单的实现一些接口&#…...

WXZ196微机消谐装置的运行方式了解一下
WXZ196微机消谐装置是一种用于抑制铁磁谐振的设备,可以在电力系统中快速消除各种频率的铁磁谐振,同时可以区分过电压、铁磁谐振以及单相接地,并给出相应的报警信号。该装置采用高速增强型单片机作为核心元件,对PT开口三角电压进行…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
