【C++题解】1581. 马里奥的银币1
问题:1581. 马里奥的银币1
类型:数组找数
题目描述:
马里奥有很多银币,有一天他得到了一张魔法卡,只要使用这张魔法卡,就可以使得他的银币里面的最大的银币金额变得更大。如果他最大的银币是偶数的金额,可以直接翻倍;如果他最大的银币是奇数的金额,可以使得银币金额加 1 。
比如:假设马里奥存有的银币金额分别为 5 7 8 1 4 ,那么最大的银币面值为 8 ,只要使用魔法卡,银币的金额就会变为5 7 16 1 4 ;
再比如:假设马里奥存有的银币金额分别为 5 7 9 1 4 ,那么最大的银币面值为 9 ,只要使用魔法卡,银币的金额就会变为 5 7 10 1 4 ;
已知马里奥众多的银币中,面额最大的银币只有 1 个,请你求出,马里奥使用魔法卡之后,他的银币金额分别是多少?
输入:
第一行是一个整数 n 代表马里奥有 n 个银币。(n≤1000)
第二行有 n 个整数,用空格隔开,代表马里奥每个银币的金额。
输出:
一行有 n 个整数,代表使用过魔法卡之后,马里奥的银币的金额,分别是多少?
样例:
输入:
5
5 7 8 1 4
输出:
5 7 16 1 4

完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int a[1010];
int main(){//一、分析问题//已知:有 n 个银币。(n≤1000)//未知:使用过魔法卡之后,银币的金额,分别是多少?//关系: 如果他最大的银币是偶数的金额,可以直接翻倍;如果他最大的银币是奇数的金额,可以使得银币金额加 1 。//二、定义变量(已知、未知、关系)int n,mmax=INT_MIN,imax; //三、输入已知cin>>n;for(int i=0;i<n;i++){cin>>a[i];if(a[i]>mmax){mmax=a[i];imax=i;}}//四、根据关系计算if(mmax%2==0){a[imax]+=a[imax];}else{a[imax]+=1;}//五、输出未知 for(int i=0;i<n;i++){cout<<a[i]<<" ";}return 0;
}
相关文章:

【C++题解】1581. 马里奥的银币1
问题:1581. 马里奥的银币1 类型:数组找数 题目描述: 马里奥有很多银币,有一天他得到了一张魔法卡,只要使用这张魔法卡,就可以使得他的银币里面的最大的银币金额变得更大。如果他最大的银币是偶数的金额&a…...

system和popen函数的异同点
system和popen函数的异同点 文章目录 system和popen函数的异同点1.什么是shell命令2.system 函数3.popen 函数4.总结 1.什么是shell命令 Shell 命令是在类 UNIX 操作系统(包括 UNIX、Linux 和 macOS 等)的 Shell 中执行的指令。Shell 是操作系统的命令行…...

Python小工具之httpstat网络分析
一、简介 Python httpstat是一个基于Python的命令行工具,用于测量HTTP请求的性能和状态信息。它能够向目标服务器发送HTTP请求,并显示详细的统计信息,包括DNS解析时间、建立连接时间、TLS/SSL握手时间、首字节时间、总时间等。这些信息对于排…...

挑战房市预测领头羊:KNN vs. 决策树 vs. 线性回归
挑战房市预测领头羊(KNN,决策树,线性回归) 1. 介绍1.1 K最近邻(KNN):与邻居的友谊1.1.1 KNN的基础1.1.2 KNN的运作机制1.1.3 KNN的优缺点 1.2 决策树:解码房价的逻辑树1.2.1 决策树的…...

Docker 基础知识
Docker 基础知识 什么是 Docker? Docker 是一个开源平台,用于开发、发布和运行应用程序。Docker 通过将应用程序及其依赖项打包到一个称为容器的可移植单元中来工作。 Docker 的核心组件是什么? Docker Engine:核心组件࿰…...
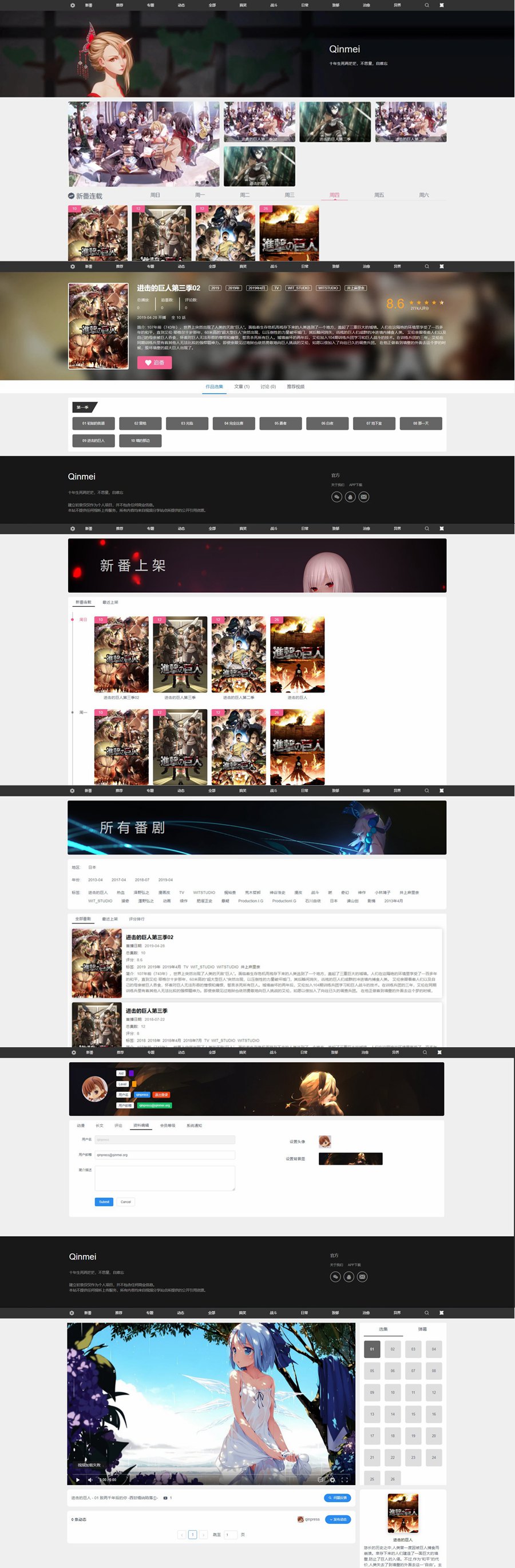
视频主题Qinmei 3.0视频站源码_WordPress影视视频主题/附详细安装教程
Qinmei 3.0主题主要是将 wordpress 改造成纯 api 的站点,以便实现前后端分离的技术栈,目前的进度已经大致完成,唯一的问题就是需要安装 JWT token 插件。 功能介绍: 支持豆瓣以及 bangumi 的一键获取信息, 豆瓣 api 目前使用的是…...

数字看板:跨行业需求下的创新与升级
在当今这个数据驱动的时代,数字看板作为信息展示与决策支持的重要工具,正逐步渗透到各行各业之中。从智慧城市到智能制造,从金融分析到医疗健康,数字看板以其直观、动态、高效的特点,成为了连接数据与决策者的桥梁。本…...

02、爬虫数据解析-Re解析
数据解析的目的是不拿到页面的全部内容,只拿到部分我们想要的内容内容。 Re解析就是正则解析,效率高准确性高。学习本节内容前需要学会基础的正则表达式。 一、正则匹配规则 1、常用元字符 . 匹配除换行符以外的字符 \w 匹配字母或数字或下划…...

掀桌子了!原来是咱们的大屏设计太酷,吓着前端开发老铁了
掀桌子了!原来是咱们的大屏设计太酷,吓着前端开发老铁了 艾斯视觉观点认为:在软件开发的世界里,有时候创意和设计的火花会擦得特别亮,以至于让技术实现的伙伴们感到既兴奋又紧张。这不,我们的设计团队刚刚…...

JavaScriptfor循环的树形菜单栏·
在此声明一下嗷兄弟闷儿!我没写样式纯粹是console.log()打印控制面板的! 全局声明一个data; let data; 然后去获取到json的假数据 let xhr new XMLHttpRequest(); // 设置请求方式和请求地址 xhr.open(get, ./js/menu.json, true); // 发…...

easyExcel 3.x以上版本导入数据后,再把错误信息导出,外加自定义RGB背景色、行高、宽度等
easyExcel 3.x以上版本导入数据后,再把错误信息导出,外加自定义RGB背景色 背景 由于项目中用的easypoi导入的数据量大了,会导致OOM的问题,所以要求更换为easyExcel框架做导入。话不多说,这里只做一个导入的示例&…...

React的img图片路径怎么写
在React中,图片路径的写法取决于你的图片资源是如何被管理和存放的。这里有几种常见的情况和对应的写法: 1. 图片作为React组件的静态资源 如果你的图片文件放在React项目的public文件夹下(这是Create React App项目的默认结构)…...

UGUI优化篇--UGUI合批
UGUI合批 UGUI合批规则概述UGUI性能查看工具合批部分的特殊例子一个白色image、蓝色image覆盖了Text,白色image和Text哪个先渲染 Mask合批Mask为什么会产生两个drawcallMask为什么不能合批Mask注意要点 RectMask2D为什么RecMask2D比Mask性能更好主要代码RectMask2D注…...

FineBI连接MySQL5.7
一、在FineBI系统管理中,点击【新建数据库连接】 选择MySQL数据库 配置数据库连接,如下,其中数据库名称就是需要连接的目标数据库...

基于tkinter的学生信息管理系统之登录界面和主界面菜单设计
目录 一、tkinter的介绍 二、登陆界面的设计 1、登陆界面完整代码 2、部分代码讲解 3、登录的数据模型设计 4、效果展示 三、学生主界面菜单设计 1、学生主界面菜单设计完整代码 2、 部分代码讲解 3、效果展示 四、数据库的模型设计 欢迎大家进来学习和支持!…...

web基础以及http协议
⼀、web基本概念和常识 Web:为⽤户提供的⼀种在互联⽹上浏览信息的服务,Web 服 务是动态的、可交 互的、跨平台的和图形化的。 Web 服务为⽤户提供各种互联⽹服务,这些服务包括信息浏览 服务,以及各种交互式服务,包括…...

DataEase一键部署:轻松搭建数据可视化平台
DataEase是一个开源的数据可视化和分析工具,旨在帮助用户轻松创建和共享数据仪表盘。它支持多种数据源,包括关系型数据库,文件数据源,NoSQL数据库等,提供强大的数据查询、处理和可视化功能。DataEase 不仅是一款数据可…...

网络安全相关竞赛比赛
赛事日历(包含全国所有网络安全竞赛) https://datacon.qianxin.com/competition/competitions https://www.ichunqiu.com/competition/all 全国网络安全竞赛 名称链接全国大学生信息安全竞赛http://www.ciscn.cn/信息安全与对抗技术竞赛(In…...

Vscode——如何快速搜索项目工程中的某个文件的位置
第一步:按 shift ctrl p 第二步:然后把 > 删除 第三步:输入文件名称即可...

Kubernetes 正在弃用 Docker?Docker将何去何从?
一段时间以来,当人们想到容器时,似乎都会想到Docker和Kubernetes。在构建和运行容器方面,Docker 一直是大名鼎鼎的品牌,而在管理和编排容器方面,Kubernetes 一直是大名鼎鼎的品牌。听到 Kubernetes 从 1.20 版开始不再…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

uniapp获取当前位置和经纬度信息
1.1. 获取当前位置和经纬度信息(需要配置高的SDK) 调用uni-app官方API中的uni.chooseLocation(),即打开地图选择位置。 <button click"getAddress">获取定位</button> const getAddress () > {uni.chooseLocatio…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...
