树 形 DP (dnf序)

二叉搜索子树的最大键值
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:class info{public:int maxnum;int minnum;bool isbst;int sum;int maxbstsum;info(int a,int b,bool c,int d,int e){maxnum=a;minnum=b;isbst=c;sum=d;maxbstsum=e;}};info f(TreeNode* root){if(root==nullptr)return info(INT_MIN,INT_MAX,true,0,0);info infol=f(root->left);info infor=f(root->right);int maxn=max(root->val,max(infol.maxnum,infor.maxnum));int minn=min(root->val,min(infol.minnum,infor.minnum));int sumn=root->val+infol.sum+infor.sum;bool isbetn=infol.isbst&&infor.isbst&&root->val<infor.minnum&&root->val>infol.maxnum;int maxbetnumn=max(infol.maxbstsum,infor.maxbstsum);if(isbetn)maxbetnumn=max(maxbetnumn,sumn);return info(maxn,minn,isbetn,sumn,maxbetnumn);}int maxSumBST(TreeNode* root) {return f(root).maxbstsum;}
};递归求从头节点向下的最大的最大子树键值和,而到一个头节点要求其最大的键值和:如果不选头节点,需要子树上的最大键值和;如果选头节点,需要知道子树是否为二叉搜索树和子树所有节点的和,并且还需要子树上的最大值和最小值和头节点比较判断是否可以选头节点。最后把所有需要的信息整合到一起传递给父节点
二叉树的直径
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:class info {public:int height;int diameter;info(int a, int b) {diameter = a;height = b;}};info f(TreeNode* cur) {if (cur == nullptr)return info(0, 0);info infol = f(cur->left);info infor = f(cur->right);int dia = max(infol.diameter, infor.diameter);dia = max(dia, infol.height + infor.height);int hei = max(infol.height, infor.height) + 1;return info(dia, hei);}int diameterOfBinaryTree(TreeNode* root) { return f(root).diameter; }
};从一个头节点及其子树求最大的直径:如果不选头节点,需要其子树的最大直径和;如果选头节点,需要子树的高度
在二叉树中分配金币
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:int ans = 0;int f(TreeNode* root) {if (root == nullptr)return 0;int d = f(root->left) + f(root->right) + root->val - 1;ans += abs(d);return d;}int distributeCoins(TreeNode* root) {f(root);return ans;}
};所有硬币的移动路径之和,是由每条边经过的次数累加和组成,所以只要求出每条边的经过次数求和即可。求一个子树所有边的经过次数之和,需要其子树的所有经过边之和,还有每个子树的节点与其子树上的硬币数量,做差的绝对值就是从头节点的子树到头节点之间的那条边经过的次数
没有上司的舞会
#include <iostream>
#include <vector>
using namespace std;
const int maxn = 6002;
int cnt;
int head[maxn];
int to[maxn];
int nex[maxn];
int happy[maxn];
bool laoda[maxn];
int yes[maxn];
int no[maxn];
void build(int n) {cnt = 1;for (int i = 1; i <= n; i++) {head[i] = 0;happy[i] = 0;laoda[i] = true;yes[i] = 0;no[i] = 0;}
}
void insert(int u, int v) {nex[cnt] = head[u];to[cnt] = v;head[u] = cnt++;
}void f(int cur) {no[cur] = 0;yes[cur] = happy[cur];for (int edge = head[cur]; edge > 0; edge = nex[edge]) {int v = to[edge];f(v);no[cur] += max(no[v], yes[v]);yes[cur] += no[v];}}
int main() {int n;cin >> n;build(n);for (int i = 1; i <= n; i++) {int a;cin >> a;happy[i] = a;}for (int i = 1; i < n; i++) {int a, b;cin >> a >> b;insert(b,a);laoda[a] = false;}int head;for (int i = 1; i <= n; i++)if (laoda[i] == true) {head = i;break;}f(head);cout << max(yes[head], no[head]);return 0;}求一个树的最大快乐值:如果不选头节点,只需要其子树:选子树头节点的最大快乐值和不选子树头节点的最大快乐值;如果选头节点,需要不选子树头节点的最大快乐值
监控二叉树
public class Solution {// 提交如下的方法public int minCameraCover(TreeNode root) {ans = 0;if (f(root) == 0) {ans++;}return ans;}// 遍历过程中一旦需要放置相机,ans++public static int ans;// 递归含义// 假设x上方一定有父亲的情况下,这个假设很重要// x为头的整棵树,最终想都覆盖,// 并且想使用最少的摄像头,x应该是什么样的状态// 返回值含义// 0: x是无覆盖的状态,x下方的节点都已经被覆盖// 1: x是覆盖状态,x上没摄像头,x下方的节点都已经被覆盖// 2: x是覆盖状态,x上有摄像头,x下方的节点都已经被覆盖private int f(TreeNode x) {if (x == null) {return 1;}int left = f(x.left);int right = f(x.right);if (left == 0 || right == 0) {ans++;return 2;}if (left == 1 && right == 1) {return 0;}return 1;}}一个节点的情况:1.没有被监控覆盖 2.被覆盖但没有放监控 3.被覆盖并且放了监控
根据不同的节点情况讨论即可
路径总和
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans;;unordered_map<long ,int>umap;void f(TreeNode* cur,long sum,int targetSum){if(cur==nullptr)return ;sum+=cur->val;long need=sum-targetSum;if(umap.find(need)!=nullptr) ans+=umap[need];umap[sum]++;f(cur->left,sum,targetSum);f(cur->right,sum,targetSum);umap[sum]--;}int pathSum(TreeNode* root, int targetSum) {umap.clear();ans=0;umap[0]=1;f(root,0,targetSum);return ans;}
};树形dp不仅父亲节点需要子节点信息,也可以从父节点向子节点传递信息。求target的路径,如果知道之前遍历过的所有的节点之和,和之前所有从根节点到遍历过的节点的的路径和的路径个数,求出sum-target的路径个数累加即可
到达首都的最少耗油量
public class Solution {public static long minimumFuelCost(int[][] roads, int seats) {int n = roads.length + 1;ArrayList<ArrayList<Integer>> graph = new ArrayList<>();for (int i = 0; i < n; i++) {graph.add(new ArrayList<>());}for (int[] r : roads) {graph.get(r[0]).add(r[1]);graph.get(r[1]).add(r[0]);}int[] size = new int[n];long[] cost = new long[n];f(graph, seats, 0, -1, size, cost);return cost[0];}// 根据图,当前来到u,u的父节点是p// 遍历完成后,请填好size[u]、cost[u]public static void f(ArrayList<ArrayList<Integer>> graph, int seats, int u, int p, int[] size, long[] cost) {size[u] = 1;for (int v : graph.get(u)) {if (v != p) {f(graph, seats, v, u, size, cost);size[u] += size[v];cost[u] += cost[v];// a/b向上取整,可以写成(a+b-1)/b// (size[v]+seats-1) / seats = size[v] / seats 向上取整cost[u] += (size[v] + seats - 1) / seats;}}}}求到达头节点a的最少油量,需要其子树的最少油量,还需要到达其子树的头节点的人的个数,人数对seats求上限加子树的油量就是到达a的最少油量
相邻字符不同的最长路径
class Solution {
public:vector<vector<int>> pragh;void build(int n) {for (int i = 0; i < n; i++)pragh.push_back(vector<int>());}void insert(int u, int v) { pragh[u].push_back(v); }class info {public:int maxhead;int maxleng;info(int a, int b) {maxhead = a;maxleng = b;}};info f(string& s, int cur) {if (pragh[cur].empty())return info(1, 1);int max1 = 0, max2 = 0;int maxheight = 0;for (int edge : pragh[cur]) {info rem = f(s, edge);maxheight = max(maxheight, rem.maxleng);if (s[cur] != s[edge]) {if (rem.maxhead > max1) {max2 = max1;max1 = rem.maxhead;} else if (rem.maxhead > max2) {max2 = rem.maxhead;}}}maxheight = max(maxheight, max1 + max2 + 1);int maxn = max1 + 1;return info(maxn, maxheight);}int longestPath(vector<int>& parent, string s) {int n = parent.size();build(n);for (int i = 1; i < n; i++) {insert(parent[i], i);}return f(s, 0).maxleng;}
};求头节点a的子树的最大路径:如果不选a,需a的子树的最大路径和;如果选a,需要子树的头节点向下延申的最大长度

移除子树后的二叉树高度
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:static const int maxn = 100005;int dfn[maxn];int size[maxn];int deep[maxn];int maxl[maxn];int maxr[maxn];int dfnnum;void f(TreeNode* cur, int k) {int i = ++dfnnum;dfn[cur->val] = i;deep[i] = k;size[i] = 1;if (cur->left != nullptr) {f(cur->left, k + 1);size[i] += size[dfn[cur->left->val]];}if (cur->right != nullptr) {f(cur->right, k + 1);size[i] += size[dfn[cur->right->val]];}}vector<int> treeQueries(TreeNode* root, vector<int>& queries) {dfnnum = 0;f(root, 0);for (int i = 1; i <= dfnnum; i++) {maxl[i] = max(maxl[i - 1], deep[i]);}maxl[0] = 0;maxl[dfnnum + 1] = 0;for (int i = dfnnum; i >= 1; i--)maxr[i] = max(maxr[i + 1], deep[i]);maxr[0] = 0;maxr[dfnnum + 1] = 0;int m = queries.size();vector<int> ans;for (int i = 0; i < m; i++) {int leftmax = maxl[dfn[queries[i]] - 1];int rightmax = maxr[dfn[queries[i]] + size[dfn[queries[i]]]];ans.push_back(max(leftmax, rightmax));}return ans;}
};对树做dfn序,然后求个子树的大小和各节点的高度,并且求出从0到各dfn序节点之间的最大高度和从n到各dfn序节点的最大高度,然后挨个求就可以
从树中删除边的最小分数
class Solution {
public:static const int maxn = 1005;vector<vector<int>> pragh;int dfn[maxn];int size[maxn];int xog[maxn];int dfnnum;void build(int n) {int dfnnum = 0;for (int i = 0; i <= n; i++) {pragh.push_back(vector<int>());dfn[i] = 0;size[0] = 0;xog[i] = 0;}}void insert(int u, int v) {pragh[u].push_back(v);pragh[v].push_back(u);}void f(int cur, vector<int>& nums) {int i = ++dfnnum;dfn[cur] = i;xog[i] = nums[cur];size[i] = 1;for (auto node : pragh[cur]) {if (dfn[node] == 0) {f(node, nums);xog[i] ^= xog[dfn[node]];size[i] += size[dfn[node]];}}}int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {int n = nums.size();build(n);for (auto edge : edges) {insert(edge[0], edge[1]);}f(0, nums);int ans = INT_MAX;for (int i = 0; i < edges.size(); i++) {int a = max(dfn[edges[i][0]], dfn[edges[i][1]]);for (int j = i + 1; j < edges.size(); j++) {int b = max(dfn[edges[j][0]], dfn[edges[j][1]]);int pre, pos;if (a < b) {pre = a;pos = b;} else {pre = b;pos = a;}int sum1 = xog[pos];int sum2, sum3;if (pre + size[pre] > pos) {sum2 = sum1 ^ xog[pre];sum3 = xog[pre] ^ xog[1];} else {sum2 = xog[pre];sum3 = sum1 ^ sum2 ^ xog[1];}ans = min(ans, max(sum1, max(sum2, sum3)) -min(sum1, min(sum2, sum3)));}}return ans;}
};求出各子树的异或和,然后两次for循环枚举各边
选课
三维树形dp,枚举最右子树的分配节点个数讨论
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;// 普通解法,邻接表建图 + 相对好懂的动态规划
// 几乎所有题解都是普通解法的思路,只不过优化了常数时间、做了空间压缩
// 但时间复杂度依然是O(n * 每个节点的孩子平均数量 * m的平方)
public class Main {public static int MAXN = 301;public static int[] nums = new int[MAXN];public static ArrayList<ArrayList<Integer>> graph;static {graph = new ArrayList<>();for (int i = 0; i < MAXN; i++) {graph.add(new ArrayList<>());}}public static int[][][] dp = new int[MAXN][][];public static int n, m;public static void build(int n) {for (int i = 0; i <= n; i++) {graph.get(i).clear();}}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));while (in.nextToken() != StreamTokenizer.TT_EOF) {// 节点编号从0~nn = (int) in.nval;in.nextToken();m = (int) in.nval + 1;build(n);for (int i = 1, pre; i <= n; i++) {in.nextToken();pre = (int) in.nval;graph.get(pre).add(i);in.nextToken();nums[i] = (int) in.nval;}out.println(compute());}out.flush();out.close();br.close();}public static int compute() {for (int i = 0; i <= n; i++) {dp[i] = new int[graph.get(i).size() + 1][m + 1];}for (int i = 0; i <= n; i++) {for (int j = 0; j < dp[i].length; j++) {for (int k = 0; k <= m; k++) {dp[i][j][k] = -1;}}}return f(0, graph.get(0).size(), m);}// 当前来到i号节点为头的子树// 只在i号节点、及其i号节点下方的前j棵子树上挑选节点// 一共挑选k个节点,并且保证挑选的节点连成一片// 返回最大的累加和public static int f(int i, int j, int k) {if (k == 0) {return 0;}if (j == 0 || k == 1) {return nums[i];}if (dp[i][j][k] != -1) {return dp[i][j][k];}int ans = f(i, j - 1, k);// 第j棵子树头节点v int v = graph.get(i).get(j - 1);for (int s = 1; s < k; s++) {ans = Math.max(ans, f(i, j - 1, k - s) + f(v, graph.get(v).size(), s));}dp[i][j][k] = ans;return ans;}}定义"最优子结构",从大的dfn序到小的dfn序推出转移方程
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;
public class Main {public static int MAXN = 301;public static int[] nums = new int[MAXN];// 链式前向星建图public static int edgeCnt;public static int[] head = new int[MAXN];public static int[] next = new int[MAXN];public static int[] to = new int[MAXN];// dfn的计数public static int dfnCnt;// 下标为dfn序号public static int[] val = new int[MAXN + 1];// 下标为dfn序号public static int[] size = new int[MAXN + 1];// 动态规划表public static int[][] dp = new int[MAXN + 2][MAXN];public static int n, m;public static void build(int n, int m) {edgeCnt = 1;dfnCnt = 0;Arrays.fill(head, 0, n + 1, 0);Arrays.fill(dp[n + 2], 0, m + 1, 0);}public static void addEdge(int u, int v) {next[edgeCnt] = head[u];to[edgeCnt] = v;head[u] = edgeCnt++;}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));while (in.nextToken() != StreamTokenizer.TT_EOF) {n = (int) in.nval;in.nextToken();m = (int) in.nval;build(n, m);for (int i = 1; i <= n; i++) {in.nextToken();addEdge((int) in.nval, i);in.nextToken();nums[i] = (int) in.nval;}out.println(compute());}out.flush();out.close();br.close();}public static int compute() {f(0);// 节点编号0 ~ n,dfn序号范围1 ~ n+1// 接下来的逻辑其实就是01背包!不过经历了很多转化// 整体的顺序是根据dfn序来进行的,从大的dfn序,遍历到小的dfn序// dp[i][j] : i ~ n+1 范围的节点,选择j个节点一定要形成有效结构的情况下,最大的累加和// 怎么定义有效结构?重点!重点!重点!// 假设i ~ n+1范围上,目前所有头节点的上方,有一个总的头节点// i ~ n+1范围所有节点,选出来j个节点的结构,// 挂在这个假想的总头节点之下,是一个连续的结构,没有断开的情况// 那么就说,i ~ n+1范围所有节点,选出来j个节点的结构是一个有效结构for (int i = n + 1; i >= 2; i--) {for (int j = 1; j <= m; j++) {dp[i][j] = Math.max(dp[i + size[i]][j], val[i] + dp[i + 1][j - 1]);}}// dp[2][m] : 2 ~ n范围上,选择m个节点一定要形成有效结构的情况下,最大的累加和// 最后来到dfn序为1的节点,一定是原始的0号节点// 原始0号节点下方一定挂着有效结构// 并且和补充的0号节点一定能整体连在一起,没有任何跳跃连接// 于是整个问题解决return nums[0]+dp[2][m];}// u这棵子树的节点数返回public static int f(int u) {int i = ++dfnCnt;val[i] = nums[u];size[i] = 1;for (int ei = head[u], v; ei > 0; ei = next[ei]) {v = to[ei];size[i] += f(v);}return size[i];}}相关文章:

树 形 DP (dnf序)
二叉搜索子树的最大键值 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(null…...

React的生命周期?
React的生命周期分为三个主要阶段:挂载(Mounting)、更新(Updating)和卸载(Unmounting)。 1、挂载(Mounting) 当组件实例被创建并插入 DOM 时调用的生命周期方法&#x…...
c# - - - ASP.NET Core 网页样式丢失,样式不对
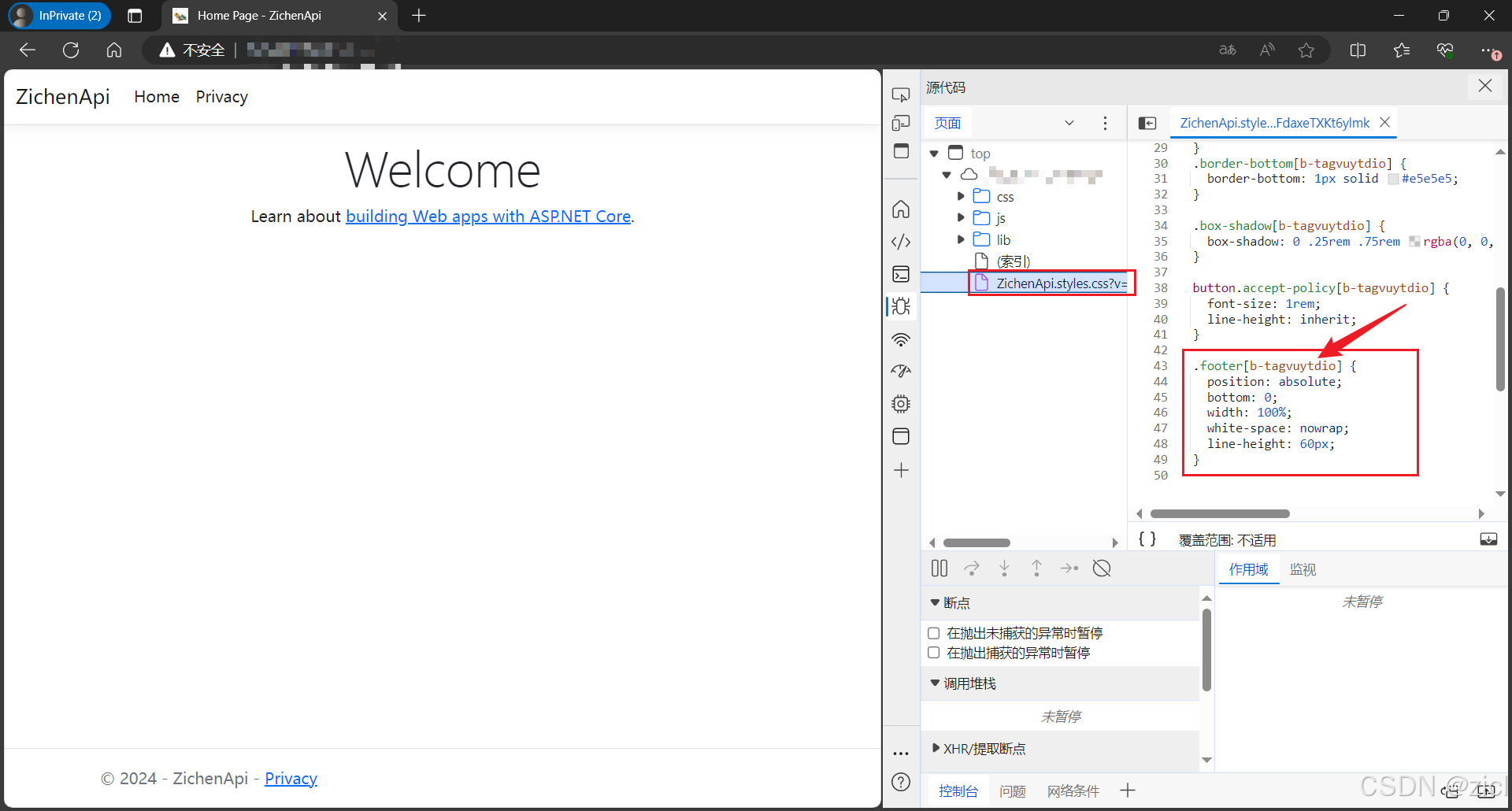
c# - - - ASP.NET Core 网页样式丢失,样式不对 问题 正常样式是这样的。 修改项目名后,样式就变成这样了。底部的内容跑到中间了。 解决 重新生成解决方案,然后发布网站。 原因: 修改项目名之前的 div 上有个这个自定义属…...

Cannot find module ‘html-webpack-plugin
当你在使用Webpack构建项目时遇到Cannot find module html-webpack-plugin这样的错误,这意味着Webpack在构建过程中找不到html-webpack-plugin模块。要解决这个问题,你需要确保已经正确安装了html-webpack-plugin模块,并且在Webpack配置文件中…...

vue、react部署项目的 hashRouter 和 historyRouter模式
Vue 项目 使用 hashRouter 如果你使用的是 hashRouter,通常不需要修改 base,因为 hashRouter 使用 URL 的哈希部分来管理路由,这部分不会被服务器处理。你只需要确保 publicPath 设置正确即可。 使用 historyRouter 如果你使用的是 histo…...

Qt 实现抽屉效果
1、实现效果和UI设计界面 2、工程目录 3、mainwindow.h #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QToolButton> #include <QPushButton> #include <vector> using namespace std;QT_BEGIN_NAMESPACE namespace…...

windows上启动Kafka
官网下载 如:kafka_2.13-2.4.0.tgz 新版集成了Zookeeper ,无需另行下载 解压 至D:\Kafka\kafka_2.13-2.4.0 下 配置Kafka(可跳过) Zookeeper配置 kafka\config\zookeeper.properties下修改dataDir路径(Zookeeper数据目录)dataDirD:\\Program…...

贪心系列专题篇三
目录 单调递增的数字 坏了的计算器 合并区间 无重叠区间 用最少数量的箭 声明:接下来主要使用贪心法来解决问题!!! 单调递增的数字 题目 思路 如果我们遍历整个数组,然后对每个数k从[k,0]依次遍历寻找“单调递…...

Java中两个集合取差集
Java中两个集合取差集 说明: 集合A ListA: search archive relation test 集合B ListB: search search-gejunhao archive-gejunhao archive system 需求: 现在要取存在于A但是不存在B中的元素 test 该如何实现 思路: 在Java中,如果你想要从一个集合ÿ…...

flask mysql数据迁移
flask 数据迁移 在Flask中使用数据库迁移,通常我们会结合SQLAlchemy和Alembic来管理数据库的迁移。以下是一个基本的数据迁移流程: 安装Flask-Migrate: pip install Flask-Migrate 配置Flask应用和数据库: from flask import Fla…...
入门)
Kylin系列(一)入门
Kylin系列(一)入门 目录 简介Kylin的特点安装与配置 环境要求安装步骤 基本概念 Cube维度与度量 Kylin的基本操作 数据准备Cube设计Cube构建查询与分析 最佳实践常见问题总结 简介 Apache Kylin 是一个开源的分布式分析引擎,提供 SQL 查询接口及多维分析&#x…...

pmp学习交流组队~
首先,来看看什么是PMP PMP指的是项目管理专业人士资格认证。它是由美国项目管理协会(Project Management Institute(PMI)发起的,严格评估项目管理人员知识技能是否具有高品质的资格认证考试。 pmp备考攻略本人推荐的参考资料比较多࿰…...

公司常用的监控软件有哪些?2024年六大公司监控软件良心推荐!
在现代企业管理中,监控软件不仅可以帮助提高员工生产力,还可以确保企业数据的安全和保护。小编分享六款公司监控软件,能够满足不同企业的需求,提升管理效率和信息安全。 一、值得推荐的监控软件 1. 固信软件 固信软件https://ww…...

DNS解析异常--排查验证
目录 1.脚本 2.解析结果 3.脚本详解 1.脚本 for j in {1..100}; do for i in $domain1 $domain2; do echo $i; dig $i $dns服务器1 short; sleep 1; dig $i $dns服务器2 short ; sleep 1; done; sleep 2; done; 2.解析结果 ## 域名的解析实际IP: ## $domain1 $IP1 ## $do…...

OpenCV库学习之Canny边缘检测模块
OpenCV库学习之Canny边缘检测模块 一、简介 Canny边缘检测是OpenCV库中一个非常著名的边缘检测算法模块,由John F. Canny在1986年提出。该算法通过多个步骤来确定图像中的边缘,包括噪声降低、梯度计算、非极大值抑制、双阈值检测和边缘跟踪等。Canny边缘…...

Python 教程(七):match...case 模式匹配
目录 专栏列表前言基本语法match 语句case 语句 模式匹配的类型示例具体值匹配类型匹配序列匹配星号表达式命名变量复杂匹配 模式匹配的优势总结 专栏列表 Python教程(一):环境搭建及PyCharm安装Python 教程(二)&…...

Python小项目实战:杨辉三角
题目要求 编写python程序,实现输入正整数n,输出一个n层的杨辉三角,要求打印显示的时候左右对称 比如,输入7,返回结果如图所示 解决思路 generate_pascals_triangle(n) 函数: 生成一个包含 n 层的杨辉三角。 初始化第…...
)
java注解与反射(非常详细, 带有很多样例)
下面是详细地讲解 Java 中的注解与反射,并提供了很多的示例来帮助理解。 Java 注解(Annotations) 1. 注解的基本概念 注解(Annotation)是 Java 5 引入的一种用于为代码元素(类、方法、字段、参数等&…...
模拟实现短信登录功能 (session 和 Redis 两种代码实例) 带前端演示
目录 整体流程 发送验证码 短信验证码登录、注册 校验登录状态 基于 session 实现登录 实现发送短信验证码功能 1. 前端发送请求 2. 后端处理请求 3. 演示 实现登录功能 1. 前端发送请求 2. 后端处理请求 校验登录状态 1. 登录拦截器 2. 注册拦截器 3. 登录完整…...

C# Parallel设置最大并发度
背景 以前用Parallel都是直接用,今天在处理pdf时发现不是很快,特别是有时居然卡死了,异常是有处理的,但没有爆出来,不知道问题在哪。 老老实实不用多线程,一个多小时觉得还是太累。 用的话,部…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
