CS224W—03 GNN

CS224W—03 GNN

回顾

快速回顾一下上一讲的内容。我们学到的关键概念是节点嵌入（Node Embedding）。我们的直觉是将网络中的节点编码到低维向量空间中。我们希望学习一个接受输入图的函数 $f$，并将其嵌入到低维节点嵌入空间中。在这里，我们投影到二维。图机器学习的关键问题是如何定义这个函数 $f$。

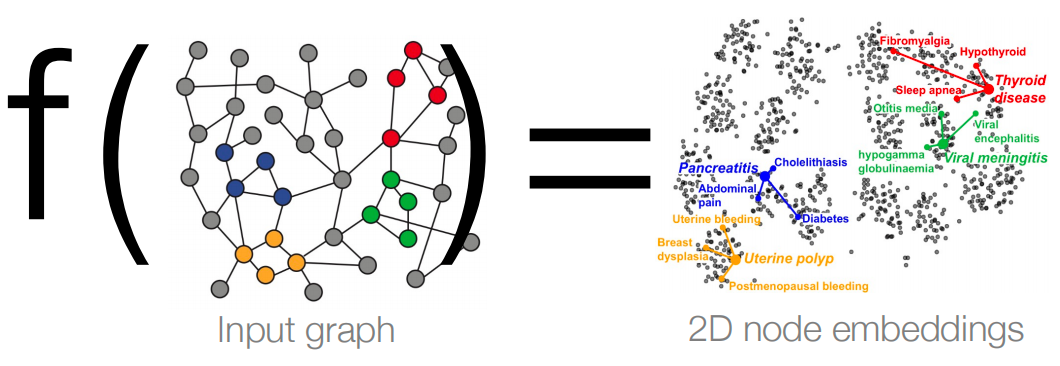
我们如何对节点进行编码？目标是定义一个可以表示网络中相似性的相似函数，并在嵌入空间中进行近似。我们需要定义两件事：相似度函数 $similarity(\cdot )$ 和编码器函数 $ENC(\cdot )$。相似度函数表示网络中两个节点的接近程度，而编码器函数则告诉我们如何将图中的节点映射到嵌入空间。

我们如何定义相似度？上一讲中，我们讨论了基于随机游走的相似度函数。例如，假设两个节点在短随机游走中同时出现，那么我们认为这两个节点是相似的。

我们已经看到了对节点进行编码的最简单方法之一，即通过shallow-encoder查找。在这个浅层编码器中，我们有嵌入矩阵，嵌入矩阵的一列代表一个节点。嵌入矩阵的维数表示节点嵌入的大小。

然而，这种浅层编码器存在一些问题。

• 复杂度为$O(|V|d)$：首先，编码节点的方式并不是真正可扩展的，因为我们需要为每个节点分配一个可学习的向量。这将导致大量的参数，不适用于现实世界的大图。
• 这种方法是推导性的（transductive），只能应用于训练期间见过的节点。这意味着如果出现一个新节点，我们不知道如何编码该新节点，因为它甚至不在嵌入矩阵中。
• 没有包含节点特征。在现实世界的图中，属性或节点特征通常非常有价值。例如，在蛋白质相互作用图中，我们有很多可以与给定节点关联的蛋白质属性。如果没有这个属性，我们将无法从网络中进行有意义的学习。

本节中，我们将定义多层神经网络转换，并使用该深度神经网络对图中的节点进行编码，而不是使用嵌入查找。

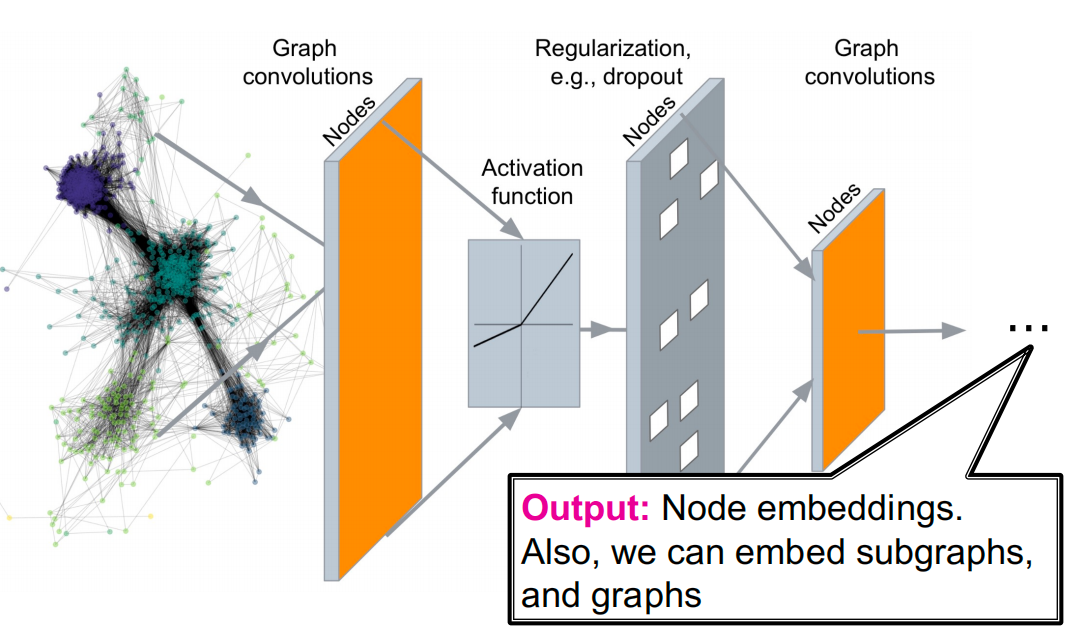
假设我们有了这个编码器，我们能做什么呢？

• 节点分类（Node classfication）。例如，假设我们有一个药物蛋白质相互作用网络，然后我们可以预测这种药物是否有毒，或者是否可以用于治疗特定的疾病。
• 链接预测（Link prediction）。链接预测对于推荐系统来说非常有用，我们可以在其中定义用户和项目之间的交互网络。我们可以预测用户是否会购买某种商品。
• 社区检测（Community detection）。这对于金融网络来说非常有用，因为那里可能存在一群欺诈者，他们之间可能有一些可疑的交易。我们的目标是检测网络中的此类异常集群。
• 网络相似性（Network similarity）。在这种情况下，它将是图级任务或图级预测。例如，我们可以利用这个想法来编码不同的药物分子。所以在这里，我们将分子视为一个网络，我们想要对不同类型的分子进行分类。

Deep Learning for Graphs

Setup

有一个图$G$：

• $V$ 是顶点集合

• $A$ 是邻接矩阵（假设为二进制）

• $\mathbf{X}\in {\mathbb{R}}^{|V|\times m}$ 为节点特征矩阵

• $v$：$V$中的一个节点：$N(v)$：节点$v$的邻居集合。

• 节点特征：

  • 社交网络：用户档案，用户图片

  • 生物网络：基因表达谱，基因功能信息

  • 当图中数据集没有节点特征时：

    • 指示向量（节点的one-hot编码）

    • 常数向量：$[1,1,\dots ,1]$

A Naive Approach

简单的想法：将邻接矩阵和特征合并在一起应用在深度神经网络上（如图，直接一个节点的邻接矩阵+特征合起来作为一个输入）。这种方法的问题在于：

• 需要 $O(|V|)$ 的参数
• 不适用于不同大小的图
• 对节点顺序敏感。

排列不变性与同变性

利用image卷积的思想，扩展到graph上。现实世界的图上无法定义固定的locality或滑动窗口，而且图是permutation invariant的，没有规范的排列顺序。

• Permutation Invariant 用于全局图表示，确保输出与节点排列无关。
• Permutation Equivariant 用于节点级别表示，确保输出在节点排列变化时按相同方式变化。

Permutation Invariant（排列不变性）：

排列不变性通常指的是模型对节点特征的排列顺序不敏感。这意味着无论节点特征的顺序如何变化，只要特征值本身保持不变，模型的输出也应该保持不变。

$$f(A_1,X_1)=f(A_2,X_2)$$
对于任意排列$P$：$f(A,X)=f(PA{P}^T,PX)$

比如
f ( { 1 , 2 , 3 } ) = [ 1 , 2 , 3 ] f ( { 2 , 1 , 3 } ) = [ 1 , 2 , 3 ] f(\{1,2,3\})=[1,2,3]\\ f(\{2,1,3\})=[1,2,3] f({1,2,3})=[1,2,3]f({2,1,3})=[1,2,3]

Permutation Equivariant（排列同变性）：

如果图的节点排列发生变化，那么模型的输出会按相同的方式重新排列。这在处理图中每个节点的表示（如节点分类任务）时非常重要。

对于任意排列$P$：$Pf(A,X)=f(PA{P}^T,PX)$

比如：
f ( { 1 , 2 , 3 } ) = [ 1 , 2 , 3 ] f ( { 2 , 1 , 3 } ) = [ 2 , 1 , 3 ] f(\{1,2,3\})=[1,2,3]\\ f(\{2,1,3\})=[2,1,3] f({1,2,3})=[1,2,3]f({2,1,3})=[2,1,3]

GCN

思想：基于节点的邻居定义一个计算图；通过学习图的传播信息来计算节点特征。

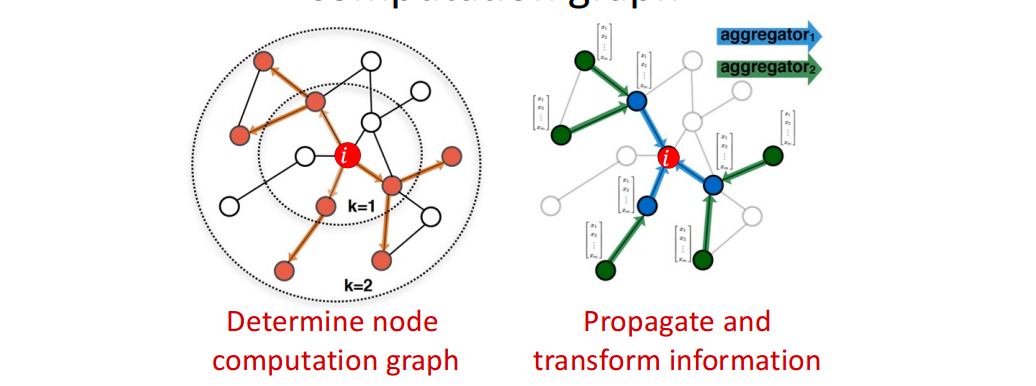
Aggregate Neighbors

核心思想：基于局部的网络邻居产生节点嵌入。

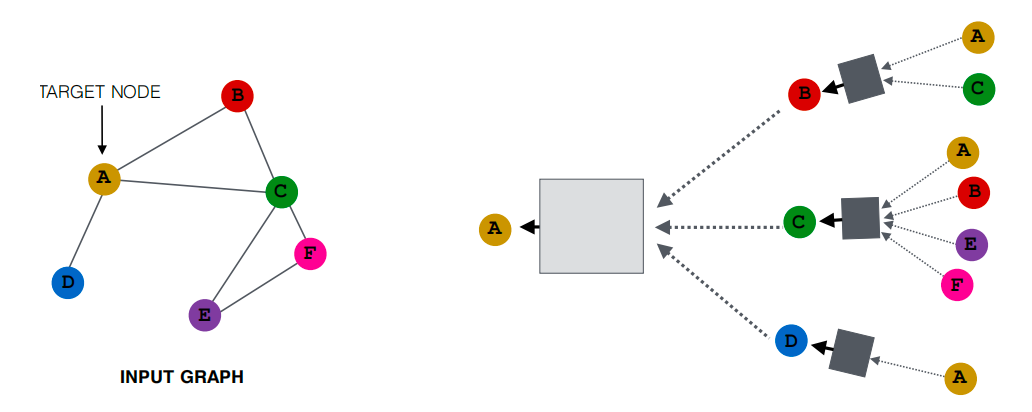
以上图为例，我们想要对节点A进行编码。我们将通过查找 A 在网络中的直接邻居 B、C 和 D 来获得计算图。然后我们将迭代地为其每个邻居计算邻居结构。因此，对于节点 B，我们将看到其邻居 A 和 C。对于节点 C，我们将看到其邻居ABEF，依此类推。这种展开可以迭代地发生，直到达到希望看到的轮数。这就是网络中的层数。

需要注意的事情是一个节点可以在此计算图中出现多次。

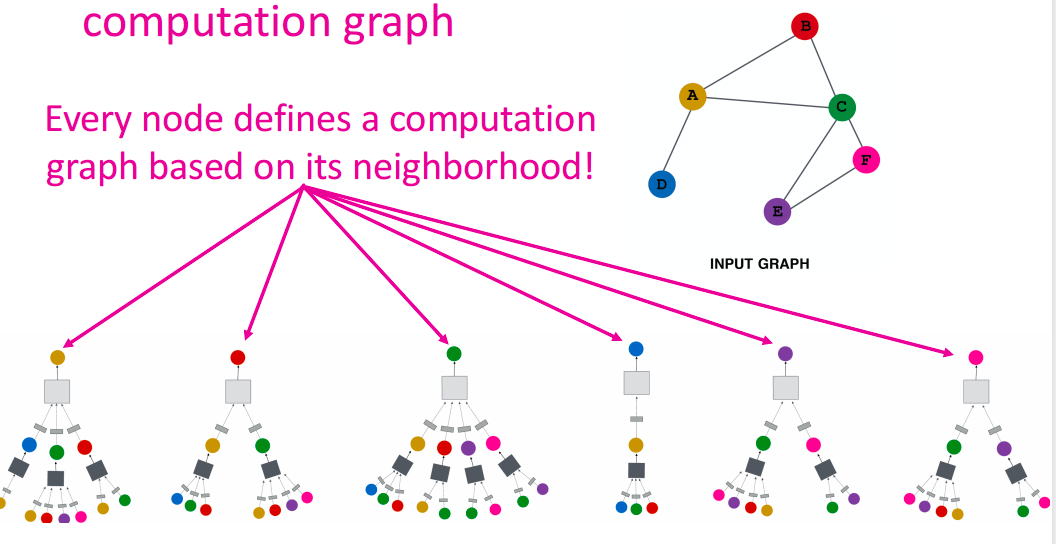
而这种深度模型就是有很多层

• 每个层的节点都有嵌入
• 第$k$层嵌入获取来自$k$跳距离节点的信息
• 

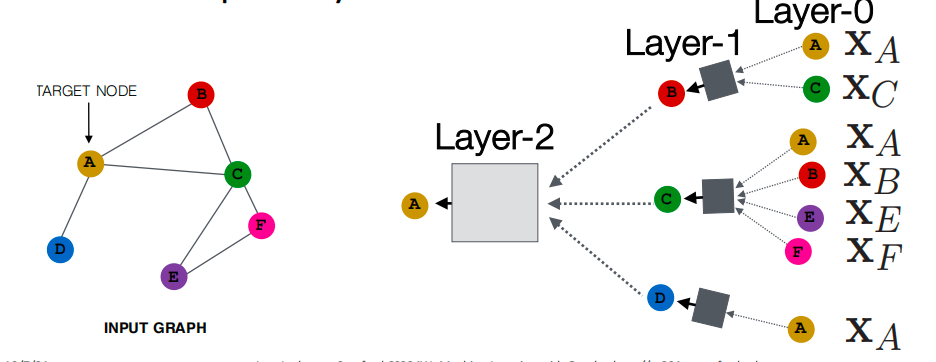
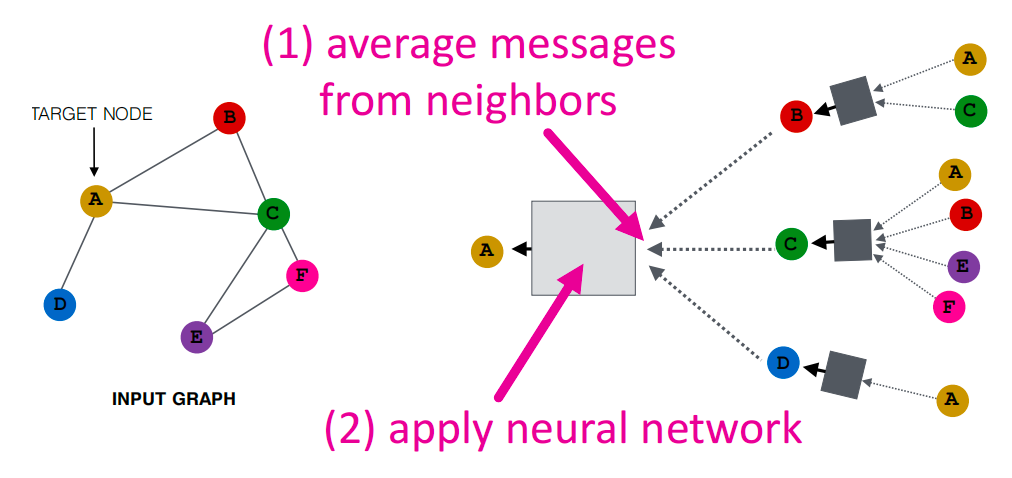
如何聚合邻居的信息：平均邻居信息，然后应用神经网络

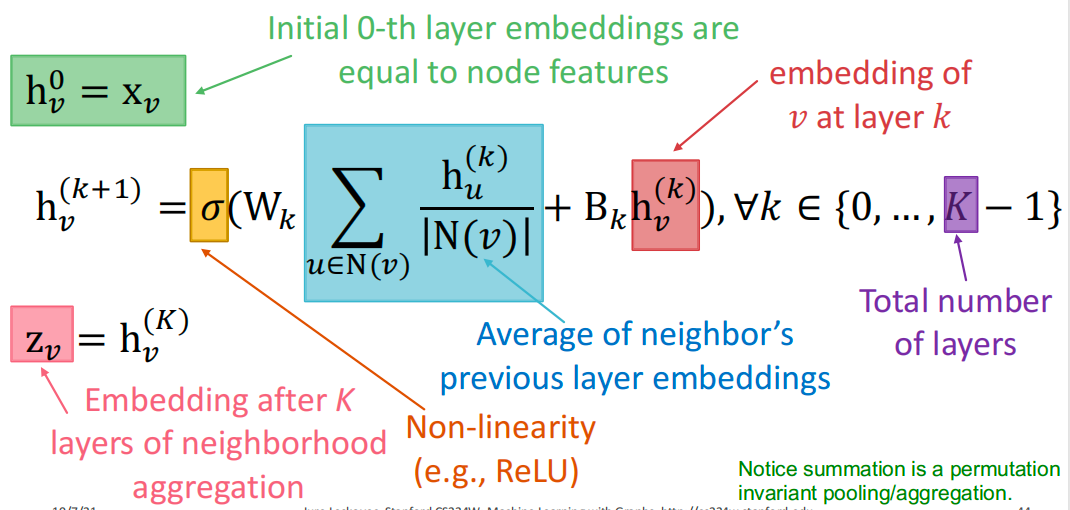
GCN: invariance and equivariance

给定一个节点，计算其embedding是置换不变的

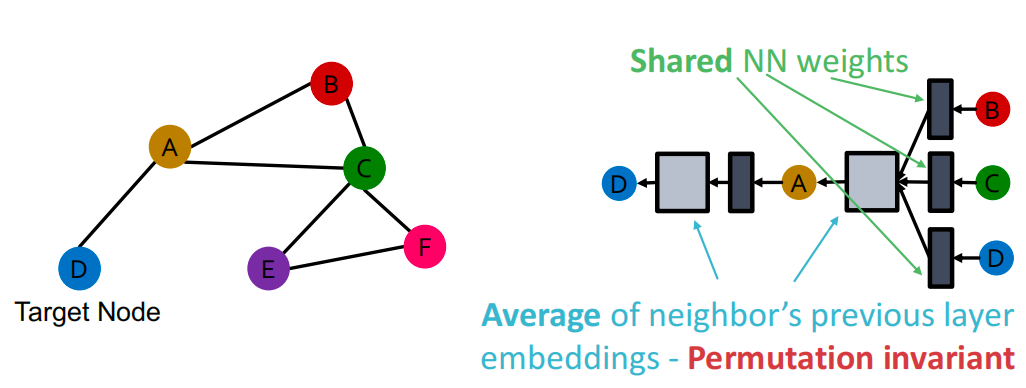
如果考虑图中的所有节点，GCN的计算是置换同变的：

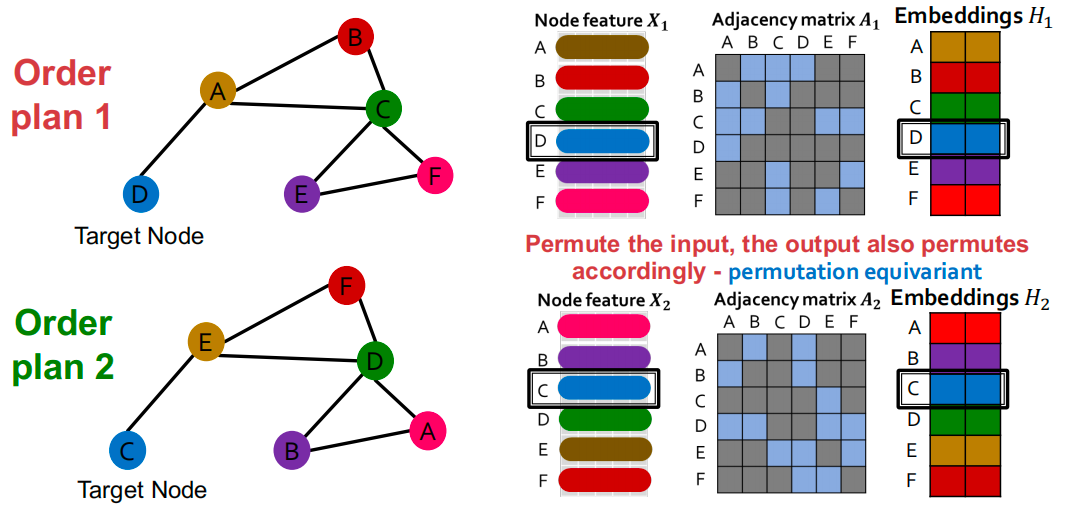
1. 输入节点特征的行与输出嵌入的行对齐：

   • 这意味着在输入特征矩阵中，每个节点的特征行与在输出嵌入矩阵中的相应行是一一对应的。换句话说，如果我们有一个节点特征矩阵，其中每一行代表一个节点的特征，那么在经过GCN处理后，输出嵌入矩阵中的每一行也将代表同一个节点的嵌入。

2. GCN计算给定节点的嵌入是不变的：

   • 这意味着无论输入特征矩阵如何排列，只要节点的特征值不变，GCN计算出的该节点的嵌入也将保持不变。这是GCN排列不变性的表现。

3. 排列后，给定节点在输入特征矩阵中的位置变了，但输出嵌入保持相同：

   • 当输入特征矩阵的行（即节点特征）被重新排列后，该节点在矩阵中的位置会发生变化。然而，由于GCN的排列不变性，该节点的输出嵌入不会改变。这意味着无论输入特征的排列顺序如何，输出嵌入矩阵中相应节点的嵌入都将保持一致。

4. 例如C和D的位置一样，节点特征一样，输入的位置不一样，那么输出的嵌入一样（排列不变性），位置不一样（排列同变性）。

模型训练

模型的参数定义如下：

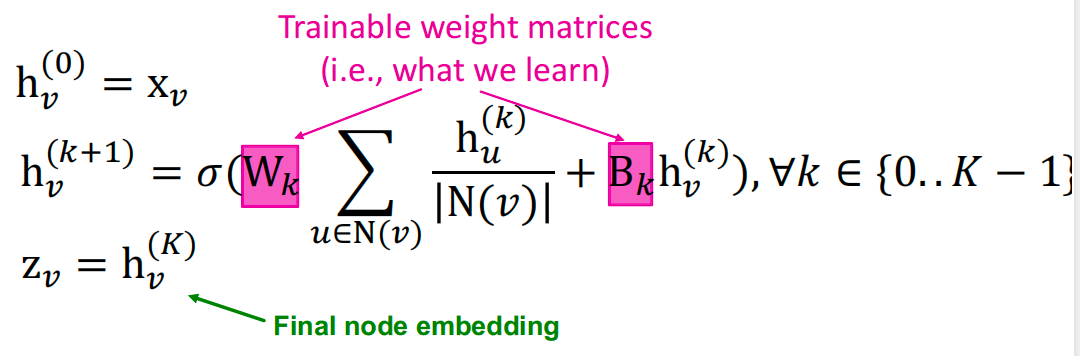
我们可以将这些嵌入输入到任何损失函数中，并运行SGD来训练权重参数：

• $h_k$：节点$v$在第$k$层的隐藏表示
• $W_k$：用于邻域聚合的权重矩阵
• $B_k$：用于转换自身隐藏向量的权重矩阵

矩阵化

可以通过（稀疏）矩阵操作高效执行许多聚合：

• 隐藏嵌入矩阵 $H^{(k)}=[h_1^{(k)}\cdots h_{|V|}^{(k)}]$
• 然后：${\sum }_{u\in N_v}{h}_u^{(k)}=A_{v,:}{H}^{(k)}$
• 设 $D$ 为对角矩阵，其中 $D_{v,u}=\mathrm{deg}(v)=|N(v)|$
• $D$ 的逆矩阵 $D^{-1}$ 也是对角的：$D_{v,u}^{-1}=1/|N(v)|$
• 因此，

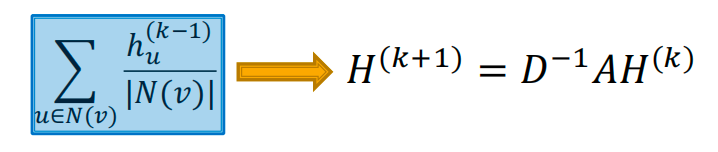
参数更新函数可以重写如下：

当aggregation函数过度复杂时，GNN可能无法被表示成矩阵形式。

训练

节点嵌入${\mathbf{z}}_u$是输入图的函数。

监督设置：我们希望最小化损失$\underset{\Theta }{\min }\mathcal{L}(\mathbf{y},f({\mathbf{z}}_u))$：

• $\mathbf{y}$：节点标签
• 如果 $\mathbf{y}$ 是实数，$\mathcal{L}$可以是$L2$损失；如果 $\mathbf{y}$ 是分类标签，可以是交叉熵损失，。
• 对于节点分类，可以设计如下损失函数：
• 

无监督设置：

• 没有节点标签可用
• 使用图结构作为学习的目标。
• ${\min }_{\mathbf{\Theta }}\mathcal{L}={\sum }_{z_u,z_v}\mathrm{CE}\left(y_{u,v},\mathrm{DEC}(z_u,z_v)\right)$
  • 其实如果u和v相似，则$y_{u,v}=1$
  • $z_u=f_{\Theta }(u)$，$DEC(\cdot )$ 为点积。
  • $\mathrm{CE}(\mathbf{y},f(\mathbf{x}))=-{\sum }_{i=1}^C\left(y_i\log f_{\Theta }(x{)}_i\right))$
• 节点的相似性可以使用上一节学习的随机游走以及矩阵分解来求得。

模型设计

模型设计：

1. 定义邻居聚合函数
2. 定义节点嵌入上的损失函数
3. 在节点集合（如计算图的batch）上做训练
4. 训练后的模型可以应用在训练过与没有训练过的节点上

推导能力

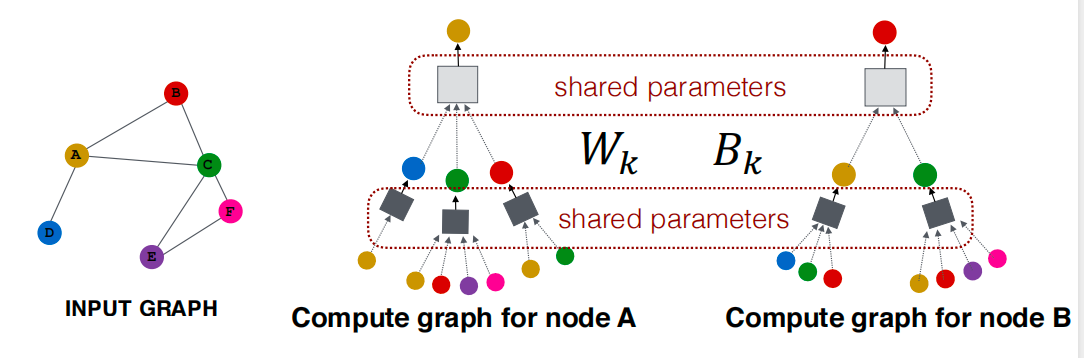
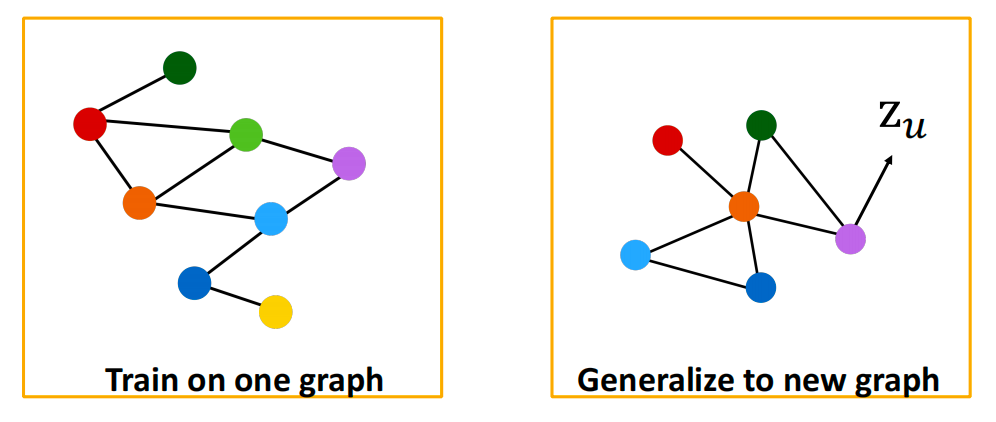
相同的聚合参数被所有节点共享：模型参数的数量与节点数$N$成次线性关系，我们可以推广到未见过的节点。

参考资料

• http://t.csdnimg.cn/Hvhhx
• https://web.stanford.edu/class/cs224w/