数据结构之探索“堆”的奥秘
找往期文章包括但不限于本期文章中不懂的知识点:
个人主页:我要学编程(ಥ_ಥ)-CSDN博客
所属专栏:数据结构(Java版)
目录
堆的概念
堆的创建
时间复杂度分析:
堆的插入与删除
优先级队列
PriorityQueue的特性
PriorityQueue源码分析
PriorityQueue常用接口介绍
构造方法:
堆的应用
堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储(从上到下、从左到右)在 一个一维数组 中,并满足:Ki <= K(2i+1) 且 Ki<=K(2i+2) (Ki >= K(2i+1) 且 Ki >= K(2i+2) ) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
注意:Ki <= K(2i+1) 且 Ki<=K(2i+2) 这个公式就是说明根结点的值小于等于左右孩子节点的值,即小根堆或者最小堆。与其相反就是根结点的值大于等于左右孩子节点,即大根堆或者最大堆。
堆的性质:
1、堆中某个节点的值总是不大于或不小于其父节点的值;
例如:小根堆就是根结点的值小于等于孩子节点的值,也就是说孩子节点的值大于等于根结点的值,也就对应了孩子节点不小于其父节点;反之,就是大根堆的性质了。
2、堆总是一棵完全二叉树。
因为堆是把数据按照完全二叉树的方式存储在一个一维数组中的。
3、堆的根结点总是这个一维数组中的最值,要么是最大值,要么是最小值。
如果是大根堆,按照 性质1 的推论就是:根结点的值大于等于孩子节点的值。这样一直递归下去,根结点肯定就是最大的。最坏情况就是所有结点的值全部相等。
4、堆的存储结构是一个一维数组,但是其逻辑结构是一个完全二叉树。
为什么不能是一个普通的二叉树呢?因为普通的二叉树会有空节点(空树),这样在数组中就会null元素的存在,导致了空间利用率比较低。
堆的创建
现有一组数据 {0,1,2,3,4,5,6,7,8,9} 我们要把这组数据组织成大根堆。
public class Heap {int[] elem;int usedSize;public Heap(int k) {elem = new int[k];}public Heap() {elem = new int[10];}// 给堆初始化数据public void initHeap(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}
}思路:大根堆的特点是根结点的值大于左右孩子节点的值。这里采用的是一种向下调整的方法。
即从最后一棵树的根结点位置开始进行调整大根堆,一直调整到整棵树的根结点满足大根堆。

// 创建大根堆
public void createHeap() {// 从最后一棵子树的根结点位置开始for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {// 向下调整的方法:从要调整的位置开始,到整棵树结束siftDown(parent, usedSize);}
}private void siftDown(int parent, int usedSize) {int child = parent * 2 + 1;// 只有当孩子节点在有效数据之内时,才能调整while (child < usedSize) {// 先找到左右孩子节点的最大值if (child+1 < usedSize && elem[child] < elem[child+1]) { // 得确保右孩子存在child++;}// 比较孩子节点的最大值和根结点的值if (elem[parent] < elem[child]) {// 交换swap(elem, parent, child);// 交换完成只是本级满足了大根堆的条件,但是交换下去的值不一定满足当级的大根堆条件parent = child;child = parent * 2 + 1;} else {// 满足大根堆就不需要继续调整了break;}}
}private void swap(int[] elem, int i, int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;
}这里可能有几个小伙伴们疑惑的地方:
1、为什么交换完成之后还要再进行向下调整判断是否需要交换?

总而言之就是一句话:参与调整的,就得再次进行判断是否符合大根堆。
2、为什么本级满足大根堆的情况后,就不需要继续往下判断是否调整?
因为我们是从下面开始调整的,如果本级满足了大根堆,那么下面的就一定也满足大根堆。因此就无需继续判断了。
时间复杂度分析:

将上面的所有结果相加,就是最终的时间复杂度。

因此向下调整建堆的时间复杂度是:O(N)。
堆的插入与删除
堆的插入:
思路:因为堆在存储上是一个数组,那么我们肯定是按照插入数组元素的方法来进行插入,即尾插。尾插完之后,还得进行判断这个新的堆是否是大根堆。因为这个的判断方式是从插入的节点开始往上判断,因此这个判断是向上调整。
public void offer(int val) {// 插入的元素放到最后,然后其所在的树进行向上调整// 判满,扩容if (isFull()) {elem = Arrays.copyOf(elem, elem.length*2);}elem[usedSize++] = val;siftUp(usedSize-1, 0);}private boolean isFull() {return usedSize == elem.length;}private void siftUp(int child, int end) {// 因为原来是满足大根堆的,因此我们只需要判断这个新插入的元素是否也满足int parent = (child-1) / 2;while (parent >= end) {if (elem[child] > elem[parent]) {// 交换swap(elem, child, parent);child = parent;parent = (child-1) / 2;} else {// 因为原来是满足大根堆的,如果这个也满足,那么就全部满足了break;}}}有了插入方法,我们也就可以通过插入来创建堆了。
注意:我们手动创建堆的方法是采用向下调整,而插入元素采用的是向上调整。因此,两者创建出来的堆结果会不一样,但都是大根堆。
向上调整建堆的时间复杂度分析:
与向下调整相比,向上调整还要把最后一层的节点全部调整,因此,向上调整的时间复杂度肯定是大于向下调整的。

向上调整建堆的时间复杂度O(N+logN) 。
堆的删除:
思路:堆的删除,我们采取的方式也和数组类似,是把堆顶元素与最后一个元素交换,再进行向下调整。
public int poll() {// 判空,抛异常if (isEmpty()) {throw new HeapIsEmptyException("堆为空异常");}int val = elem[0];swap(elem, 0, usedSize-1);siftDown(0, usedSize-1);usedSize--;return val;}private boolean isEmpty() {return usedSize == 0;}堆的删除的时间复杂度:O(logN)。
交换完,向下调整就只调整树的高度,也就是logN。
堆的插入的时间复杂度:O(logN)。
插在最后,然后进行向上调整,也是调整树的高度。
获取堆顶元素:
public int peek() {if (isEmpty()) {throw new HeapIsEmptyException("堆为空异常");}return elem[0];}看到这里,我们就应该可以猜出堆和队列是有关系的,否则,不会把队列的方法名给堆。堆这种数据结构可以实现优先级队列。
优先级队列
通过堆的性质3,我们就可以推出一个结论:如果我们每次从堆中删除数据一定删除的是优先级最高的。如果是小根堆,那么就是删除最小值,如果是大根堆,那么删除的就是最大值。即优先级最高的先被删除。这就对应了队列中的一个特殊队列:优先级队列。实际上JavaAPI中优先级队列底层就是通过堆来实现的。
PriorityQueue的特性
1、使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;2、PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常。
因为堆中的元素是需要可以比较大小。否则,无法判别优先级。
3、不能插入null对象,否则会抛出NullPointerException。
因为我们去比较的时候,是通过对象调用专属的比较方法,如果对象为null,就会发生空指针异常。
4、PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素。
5、其内部可以自动扩容,无需我们主动实现。
PriorityQueue源码分析


PriorityQueue常用接口介绍
构造方法:
| 构造器 | 功能介绍 |
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异常 |
| PriorityQueue(Collection c) | 用一个集合来创建优先级队列 |
使用:
public class Test {public static void main(String[] args) {// 创建一个优先级队列,默认容量11PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>();// 创建一个优先级队列,容量是20PriorityQueue<Integer> priorityQueue2 = new PriorityQueue<>(20);List<Integer> list = new ArrayList<>();list.add(1);list.add(2);list.add(3);list.add(4);list.add(5);// 创建一个优先级队列(容量根据list的大小来分配)PriorityQueue<Integer> priorityQueue3 = new PriorityQueue<>(list);// 长度System.out.println(priorityQueue3.size());// 小根堆System.out.println(priorityQueue3.poll());}
}这里的“容量根据list的大小来分配”的意思是:本来的默认容量是11,如果list的长度大于11,那么就会按照2倍或者1.5倍去扩容。
插入/删除/获取优先级最高的元素
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时间复杂度O(log2 N),注意:空间不够时候会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll () | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
堆的应用
1、PriorityQueue的实现。
2、堆排序。
不同的顺序,建立不同的堆,但是一定是后面的元素先有序,再是前面的元素有序。
因此我们就可以知道:如果是从小到大排序,那么就要建大根堆;反之,则是建小根堆。
因为 如果是从小到大排序,且后面的元素先有序,那么后面的元素只能是最大的,因此建立大根堆的话,堆顶元素一定是最大的。这时,我们只需把堆顶元素和最后一个元素进行交换,然后再进行向下调整,直至调整到整棵树的根节点。
代码实现:
public void heapSort() {int j = 0;for (int i = usedSize-1; i > 0; i--) {swap(elem,i,j);siftDown(0, i);}}3、Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大,且K都比较小。
例如:全球前500强的企业。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
如果是要找前K个最小的元素,将前K个元素建成大根堆,然后再去遍历后N-K个元素,遇到小于堆顶元素的就交换,遍历完成后剩下的堆中元素就是前K个最小的。
练习:面试题 17.14.最小K的个数
题目:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4]提示:
0 <= len(arr) <= 1000000 <= k <= min(100000, len(arr))
思路一:直接排序,然后遍历前K个即可。
public int[] smallestK(int[] arr, int k) {// 调用JavaAPI提供的方法才行,自己实现的方法会超出时间限制Arrays.sort(arr); // 默认是从小到大排序int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = arr[i];}return ret;}
思路二:将N个元素建成小根堆,然后每次取堆顶元素,取K次即可。
public int[] smallestK(int[] arr, int k) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {priorityQueue.offer(arr[i]);}// 上面是建成的小根堆int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}思路三:取前K个元素建成大根堆,然后再遍历剩下的元素,如果小于堆顶元素,则交换。
class Solution {public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];if (k == 0 || arr == null) {return ret;}PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, new Incompare());for (int i = 0; i < k; i++) {priorityQueue.offer(arr[i]);}for (int i = k; i < arr.length; i++) {if (priorityQueue.peek() > arr[i]) {priorityQueue.poll();priorityQueue.offer(arr[i]);}}for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}
}// 创建新的比较器
class Incompare implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
好啦!本期 数据结构之探索“堆”的奥秘 的学习之旅就到此结束啦!我们下一期再一起学习吧!
相关文章:

数据结构之探索“堆”的奥秘
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程(ಥ_ಥ)-CSDN博客 所属专栏:数据结构(Java版) 目录 堆的概念 堆的创建 时间复杂度分析: 堆的插入与删除 优先级队列 PriorityQ…...

光影漫游者:高科技球形场馆开启沉浸式体验新时代—轻空间
轻空间(江苏)膜科技有限公司的自主品牌“QSPACE轻空间”推出的“光影漫游者”,是一款突破传统的创新球形场馆。这款产品自问世以来,以其独特的设计和卓越的功能迅速成为各类活动和展览的焦点。光影漫游者不仅以其时尚的外观吸引了…...

面试题007:static修饰符可以修饰什么,static的重要规则
在Java类中,可用static修饰属性、方法、代码块、内部类 。static关键字修饰的成员被称为静态成员。 被修饰后的成员具备以下特点: 随着类的加载而加载 优先于对象存在 修饰的成员,被所有对象所共享 访问权限允许时,可不创建对…...
EasyTwin的动画系统已经到了next level?快来一探究竟!
在实际的数字孪生项目场景建设中,水利项目中的洪水推演、工业领域的工程施工模拟、车间产线运转、机械装置和零件配置展示等项目场景,都对动画效果有很强的使用需求,这是对渲染软件和设计师能力的极大考验🆘。 别担心!…...

当业务开展遇到阻力,如何开展?
1:先够通问题,看能否通过及时的沟通解决掉问题阻力(相信你已经做过了无功而返) 2:全面思考这个问题,这个事情对方做了对他有什么好处?对大家的公共目标有什么好处?尝试说服 3&#x…...

萨科微半导体整流桥
金航标kinghelm萨科微总经理宋仕强介绍说,萨科微半导体的整流桥热销型号及其主要参数?萨科微的整流桥热销型号有 DB207S,其主要参数有:反向工作电压(VRRM)为 1000V、直流输出电流(Io)为 2.0A、…...

STM32的GPIO输入输出方式设置示例
1、GPIO口做基本的输入/输出口使用时,输入有上拉输入、下拉输入、浮空输入(既无上拉电阻也无下拉电阻)3种输入方式;输出有开漏输出、推挽输出2种输出方式。 2、示例 (1)示例1:GPIO做输出的设置…...

SQL插入、更新和删除数据
SQL插入、更新和删除数据 一、直接向表插入数据 1.1、插入完整的行 这里所说的完整行指的是包含表内所有字段的数据行;假设表中有n个字段,则插入完整行的语法: INSERT INTO 表名或视图名 VALUES(字段1的值,字段2的值,字段3的值,...,字段n的…...

如何将幻灯片中的图片背景设置为透明
在制作幻灯片时,我们经常需要插入图片来丰富内容,提升视觉效果。但有时,图片的背景可能会干扰幻灯片的整体设计,这时将图片背景设置为透明就显得尤为重要。本文将详细介绍如何在常用的幻灯片制作软件中实现这一效果,帮…...

【雅思考试】-- Day2 - 单词
雅思单词 WordPOSDefinitionWordPOSDefinition1reliabilityn.可靠性16facilitatev.促进;助长2goaln.目标17expectationn.期待;期望;预期3strengthn.力量;力气;实力18reinforcen.加强;加固;强化4…...

.\venv\Scripts\activate : 无法加载文件 E:\,因为在此系统上禁止运行脚本。
问题描述: 问题原因: Windows PowerShell 的执行策略用于控制脚本的运行权限和安全性。 以下是几种常见的执行策略及其特点: AllSigned:只允许运行经过数字签名的脚本。这意味着无论是本地创建的还是从网络获取的脚本࿰…...

C++之explicit
在 C 中,explicit 是一个关键字,用于修饰单参数的构造函数,防止它们被用于隐式类型转换。理解 explicit 关键字涉及以下几个方面: 1. 隐式类型转换 在 C 中,单参数的构造函数可以被用于执行隐式类型转换,…...
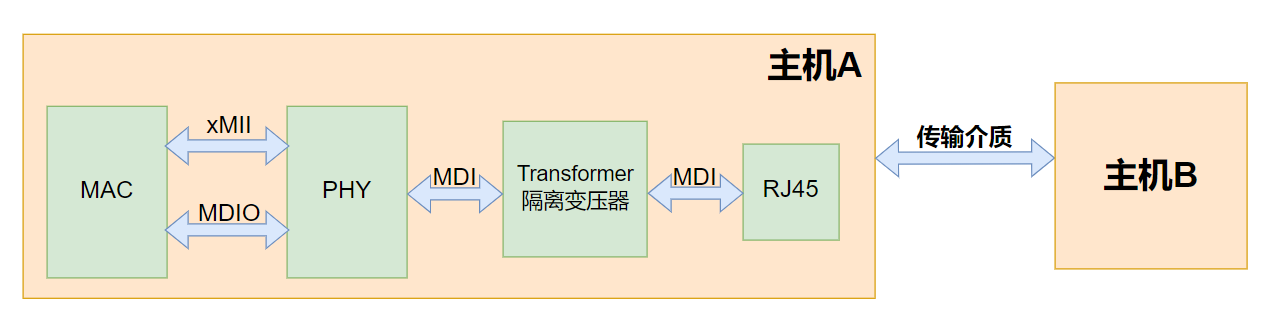
基于FPGA的以太网设计(4)----详解PHY的使用(以YT8531为例)
目录 1、前言 2、如何了解PHY芯片? 2.1、总览 2.2、管脚 2.3、编码 2.4、自协商 2.5、环回模式 2.6、睡眠模式 2.7、复位 2.8、PHY地址 3、PHY芯片的寄存器配置 3.1、Basic Control Register (0x00) 3.2、Basic StatusRegister (0x01) 3.3、PHY Specific Status…...
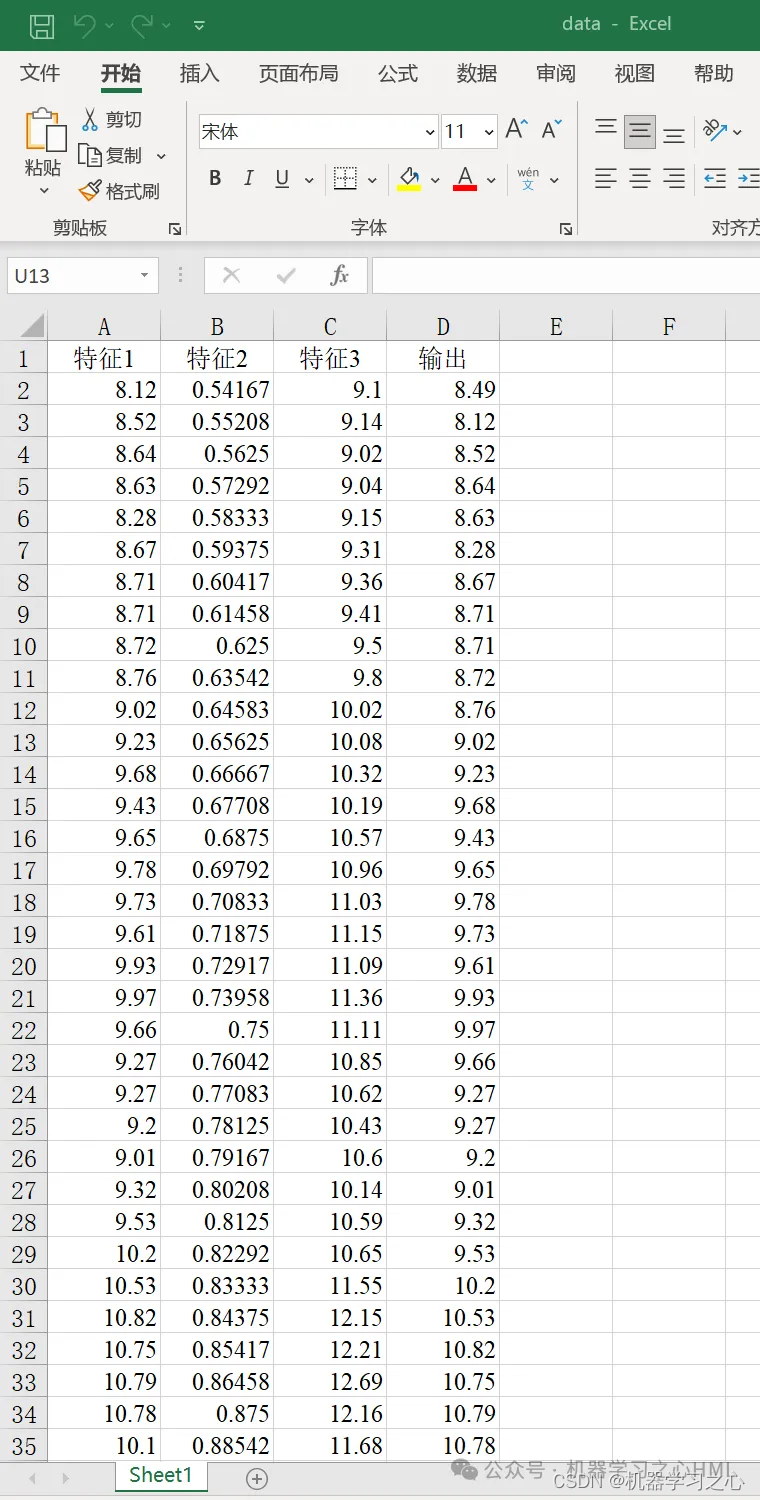
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化) 目录 机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)效果一览基本介绍程序设计参考资料 效果一览 基本介…...

idea导入项目根目录缺失解决方法
点击File→Project Structure 在弹出的界面选择Modules→→import Module,然后选择你导入文件点击OK, 选择导入类型next→勾选Search for projects recursively(递归寻找项目)→next→Finish最后选择根目录点击OK即可。...

VMware虚拟机下ubuntu配置
VMware虚拟机下ubuntu配置 1 Ubuntu换源2 安装VMware Tools2.1 一般安装2.2 代码安装 3 安装中文输入法参考 VMware虚拟机安装及虚拟机下安装ubuntu可参见另一博客-VMware虚拟机安装及虚拟机下安装ubuntu 1 Ubuntu换源 Ubuntu换源的主要用途是通过更换软件源来提高软件下载速…...

回调函数复习
#include <iostream>// 定义一个回调函数类型 typedef void (*CallbackFunction)(int);// 函数接受一个回调函数作为参数 void performOperation(int value, CallbackFunction callback) {// 执行某些操作std::cout << "Performing operation with value: &qu…...

开源AI智能名片O2O商城微信小程序在顾客价值链优化中的应用与探索
摘要:随着信息技术的飞速发展,顾客的消费行为模式正经历着前所未有的变革。在这一背景下,开源AI智能名片O2O商城微信小程序作为一种创新的营销与服务平台,正逐步成为企业连接顾客、优化顾客价值链的重要工具。本文旨在探讨开源AI智…...

idea-springboot后端所有@注释含义汇总-持续更新!
(1)启动类 ①SpringBootApplication 出现这个代表这个就是整个程序的入口,是运行的开始位置 ②ComponentScan("com.example.dao.impl") 启动时自动扫描制定beans包 (2)mapper层(Dao层…...

七:C语言-数组
七:C语言-数组 数组是一组相同类型元素的集合数组中存放的是1个或者多个数据,但是数组元素个数不能为0数组中存放的多个数据,类型是相同的数组分为一维数组和多维数组,多维数组一般比较多见的是二维数组存放在数组中的值被称为数…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
