基于FPGA的以太网设计(4)----详解PHY的使用(以YT8531为例)
目录
1、前言
2、如何了解PHY芯片?
2.1、总览
2.2、管脚
2.3、编码
2.4、自协商
2.5、环回模式
2.6、睡眠模式
2.7、复位
2.8、PHY地址
3、PHY芯片的寄存器配置
3.1、Basic Control Register (0x00)
3.2、Basic StatusRegister (0x01)
3.3、PHY Specific Status Register (0x11)
文章总目录点这里:《FPGA接口与协议》专栏的说明与导航
1、前言
在前面的文章,我们已经了解了FPGA实现千兆以太网的电路架构,即 MAC + PHY + 变压器 + RJ45,其示意图如下:
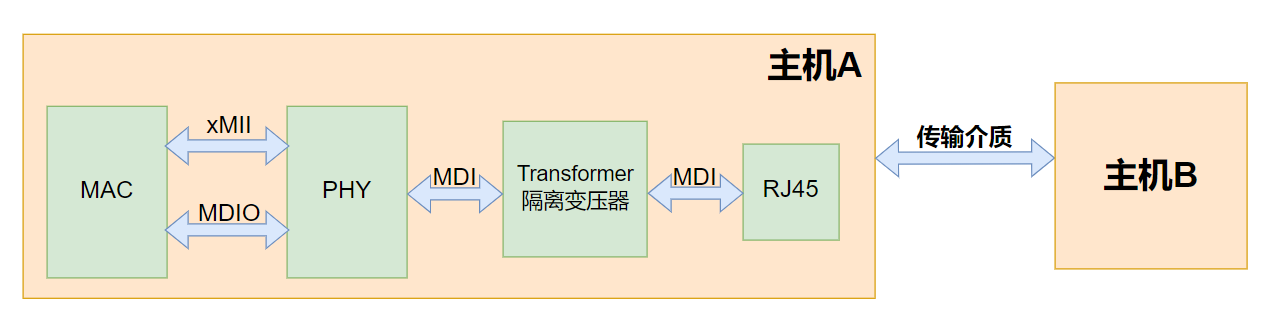
变压器和RJ45实现的都只是电气方面的功能,比较简单,我们并不需要对其进行设置,所以不需要做过多了解。MAC的实现则是重点,它需要用FPGA写代码来实现数据聊路层的功能,也就是说FGPA就是这个架构里的MAC(后面的文章会着重讲解如下实现这些功能)。
PHY呢?现在的千兆网主流方案基本都是使用独立的PHY(集成芯片),这意味着我们作为一个FPGAer,其实并不需要深入了解PHY的原理,只要了解PHY的对外接口,能正常地实现数据收发就行了。
相关文章:

基于FPGA的以太网设计(4)----详解PHY的使用(以YT8531为例)
目录 1、前言 2、如何了解PHY芯片? 2.1、总览 2.2、管脚 2.3、编码 2.4、自协商 2.5、环回模式 2.6、睡眠模式 2.7、复位 2.8、PHY地址 3、PHY芯片的寄存器配置 3.1、Basic Control Register (0x00) 3.2、Basic StatusRegister (0x01) 3.3、PHY Specific Status…...
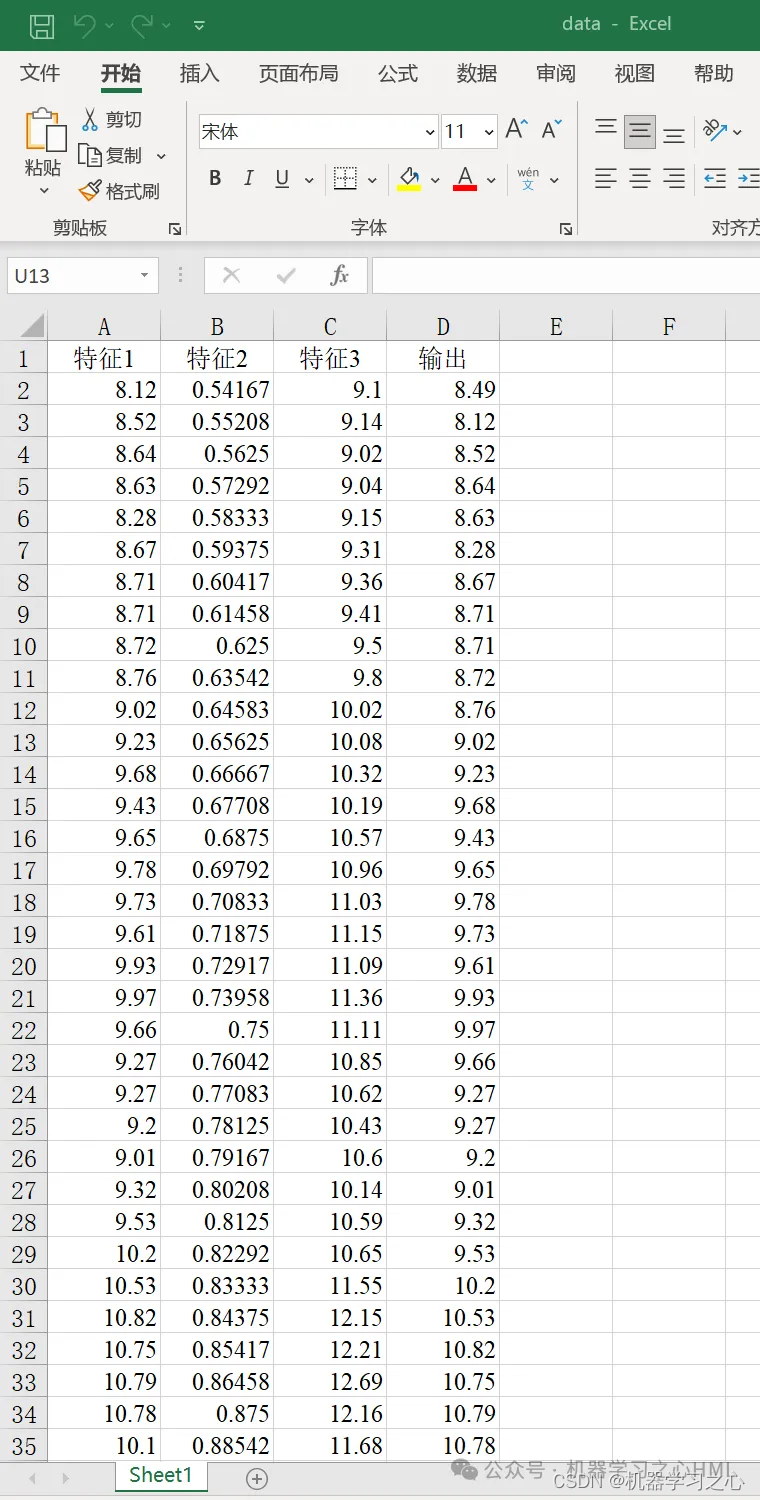
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化) 目录 机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)效果一览基本介绍程序设计参考资料 效果一览 基本介…...

idea导入项目根目录缺失解决方法
点击File→Project Structure 在弹出的界面选择Modules→→import Module,然后选择你导入文件点击OK, 选择导入类型next→勾选Search for projects recursively(递归寻找项目)→next→Finish最后选择根目录点击OK即可。...

VMware虚拟机下ubuntu配置
VMware虚拟机下ubuntu配置 1 Ubuntu换源2 安装VMware Tools2.1 一般安装2.2 代码安装 3 安装中文输入法参考 VMware虚拟机安装及虚拟机下安装ubuntu可参见另一博客-VMware虚拟机安装及虚拟机下安装ubuntu 1 Ubuntu换源 Ubuntu换源的主要用途是通过更换软件源来提高软件下载速…...

回调函数复习
#include <iostream>// 定义一个回调函数类型 typedef void (*CallbackFunction)(int);// 函数接受一个回调函数作为参数 void performOperation(int value, CallbackFunction callback) {// 执行某些操作std::cout << "Performing operation with value: &qu…...

开源AI智能名片O2O商城微信小程序在顾客价值链优化中的应用与探索
摘要:随着信息技术的飞速发展,顾客的消费行为模式正经历着前所未有的变革。在这一背景下,开源AI智能名片O2O商城微信小程序作为一种创新的营销与服务平台,正逐步成为企业连接顾客、优化顾客价值链的重要工具。本文旨在探讨开源AI智…...

idea-springboot后端所有@注释含义汇总-持续更新!
(1)启动类 ①SpringBootApplication 出现这个代表这个就是整个程序的入口,是运行的开始位置 ②ComponentScan("com.example.dao.impl") 启动时自动扫描制定beans包 (2)mapper层(Dao层…...

七:C语言-数组
七:C语言-数组 数组是一组相同类型元素的集合数组中存放的是1个或者多个数据,但是数组元素个数不能为0数组中存放的多个数据,类型是相同的数组分为一维数组和多维数组,多维数组一般比较多见的是二维数组存放在数组中的值被称为数…...

【numpy】浮点数比较大小
对于浮点数的比较,由于浮点数的精度问题,直接比较可能会遇到精度不一致的情况。为了比较浮点数的大小,可以使用一定的容差范围,避免因微小的误差导致的错误判断。使用 np.isclose() 或 np.allclose() 函数可以方便地进行这种比较。…...

ISC.AI 2024周鸿祎:发展安全大模型是安全迈向“自动驾驶”的必由之路
7月31日,ISC.AI 2024第十二届互联网安全大会在北京盛大开幕。360集团创始人周鸿祎就“打造安全大模型 引领安全行业革命”主题发表演讲。周鸿祎表示,发展安全大模型是安全迈向“自动驾驶”的必由之路,也是成功之路,而落地安全大模…...

并查集(未压缩未按秩合并)
并查集(Union-Find)是一种用于处理不相交集合(disjoint-set)的数据结构,主要用于处理连通性问题。并查集支持两种操作: 查找(Find):确定元素所属的集合。合并࿰…...

读书其实并没有那么大的作用
开场白 Hey,书虫们和生活探索者们!今天我们来聊聊一个老生常谈却又常谈常新的话题——读书。有人说,读书能改变命运,但也有人说,读书不过是生活的调味品。那么,读书到底有啥用?让我们一起来扒一…...

微信小程序/vue将金额/数字转为千分位显示在页面上
vue将金额转为数字显示在页面上 toThousands (number) {let isNegative_ false // 判断正负if (Number(number) < 0) {isNegative_ truenumber String(number).split(-)[1] // 分离负号 并把String类型的数字并赋值给number}if (Number(number) ! 0 && Math.abs…...

如何查看树莓派的 OS 和内核版本
在使用树莓派开发的时候,有时候需要知道树莓派的一些基本信息,如:OS 版本,内核版本,CPU 构架等,在使用 40 pin 扩展接口的时候,需要知道每个管脚的具体定义。 1. 查看 OS 版本: 使…...

php的mysql操作可实现简单登录功能
文章目录 1. 表单和请求(1) 表单操作(2) 网络请求(3) $_REQUEST超全局变量 2. mysql数据库操作1) mysqli连接操作2) 操作数据库3) 预处理语句4) pdo操作数据库5) 创建连接并执行查询语句 1. 表单和请求 主要使用到**$_GET** 和 $_POST这两个超全局变量,分别对应两种请求 (1) …...

c#复制窗体Form方法
直接复制三个类粘贴到vs的项目中...

C:图案打印
引言 本篇文章讲了一些常见的图形编程题,并总结了一些规律。 1、打印空心正方形 1.1 代码展示: #include<stdio.h> int main() {int a 0;//边长初始化scanf("%d", &a);//输入边长的值{int i 0;for (i 0; i < a; i)//控制行…...

WebLogic:弱口令,木马反弹连接
weblogic WebLogic 是 Oracle 公司开发的应用服务器,主要用作开发、集成、部署和管理大型分布式 Web 应用、网络应用和数据库应用的 Java 应用服务器。它在历史上曾出现过多个安全漏洞,其中包括弱口令、任意文件上传、SSRF、反序列化漏洞等 常见版本&a…...

深度学习图像处理环境搭建
Anaconda安装 Anaconda介绍 Anaconda是一个用于科学计算和数据科学的开源发行版,它包含了许多流行的Python库和工具,旨在简化数据分析和机器学习任务的开发过程。Anaconda提供了一个集成的开发环境,包括Python解释器、包管理工具࿰…...

这几个高级爬虫软件和插件真的强!
亮数据(Bright Data) 亮数据是一款强大的数据采集工具,以其全球代理IP网络和强大数据采集技术而闻名。它能够轻松采集各种网页数据,包括产品信息、价格、评论和社交媒体数据等。 网站:https://get.brightdata.com/we…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
