程序员面试题------N皇后问题算法实现
N皇后问题是一个著名的计算机科学问题,它要求在N×N的棋盘上放置N个皇后,使得它们之间不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。这个问题可以看作是一个回溯算法问题,通过逐步尝试不同的放置位置,并在发现不满足条件时回溯到上一步,来找到所有可能的解。
以下是解决N皇后问题的详细解题思路:
- 初始化棋盘:创建一个N×N的棋盘,通常使用一个二维数组来表示,初始化所有位置为空,即没有放置任何皇后。
- 选择位置:从棋盘的第一行开始,尝试在每一行中选择一个位置放置一个皇后。由于棋盘是N×N的,因此每一行都有N个可能的放置位置。
- 检查冲突:在选择了一个位置后,需要检查该位置是否与其他已经放置的皇后冲突。这包括检查同一列、两条对角线(一条是从左上到右下,另一条是从右上到左下)是否有冲突。如果有冲突,则说明当前放置位置不合适,需要回溯到上一步,选择另一个位置。
- 放置皇后:如果当前选择的位置没有冲突,则在该位置放置一个皇后,并标记该位置为已占用。
- 递归:在当前行放置了一个皇后后,需要继续在下一行中放置皇后。这需要重复执行选择位置、检查冲突和放置皇后的步骤,直到所有N个皇后都被放置在棋盘上。
- 回溯:如果在放置皇后的过程中发现当前选择的位置不合适(即有冲突),则需要回溯到上一步,并尝试在之前已经放置的皇后所在的行中选择一个新的位置。
- 收集解:当所有N个皇后都被放置在棋盘上且没有冲突时,得到了一个有效的解。将这个解收集起来,继续寻找下一个解。
- 结束条件:当所有可能的行都尝试过,仍然没有找到一个有效的解时,算法结束。
N皇后问题的一个关键点是回溯算法的使用。通过递归地尝试不同的放置位置,并在发现不合适时回溯,算法能够找到所有可能的解。这个过程需要仔细设计和实现,以确保能够正确地检查冲突和回溯。
N皇后问题有哪些经典算法实现?
N皇后问题有多种经典算法实现,其中最著名的是回溯算法。回溯算法通过递归地在棋盘上尝试放置皇后,并在发现冲突时回溯到上一步,以找到所有可能的解决方案。以下是几种实现N皇后问题的经典算法:
- 回溯算法:
- 回溯算法是解决N皇后问题的最直接和最常用的方法。它通过递归地在棋盘上尝试放置皇后,并在发现冲突时回溯到上一步。这种方法可以找到所有可能的解决方案。
- 位运算:
- 位运算是一种高效的方法,它使用位向量来表示棋盘上的皇后放置情况。通过位运算,可以快速判断是否有冲突,并且能够优化空间复杂度。
- 动态规划:
- 动态规划是一种将问题分解为更小子问题的方法。对于N皇后问题,可以使用动态规划来避免重复计算,从而提高算法的效率。
- 迭代算法:
- 迭代算法是一种使用循环结构而不是递归结构的算法。它通过模拟回溯过程来找到解决方案,但通常不如递归算法直观。
- 启发式算法:
- 启发式算法,如遗传算法、模拟退火等,可以在没有完全解决方案的情况下找到近似解。这些算法适用于N皇后问题的变体,如在限制条件下寻找最优解。
回溯算法是解决N皇后问题的最经典和最直接的方法,因此通常被视为标准实现。位运算和动态规划是提高算法效率的优化方法,而迭代算法和启发式算法适用于特定场景和变体。在面试或算法竞赛中,回溯算法是最常见的实现方式。
- 启发式算法,如遗传算法、模拟退火等,可以在没有完全解决方案的情况下找到近似解。这些算法适用于N皇后问题的变体,如在限制条件下寻找最优解。

来检查同一列是否有冲突,通过异或运算(XOR)来检查同一斜线上是否有冲突。
-
回溯:如果在放置皇后的过程中发现冲突,则需要回溯到上一步,并尝试在之前已经放置的皇后所在的行中选择一个新的位置。
-
收集解:当所有N个皇后都被放置在棋盘上且没有冲突时,得到了一个有效的解。将这个解收集起来,继续寻找下一个解。
位运算应用于N皇后问题的优点是能够快速判断冲突,并且只需要一个整数数组来表示整个棋盘的状态,从而优化了空间复杂度。这种方法通常比传统的回溯算法更加高效。
代码示例
以下是一个简单的 Python 代码示例,展示了如何使用回溯算法解决 N 皇后问题:
def solveNQueens(n):def is_safe(board, row, col):# Check this row on left sidefor i in range(col):if board[row][i] == 'Q':return False# Check upper diagonal on left sidefor i, j in zip(range(row, -1, -1), range(col, -1, -1)):if board[i][j] == 'Q':return False# Check lower diagonal on left sidefor i, j in zip(range(row, n, 1), range(col, -1, -1)):if board[i][j] == 'Q':return Falsereturn Truedef solve(board, col):if col >= n:return Truefor i in range(n):if is_safe(board, i, col):board[i][col] = 'Q'if solve(board, col + 1):return Trueboard[i][col] = '.' # Backtrackreturn Falseboard = [['.' for _ in range(n)] for _ in range(n)]if not solve(board, 0):return "Solution does not exist"return board
# Example usage:
n = 4
print(solveNQueens(n))
这个代码定义了一个 solveNQueens 函数,它接受一个整数 n 作为参数,表示棋盘的大小。它内部定义了一个辅助函数 is_safe 来检查是否可以在棋盘的某一位置放置一个皇后,以及一个递归函数 solve 来尝试在棋盘上放置所有皇后。最终,solveNQueens 函数返回所有可能的解决方案。
请注意,这段代码是一个简化的示例,它没有处理所有可能的边界条件和优化。在实际的面试中,面试官可能会要求你实现一个更完整和优化的版本。

相关文章:

程序员面试题------N皇后问题算法实现
N皇后问题是一个著名的计算机科学问题,它要求在NN的棋盘上放置N个皇后,使得它们之间不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。这个问题可以看作是一个回溯算法问题,通过逐步尝试不同的放置位置…...
【C++学习】6、继承
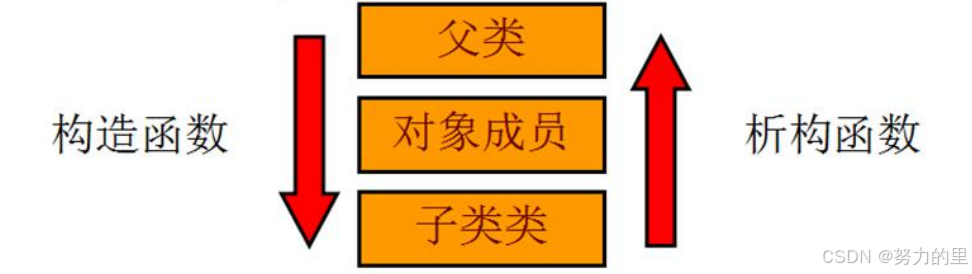
1、什么是继承? 继承描述的是类与类之间的关系,A类继承B类,A类就拥有B类的数据和方法。 继承的方式: 公有继承(public) 保护继承(protected) 私有继承(private&…...
 按键与外部中断)
从零开始的MicroPython(三) 按键与外部中断
上一篇:从零开始的MicroPython(二) GPIO及点灯代码 文章目录 前言硬件原理软件原理注意代码编写轮询外部中断其他 前言 点灯是嵌入式GPIO输出的典型,按键则是输入的典型。 硬件原理 按键对角接通。 软件原理 如果是一端接高电平,一端接单…...

Windows下编译安装Kratos
Kratos是一款开源跨平台的多物理场有限元框架。本文记录在Windows下编译Kratos的流程。 Ref. from Kratos KRATOS Multiphysics ("Kratos") is a framework for building parallel, multi-disciplinary simulation software, aiming at modularity, extensibility, a…...
)
汽车-腾讯2023笔试(codefun2000)
题目链接 汽车-腾讯2023笔试(codefun2000) 题目内容 现在塔子哥有 n 个汽车,所有的汽车都在数轴上,每个汽车有1.位置 pos 2.速度 v ,它们都以在数轴上以向右为正方向作匀速直线运动。 塔子哥可以进行任意次以下操作:选择两个汽车…...

软测面试二十问(最新面试)
1.软件测试的流程是什么 参加需求评审会,解决需求疑问---写测试用例---对测试用例进行评审---评审后开始执行测试---提交bug---追踪bug---关闭bug---回归测试---交叉测试---编写测试报告---冒烟测试 2.什么是黑盒测试和白盒测试?它们有何区别 黑盒测试…...

风吸杀虫灯采用新型技术 无公害诱虫捕虫
TH-FD2S】风吸杀虫灯利用害虫的趋光性和对特定波长的光源(如紫外光、蓝光)的敏感性,通过光波引诱害虫成虫扑灯。同时,内置的风扇产生强烈的气流,形成负压区,将害虫迅速吸入到收集器中。害虫在收集器内被风干…...
)
随手记录第十二话 -- JDK8-21版本的新增特性记录(Lambda,var,switch,instanceof,record,virtual虚拟线程等)
本文主要用于记录jdk8以来的新增特性及使用方法! 1.Java8 Lambda表达式(8) 1.1 方法引用 List<String> list List.of("1", "2", "3");list.forEach(i -> System.out.println(i));//方法引用list.forEach(System.out::println);1.2 接…...
SpringCloud网关 SpringBoot服务 HTTP/HTTPS路由/监听双支持
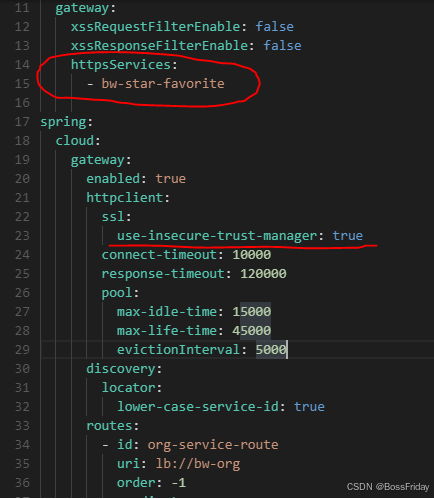
背景 一般来说SpringCloud Gateway到后面服务的路由属于内网交互,因此路由方式是否是Https就显得不是那么重要了。事实上也确实如此,大多数的应用开发时基本都是直接Http就过去了,不会一开始就是直接上Https。然而随着时间的推移,…...

JavaScript做网页是否过期的处理
通过路由上的参数生成唯一md5和路由上token做验证_md5 token-CSDN博客 前言:基于这篇文章我们做网页是否超时,网页是否过期的处理。打开一个网页允许他在一定时间内可以访问,过了这个时间就不可以访问了,encrypt是h5加密方法&…...

python coding时遇到的问题
Q:只有cpu的时候加载模型 A:checkpoint torch.load(model_path, map_locationtorch.device(‘cpu’)) Q:vscode的文件路径和spyder的不一样 A:在vscode中,右键要用的文件,选择“文件相对路径”...

攻防演练号角吹响,聚铭铭察高级威胁检测系统助您零失分打赢重保攻坚战
在数字化浪潮中,攻防演练成为了衡量网络安全防御力的核心标尺,其重要性与日俱增。这项由政府、行业监管或企业内部主导的安全活动,随着互联网普及而兴起,现已发展成为全球公认的检验网络安全体系效能的标准。它不仅关乎技术实力的…...

个人量化交易兴起!有什么好用的量化软件推荐?迅投QMT量化平台简介!
QMT是专门为机构、活跃投资者、高净值客户等专业投资者研发的智能量化交易终端,拥有高速行情、极速交易、策略交易、多维度风控等专业功能,满足专业投资者的特殊交易需求。覆盖业务范围广:沪深A股、港股通、两融、期权、期货。 适合用QMT的投资者&#x…...

SQL labs-SQL注入(七,sqlmap对于post传参方式的注入,2)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。参考:SQL注入之Header注入_sqlmap header注入-CSDN博客 序言: 本文主要讲解基于SQL labs靶场,sqlmap工具进行的post传参方式的SQL注入,…...

SAM 2: Segment Anything in Images and Videos
Introduction 提出的目的: 1.现有的应用像自动驾驶,AR等来说都是需要temporal localization beyond image-level segmentation(时序定位而不仅是图片分割) 2. 一个好的分割模型不应该仅仅局限于图片领域,而是图视频两…...

软件测试面试,如何自我介绍?
又是一年金九银十,相信不少小伙伴都在准备跳槽面试,而面试中一个必不可少的环节就是自我介绍,所以,今天我们就来聊一聊软件测试面试中如何自我介绍。 为什么要自我介绍 在讨论如何自我介绍之前,我们先来讨论一下为…...

力扣第四十七题——全排列II
内容介绍 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2: 输入:nums [1,2,3] 输出:[[1,2,3],…...

Springer旗下中科院2区TOP,国人优势大!
关注GZH【欧亚科睿学术】,第一时间了解期刊最新动态! 1 通信网络类 【期刊简介】IF:4.0-5.0,JCR1区,中科院3区 【出版社】ELSEVIER出版社 【检索情况】SCIE&EI双检,CCF-C类 【征稿领域】通信网络的…...

【C++】C++入门知识详解(下)
大家好~我们接着【C】C入门知识详解(上)-CSDN博客来介绍另一些C入门基础知识。 1.缺省值和缺省参数 缺省参数就是声明或定义函数时为函数的参数指定一个缺省参数。在调用该函数时,如果没有指定实参,则采用该形参的缺省值…...
分压电阻方式的ADC电压校准
无人机有个流程是电池电压校准。具体做法是:让你用万用表测量一下电池两端的电压,然后输入到文本框中,电机计算能重新计算出电压分压器的值,从而获得电池电压值。 这种方法实现的原理是这样的: 电阻分压检测电压原理,以上图为例: 当电路确定时,R2/(R1+R2)是一个定值R,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
