钉耙编程(3)
1001深度自同构
Problem Description
对于无向图中的点,定义一个点的度为与其相连的边的条数。
对于一棵有根树,定义一个点的深度为该点到根的距离。
对于由若干有根树构成的森林,定义该森林是深度自同构的,当且仅当森林中任意两个深度相同的节点都有相同的度。
请计数有多少个深度自同构的无编号有根树森林,使得其恰好由 nn 个节点构成,答案对 998244353998244353 取模。
Input
一个整数 N (1≤N≤106)N (1≤N≤106),代表计数的范围。
Output
输出一行 NN 个整数,第 ii 个数代表 n=in=i 时的答案,对 998244353998244353 取模。

标准代码:
#include<bits/stdc++.h>
using namespace std;
#define N 1000007
#define mod 998244353
int f[N] = {0, 1}, ans[N];
int main() {cin.tie(0);ios::sync_with_stdio(false);int n; cin >> n;
// 也可以这样写
// for (int i = 1; i <= n; ++i)
// for (int j = i; j <= n; j += i) (f[j+1]+=f[i])%=mod;for (int i = 1; i <= n; i++)for (int j = 1; i * j <= n; j++) (f[j * i + 1] += f[i]) %= mod;for (int i = 1; i <= n; ++i) for (int j = i; j <= n; j += i) (ans[j] += f[i]) %= mod;for (int i = 1; i <= n; ++i) printf("%d ", ans[i]);return 0;
}1007 单峰数列
Problem Description
对于一个整数数列,如果其先严格递增,然后在某一点后严格递减,我们称这个数列为单峰数列(严格递增和严格递减的部分均要是非空)。
给定长度为 𝑛n 的整数数列 𝑎1,𝑎2,…,𝑎𝑛a1,a2,…,an ,请你支持 𝑞q 次操作:
-
1 l r x:将 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟al,al+1,…,ar 的每个数加 𝑥x。 -
2 l r:判断 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟al,al+1,…,ar 的元素是否全都相同。 -
3 l r:判断 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟al,al+1,…,ar 是否严格升序排序。当 𝑙=𝑟l=r 时,认为符合严格升序排序。 -
4 l r:判断 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟al,al+1,…,ar 是否严格降序排序。当 𝑙=𝑟l=r 时,认为符合严格降序排序。 -
5 l r:判断 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟al,al+1,…,ar 是否为单峰数列。保证 𝑟−𝑙+1≥3r−l+1≥3。
Input
第一行输入包含一个整数 𝑛 (3≤𝑛≤105)n (3≤n≤105)。
第二行输入包含 𝑛n 个整数 𝑎1,𝑎2,…,𝑎𝑛 (0≤𝑎𝑖≤109)a1,a2,…,an (0≤ai≤109)。
第三行输入包含一个整数 𝑞 (1≤𝑞≤2×105)q (1≤q≤2×105)。
接下来的 𝑞q 行,每行描述一个操作,格式见题目描述。对于第一类操作,保证 −109≤𝑥≤109−109≤x≤109。
Output
对于每个询问输出一行一个整数,如果查询符合要求输出 1,否则输出 0。


解析:

代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef array<int, 4> state;
const int MAXN = 200000+5;
ll a[MAXN], b[MAXN];
state tr[MAXN<<2]; //线段树开4倍
int n, q;
state unite(state a, state b){state tmp;tmp[0] = a[0] & b[0];tmp[1] = a[1] & b[1];tmp[2] = a[2] & b[2];tmp[3] = (a[1] & b[2]) | (a[1] & b[3]) | (a[3] & b[2]);return tmp;
}
void up(int x){tr[x] = unite(tr[x<<1], tr[x<<1|1]);
}
void build(int p,int l,int r){if(l==r){if (b[l] == 0) tr[p][0] = 1;else if (b[l] > 0) tr[p][1] = 1;else tr[p][2] = 1;return;}int mid=r+l>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);up(p);
}
void update(int p,int l,int r,int x,int v){if(l==r&l==x){b[l]+=v;if (b[l] == 0) tr[p][0] = 1;else if (b[l] > 0) tr[p][1] = 1;else tr[p][2] = 1;return;}int mid=l+r>>1;if(x<=mid) update(p<<1,l,mid,x,v);else update(p<<1|1,mid+1,r,x,v);up(p);
}
state query(int p,int l,int r,int L,int R){ //现在:l,r 要查:L,R;if(l>=L&&r<=R){return {tr[p][0], tr[p][1], tr[p][2], tr[p][3]};}int mid=l+r>>1;if(R<=mid) return query(p<<1,l,mid,L,R);else if(L>mid) return query(p<<1|1,mid+1,r,L,R);else{state left=query(p<<1,l,mid,L,R);state rigth=query(p<<1,l,mid,L,R);return unite(left,rigth);}
}
int main(){cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];b[i] = a[i] - a[i-1];}build(1, 2, n);cin >> q;while(q--){int op, l, r, x;cin >> op >> l >> r;if(op == 1){cin >> x;if(l > 1) update(1, 2, n, l, x);if(r < n) update(1, 2, n, r+1, -x);} else if(op == 2){if(l == r){cout << "1\n";continue;}cout <<query(1,2,n,l+1,r)[0]<<endl;}else if(op==3){if(l == r){cout << "1\n";continue;}cout <<query(1,2,n,l+1,r)[1]<<endl;}else if(op==4){if(l == r){cout << "1\n";continue;}cout <<query(1,2,n,l+1,r)[2]<<endl;}else{cout <<query(1,2,n,l+1,r)[3]<<endl;}}return 0;
}1008比特跳跃
Problem Description
比特国由 nn 个城市组成,编号为 1,2,⋯,n1,2,⋯,n。
有 mm 条双向道路连接这些城市,第 ii 条连通城市 uiui 和城市 vivi,通过这条道路需要花费 titi 的时间。
此外,比特国的人们还可以使用“比特跳跃“来通行于任意两个城市之间。
从城市 xx 通过比特跳跃移动到城市 yy 需要花费 k×(x∣y)k×(x∣y) 的时间,其中 ∣∣ 表示按位或。比特跳跃可以使用任意多次。
现在请你计算出,从 11 号城市移动到每个城市所需的最短时间。
Input
第一行一个整数 t (1≤t≤15)t (1≤t≤15),代表数据组数。
对于每组数据:
第一行三个整数 n,m,k (2≤n≤105,0≤m≤105,0≤k≤106)n,m,k (2≤n≤105,0≤m≤105,0≤k≤106),代表城市个数,道路条数,比特跳跃的系数。
接下来 mm 行,每行三个整数 ui,vi,ti (1≤ui,vi≤n,0≤ti≤109)ui,vi,ti (1≤ui,vi≤n,0≤ti≤109) ,代表一条道路的信息。
保证所有测试数据的 ∑n≤106,∑m≤106∑n≤106,∑m≤106 。
Output
对于每组数据,输出一行 n−1n−1 个整数,代表从 11 号城市移动到编号为 2,3,…,n2,3,…,n 的城市所需的最短时间。

解析:

代码:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e5+5;
struct point{int id,val; //起始点到该点当前的距离 bool operator <(const point &n1)const{return val>n1.val; //从小到大 }
};
priority_queue<point>q;
int h[N],v[2*N],ne[2*N],w[2*N];
int vist[N],ans[N]; //是否收录进最优路线,起始点到该点当前的距离;
int idx; //从1开始
int mind[N];
void add(int a,int b,int c){ne[++idx]=h[a]; h[a]=idx; v[idx]=b; w[idx]=c;
}
int lowbit(int i){return i&(-i);
}
int main(){
// freopen("D:\\1008(4).txt","w",stdout);int t; cin>>t;while(t--){memset(ans,0x3f,sizeof(ans));memset(vist,0,sizeof(vist));int n,m,k; scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=m;i++){int a,b,c; scanf("%d%d%d",&a,&b,&c); add(a,b,c);add(b,a,c);}for(int j=2;j<=n;++j) add(1,j,1ll*k*(1|j));q.push({1,0});while(q.size()){point tp=q.top(); q.pop();if(vist[tp.id]) continue;vist[tp.id]=1;ans[tp.id]=tp.val;for(int i=h[tp.id];i;i=ne[i])if(ans[tp.id]+w[i]<ans[v[i]]){ans[v[i]]=ans[tp.id]+w[i];q.push({v[i],ans[v[i]]});}}printf("%d ",ans[2]);for(int i=3;i<=n;i++)printf("%d ",ans[i]);printf("\n");for(int i=1;i<=n;i++) mind[i]=ans[i];for(int i=2;i<=n;i++){if(i==lowbit(i)) continue;for(int j=1;j<=n;j<<=1)if (i&j) mind[i]=min(mind[i],mind[i^j]);if(mind[i]+1ll*k*i<ans[i]) ans[i]=mind[i]+1ll*k*i;}for (int i=1;i<=n;++i) vist[i]=0, q.push({i,ans[i]});while(q.size()){point tp=q.top(); q.pop();if(vist[tp.id]) continue;vist[tp.id]=1;ans[tp.id]=tp.val;for(int i=h[tp.id];i;i=ne[i])if(ans[tp.id]+w[i]<ans[v[i]]){ans[v[i]]=ans[tp.id]+w[i];q.push({v[i],ans[v[i]]});}}printf("%d ",ans[2]);for(int i=3;i<=n;i++)printf("%d ",ans[i]);printf("\n");}
}1011 抓拍
Problem Description
学校里有 𝑛n 名同学,初始时第 𝑖i 位同学从 (𝑥𝑖,𝑦𝑖)(xi,yi) 出发,以每秒 11 米的速度散步。
同学们散步的方向有东南西北四种可能。假设有一位同学正在位于 (0,0)(0,0),则下一秒︰
- 如果向东走,到达 (1,0)(1,0)
- 如果向西走,到达 (−1,0)(−1,0)
- 如果向南走,到达 (0,−1)(0,−1)
- 如果向北走,到达 (0,1)(0,1)
假设散步过程会进行无限长的时间,同学们散步的方向不会改变,并且忽略碰撞的情况(允许某个时刻多人在同一个点,互不影响)。
现在你可以选择某个非负整数秒时刻抓拍照片。
一张照片可以用长方形 ((𝑒,𝑛),(𝑤,𝑠))((e,n),(w,s)) 表示,东北角为 (𝑒,𝑛)(e,n),西南角为 (𝑤,𝑠)(w,s)。
只有抓拍的照片包含了所有同学时,我们才称这张照片是完美的。
请选择某个时刻抓拍一张完美的照片,使得照片的周长最小。
Input
第一行一个整数 𝑛 (1≤𝑛≤2×105)n (1≤n≤2×105),代表人数。
接下来 𝑛n 行,第 𝑖i 行包含两个整数 𝑥𝑖,𝑦𝑖 (−109≤𝑥𝑖,𝑦𝑖≤109)xi,yi (−109≤xi,yi≤109) 和一个字符 𝑑𝑖di ,由空格分隔,描述第 𝑖i 位同学。
𝑑𝑖di 是 'E', 'W', 'S', 'N' 之一,分别代表第 𝑖i 位同学散步的方向是东、西、南、北。
Output
输出一行一个整数,代表最短的完美照片的周长。

解析:
三分法:时间复杂度是log(1.5)^(n);求单峰函数的最值。
当n=1e9时log(1.5)^(n)=50;log(2)^(n)=30;
核心代码:

代码:
#include<iostream>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int x[N],y[N],fid[N];
int fx[4]={1,-1,0,0};
int fy[4]={0,0,-1,1};
int n;
ll check(ll t){ll mxx,mxy,mnx,mny;mxx=mxy=-0x3f3f3f,mnx=mny=0x3f3f3f;for(int i=1;i<=n;i++){ll tpx=x[i]+t*fx[fid[i]],tpy=y[i]+t*fy[fid[i]];mxx=max(mxx,tpx);mxy=max(mxy,tpy);mnx=min(mnx,tpx);mny=min(mny,tpy);}return (mxx-mnx)+(mxy-mny);
}
int main(){cin>>n;for(int i=1;i<=n;i++){char op;scanf("%d%d %c",&x[i],&y[i],&op);if(op=='E') fid[i]=0;else if(op=='W') fid[i]=1;else if(op=='S') fid[i]=2;else fid[i]=3;}ll l=0,r=2e9;ll tpl,tpr;while(l<=r){tpl=l+(r-l)/3,tpr=r-(r-l)/3;if(check(tpl)<=check(tpr)) r=tpr-1;else l=tpl+1;} printf("%lld",2*check(l));return 0;
}相关文章:

钉耙编程(3)
1001深度自同构 Problem Description 对于无向图中的点,定义一个点的度为与其相连的边的条数。 对于一棵有根树,定义一个点的深度为该点到根的距离。 对于由若干有根树构成的森林,定义该森林是深度自同构的,当且仅当森林中任意…...

python 线程池处理文件
使用多线程来加速文件复制的过程,可以使用Python的concurrent.futures模块中的ThreadPoolExecutor。代码如下: import glob import os import shutil from concurrent.futures import ThreadPoolExecutordef copy_image(image):imagepath image.replace…...

AI技术和大模型对人才市场的影响
012024 AI技术和大模型 2024年AI技术和大模型呈现出多元化和深入融合的趋势,以下是一些关键的技术方向和特点: 1. 生成式AI 生成式AI(Generative AI)在2024年继续快速发展,它能够创造全新的内容,而不仅仅…...

解释“location”和“position”
Explanation of “Location” and “Position” Location and position are terms often used interchangeably in everyday language, but they can have distinct meanings depending on the context. Below, we explore their definitions, differences, and examples of u…...

Netty 必知必会(三)—— ByteBuf
Netty ByteBuf工作原理,和NIO里ByteBuffer区别? Java NIO 提供了ByteBuffer 作为它 的字节容器,但是这个类使⽤起来过于复杂,⽽且也有些繁琐。 ByteBuf是Netty框架中的一个关键类,专门设计来处理字节数据,…...

芋道以开源之名行下作之事 恬不知耻 标榜自己开源 公开源码+sql 不用再加入知识星球
资源 链接: https://pan.baidu.com/s/1TeuxbAUfLQ5_BqMBF1kniQ?pwdcqud 提 取码: cqud 依次为后端、补充版的sql、前端 此文档内安装部署等一应俱全...

wordpress中,wp_posts 文章的状态 有哪些,分别对应什么数值
在WordPress中,wp_posts 表存储了网站上的所有内容,包括文章(posts)、页面(pages)、自定义文章类型(custom post types)等。这个表有一个名为 post_status 的字段,用于标…...

输入成绩问题(c语言)
1.问题:期中考试开始了,大家想要取得好成绩,争夺前五名,从键盘输入n个学生成绩(不超过40个),输出每组的前五名的成绩 两行,第一行输入一个整数,表示n个学生(…...

基于域名+基于ip+基于端口的虚拟主机+上线商务系统
一、回顾 1.jdk环境 tomcat服务器需要jdk环境 版本对应 tomcat9>jdk1.8 配置系统变量JAVA_HOME sed -i $aexport JAVA_HOME/usr/local/jdk22/ /etc/profile sed -i $aexport PATH$JAVA_HOME/bin:$PATH /etc/profile source /etc/profile java -version java…...

vue每次路由跳转前将页面滚动到顶部
在Vue.js应用中,特别是使用Vue Router进行页面路由管理时,router.beforeEach是一个非常有用的导航守卫(Navigation Guard)。它允许你在路由跳转之前执行一些逻辑,比如权限验证、页面跳转前的数据加载、滚动位置重置等。…...

【Qt】QDateTimeEdit
在Qt中,QDateEdit是用于选择日期的微调框,QTimeEdit是用于选择小时和分钟的微调框 QDateTimeEdit则是基于QDateEdit和QTimeEdit的组合控件,能够同时显示日期和时间,并允许用户以交互方式编辑日期 常用属性 属性说明dateTime时间…...

Redis和Mysql如何保持数据一致性
一般情况下,Redis是用来实现应用和数据库之间读操作得缓存层,主要目的是减少数据库IO,还可以提升数据的IO性能。 当应用程序需要去读取某个数据时,会首先尝试去Redis里面加载,如果命中就直接返回,如果没有…...

Java中Optional相关
Java中Optional相关 orElse 提供默认值以确保不会返回 null。 适用于默认情况下的备选值或简单计算结果。 // 如果 optionalName 为空,返回 "Unknown" Optional<String> optionalName Optional.empty(); String result optionalName.orElse(&q…...

AI在HR候选人关系管理中的革新应用
一、引言 随着人工智能(AI)技术的快速发展,其在人力资源管理(HR)领域的应用也日益广泛。特别是在候选人关系管理方面,AI技术不仅提高了管理效率,还使得候选人体验得到了极大的改善。本文将深入分…...
)
HTML+CSS+JavaScript制作七夕表白网页(含音乐+自定义文字+烟花特效)
利用HTMLCSSJavaScript制作了一个简单的七夕表白网页: 这是一个简单的表白功能,可以用于小哥哥小姐姐在情人节向心爱的人表白使用点击信封中间的爱心,会出现一封信由信封向外展开,与此同时会有烟花绽放,并且自动播放背…...
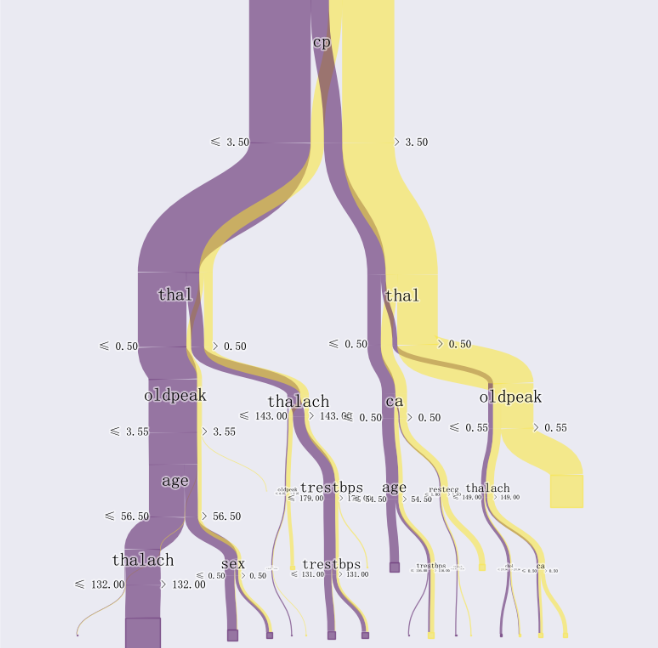
【Python机器学习系列】一文教你实现决策树模型可视化(案例+源码)
这是我的第335篇原创文章。 一、引言 决策树是一个有监督分类模型,本质是选择一个最大信息增益的特征值进行输的分割,直到达到结束条件或叶子节点纯度达到阈值。根据分割指标和分割方法,可分为:ID3、C4.5、CART算法。每一种颜色代…...
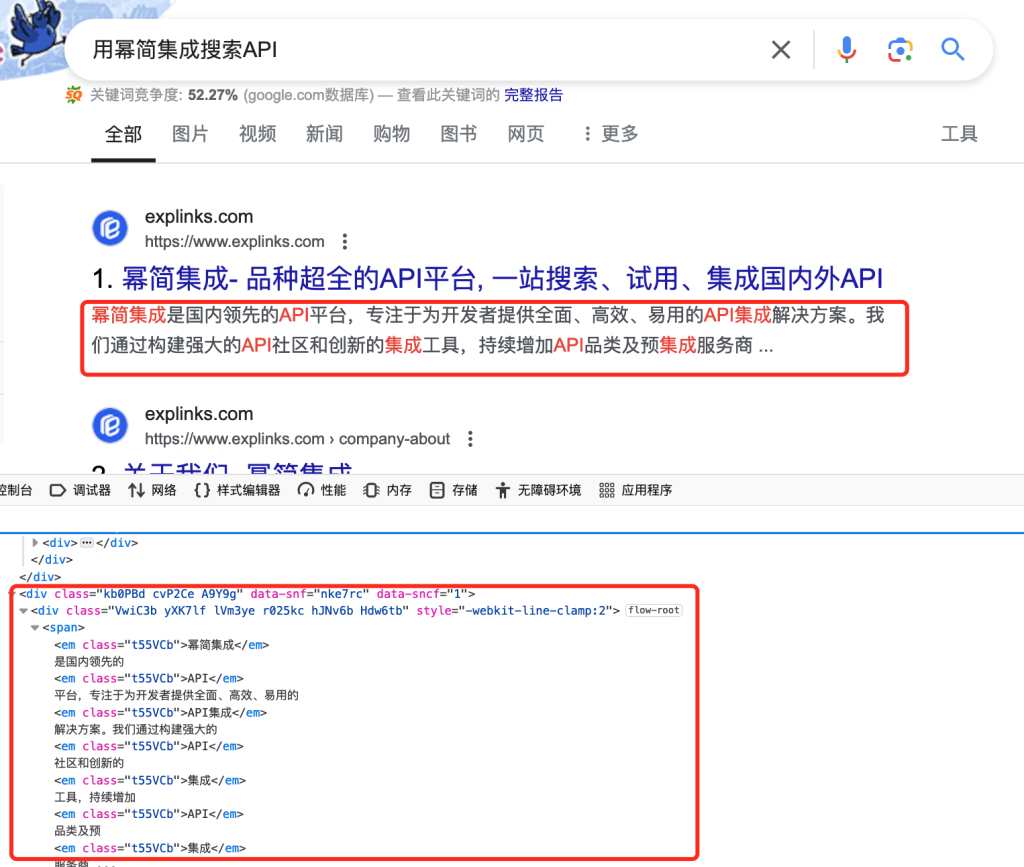
如何在Python中使用网页抓取API获得Google搜索结果
SERP是搜索引擎结果页的缩写,它是你在百度、谷歌、Bing等搜索引擎中提交查询后所得到的页面。搜索引擎需要给所有页面做排序,把最能解决我们需求的页面展示给我们,企业会非常关注结果页的排序,也就是本企业内容的自然排名情况。手…...

Postman高频面试题及答案汇总(接口测试必备)
Postman在软件测试的面试中,可以说是必考题了,既然是高频考题,当然得为粉丝宝宝们整理一波题库喽~ 一、Postman在工作中使用流程是什么样的? 二、你使用过Postman的哪些功能? 三、Postman如何管理测试环境ÿ…...

JavaEE 初阶(13)——多线程11之“定时器”
目录 一. 什么是“定时器” 二. 标准库的定时器 三. 定时器的实现 MyTimer 3.1 分析思路 1. 创建执行任务的类。 2. 管理任务 3. 执行任务 3.2 线程安全问题 四. 拓展 一. 什么是“定时器” 定时器是软件开发中的一个重要组件,类似于一个“闹钟”࿰…...

2024最新全开源付费进群系统源码二开修复版 支持易支付
内容目录 一、详细介绍二、效果展示1.部分代码2.效果图展示 三、学习资料下载 一、详细介绍 全开源付费进群系统源码,开源无加密无授权,优化电脑端访问布局,支持dai理,对接易支付通道,dai理可以配置自己易支付接口&am…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
