动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
class Solution {public int fib(int n) {if(n < 2) return n;int[] dp = new int[n + 1];dp[0] = 0; dp[1] = 1;for(int i = 2; i < dp.length; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
class Solution {public int climbStairs(int n) {if(n <= 1) return n;//初始化dp数组int[] dp = new int[n];dp[0] = 1;dp[1] = 2;//递推公式for(int i = 2; i < dp.length; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n-1];}
}746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length + 1];dp[0] = 0;dp[1] = 0;for(int i = 2; i < dp.length; i++){dp[i] = Math.min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[dp.length - 1];}
}相关文章:

动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 …...

CSS实现图片边框酷炫效果
一、前言 我们在浏览一些网页时,经常会看到一些好看酷炫的元素边框效果(如下图),那么这些效果是怎么实现的呢?我们知道,一般的边框,要么是实线,要么是虚线(点状…...

遇到 MySQL 死锁问题如何解决?
终于来到死锁检查线程的第三步,可以解决死锁了。 作者:操盛春,爱可生技术专家,公众号『一树一溪』作者,专注于研究 MySQL 和 OceanBase 源码。 爱可生开源社区出品,原创内容未经授权不得随意使用࿰…...

Pyinstaller打包OSError: could not get source code【终极解决】
pyinstaller 打包的时候,发现只要是torch.jit.script装饰的函数,会报以下错误: Traceback (most recent call last):File "torch/_sources.py", line 25, in get_source_lines_and_fileFile "inspect.py", line 1123, i…...
【计算机毕业设计】707高校宿舍管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

从C++看C#托管内存与非托管内存
进程的内存 一个exe文件,在没有运行时,其磁盘存储空间格式为函数代码段全局变量段。加载为内存后,其进程内存模式增加为函数代码段全局变量段函数调用栈堆区。我们重点讨论堆区。 托管堆与非托管堆 C# int a10这种代码申请的内存空间位于函…...

Linux进程间通信--IPC之无名管道
进程间通信(IPC,InterProcess Communication)是指在不同进程之间传播或交换信息。 IPC的方式通常有管道(包括无名管道和命名管道)、消息队列、信号量、共享存储、Socket、Streams支持不同主机上的两个进程的IPC。...

Oracle19c数据库system密码锁定
一、在oracle 19c数据库中,cdb中system用户被锁定,locked 二、所在的pdb中的system用户状态是正常的,但不可用,连接的时候提示账号已锁定 三、解决 在cdb中将system用户解锁。 alter user system account unlock;...
 方法和 equals(Object obj) 方法之间的关系)
java之hashCode() 方法和 equals(Object obj) 方法之间的关系
1、 hashCode() 方法和 equals(Object obj) 在Java中,hashCode() 方法和 equals(Object obj) 方法之间的关系是紧密相连的,特别是在使用基于哈希的集合(如 HashSet、HashMap、HashTable 等)时。这两个方法共同决定了对象在哈希表…...

首届「中国可观测日」圆满落幕
首届中国可观测日(Observability Day)在上海圆满落幕,为监控观测领域带来了一场技术盛宴。作为技术交流的重要平台,此次活动不仅促进了观测云与亚马逊云科技之间的深化合作,更标志着双方共同推动行业发展的重要里程碑。…...

[Docker][Docker NetWork][下]详细讲解
目录 1.网络管理命令1.docker network creatre2.docker network inspect3.docker network connect4.docker network disconnect5.docker network prune6.docker network rm7.docker network ls 2.docker bridge 详解0.基本概念1.默认 bridge2.自定义 bridge3.DNS解析4.端口暴露…...

安卓系统在未来如何更好地解决隐私保护与数据安全的问题?
安卓系统可以通过以下方式更好地解决隐私保护与数据安全的问题: 强化权限控制:安卓系统可以进一步加强对应用程序权限的管理,确保用户能够清楚地知道应用程序需要哪些权限,并给予用户更多的控制权,例如允许用户选择性地…...

MySQL innodb单表上限一般多少
参考:https://www.zhihu.com/question/351797203/answer/3137174084 1.MySQL innodb单表上限为啥都说是2k万条 2.GaussDB for MySQL 为啥可以突破单表2k万的限制 要讨论这两个问题,得先明确性下实际的DB部署环境 表是索引数据是放在磁盘上的…...
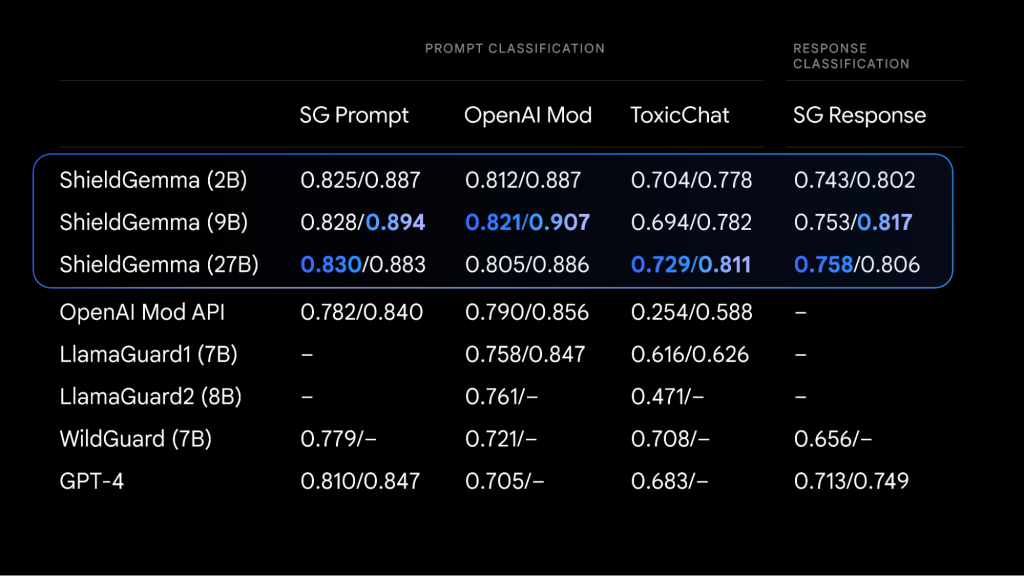
更小、更安全、更透明:Google发布的Gemma推动负责任AI的进步
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

基于Django框架的医疗耗材管理系统的设计实现-计算机毕设定制-附项目源码(可白嫖)48999
摘 要 在目前的形势下,科技力量已成为我国的主要竞争力。而在科学技术领域,计算机的使用逐渐达到成熟,无论是从国家到企业再到家庭,计算机都发挥着其不可替代的作用,可以说计算机的可用领域遍及生活、工作的各个方面。…...
:modbus tcp和modbusRTU的区别是什么?)
物联网协议篇(1):modbus tcp和modbusRTU的区别是什么?
Modbus TCP和Modbus RTU是Modbus协议中的两种主要变体,它们在多个方面存在显著的区别。以下是它们之间的主要区别: 1. 物理层和数据传输方式 Modbus TCP (TCP/IP): 使用以太网作为物理层,通过TCP/IP协议进行通信。数据以数据包的形式在TCP连接上传输,具有较高的通信速度和…...

JVM系列 | 对象的消亡——HotSpot的设计细节
HotSpot 的细节实现 文章目录 HotSpot 的细节实现OopMap 与 根节点枚举根节点类型及说明HotSpot中的实现 OopMap 与 安全点安全点介绍如何保证程序在安全点上? 安全区域记忆集与卡表记忆集卡表 写屏障并发的可达性分析(与用户线程)并发可达性…...
)
vue 运行或打包过程报错 JavaScript heap out of memory(内存溢出)
安装 increase-memory-limit npm install increase-memory-limit 运行increase-memory-limit ./node_modules/.bin/increase-memory-limit 运行后会报以下错误: "node --max-old-space-size10240" 不是内部或外部命令,也不是可运行的程序…...

git分支提交方法
先下载最新代码 改动文件覆盖 cp 文件到~/file/ git add添加文件 git commit提交本地 建立分支 git diff .c git status -uno git add git commit git checkout -b issue-lyd git push origin issue-lyd...
从微架构到向量化--CPU性能优化指北
引入 定位程序性能问题,相信大家都有很多很好的办法,比如用top/uptime观察负载和CPU使用率,用dstat/iostat观察io情况,ptrace/meminfo/vmstat观察内存、上下文切换和软硬中断等等,但是如果具体到CPU问题,我…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
