基于改进拥挤距离的多模态多目标优化差分进化(MMODE-ICD)求解无人机三维路径规划(MATLAB代码)
一、无人机多目标优化模型
无人机三维路径规划是无人机在执行任务过程中的非常关键的环节,无人机三维路径规划的主要目的是在满足任务需求和自主飞行约束的基础上,计算出发点和目标点之间的最佳航路。
1.1路径成本
无人机三维路径规划的首要目标是寻找起飞点和目标点之间最短路程的飞行路径方案。一般地,记无人机的飞行路径点为 W i j = ( x i j , y i j , z i j ) W_{i j}=\left(x_{i j}, y_{i j}, z_{i j}\right) Wij=(xij,yij,zij)即在第 i i i 条飞行路径中第 j j j个路径点的无人机三维空间位置,则整条飞行路径 X i X_{i} Xi 可表示为包含 n n n 个路径点的三维数组。将 2 个路径点之间的欧氏距离记作路径段 ∥ W i j W i , j + 1 → ∥ \left\|\overrightarrow{W_{i j} W_{i, j+1}}\right\| WijWi,j+1 ,则与无人机飞行路径成本函数 F 1 F_{1} F1 为:
F 1 ( X i ) = ∑ j = 1 n − 1 ∥ W i j W i , j + 1 → ∥ F_{1}\left(X_{i}\right)=\sum_{j=1}^{n-1}\left\|\overrightarrow{W_{i j} W_{i, j+1}}\right\| F1(Xi)=j=1∑n−1 WijWi,j+1
1.2障碍物威胁成本
无人机通过躲避障碍物来确保安全作业航迹。设定障碍物威胁区为圆柱体形式,其投影如下图所示,记圆柱体中心坐标为 C k C_{k} Ck,半径为 R k R_{k} Rk,则无人机的避障威胁成本与其路径段 ∥ W i j W i , j + 1 → ∥ \left\|\overrightarrow{W_{i j} W_{i, j+1}}\right\| WijWi,j+1 和障碍物中心 C k C_{k} Ck的距离 d k d_{k} dk 成反比。

将飞行环境下的障碍物威胁区集合记作 T T T,则与无人机避障威胁相关的成本函数 F 2 F_{2} F2为:
F 2 ( X i ) = ∑ j = 1 n − 1 ∑ k = 1 K T k ( W i j W i , j + 1 → ) F_{2}\left(X_{i}\right)=\sum_{j=1}^{n-1} \sum_{k=1}^{K} T_{k}\left(\overrightarrow{W_{i j} W_{i, j+1}}\right) F2(Xi)=j=1∑n−1k=1∑KTk(WijWi,j+1)
其中:
T k ( W i j W i , j + 1 → ) = { 0 ( d k > R k ) ( R k / d k ) ( 0 < d k < R k ) ∞ ( d k = 0 ) T_{k}\left(\overrightarrow{W_{i j} W_{i, j+1}}\right)=\left\{\begin{array}{ll} 0 & \left(d_{k}>R_{k}\right) \\ \left(R_{k}/d_{k}\right) & \left(0<d_{k}<R_{k}\right) \\ \infty & \left(d_{k}=0\right) \end{array}\right. Tk(WijWi,j+1)=⎩ ⎨ ⎧0(Rk/dk)∞(dk>Rk)(0<dk<Rk)(dk=0)
1.3飞行高度威胁成本
无人机的飞行高度通常受到最小高度 h m i n h_{min} hmin 和最大高度 h m a x h_{max} hmax 的约束限制,如下图 所示,其中 T i j T_{ij} Tij 为地形的高度, Z i j Z_{ij} Zij为无人机相对于海平面的高度。

将无人机在路径点 W i j W_{ij} Wij处距离基准地形地面的高度记作 h i j h_{ij} hij,即 Z i j Z_{ij} Zij和 T i j T_{ij} Tij 的差,则与无人机当前路径点 W i j W_{ij} Wij相关的成本函数 H i j H_{ij} Hij 为:
H i j = { γ h ( h i j − h max ) ( h i j > h max ) 0 ( h min < h i j < h max ) γ h ( h min − h i j ) ( 0 < h i j < h min ) ∞ ( h i j < 0 ) H_{i j}=\left\{\begin{array}{ll} \gamma_{h}\left(h_{i j}-h_{\max }\right) & \left(h_{i j}>h_{\max }\right) \\ 0 & \left(h_{\min }<h_{i j}<h_{\max }\right) \\ \gamma_{h}\left(h_{\min }-h_{i j}\right) & \left(0<h_{i j}<h_{\min }\right) \\ \infty & \left(h_{i j}<0\right) \end{array}\right. Hij=⎩ ⎨ ⎧γh(hij−hmax)0γh(hmin−hij)∞(hij>hmax)(hmin<hij<hmax)(0<hij<hmin)(hij<0)
同时,将无人机飞行高度超出约束限制条件的惩罚系数记作 γ h γ_{h} γh,则与无人机飞行路径相关的成本函数 F 3 F_{3} F3为:
F 3 ( X i ) = ∑ j = 1 n H i j F_{3}\left(X_{i}\right)=\sum_{j=1}^{n} H_{i j} F3(Xi)=j=1∑nHij
1.4飞行转角威胁成本
无人机的飞行转角控制参数主要包括水平转弯角和竖直俯仰角,这 2 个参数变量必须符合无人机的实际转角约束限制,否则航迹规划模型无法生成具有可行性的飞行路径。如下图所示, ∥ W i j W i , j + 1 → ∥ \left\|\overrightarrow{W_{i j} W_{i, j+1}}\right\| WijWi,j+1 和 ∥ W i j + 1 W i , j + 2 → ∥ \left\|\overrightarrow{W_{i j+1} W_{i, j+2}}\right\| Wij+1Wi,j+2 表示无人机飞行路径中的 2 个连续路径段, W i j ′ W i , j + 1 ′ → \overrightarrow{W_{i j}^{\prime} W_{i, j+1}^{\prime}} Wij′Wi,j+1′和 W i j + 1 ′ W i , j + 2 ′ → \overrightarrow{W_{i j+1}^{\prime} W_{i, j+2}^{\prime}} Wij+1′Wi,j+2′是其在xoy 平面的投影。

记𝒌为轴正方向的单位向量,则 W i j + 1 ′ W i , j + 2 ′ → \overrightarrow{W_{i j+1}^{\prime} W_{i, j+2}^{\prime}} Wij+1′Wi,j+2′的计算式和水平转弯角 α i j α_{ij} αij、竖直俯仰角 β i , j + 1 β_{i,j+1} βi,j+1 计算式为:
W i j ′ W i , j + 1 ′ → = k × ( W i j W i , j + 1 → × k ) α i j = arctan ( W i j ′ W i , j + 1 ′ → × W i , j + 1 ′ W i , j + 2 ′ ‾ W i j ′ W i , j + 1 ′ → ⋅ W i , j + 1 ′ W i , j + 2 ′ ‾ ) β i j = arctan ( z i , j + 1 − z i j ∥ W i j ′ W i , j + 1 ′ → ∥ ) \begin{array}{c} \overrightarrow{W_{i j}^{\prime} W_{i, j+1}^{\prime}}=\boldsymbol{k} \times\left(\overrightarrow{W_{i j} W_{i, j+1}} \times \boldsymbol{k}\right) \\ \alpha_{i j}=\arctan \left(\frac{\overrightarrow{W_{i j}^{\prime} W_{i, j+1}^{\prime}} \times \overline{W_{i, j+1}^{\prime} W_{i, j+2}^{\prime}}}{\overrightarrow{W_{i j}^{\prime} W_{i, j+1}^{\prime}} \cdot \overline{W_{i, j+1}^{\prime} W_{i, j+2}^{\prime}}}\right) \\ \beta_{i j}=\arctan \left(\frac{z_{i, j+1}-z_{i j}}{\left\|\overrightarrow{W_{i j}^{\prime} W_{i, j+1}^{\prime}}\right\|}\right) \end{array} Wij′Wi,j+1′=k×(WijWi,j+1×k)αij=arctan(Wij′Wi,j+1′⋅Wi,j+1′Wi,j+2′Wij′Wi,j+1′×Wi,j+1′Wi,j+2′)βij=arctan Wij′Wi,j+1′ zi,j+1−zij
同时,将无人机的水平转弯角和竖直俯仰角超出约束限制条件的惩罚系数分别记作 a 1 = 1 a_{1}=1 a1=1和 a 2 = 1 a_{2}=1 a2=1,则与无人机飞行转角相关的成本函数 F 4 F_{4} F4 为:
F 4 ( X i ) = a 1 ∑ j = 1 n − 2 α i j + a 2 ∑ j = 1 n − 1 ∣ β i j − β i , j − 1 ∣ F_{4}\left(X_{i}\right)=a_{1} \sum_{j=1}^{n-2} \alpha_{i j}+a_{2} \sum_{j=1}^{n-1}\left|\beta_{i j}-\beta_{i, j-1}\right| F4(Xi)=a1j=1∑n−2αij+a2j=1∑n−1∣βij−βi,j−1∣
1.5无人机三维路径规划的目标函数
综合考虑与无人机飞行路径 X i X_{i} Xi 相关的最短路径成本、最小威胁成本,以及飞行高度成本和飞行转角成本等限制,基于多因素约束的多目标函数构建如下:其中第一个目标函数 f 1 f_{1} f1为最短路径成本,第二个目标函数 f 2 f_{2} f2为最小威胁成本,为障碍物威胁成本、飞行高度威胁成本和飞行转角威胁成本的总和,具体定义如下为:
f 1 ( X i ) = F 1 ( X i ) f_{1}\left(X_{i}\right)=F_{1}\left(X_{i}\right) f1(Xi)=F1(Xi)
f 2 ( X i ) = F 2 ( X i ) + F 3 ( X i ) + F 4 ( X i ) f_{2}\left(X_{i}\right)=F_{2}\left(X_{i}\right)+F_{3}\left(X_{i}\right)+F_{4}\left(X_{i}\right) f2(Xi)=F2(Xi)+F3(Xi)+F4(Xi)
参考文献:
[1]吕石磊,范仁杰,李震,陈嘉鸿,谢家兴.基于改进蝙蝠算法和圆柱坐标系的农业无人机航迹规划[J].农业机械学报:1-19
[2]褚宏悦,易军凯.无人机安全路径规划的混沌粒子群优化研究[J].控制工程:1-8
[3]MD Phung, Ha Q P . Safety-enhanced UAV Path Planning with Spherical Vector-based Particle Swarm Optimization: 2021.
[4]陈明强,李奇峰,冯树娟等.基于改进粒子群算法的无人机三维航迹规划[J].无线电工程,2023,53(02):394-400.
[5]徐建新,孙纬,马超.基于改进粒子群算法的无人机三维路径规划[J].电光与控制:1-10
[6]骆文冠,于小兵.基于强化学习布谷鸟搜索算法的应急无人机路径规划[J].灾害学:1-10
[7]陈先亮,黄元君,范勤勤.基于多模态多目标进化算法的无人机三维路径规划[J].火力与指挥控制, 2023(11):32-39.
二、MMODE-ICD介绍
基于改进拥挤距离的多模态多目标优化差分进化(Differential Evolution Using Improved Crowding Distance for Multimodal Multiobjective Optimization,MMODE-ICD)是一种多模态多目标优化算法。在多目标优化问题中,通常假设决策空间和目标空间之间存在一一映射关系,但并非总是如此。在某些问题中,不同的变量可能具有相同或相似的目标值,这意味着存在多对一的映射。这种情况下,存在多个Pareto集合(PS)映射到相同的Pareto前沿(PF),这些问题被称为多模态多目标问题(MMOPs)。
MMODE-ICD算法原理
- 差分向量的生成:在提出的方法中,差分向量的生成考虑了决策空间和目标空间的多样性。
- 拥挤距离的计算:与其他方法不同,所提出的拥挤距离计算过程中考虑了所有选定个体,而不是单独考虑每个Pareto等级。决策空间中的拥挤距离被替换为与邻居的欧几里得距离的加权和。
- 环境选择过程:并非所有高等级个体都被选中,因为其中一些可能非常拥挤。相反,底层等级中的潜在解决方案有机会进化。通过这些操作,所提出的算法可以维持多模态多目标优化问题的多个PS,并提高决策和目标空间的多样性。
MMODE-ICD算法流程
- 初始化:初始化种群,并定义算法参数。
- 差分向量生成:根据决策空间和目标空间的拥挤距离自适应地选择父代来生成差分向量。
- 拥挤距离计算:重新设计拥挤距离的计算方法,以更好地反映真实的拥挤程度,并平衡多样性和收敛性。
- 环境选择:在环境选择阶段,不是简单地选择所有高等级个体,而是根据拥挤距离自适应地选择一定比例的个体。
- 迭代更新:通过上述步骤,更新种群,并重复迭代过程直到满足终止条件。
- 输出:最终输出Pareto最优解集。
参考文献:
[1] Yue C , Suganthan P N , Liang J ,et al.Differential Evolution Using Improved Crowding Distance for Multimodal Multiobjective Optimization[J].Swarm and Evolutionary Computation, 2021, 62(9):100849.DOI:10.1016/j.swevo.2021.100849.
三、MMODE-ICD求解无人机路径规划
3.1部分代码
close all
clear
clc
dbstop if all error
addpath("./MMODE-ICD/")
global model
model = CreateModel(); % 创建模型
MultiObj= fun_info();%获取无人机模型信息
params.maxgen=100; % 最大迭代次数
params.Np=100; % 种群大小
params.Nr=200; %外部存档大小(不得小于种群大小)
[Xbest,Fbest] = MMODE-ICD(params,MultiObj);3.2部分结果
MMODE-ICD求解得到的pareto前沿图:

MMODE-ICD求解得到的所有无人机路径图:



MMODE-ICD求解得到的路径成本最小和威胁成本最小的路径:



四、完整MATLAB代码
见下方联系方式
相关文章:

基于改进拥挤距离的多模态多目标优化差分进化(MMODE-ICD)求解无人机三维路径规划(MATLAB代码)
一、无人机多目标优化模型 无人机三维路径规划是无人机在执行任务过程中的非常关键的环节,无人机三维路径规划的主要目的是在满足任务需求和自主飞行约束的基础上,计算出发点和目标点之间的最佳航路。 1.1路径成本 无人机三维路径规划的首要目标是寻找…...

opencascade AIS_Trihedron源码学习 绘制三轴坐标系
opencascade AIS_Trihedron 前言 //! 创建一个可选择的三轴坐标系 //! 该三轴坐标系包括一个原点,三个轴线和三个标签。 //! 标签的默认文本为 “X”, “Y”, “Z”。 //! 可以更改原点和任意轴线的颜色,箭头和标签的颜色也可以改变。 //! 可视化呈现可…...

【C++】C++应用案例-通讯录管理系统
目录 一、整体介绍 1.1、需求和目标 1.2、整体功能描述 二、页面及功能描述 2.1 主菜单 2.2 添加联系人菜单 2.3 显示联系人菜单 2.4 修改联系人菜单 2.5 退出功能 三、流程设计 3.1 主流程 3.2 添加操作流程 3.3 显示联系人操作流程 3.4 修改联系人操作流程 四…...

使用Python自动批量提取增值税发票信息并导出为Excel文件
要批量提取增值税发票的关键信息并将其导出为 Excel 文件,可以使用 Python 脚本结合 pdfplumber(用于解析 PDF 内容)、pandas(用于处理数据并导出 Excel)等库来实现。以下是实现这一目标的详细步骤。 1. 环境设置 首…...

vitis (eclipse) 的Indexer不能搜索、不能跳转到函数和变量定义和声明不能打开调用层次的解决方法
在使用vitis(2021.1) 过程中,有一个非常方便实用的功能,就是在函数或变量等源代码上通过右键菜单或快捷键F3、F4、CtrlAltH,也可以按住Ctrl键然后鼠标停留在函数名或变量名上,点击出现的链接,可以跳转到函数或变量的定…...
最佳HR软件指南:11款高效管理工具
文章介绍了11款人力资源管理工具:Moka、友人才、北森HRSaaS、同鑫eHR、i人事、红海eHR、BambooHR、Skuad、Hibob、OrangeHRM、Verint。 在选择人力资源管理软件时,选错不仅浪费时间和金钱,还会影响团队的工作效率和员工满意度。本文总结了11款…...

家长为孩子出国留学择校的四个步骤
如何为孩子选择最好的学校?无论您是选择公立或私立学校还是在家上学,无论您是否支付学费,都必须仔细规划。在为孩子选择学校的过程中,以下部分有供您考虑的问题。 写下对你来说最重要的五件事 在考虑选择学校时,您可…...

数据挖掘可以挖掘什么类型的模式?
一、挖掘频繁模式、关联和相关性 频繁模式(frequent pettern)是在数据中频繁出现的模式。 频繁项集一般是指频繁的在事务数据集中一起出现的商品的集合。 频繁出现的子序列,如顾客倾向于先买相机,再买内存卡这样的模式就是一个…...

JAVA中的隐式参数this
在Java中,this 关键字是一个非常重要的隐式参数,它代表当前对象的引用。通过 this,你可以访问类中的字段(属性)、方法以及构造函数中的参数(当参数名与字段名相同时,用于区分)。虽然…...

ThreadLocal 使用和详解避坑
在多线程编程中,每个线程都有自己的线程栈和线程本地存储。线程栈用于存储方法调用的信息,而线程本地存储则是每个线程私有的存储空间,用于存储线程的局部变量。ThreadLocal类提供了一种简单的方式来实现线程本地存储,它允许将线程…...

Python中使用类方法的返回值在其他方法中继续调用,return self进行链式调用
文章目录 return self进行链式调用继续思考,以下内容可以不看如果self中没有初始化valueself中定义其他变量,调用类方法外的函数 return self进行链式调用 在Python中,可以使用类方法的返回值在其他方法中继续调用。这通常通过返回类实例&am…...

基于IOT架构的数据采集监控平台!
LP-SCADA数据采集监控平台是蓝鹏测控推出的一款聚焦于工业领域的自动化数据采集监控系统, 助力数字工厂建设的统一监控平台。 为企业提供从下到上的完整的生产信息采集与集成服务,从而为企业综合自动化、工厂数字化及完整的"管控一体化”的解决方案…...

初见scikit-learn之基础教程
初见scikit-learn之基础教程 scikit-learn 基础教程 1. scikit-learn 简介1.1 什么是 scikit-learn?1.2 scikit-learn 的主要功能 2. 安装 scikit-learn2.1 安装方法2.2 验证安装 3. scikit-learn 基本使用3.1 数据加载与预处理3.1.1 加载数据集3.1.2 数据拆分3.1.3…...

基于STM32的嵌入式深度学习系统教程
目录 引言环境准备嵌入式深度学习系统基础代码实现:实现嵌入式深度学习系统 数据采集与预处理深度学习模型训练与优化模型部署与推理实时数据处理与反馈应用场景:智能物联网设备常见问题与解决方案收尾与总结 引言 随着深度学习在各种应用中的广泛采用…...

hive udf去掉map中的一个或者多个key
实现一个hive udf,可以将Map中的某一个或者多个key去掉,这里要继承GenericUDF 这个抽象类,然后Override evaluate这个函数即可,可以把执行这个udf前初始化的一些内容放在initialize方法内,比如参数的判断,函数的返回值类型等等。 代码写好之后,可以用如下方法创建这个函…...
模型量化技术综述:揭示大型语言模型压缩的前沿技术
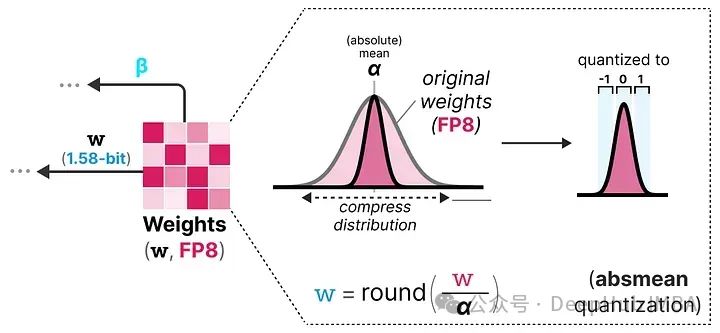
大型语言模型(LLMs)通常因为体积过大而无法在消费级硬件上运行。这些模型可能包含数十亿个参数,通常需要配备大量显存的GPU来加速推理过程。 因此越来越多的研究致力于通过改进训练、使用适配器等方法来缩小这些模型的体积。在这一领域中&am…...

一文掌握Prompt:万能框架+优化技巧+常用指标
👉目录 1 写在前面 2 Prompt 万能框架 3 框架的细化 4 在框架上增加更多信息(RAG) 5 让大模型更好的思考(CoT) 6 附加技巧 7 优化方式及常用指标 8 写在最后 随着大模型在2023年横空出世,“Prompt 工程” 应…...

Vue 常用组件间通信方式
Vue 常用组件间通信方式 1. 父子组件通信 1.1 Props 父组件通过 props 向子组件传递数据,子组件通过 props 接收数据。 <!-- ParentComponent.vue --> <template><ChildComponent :message"parentMessage"></ChildComponent>…...
NineData云原生智能数据管理平台新功能发布|2024年7月版
本月发布 12 项更新,其中性能优化 3 项、功能优化 8 项、安全性发布 1 项。 1. 性能优化 数据复制 - SQL Server 增量性能优化 调整读取和写入方式,让 SQL Server 增量复制的性能轻松达到 5000 RPS 以上。 数据复制 - Doris|SelectDB|StarRocks 性能优…...

验收测试:确保软件符合业务需求和合同要求
目录 前言1. 验收测试的概念1.1 用户验收测试(UAT)1.2 操作验收测试(OAT) 2. 验收测试的主要作用2.1 确认业务需求的满足2.2 验证合同要求的实现2.3 提升用户信心 3. 验收测试在整个测试中的地位3.1 测试的最后一道关卡3.2 用户与…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
