切比雪夫距离
切比雪夫距离(Chebyshev Distance),又称棋盘距离或最大值距离,是一种用于测量两个点之间距离的度量方法。在二维平面上,切比雪夫距离定义为两个点之间的最大坐标差值。其公式如下:
DChebyshev=max(∣x2−x1∣,∣y2−y1∣)DChebyshev=max(∣x2−x1∣,∣y2−y1∣)
对于高维空间,切比雪夫距离也可以拓展为:
DChebyshev=max(∣x2−x1∣,∣y2−y1∣,…,∣z2−z1∣)DChebyshev=max(∣x2−x1∣,∣y2−y1∣,…,∣z2−z1∣)
切比雪夫距离的一个常见例子是在国际象棋中,国王可以向八个方向移动,这个距离就等于国王从一个方格移动到另一个方格所需的最少步数。
相关文章:

切比雪夫距离
切比雪夫距离(Chebyshev Distance),又称棋盘距离或最大值距离,是一种用于测量两个点之间距离的度量方法。在二维平面上,切比雪夫距离定义为两个点之间的最大坐标差值。其公式如下: DChebyshevmax(∣x2−…...
教程 —— 第4章 计算机网络与Internet(下))
计算机基础(Windows 10+Office 2016)教程 —— 第4章 计算机网络与Internet(下)
第4章 计算机网络与Internet 4.4 局域网4.4.1 局域网概述4.4.2 以太网4.4.3 令牌环网4.4.4 无线局域网 4.5 Internet4.5.1 Internet 概述4.5.2 Internet 的基本概念4.5.3 Internet 的接入4.5.4 万维网 4.6 Internet的应用4.6.1 电子邮件4.6.2 文件传输4.6.3 搜索引擎 4.4 局域网…...

机器学习用Python还是R?哪个更好一些?
选择使用Python还是R来进行机器学习取决于多个因素,包括个人偏好、项目需求以及可用的资源。这里我可以简要比较一下它们的优缺点: Python的优势: 通用性和灵活性: Python是一种通用编程语言,可以用于多种用途&#…...
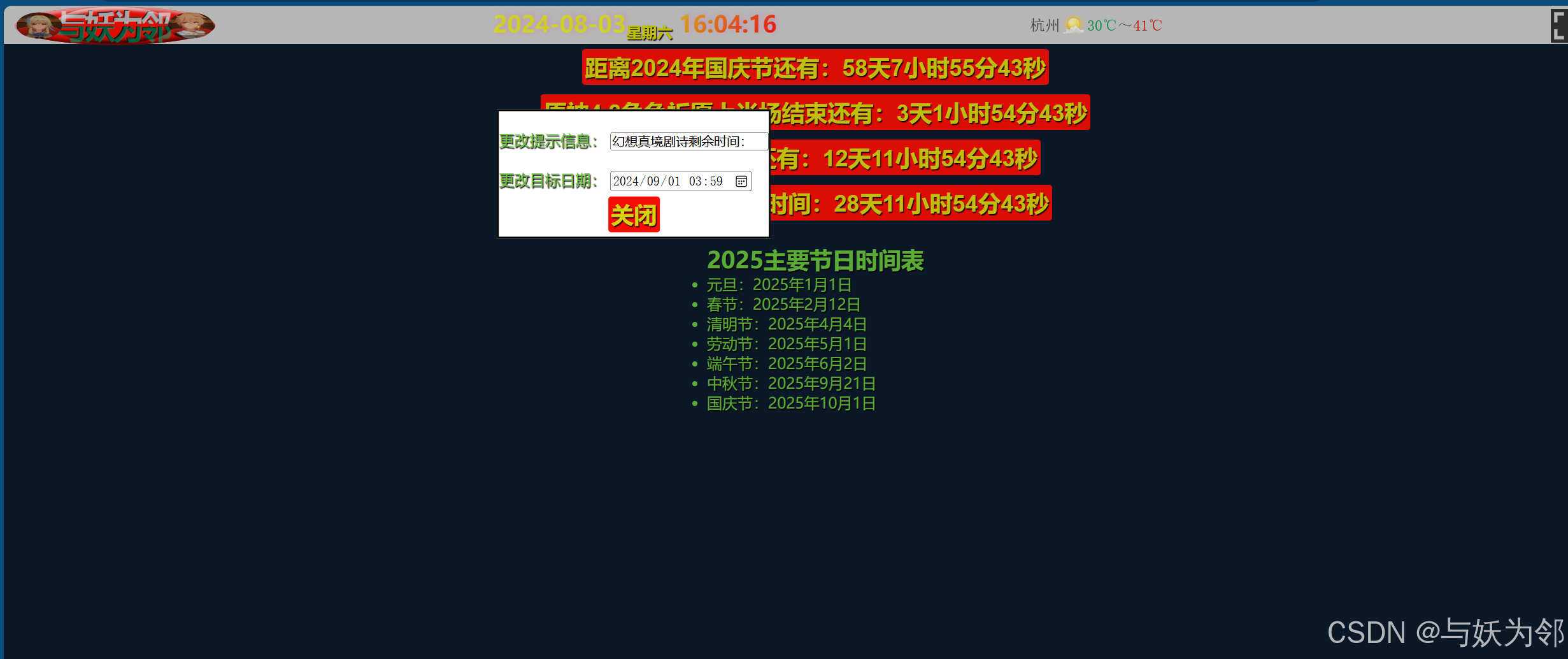
4个自定义倒计时
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><title>4个自定义倒计时</title><style>* {margin: 0;padding: 0;box-sizing: border-box;user-select: none;body {background: #0b1b2c;}}hea…...

linux系统编程中Shell脚本配置,及linux脚本中的man test
Shell脚本配置是指在脚本中设置各种参数、选项和环境,以确保脚本能够根据预期的需求和环境执行。配置可以包括变量设置、环境变量、命令选项和错误处理等。 1. 脚本开头的配置 Shebang 第一行通常是shebang,它告诉系统使用哪个解释器来执行脚本。例如…...

Win7虚拟机分享(已安装VMware Tools)
前言 之前写过VMware安装Win7并安装VMware tools的博客,但操作仍显繁琐。后来发现可以直接分享已经配置好的虚拟机,所有软件都是安装好的,解压即用。 一. VMware Win7虚拟机配置 已完成的配置和安装的软件 专业版Win7系统(已永久激活)VMware…...

CANOpen EMCY紧急报文介绍
什么是CANOpen紧急报文 CANOpen中的Emcy紧急报文用于当设备出现故障或警告时,向其它节点报告故障或警告使用的。如设备某个设备出现过压或过流时,就可以发送紧急报文。 紧急报文的格式 错误代码:是0x1003索引预定义错误字段的内容ÿ…...
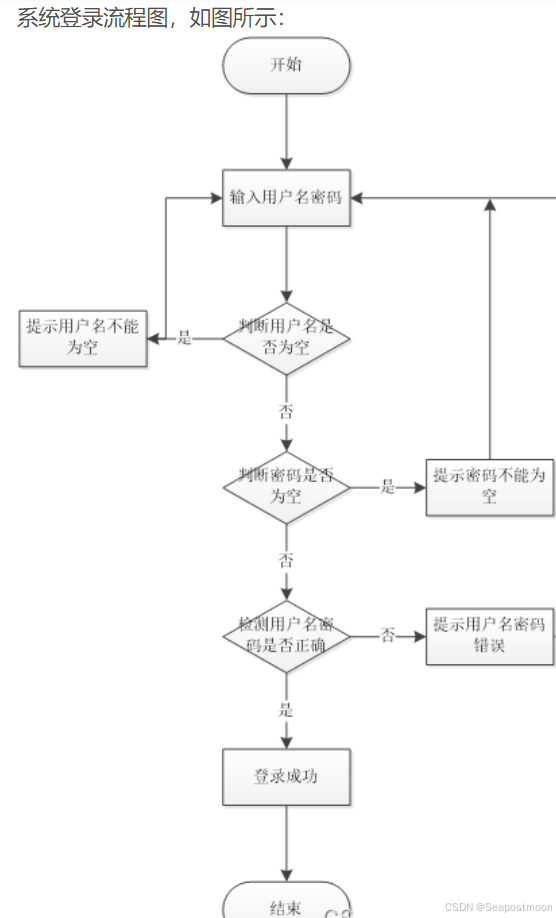
JAVA项目
目录 一、前言 二、技术介绍 三、项目实现流程 四、论文流程参考 五、核心代码截图 专注于大学生实战开发、讲解和毕业答疑等辅导,获取源码后台 一、前言 在数字化音乐时代,个性化推荐已成为提升用户体验、促进音乐消费的重要手段。为此࿰…...
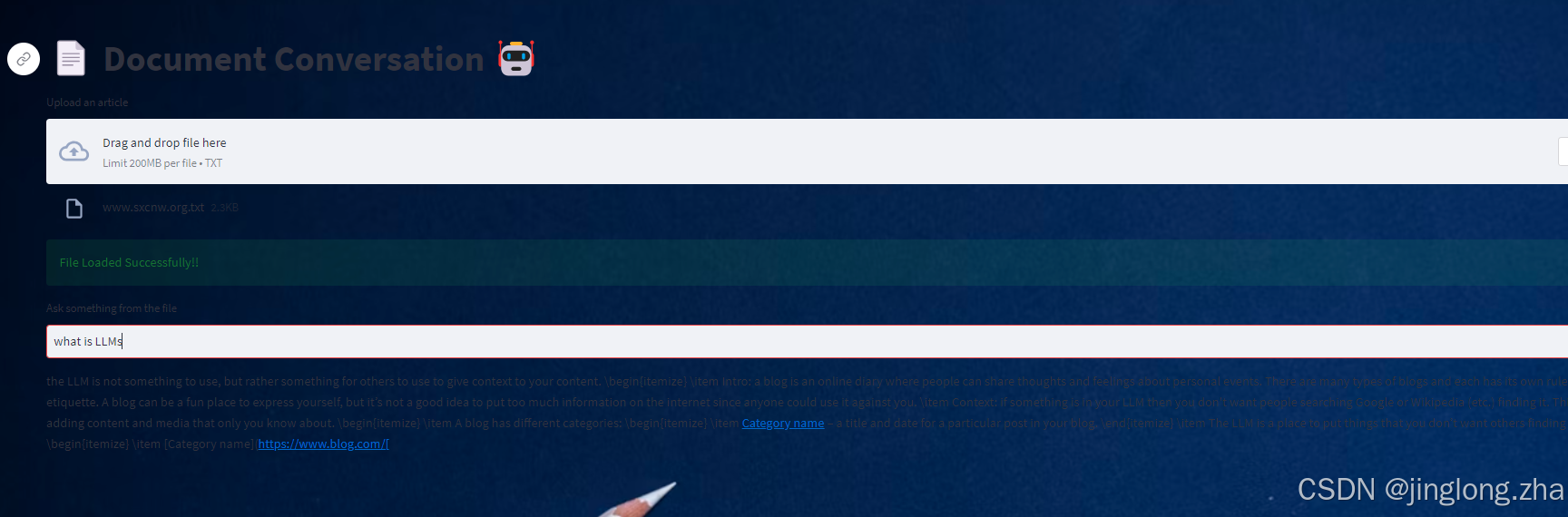
️ LangChain +Streamlit+ Llama :将对话式人工智能引入您的本地设备(下篇)
引言:种下一棵树最好的时间是十年前,其次是现在 书接上回:将对话式人工智能引入您的本地设备成为可能CSDNhttps://mp.csdn.net/mp_blog/creation/editor/140865426 目的:在这个大模型横行的时候,我们常用电脑如何开展大模型的工作…...
)
Kafka实战(Scala操作)
Kafka基础讲解部分 Kafka基础讲解部分 Kafka实战(Scala操作) 1、引入依赖 版本: <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding> <project.reporting.outputEncoding>UTF-8</project.report…...
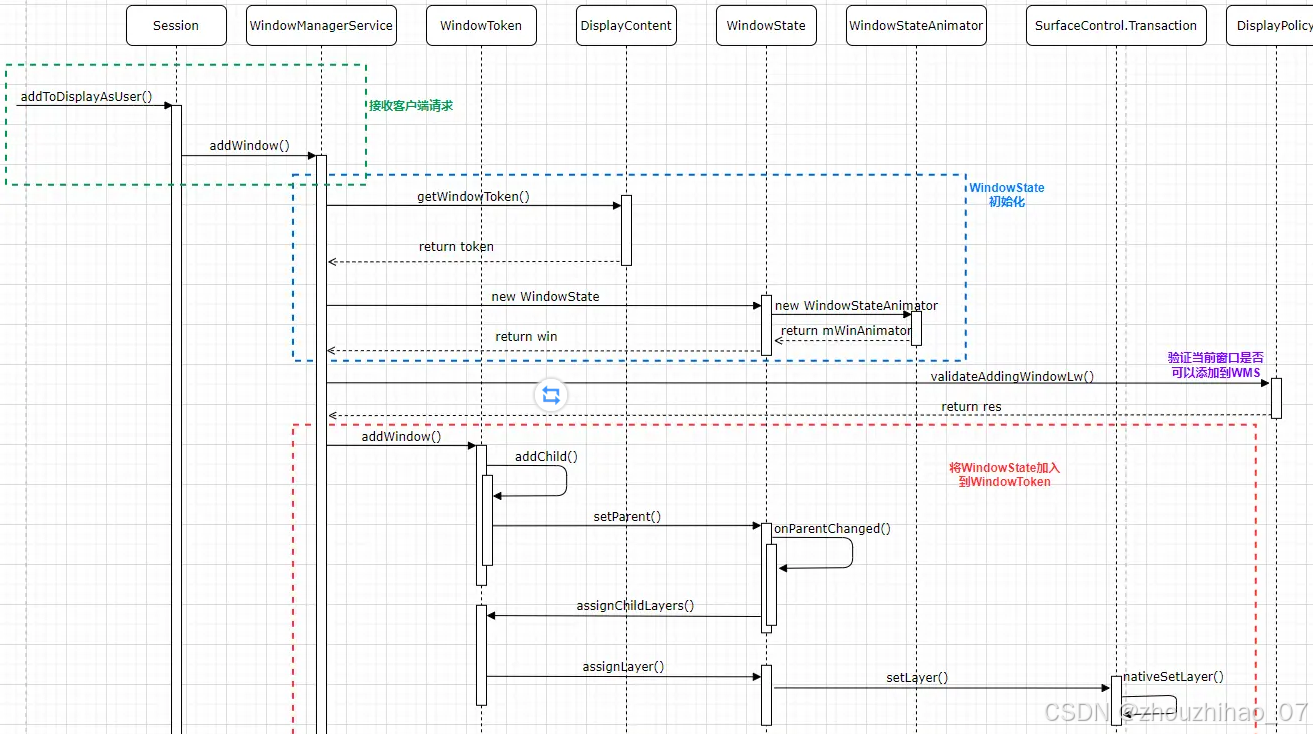
Android Framework 之WMS详解
1.WMS说的就是 WindowManagerService:负责为Activity对应的窗口分配Surface,管理Surface的显示顺序以及位置尺寸,控制窗口动画 。 它是Android系统中为各个客户端即每个app来提供这样的服务的一个类。 在Android系统中在systemServer 进程和各…...

opencv-图像仿射变换
仿射变换设计图像位置角度的变化,是深度学习预处理中常用的功能。仿射变换就是对图像的平移缩放旋转翻转操作的组合 如下图,对图中点1,2,3与图二中三个点一一映射,仍然形成三角形,但形状已经发生改变,通过这两组三点求…...
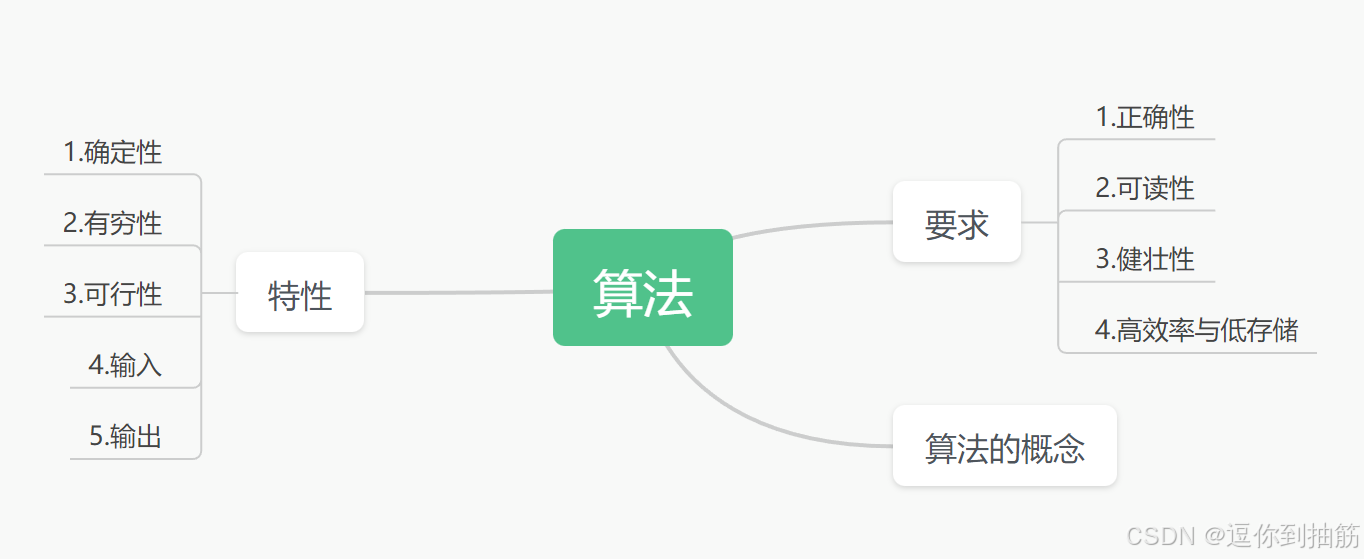
算法的基本概念
一、算法的基本概念思维导图 二、什么是算法: 1.我们知道数据结构就是将我门现实的世界中的问题数据化,存入计算机中,并实现对数据结构的一些基本操作。 2.算法就是如何处理这些存入计算机中的信息,以求高效的解决实际问题。 3…...
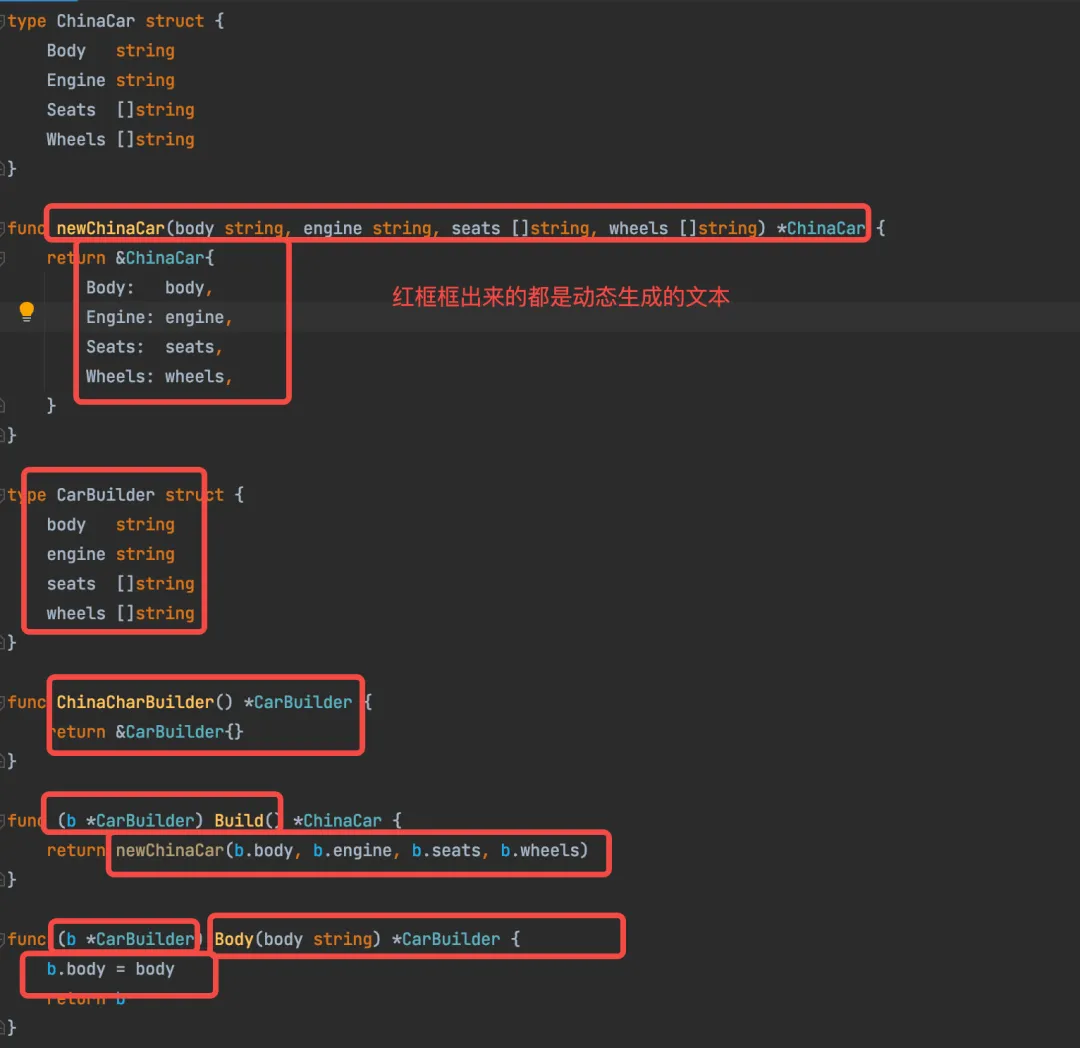
124. Go Template应用实例:用代码生成代码
文章目录 生成器模式生成器代码生成 本文用生成器模式作为例子,来演示如何用代码生成代码。 生成器模式 熟悉 Java 开发的同学都知道,lombok 有一个著名的注解 Builder ,只要加在类上面,就可以自动生成 Builder 模式的代码。如下…...

【AI实践】阿里云方言文本转语音TTS
最近要做一些普通话和方言demo 找一个免费工具 免费在线文字转语音工具 | edge-tts 在线体验 (bingal.com) 还有一些方言在阿里云上找了下,基于官方demo改了一下 阿里云语音合成接口说明_智能语音交互(ISI)-阿里云帮助中心 (aliyun.com) 如何下载安装、使用语音…...

java 之 各类日期格式转换
一、前言 大家在开发过程中必不可少得和日期打交道,对接别的系统时,时间日期格式不一致,每次都要转换! 从 Java1 到 Java8 将近 20 年,再加上 Java8 的普及时间、各种历史 API 兼容过渡时间。我们很多时候需要在旧时间 API 与新时…...

Nvidia黄仁勋对话Meta扎克伯格:AI和下一代计算平台的未来 | SIGGRAPH 2024对谈回顾
在今年的SIGGRAPH图形大会上,Nvidia创始人兼CEO黄仁勋与Meta创始人马克扎克伯格进行了一场长达60分钟的对谈。这场对话不仅讨论了AI的未来发展和Meta的开源哲学,还发布了不少新产品,并深入探讨了下一代计算平台的可能性。 引言 人工智能的发…...

【JAVA设计模式】适配器模式——类适配器模式详解与案例分析
前言 在软件设计中,适配器模式(Adapter Pattern)是一种结构型设计模式,旨在使不兼容的接口能够协同工作。它通过引入一个适配器类,帮助两个接口之间进行适配,使得它们能够互相操作。本文将详细介绍适配器模…...

【Vue】全局组件和局部组件
一、全局组件 定义: 全局组件是在整个Vue应用中都可以使用的组件。它们被注册在Vue的根实例上,因此可以在任何子组件的模板中被引用,而无需在每个组件中重复注册。 注册方式: 全局组件通过Vue.component方法进行注册。这个方法接…...

react引入高德地图并初始化卫星地图
react引入高德地图并初始化卫星地图 1.安装依赖 yarn add react-amap amap/amap-jsapi-loader2.初始化地图 import AMapLoader from "amap/amap-jsapi-loader"; import { FC, useEffect, useRef, useState } from "react";const HomeRight () > {con…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
