LeetCode 第136场双周赛个人题解
Q1. 求出胜利玩家的数目
原题链接
Q1. 求出胜利玩家的数目
思路分析
直接模拟
时间复杂度:O(N)
AC代码
class Solution {
public:int winningPlayerCount(int n, vector<vector<int>>& pick) {unordered_map<int, unordered_map<int, int>> cnt;for (auto& v : pick) {cnt[v[0]][v[1]] ++;}int res = 0;for (auto& [x, u] : cnt) {for (auto [c, d] : u) {if (x == 0 || d > x) {++ res;break;}}}return res;}
};Q2. 最少翻转次数使二进制矩阵回文 I
原题链接
Q2. 最少翻转次数使二进制矩阵回文 I
思路分析
直接贪心就行,计算原矩阵和转置矩阵的每一行的不同的两两对称位置的数目,取小的那个
时间复杂度:O(MN)
AC代码
class Solution:def minFlips(self, grid: List[List[int]]) -> int:res1 = 0for row in grid:n = len(row)l, r = 0, n - 1while l < r:res1 += 1 if row[l] != row[r] else 0l += 1r -= 1grid = list(zip(*grid))res2 = 0for row in grid:n = len(row)l, r = 0, n - 1while l < r:res2 += 1 if row[l] != row[r] else 0l += 1r -= 1return min(res1, res2)Q3. 最少翻转次数使二进制矩阵回文 II
原题链接
Q3. 最少翻转次数使二进制矩阵回文 II
思路分析
思维+分组背包
左上左下右上右下关于原点对称,所以矩阵只要满足回文,这四部分中1的数目一定是4的倍数
我们只需考虑行列为奇数的时候横对称轴和竖对称轴的情况
同样对两个对称轴的两两对称位置遍历,他们最终的结果要么是两个1要么是两个0,两个0的代价就是2 - 他们的和,两个1的代价也是2 - 他们的和
我们发现这就是一个分组背包问题,最多(n + m) / 2个组,每组内2个物品,背包容量为4
我们处理完四个对称部分的调整次数后,对横对称轴和竖对称轴求分组背包即可
时间复杂度:O(NM + N + M)
AC代码
class Solution:def minFlips(self, grid: List[List[int]]) -> int:res = c = 0m, n = len(grid), len(grid[0])buf = []res = 0for i in range(m // 2):for j in range(n // 2):s = grid[i][j] + grid[m - 1 - i][j] + grid[i][n - 1 - j] + grid[m - 1 - i][n - 1- j]res += min(4 - s, s)if m % 2:row = grid[m // 2]l, r = 0, n - 1while l < r:s = row[l] + row[r]buf.append([[0, s], [2, abs(2 - s)]])l += 1r -= 1if n % 2:l, r = 0, m - 1while l < r:s = grid[l][n // 2] + grid[r][n // 2]buf.append([[0, s], [2, abs(2 - s)]])l += 1r -= 1if m % 2 and n % 2:t = grid[m // 2][n // 2]buf.append([[t, 0], [0, t]])if not buf:return resf = [inf, inf, inf, inf]for r in buf:nf = f.copy()for j in range(4):mi = inffor x, v in r:t = ((j - x) % 4 + 4) % 4if nf[x % 4] == inf:f[x % 4] = min(f[x % 4], v)mi = min(nf[t] + v, mi)if nf[j] == inf:f[j] = min(f[j], mi)else:f[j] = mireturn res + f[0]Q4. 标记所有节点需要的时间
原题链接
Q4. 标记所有节点需要的时间
思路分析
换根dp
很明显的换根dp,为什么呢?
0时刻从根节点开始标记所需时间取决于根节点的孩子和根节点的奇偶性
而且题目要我们求出每个结点作为根时的情况,自然想到换根dp
先一次dfs0预处理d[],d[u] 代表0时刻开始标记u,u所在子树全部搞定的时间
然后dfs1 进行换根
求u 的儿子结点中 d[v] + (v & 1 ? 1 : 2)的最大值和次大值fi, se
那么我们换根为v时,如果d[v] + (v & 1 ? 1 : 2) == fi, 那么换根后d[u] = se,否则为fi
时间复杂度:O(N)
AC代码
class Solution:def timeTaken(self, edges: List[List[int]]) -> List[int]:n = len(edges) + 1adj = [[] for _ in range(n)]for x, y in edges:adj[x].append(y)adj[y].append(x)d = [0] * ndef dfs0(u: int, p: int) -> None:for v in adj[u]:if v == p:continuedfs0(v, u)d[u] = max(d[u], d[v] + (1 if v % 2 else 2))dfs0(0, -1)ans = [0] * ndef dfs1(u: int, p: int) -> None:fi, se = 0, 0for v in adj[u]:if d[v] + (1 if v % 2 else 2) > fi:se = fifi = d[v] + (1 if v % 2 else 2)elif d[v] + (1 if v % 2 else 2) > se:se = d[v] + (1 if v % 2 else 2)ans[u] = fifor v in adj[u]:if v == p:continued[u] = se if d[v] + (1 if v % 2 else 2) == fi else fidfs1(v, u)dfs1(0, -1)return ans相关文章:

LeetCode 第136场双周赛个人题解
Q1. 求出胜利玩家的数目 原题链接 Q1. 求出胜利玩家的数目 思路分析 直接模拟 时间复杂度:O(N) AC代码 class Solution { public:int winningPlayerCount(int n, vector<vector<int>>& pick) {unordered_map<int, unordered_map<int, …...

The operation was rejected by your operating system. code CERT_HAS_EXPIRED报错解决
各种报错,试了清缓存,使用管理员权限打开命令行工具,更新npm,都不好使 最终解决:删除 c:/user/admin/ .npmrc...

[Git][基本操作]详细讲解
目录 1.创建本地仓库2.配置 Git3.添加文件1.添加文件2.提交文件3.其他 && 说明 4.删除文件5.跟踪修改文件6.版本回退7.撤销修改0.前言1.未add2.已add,未commit3.已add,已commit 1.创建本地仓库 创建⼀个Git本地仓库:git init运行该命…...

springMVC中从Excel文件中导入导出数据
目录 1. 数据库展示2. 导入依赖3. 写方法3.1 导入数据3.2 导出数据 4. 效果5. 不足6. 参考链接 1. 数据库展示 2. 导入依赖 pom.xml <!--文件上传处理--><dependency><groupId>commons-io</groupId><artifactId>commons-io</artifactId>&…...

C++的STL简介(三)
目录 1.vector的模拟实现 1.1begin() 1.2end() 1.3打印信息 1.4 reserve() 1.5 size() 1.6 capacity() 1.7 push_back() 1.8[ ] 1.9 pop_back() 1.10 insert&…...

BERT模型
BERT模型是由谷歌团队于2019年提出的 Encoder-only 的 语言模型,发表于NLP顶会ACL上。原文题目为:《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》链接 在前大模型时代,BERT模型可以算是一个参数量比…...
技术的优势和挑战)
举例说明计算机视觉(CV)技术的优势和挑战
计算机视觉(CV)技术是通过计算机模拟和处理图像与视频数据来模拟人类视觉的能力。它可以带来许多优势,也面临一些挑战。 优势: 自动化:CV技术可以自动处理大量的图像和视频数据,从而提高工作效率和准确性。…...
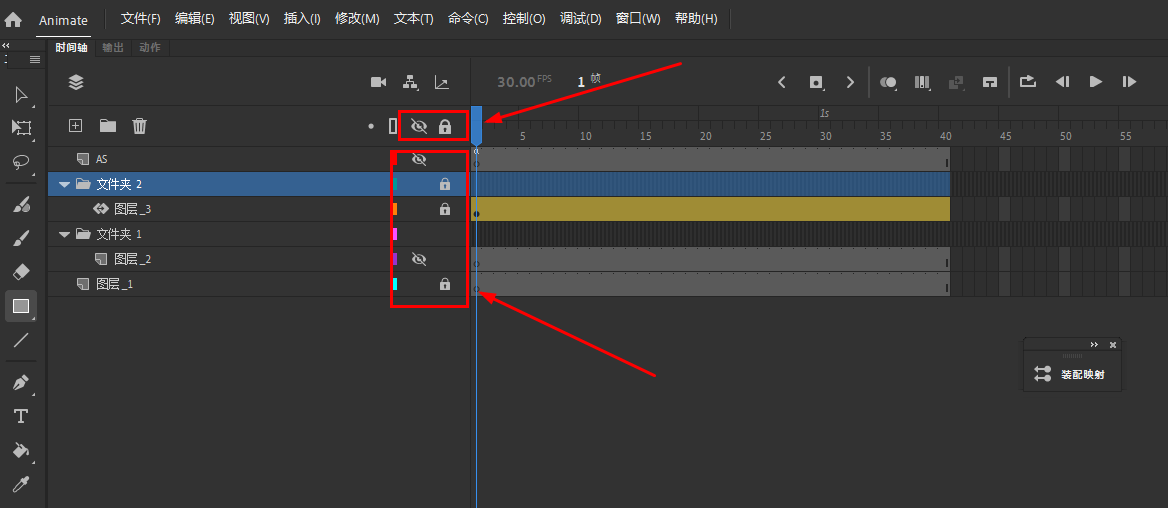
Animate软件基础:关于补间动画中的图层
Animate 文档中的每一个场景都可以包含任意数量的时间轴图层。使用图层和图层文件夹可组织动画序列的内容和分隔动画对象。在图层和文件夹中组织它们可防止它们在重叠时相互擦除、连接或分段。若要创建一次包含多个元件或文本字段的补间移动的动画,请将每个对象放置…...

mac|安装hashcat(压缩包密码p解)
一、安装Macports(如果有brew就不用这一步) 根据官网文档:The MacPorts Project -- Download & Installation,安装步骤如下 1、下载MacPorts,这里我用的是tar.gz ,可以通过keka(keka安装在…...

【保姆级系列:锐捷模拟器的下载安装使用全套教程】
保姆级系列:锐捷模拟器的下载安装使用全套教程 1.介绍2.下载3.安装4.实践教程5.验证 1.介绍 锐捷目前可以通过EVE-NG来模拟自己家的路由器,交换机,防火墙。实现方式是把自己家的镜像导入到EVE-ng里面来运行。下面主要就是介绍如何下载镜像和…...

virtualbox7安装centos7.9配置静态ip
1.背景 我大概在一年之前安装virtualbox7centos7.9的环境,但看视频说用vagrant启动的窗口可以不用第三方工具(比如xshell、secure等)连接centos7.9,于是尝鲜试了下还可以,导致系统文件格式是vmdk了(网上有vmdk转vdi的方法…...

结构型设计模式:桥接/组合/装饰/外观/享元
结构型设计模式:适配器/代理 (qq.com)...

vLLM初识(一)
vLLM初识(一) 前言 在LLM推理优化——KV Cache篇(百倍提速)中,我们已经介绍了KV Cache技术的原理,从中我们可以知道,KV Cache本质是空间换时间的技术,对于大型模型和长序列…...

【Apache Doris】周FAQ集锦:第 18 期
【Apache Doris】周FAQ集锦:第 18 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目! 在这个栏目中,每周将筛选社区反馈的热门问题和话题,重点回答并进行深入探讨。旨在为广大用户…...

docker部署可执行的jar
1.将项目打包,上传到服务器的指定目录 2.在该目录下创建Dockerfile文件 3.Dockerfile写入如下指令 # 基于哪个镜像 FROM java:8 # 拷贝文件到容器,也可以直接写成ADD xxxxx.jar /app.jar ADD springboot-file-0.0.1.jar file.jar RUN bash -c touch /…...

OpenCV||超详细的图像处理模块
一、颜色变换cvtColor dst cv2.cvtColor(src, code[, dstCn[, dst]]) src: 输入图像,即要进行颜色空间转换的原始图像。code: 转换代码,指定要执行的颜色空间转换类型。这是一个必需的参数,决定了源颜色空间到目标颜色空间的转换方式。dst…...

java面向对象期末总结
子类父类方法执行顺序?多态中和子类打印不一样; 子类在实现父类方法的时候没有用super关键字进行调用也会先执行父类的构造方法吗? 是的,当子类实例化时,先执行父类的构造方法,再执行子类的构造方法。即使在…...

文件搜索 36
删除文件 文件搜索 package File;import java.io.File;public class file3 {public static void main(String[] args) {search(new File("D :/"), "qq");}/*** 去目录搜索文件* param dir 目录* param filename 要搜索的文件名称*/public static void sear…...

IO多路转接
文章目录 五种IO模型fcntl多路转接selectpollepollepoll的工作模式 五种IO模型 阻塞IO: 在内核将数据准备好之前, 系统调用会一直等待. 所有的套接字, 默认都是阻塞方式.阻塞IO是最常见的IO模型。非阻塞IO: 如果内核还未将数据准备好, 系统调用仍然会直接返回, 并且返回EWOULD…...

基于深度学习的面部表情分类识别系统
:温馨提示:文末有 CSDN 平台官方提供的学长 QQ 名片 :) 1. 项目简介 面部表情识别是计算机视觉领域的一个重要研究方向, 它在人机交互、心理健康评估、安全监控等领域具有广泛的应用。近年来,随着深度学习技术的快速发展…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
