灵茶八题 - 子序列 +w+
灵茶八题 - 子序列 +w+
题目描述
给你一个长为 n n n 的数组 a a a,输出它的所有非空子序列的元素和的元素和。
例如 a = [ 1 , 2 , 3 ] a=[1,2,3] a=[1,2,3] 有七个非空子序列 [ 1 ] , [ 2 ] , [ 3 ] , [ 1 , 2 ] , [ 1 , 3 ] , [ 2 , 3 ] , [ 1 , 2 , 3 ] [1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] [1],[2],[3],[1,2],[1,3],[2,3],[1,2,3],元素和分别为 1 , 2 , 3 , 3 , 4 , 5 , 6 1,2,3,3,4,5,6 1,2,3,3,4,5,6,所以答案为 1 + 2 + 3 + 3 + 4 + 5 + 6 = 24 1+2+3+3+4+5+6=24 1+2+3+3+4+5+6=24。
由于答案很大,你需要输出答案模 1 0 9 + 7 10^9+7 109+7 后的结果。
输入格式
第一行输入一个整数 n ( 1 ≤ n ≤ 2 ⋅ 1 0 5 ) n\ (1\le n \le 2\cdot 10^5) n (1≤n≤2⋅105)。
第二行输入 n n n 个整数,表示数组 a a a 中的元素 ( 0 ≤ a [ i ] ≤ 1 0 9 ) (0\le a[i] \le 10^9) (0≤a[i]≤109)。
输出格式
一个整数,表示 a a a 的所有非空子序列的元素和的元素和,模 1 0 9 + 7 10^9+7 109+7 后的结果。
样例 #1
样例输入 #1
3
1 2 3
样例输出 #1
24
提示
对于子序列, 每一个出现的次数为2的n - 1次方
#include<bits/stdc++.h>using namespace std;typedef long long ll;
typedef pair<int, int>PII;
const int N=2e5+10;
const int MOD = 1e9 + 7;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e7 + 10;int t;int main()
{int n;cin >> n;ll res = 0;//对于子序列,每个元素出现的次数为2的n - 1次方for(int i = 1; i <= n; i ++){int x;cin >> x;res += x;}for(int i = 1; i <= n - 1; i ++){res = res * 2 % MOD;}cout << res << endl;return 0;
}
相关文章:

灵茶八题 - 子序列 +w+
灵茶八题 - 子序列 w 题目描述 给你一个长为 n n n 的数组 a a a,输出它的所有非空子序列的元素和的元素和。 例如 a [ 1 , 2 , 3 ] a[1,2,3] a[1,2,3] 有七个非空子序列 [ 1 ] , [ 2 ] , [ 3 ] , [ 1 , 2 ] , [ 1 , 3 ] , [ 2 , 3 ] , [ 1 , 2 , 3 ] [1],[…...

为什么美元债务会越来越多?
美元债务规模持续膨胀,其背后原因复杂多样,可归结为以下几个主要因素: 财政赤字和刺激政策是导致美元债务增加的重要原因。美国政府长期面临财政赤字问题,支出远超收入,为弥补这一缺口,政府不得不大量发行…...

二维凸包算法 Julia实现
问题描述:给定平面上 n n n 个点的集合 Q Q Q,求其子集 P P P 构成 Q Q Q 的凸包,即 ∀ p ∈ Q , ∃ p 0 , p 1 , p 2 ∈ P \forall p \in Q, \exist p_0, p_1, p_2 \in P ∀p∈Q,∃p0,p1,p2∈P 使得点 p p p 在以点 p 0 , p 1 …...
python dash框架
Dash 是一个用于创建数据分析型 web 应用的 Python 框架。它由 Plotly 团队开发,并且可以用来构建交互式的 web 应用程序,这些应用能够包含图表、表格、地图等多种数据可视化组件。 Dash 的特点: 易于使用:Dash 使用 Python 语法…...

2.外部中断(EXTI)
理论 NVIC:嵌套向量中断控制器(解释教程) 外部通用中断线(EXTI0~EXTI15):每个GPIO设置成中断模式,与中断控制器连接的线 外部中断触发方式 上升沿触发、下降沿触发、双边沿触发 外部中断触发函数 在stm32f1xx_it.c文件…...

Python | SyntaxError: invalid syntax 深度解析
Python | SyntaxError: invalid syntax 深度解析 在Python编程中,SyntaxError: invalid syntax是一个常见的错误,它表明Python解释器在尝试解析代码时遇到了语法问题。这个错误通常是由于代码中存在拼写错误、缺少符号(如括号、冒号或逗号&a…...
付费进群系统源码原版最新修复全开源版
付费进群,和平时所见到的别人拉你进群是不一样的,付费进群需要先缴费以后,才会看到群的二维码,扫码进群或者是长按二维码图片识别进群,付费进群这个功能广泛应用于拼多多的砍价群,活动的助力群,…...

Docker容器部署的SpringBoot项目jar包,上传文件但是找不到路径的问题
在docker容器内部署的jar包运行后,请求访问都没有问题,在文件上传时,发现上传图片接口响应成功,但是图片路径报404错误,发现找不到路径。 在服务器上查看也没有找到相关图片。 原因: 启动docker镜像时没…...
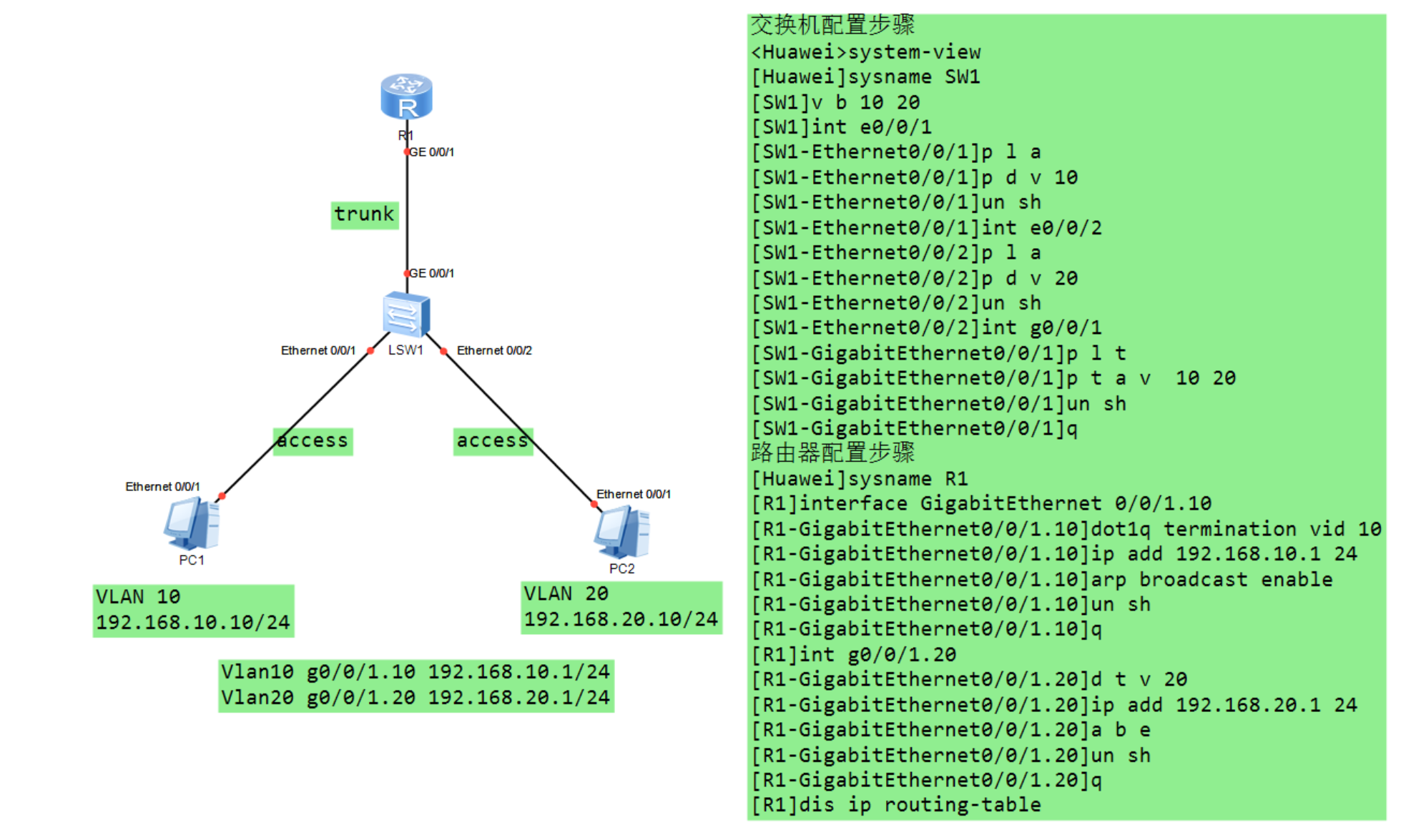
云计算学习——5G网络技术
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 Day1 网络参考模型 Day2 网络综合布线与应用 Day3 IP地址 Day4 华为eNSP网络设备模拟器的基础安装及简单使用 Day5 交换机的基本原理与配置 Day6 路由器的原理与配置 Day7 网络层协议介绍一 Day8 传…...

matlab仿真 信道编码和交织(上)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第八章内容,有兴趣的读者请阅读原书) clear all N10;%信息比特的行数 n7;%hamming码组长度n2^m-1 m3;%监督位长度 [H,G]hammgen(m);%产生(n,n-…...

基于YOLOv8的高压输电线路异物检测系统
基于YOLOv8的高压输电线路异物检测系统 (价格88) 包含 【“鸟窝”,“风筝”,“气球”,“垃圾”】 4个类 通过PYQT构建UI界面,包含图片检测,视频检测,摄像头实时检测。 (该系统可以根据数…...

23款奔驰GLS450加装原厂电吸门配置,提升车辆舒适性和便利性
今天是一台22款奔驰GLS450,车主是佛山的 以前被不良商家坑了 装了副厂的电吸门 刚开始就很正常 用了半年之后 就开始开不了门,被锁在里面,刚开始车主以为是零件坏了 后来越来越频繁,本来是为了家里老人小孩关门方便而升级的&#…...

git操作流程笔记
1、在本地项目文件夹右击鼠标点击Git Bash Here 2、输入git init,这个目录变成git可以管理的仓库,会出现一个.git文件夹,如果没出现的话需要选择“显示隐藏文件”(不会的同学自行百度一下) 3、绑定本地仓库与远程仓库…...

【QT】常用控件-上
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 目录 👉🏻QWidgetenabledgeometryrect制作上下左右按钮 window frame 的影响window titlewindowIcon代码示例: 通过 qrc 管理图片作为图标 windowOpacitycursor使用qrc自…...
帮助网站提升用户参与度的5个WordPress插件
仅靠编写精彩的内容、设计精美的图像和创建简化的客户旅程不足以提高网站参与度。您需要让用户在首次访问后继续与您的网站互动并成为回访者,才能真正吸引您所追求的兴趣。 幸运的是,对于 WordPress 用户来说,有数百种工具可用于提高用户参与…...

理解 Python 中的 @wraps:保留函数元数据
一.介绍 在本文中,我们将了解 wraps。在 Python 中使用装饰器时,您可能会遇到原始函数的元数据丢失的情况。这时,functools 模块中的 wraps 装饰器就可以派上用场了。让我们深入了解 wraps 的作用及其重要性。 二.简单装饰器的问题 首先&a…...
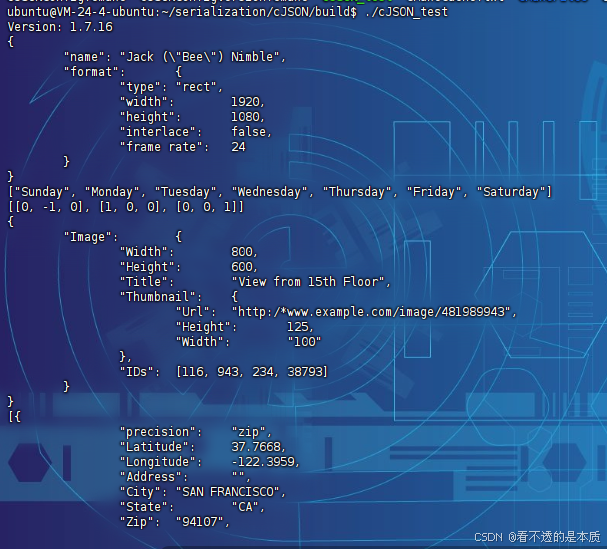
cjson
文章目录 概述编译cjson_test 小结 概述 在网络传输中,网络数据序列化,常用的有那么几种,json,protobuf都是很常用的,这一篇来写下json。 Json常用的有几个,rapidjson,jsoncpp,还有…...

Docker data root 目录更改
有时候受限于系统根目录空间的限制,需要将 docker data root 目录更改为其它目录,如单独挂载一个磁盘或存储。本篇文章介绍如何操作。 修改docker 工作目录 修改配置文件/etc/docker/daemon.json(在19.x 版本之前使用grapth) {&q…...
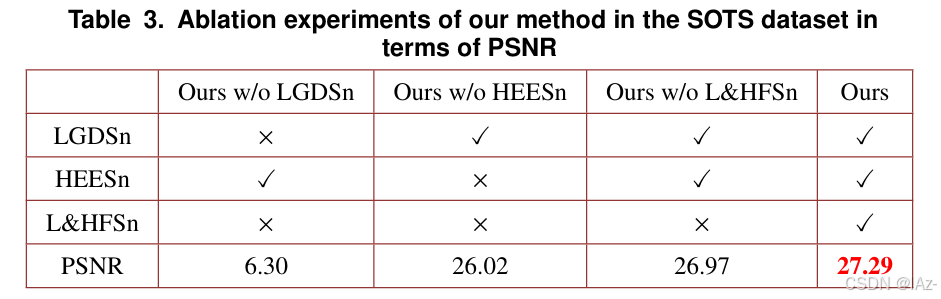
[CR]厚云填补_SEGDNet
Structure-transferring edge-enhanced grid dehazing network Abstract 在过去的二十年里,图像去雾问题在计算机视觉界受到了极大的关注。在雾霾条件下,由于空气中水汽和粉尘颗粒的散射,图像的清晰度严重降低,使得许多计算机视觉…...
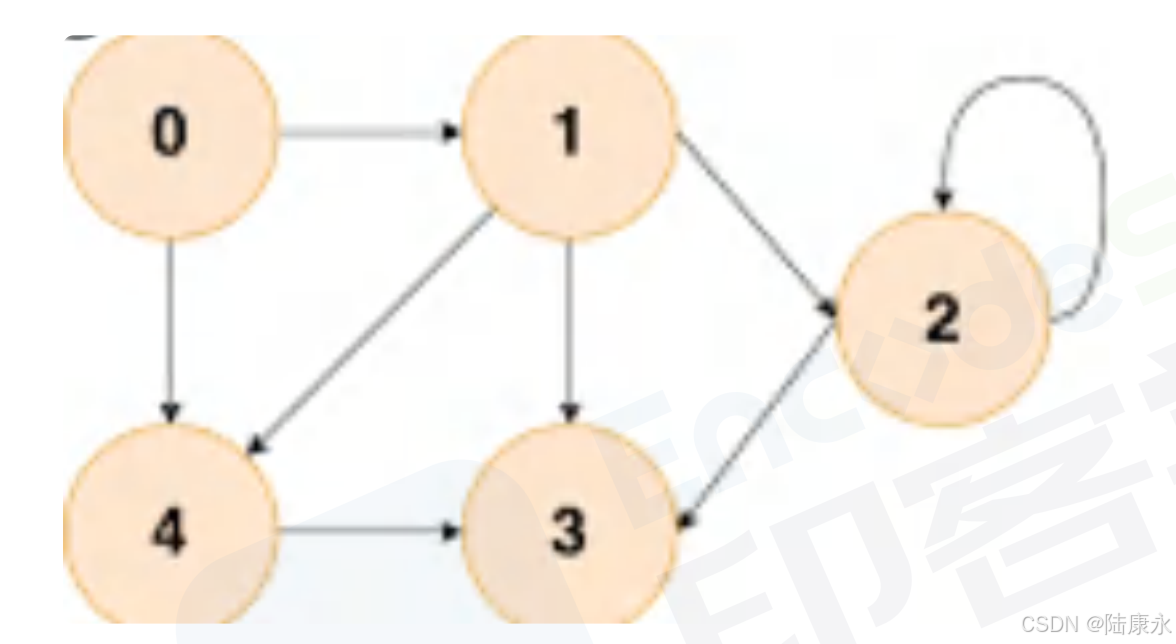
图-基础概念
是什么 图是一种抽象的数据类型,在图中的数据元素通常称作节点,V是所以定点的集合,E是所有边的集合 图的分类 有向图 如果两个订单v,w,只能由v向w,而不能w向v,那么我们就把何种情况叫做一个从…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
