基于FPGA的数字信号处理（22）--进位保存加法器（Carry Save Adder, CSA）

目录

1、拆解多个数的加法

2、进位保存加法器

3、CSA的优点和缺点

4、CSA电路的实现

---

         文章总目录点这里：《基于FPGA的数字信号处理》专栏的导航与说明

---

1、拆解多个数的加法

        考虑3个4bits数相加，10 + 4 + 7 = 21 的过程是这样的：

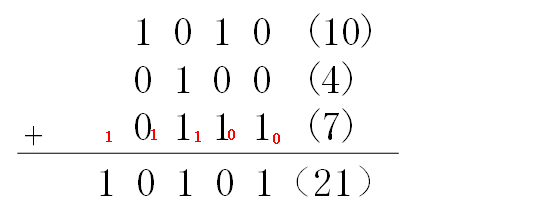
        其中的红色数字是由低位向高位产生的进位，因为进位值是直接在当前位与3个加数相加，所以我们也可以把进位值拆解出来，改写成如下格式：

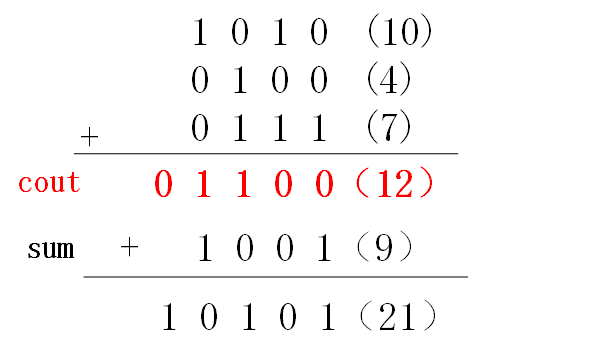
cout是低位产生的进位。例如，最低位的3个值是0/0/1，所以产生了向高位的进位0；次低位的3个值是1/0/1，所以产生了向高位的进位1。

sum是不考虑进位值时3个数相加的和。例如，最低位的3个值是0/0/1，所以该位的和为1；次低位的3个值是1/0/1，所以该位的和为0。

        这样分别产生了进位cout = 01100，和sum=1001，二者相加后的结果就是最终3个数的和即21。这种方法相当于把3个数的加法转换成了2个数的加法。

2、进位保存加法器

        上面这种将3个数的加法转换成两个数加法形式的电路就叫做 进位保存加法器（Carry Save Adder, CSA）。

        当3个数中有2个或3个1时就会向高位产生进位，而和的值则和1的个数相关，奇数个1时和为1，偶数个1时和为0，所以它的真值表如下：

加数1	加数2	加数3	结果	进位
a	b	c	sum	cout
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

        如果你仔细点观察，就会发现上面的真值表和全加器FA的真值表是一样的，这不就说明CSA就是FA吗？只是FA的进位输入都改成了第3个加数，如下：

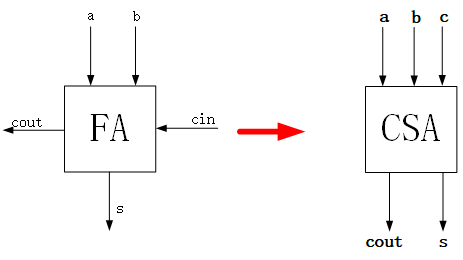
        对于3个4bits的加法，就可以用4个CSA来组成：

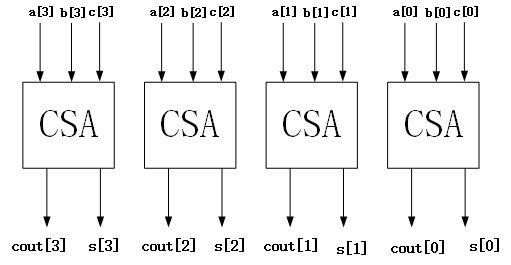
        可以看到这样结构的加法器的关键路径的延迟是多少呢？一个CSA电路的延迟，也就是一个FA的延迟，如下（3个门电路）：

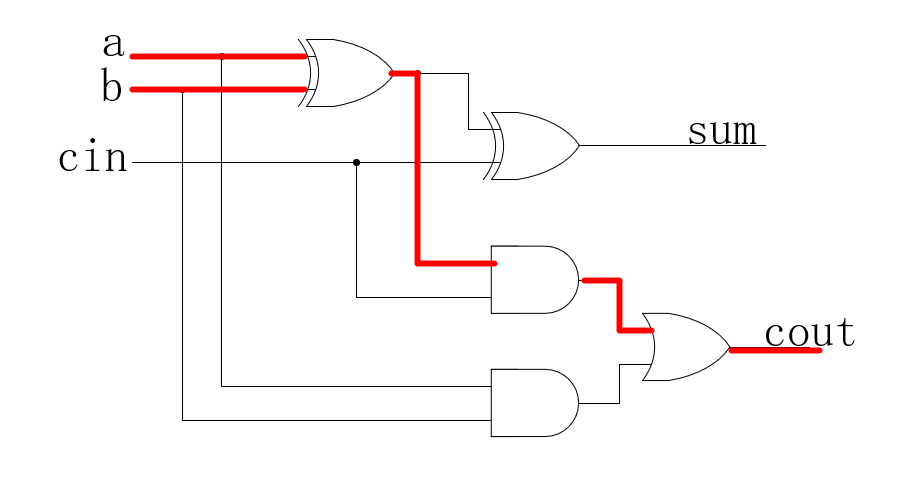
3、CSA的优点和缺点

        上面说了3个数的加法，如果使用CSA电路，那么关键路径的延迟只有3个门电路，而如果使用常规的RCA（行波进位加法器）呢？考虑6个4bits数相加，其一般的电路结构如下：

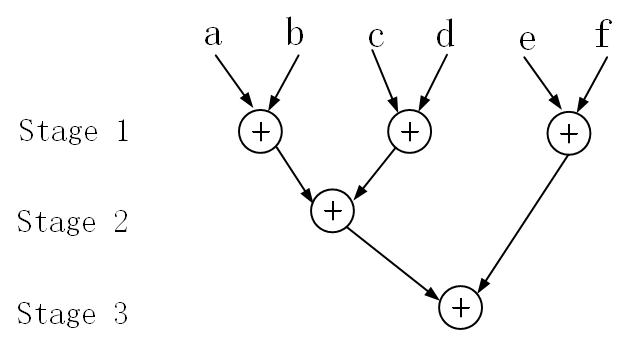
        如果其中的加法器是RCA，那么该电路的关键路径延迟是3级加法器的延迟。如果采用CSA电路，则其电路结构如下：

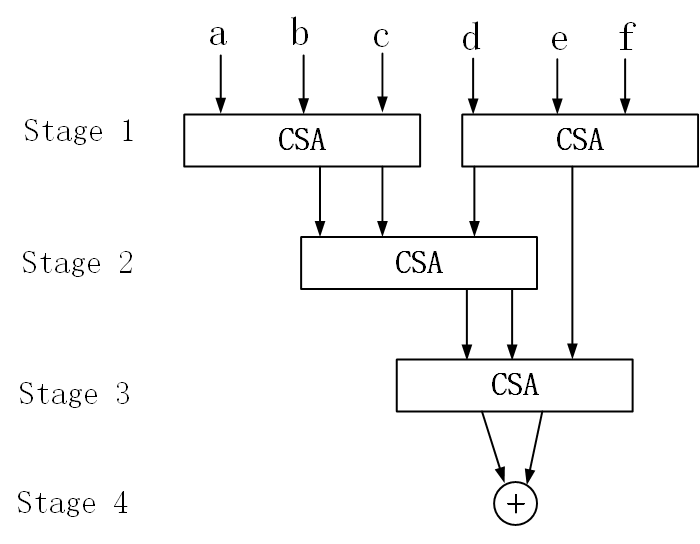
        前面说了，CSA电路的延迟也就一个门电路，那么上面电路的关键路径延迟就是 3个门电路 + 最后的加法器 的延迟，假设加法器也是使用的RCA加法器，那么最终的延迟就是 1个RCA的延迟 + 3个门电路 延迟，这显然比3级RCA电路的延迟要小。可以预见的是，随着加数个数的增加，两种电路的延迟差距还会拉大。

        以4比特乘法为例，其竖式计算表示如下：

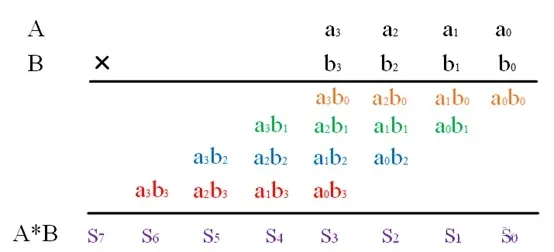
        ai和bi分别表示A和B的某个bit，aibi表示ai与bi相与，使用与门电路生成，aibi的值只有0和1。S表示AB相乘的结果。每一列使用半加器HA或全加器FA两两相加，其结果表示为Si，每一列每两个数产生的进位将传递至相邻高的一列参与计算。其电路结构如下（其中虚线箭头表示进位传播的路线）：

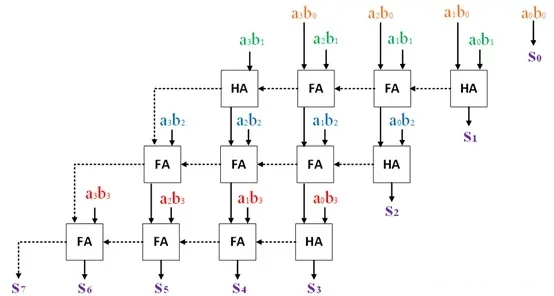
        根据进位传播链，可以看出该电路的关键路径如下：

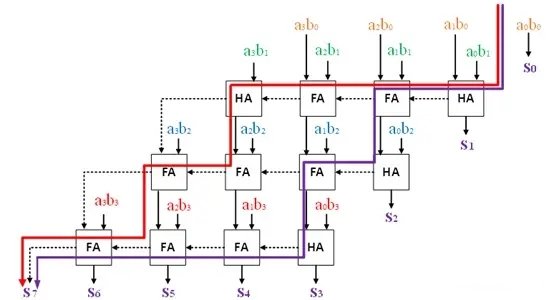
        红线和紫线是由于累加造成的进位链的最长路径。其中：

• 红色路径：6个FA + 2个HA

• 紫色路径：5个FA + 3个HA

        使用进位保留加法器CSA可缩短该进位链的传播延时，其电路结构如下：

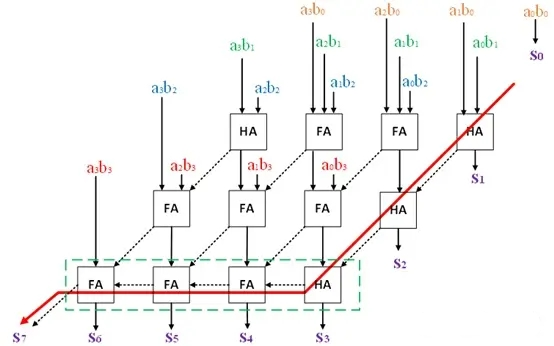
        将RCA阵列乘法器的进位连接至斜下角的加法器，CSA结构的阵列乘法器将进位与和分别计算，不必计算该层的进位，省去了行波进位加法器进位链的依赖，只在最后一级通过RCA结构（上图绿色虚框）传递进位合并最后的结果。上图红色是CSA结构的关键路径：3个FA + 3个HA。可见，CSA结构使用相同的资源却有更优的时序性能，当加法个数变多时，这一优势将更大。

        进位保存加法器的优点如下：

• 进位保存加法器将 3 个数字的加法减少到 2 个数字

• 由于进位传播级很少，与其他类型的加法器相比，它的功耗较低

• 该加法器可以一次执行三位加法

• 无论最终操作完成，下一级都会使用简单的 N 位 RCA。

        进位保存加法器的缺点如下：

• 在进位保存加法的每一步中，可以立即知道加法结果，但我们不知道加法结果与给定数字相比是更小还是更大。

• 这种类型的加法器不能解决将 2 个整数相加以生成单个输出的问题。相反，它只是将 3 个整数相加并生成两个整数，因此两个整数的总和等于三个输入的总和。

• 它对于少数位操作具有高功耗和传播延迟。

4、CSA电路的实现

        接下来，以6个8bits有符号数的加法为例，看如何用CSA的树形结构实现。首先要确定的是，对于单个bit的CSA来说，就是全加器，如下：

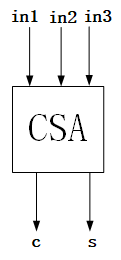
        所以它的生成公式是：

s = in1 ^ in2 ^ in3; c = (in1&in2) | (in1&in3) | (in2&in2) ;

        第1级有2个CSA电路，它们实现3个8bits的加法。第1个CSA的输入是3个加数a,b,c，输出是8bit的和csa11_s 跟 进位csa11_c，需要注意的是进位csa11_c在参与下级加法的时候要左移1bit（即乘2），因为它是向高位的进位。代码如下：

//第1级的第1个 CSA
assign csa11_in1 = a;
assign csa11_in2 = b;
assign csa11_in3 = c;
assign csa11_s = csa11_in1 ^ csa11_in2 ^ csa11_in3;
assign csa11_c = (csa11_in1 & csa11_in2) | (csa11_in1 & csa11_in3) | (csa11_in2 & csa11_in3);

        第2个CSA的输入是3个加数d,e,f，输出是8bit的和csa12_s 跟 进位csa12_c，需要注意的是进位csa12_c在参与下级加法的时候要左移1bit（即乘2），因为它是向高位的进位。代码如下：

//第1级的第2个 CSA
assign csa12_in1 = d;
assign csa12_in2 = e;
assign csa12_in3 = f;
assign csa12_s = csa12_in1 ^ csa12_in2 ^ csa12_in3;
assign csa12_c = (csa12_in1 & csa12_in2) | (csa12_in1 & csa12_in3) | (csa12_in2 & csa12_in3);

        第2级只有1个CSA，它的输入是第1级第1个CSA的两个输出和第2个CSA的一个输出，因为输入中有两个数是上级CSA产生的进位，所以需要左移1位，这样原本的8bits加法就变成了9bits加法。输出是9bit的和csa21_s 跟 进位csa21_c，需要注意的是进位csa21_c在参与下级加法的时候要左移1bit（即乘2），因为它是向高位的进位。代码如下：

//第2级的CSA
assign csa21_in1 = {csa11_c,1'b0};          //左移1比特
assign csa21_in2 = {csa11_s[7],csa11_s};    //为了适配csa21_in1，在高位补符号位
assign csa21_in3 = {csa12_s[7],csa12_s};    //为了适配csa21_in1，在高位补符号位
assign csa21_s = csa21_in1 ^ csa21_in2 ^ csa21_in3;
assign csa21_c = (csa21_in1 & csa21_in2) | (csa21_in1 & csa21_in3) | (csa21_in2 & csa21_in3);

        第3级只有1个CSA，它的输入是第2级的CSA的两个输出和第1级的第2个CSA的一个输出，因为输入中有1个数是上级CSA产生的进位，所以需要左移1位，这样原本的9bits加法就变成了10bits加法。输出是10bit的和csa31_s 跟 进位csa31_c，需要注意的是进位csa31_c在参与下级加法的时候要左移1bit（即乘2），因为它是向高位的进位。代码如下：

//第3级的CSA
assign csa31_in1 = {csa21_c,1'b0};                  //左移1比特
assign csa31_in2 = {csa21_s[8],csa21_s};            //为了适配csa31_in1，在高位补符号位
assign csa31_in3 = {csa12_c[7],csa12_c,1'b0};       //左移1bit，在高位补符号位
assign csa31_s = csa31_in1 ^ csa31_in2 ^ csa31_in3;
assign csa31_c = (csa31_in1 & csa31_in2) | (csa31_in1 & csa31_in3) | (csa31_in2 & csa31_in3);

        经过3级CSA产生的 和csa31_s 跟 进位csa31_c就是6个数相加的结果，但是它不是一个直接表示的数值，而是拆成了两部分的冗余结果，所以我们还需要设计一个加法，来将这两个数相加，这样得到的结果最是最终的6个数的加法结果。这里仍然要注意，进位需要左移1bit（乘2），如下：

//第4级加法-------------------------------------------------------------------------------------
//把 和 + 进位，得到最终的加法结果。因为进位要左移1位,所以和也要在高位补符号位
assign sum = {csa31_c,1'b0} + {csa31_s[9],csa31_s};

        综上，总体的RTL代码如下：

//CSA的生成公式：
//  s = in1 ^ in2 ^ in3;
//  c = (in1&in2)  | (in1&in3)  | (in2&in3) ;
module csa(input   [7 :0]  a,b,c,d,e,f,output  [10:0]  sum_1
);
//----------------------------------------------------------
//定义有关wire
wire [7:0]  csa11_in1,csa11_in2,csa11_in3;
wire [7:0]  csa12_in1,csa12_in2,csa12_in3;
wire [7:0]  csa11_s,csa11_c;
wire [7:0]  csa12_s,csa12_c;
​
//第1级的第1个 CSA
assign csa11_in1 = a;
assign csa11_in2 = b;
assign csa11_in3 = c;
assign csa11_s = csa11_in1 ^ csa11_in2 ^ csa11_in3;
assign csa11_c = (csa11_in1 & csa11_in2) | (csa11_in1 & csa11_in3) | (csa11_in2 & csa11_in3);
​
//第1级的第2个 CSA
assign csa12_in1 = d;
assign csa12_in2 = e;
assign csa12_in3 = f;
assign csa12_s = csa12_in1 ^ csa12_in2 ^ csa12_in3;
assign csa12_c = (csa12_in1 & csa12_in2) | (csa12_in1 & csa12_in3) | (csa12_in2 & csa12_in3);
​
//第2级-------------------------------------------------------------------------------------
//定义有关wire,因为上级的进位是往高位进位，所以需要左移1比特，即cout是9bits,
//为了适配，其他输入也要在高位补符号位到9bits
wire [8:0]  csa21_in1,csa21_in2,csa21_in3;
wire [8:0]  csa21_s,csa21_c;
​
//第2级的CSA
assign csa21_in1 = {csa11_c,1'b0};          //左移1比特
assign csa21_in2 = {csa11_s[7],csa11_s};    //为了适配csa21_in1，在高位补符号位
assign csa21_in3 = {csa12_s[7],csa12_s};    //为了适配csa21_in1，在高位补符号位
assign csa21_s = csa21_in1 ^ csa21_in2 ^ csa21_in3;
assign csa21_c = (csa21_in1 & csa21_in2) | (csa21_in1 & csa21_in3) | (csa21_in2 & csa21_in3);
​
//第3级-------------------------------------------------------------------------------------
//定义有关wire,因为上级的进位是往高位进位，所以需要左移1比特，即cout是10bits,
//为了适配，其他输入也要在高位补符号位到10bits
wire [9:0]  csa31_in1,csa31_in2,csa31_in3;
wire [9:0]  csa31_s,csa31_c;
​
//第3级的CSA
assign csa31_in1 = {csa21_c,1'b0};                  //左移1比特
assign csa31_in2 = {csa21_s[8],csa21_s};            //为了适配csa31_in1，在高位补符号位
assign csa31_in3 = {csa12_c[7],csa12_c,1'b0};       //左移1bit，在高位补符号位
assign csa31_s = csa31_in1 ^ csa31_in2 ^ csa31_in3;
assign csa31_c = (csa31_in1 & csa31_in2) | (csa31_in1 & csa31_in3) | (csa31_in2 & csa31_in3);
​
//第4级加法-------------------------------------------------------------------------------------
//把 和 + 进位，得到最终的加法结果。因为进位要左移1位,所以和也要在高位补符号位
assign sum_1 = {csa31_c,1'b0} + {csa31_s[9],csa31_s};
​
endmodule

        接下来写个TB测试一下电路，因为可能的输入太多了，一共有(2^8)^6 = 2^48 = 281,474,976,710,656种情况，显然不可能遍历完，所以我们采用随机测试的方式。通过生成数组随机向量来对电路进行测试：

module tb_test();reg signed  [7 :0]  a,b,c,d,e,f;
wire        [10:0]  sum;
wire                sum_flag;               //结果比对正确时拉高
​
wire signed [10:0] sum_real;
​
assign sum_real = a + b + c + d + e + f;    //预期的正确结果
assign sum_flag = sum == sum_real;          //判断电路输出是否与预期输出一致
​
initial begin//赋初值a = 0;b = 0;c = 0;d = 0;e = 0;f = 0;#5;repeat(1024)begin   //设定向量个数//生成随机向量a = $random();b = $random();c = $random();d = $random();      e = $random();      f = $random();      #5;end#10 $stop();    //结束仿真
end//例化被测试模块   
csa u_csa(.a      (a      ),.b      (b      ),.c      (c      ),.d      (d      ),.e      (e      ),.f      (f      ),  .sum    (sum    )
);
​
endmodule

        加法运算的预期结果也是很容易就可以找出来的，就是在TB中直接写加法就行。接着构建了向量sum_flag作为电路输出与预期结果的对比值，当二者一致时即拉高这两个信号。这样我们只要观察这个信号，即可知道电路输出是否正确。仿真结果如下：

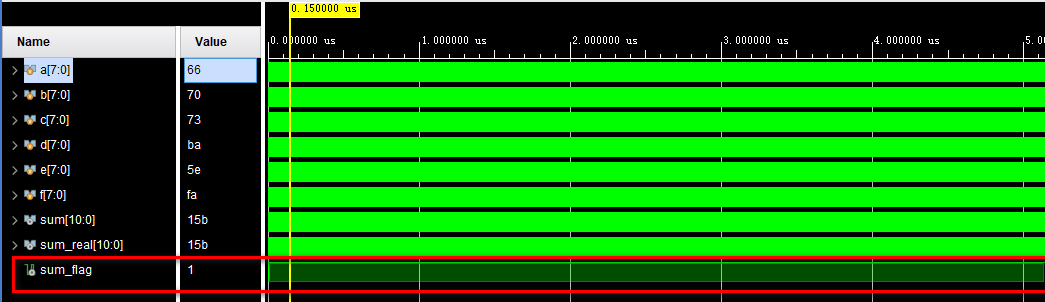
        可以看到，sum_flag都是一直拉高的，说明电路输出正确。