二分+dp,CF 1993D - Med-imize
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
| D - Med-imize |
二、解题报告
1、思路分析
对于n <= k的情况直接排序就行
对于n > k的情况
最终的序列长度一定是 (n - 1) % k + 1
这个序列是原数组的一个子序列
对于该序列的第一个元素,其下标 mod k 一定为0
为什么呢?
不为0,则第一个元素前面的元素不能删除干净
那么,为了让剩下的元素都能合法的拿进来,两两元素之间的距离应为k的倍数
继而推出,剩余序列在原数组的下标mod k 为[0, k - 1]
那么原数组中的元素要么不能拿进最终序列,要么在最终序列中的位置是确定的
我们记可拿进最终序列的数的集合为S
现在由于要求最终中位数的最大值,我们假设最终中位数为x
我们发现x越大,S中比x大的数目越少,具有单调性,于是就可以二分了
如何check?
利用线性dp,判断长度为(n - 1) % k + 1的最终序列中最多有多少个数 >= x
假如最终结果是cnt,那么只要cnt * 2 > (n - 1) % k + 1,说明可能还能更大,我们就收缩左边界
否则收缩右边界
本题要点:分析出最终序列原数组下标mod k 的特点,以及中位数的单调性
2、复杂度
时间复杂度: O(NlogN)空间复杂度:O(N)
3、代码详解
#include <bits/stdc++.h>
#include <ranges>
// #define DEBUG
using i64 = long long;
using u32 = unsigned;
using u64 = unsigned long long;
constexpr int inf32 = 1E9 + 7;
constexpr i64 inf64 = 1E18 + 7;
constexpr double eps = 1e-9;void solve() {int n, k;std::cin >> n >> k;std::vector<int> a(n);for (int i = 0; i < n; ++ i) {std::cin >> a[i]; }if (n <= k) {std::sort(a.begin(), a.end());std::cout << a[(n - 1) / 2] << '\n';return;}int sz = n % k;if (!sz) sz = k;auto check = [&](int x)-> bool {std::vector<int> f(sz, -inf32);for (int i = 0; i < n; ++ i) {int j = i % k;if (j >= sz) continue;f[j] = std::max(f[j], (j ? f[j - 1] : 0) + (a[i] >= x));}return f.back() * 2 > sz;};std::vector<int> b(a);std::sort(b.begin(), b.end());b.resize(std::unique(b.begin(), b.end()) - b.begin());int lo = 0, hi = b.size();while (hi - lo > 1) {int x = lo + hi >> 1;if (check(b[x]))lo = x;elsehi = x;}std::cout << b[lo] << '\n';
}auto FIO = []{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);return 0;
} ();int main() {#ifdef DEBUGfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);#endif int t = 1;std::cin >> t;while (t --)solve();return 0;
}相关文章:

二分+dp,CF 1993D - Med-imize
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 D - Med-imize 二、解题报告 1、思路分析 对于n < k的情况直接排序就行 对于n > k的情况 最终的序列长度一定是 (n - 1) % k 1 这个序列是原数组的一个子序列 对于该序列的第一个元素࿰…...

三十种未授权访问漏洞复现 合集( 三)
未授权访问漏洞介绍 未授权访问可以理解为需要安全配置或权限认证的地址、授权页面存在缺陷,导致其他用户可以直接访问,从而引发重要权限可被操作、数据库、网站目录等敏感信息泄露。---->目录遍历 目前主要存在未授权访问漏洞的有:NFS服务&a…...
数据湖和数据仓库核心概念与对比
随着近几年数据湖概念的兴起,业界对于数据仓库和数据湖的对比甚至争论就一直不断。有人说数据湖是下一代大数据平台,各大云厂商也在纷纷的提出自己的数据湖解决方案,一些云数仓产品也增加了和数据湖联动的特性。但是数据仓库和数据湖的区别到…...

探索WebKit的奥秘:打造高效、兼容的现代网页应用
1. 简介 1.1. 主要特点 WebKit 是一个开源的浏览器引擎,它允许开发者构建高性能、功能丰富的 web 应用程序。WebKit 与 Mozilla Firefox 等使用的 Gecko 引擎、Internet Explorer 使用的 Trident 引擎以及 EdgeHTML 引擎共同构成了现代 web 浏览器的核心技术。 1.2. 学习资…...

【leetcode】平衡二叉树、对称二叉树、二叉树的层序遍历(广度优先遍历)(详解)
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 🌱🌱个人主页:奋斗的明志 🌱🌱所属专栏:数据结构、LeetCode专栏 📚本系…...

最短路径算法:Floyd-Warshall算法
引言 在图论中,Floyd-Warshall算法是一种用于计算任意两点之间最短路径的动态规划算法。它适用于加权有向图和无向图,可以处理带有负权重边的图,但要求图中不能有负权重环。本文将详细介绍Floyd-Warshall算法的定义、步骤及其实现。 Floyd-…...

3DM游戏运行库合集离线安装包2024最新版
3DM游戏运行库合集离线安装包是一款由国内最大的游戏玩家论坛社区3DM推出的集成式游戏运行库合集软件,旨在解决玩家在玩游戏时遇到的运行库缺失或错误问题。该软件包含多种常用的系统运行库组件,支持32位和64位操作系统,能够自动识别系统版本…...

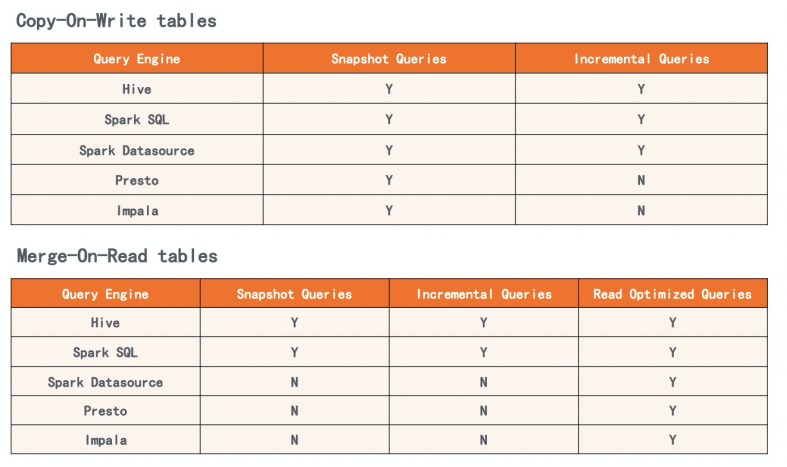
【Bigdata】什么是混合型联机分析处理
这是我父亲 日记里的文字 这是他的生命 留下留下来的散文诗 几十年后 我看着泪流不止 可我的父亲已经 老得像一个影子 🎵 许飞《父亲写的散文诗》 混合型联机分析处理(Hybrid OLAP,简称 HOLAP)是一种结合了多…...

Java 并发编程:volatile 关键字介绍与使用
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 026 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

【Spark计算引擎----第三篇(RDD)---《深入理解 RDD:依赖、Spark 流程、Shuffle 与缓存》】
前言: 💞💞大家好,我是书生♡,本阶段和大家一起分享和探索大数据技术Spark—RDD,本篇文章主要讲述了:RDD的依赖、Spark 流程、Shuffle 与缓存等等。欢迎大家一起探索讨论!࿰…...

四、日志收集loki+ promtail+grafana
一、简介 Loki是受Prometheus启发由Grafana Labs团队开源的水平可扩展,高度可用的多租户日志聚合系统。 开发语言: Google Go。它的设计具有很高的成本效益,并且易于操作。使用标签来作为索引,而不是对全文进行检索,也就是说&…...

xdma的linux驱动编译给arm使用(中断检测-测试程序)
1、驱动链接 XDMA驱动源码官网下载地址为:https://github.com/Xilinx/dma_ip_drivers 下载最新版本的XDMA驱动源码,即master版本,否则其驱动用不了(xdma ip核版本为4.1)。 2、驱动 此部分来源于博客:xd…...

探索之路——初识 Vue Router:构建单页面应用的完整指南
目录 1. Vue Router 简介 2. 安装与配置 Vue Router 安装步骤 配置路由 3. 在 Vue 应用中使用路由 4. 进阶使用 路由守卫 懒加载 高级路由技术 嵌套路由 动态路由匹配 编程式的路由导航 路由懒加载 路由元信息 在现代前端开发中,单页面应用(SPA)因其出…...

传输层_计算机网络
文章目录 运输层UDPTCPTCP连接管理TCP三次握手TCP四次挥手 可靠机制流量控制拥塞控制 QUIC 运输层 网络层提供了主机之间的逻辑通信 运输层为运行在不同主机上的进程之间提供了逻辑通信 UDP(用户数据报协议)提供一种不可靠、无连接的服务,数据报 TCP(传输控制协议)…...
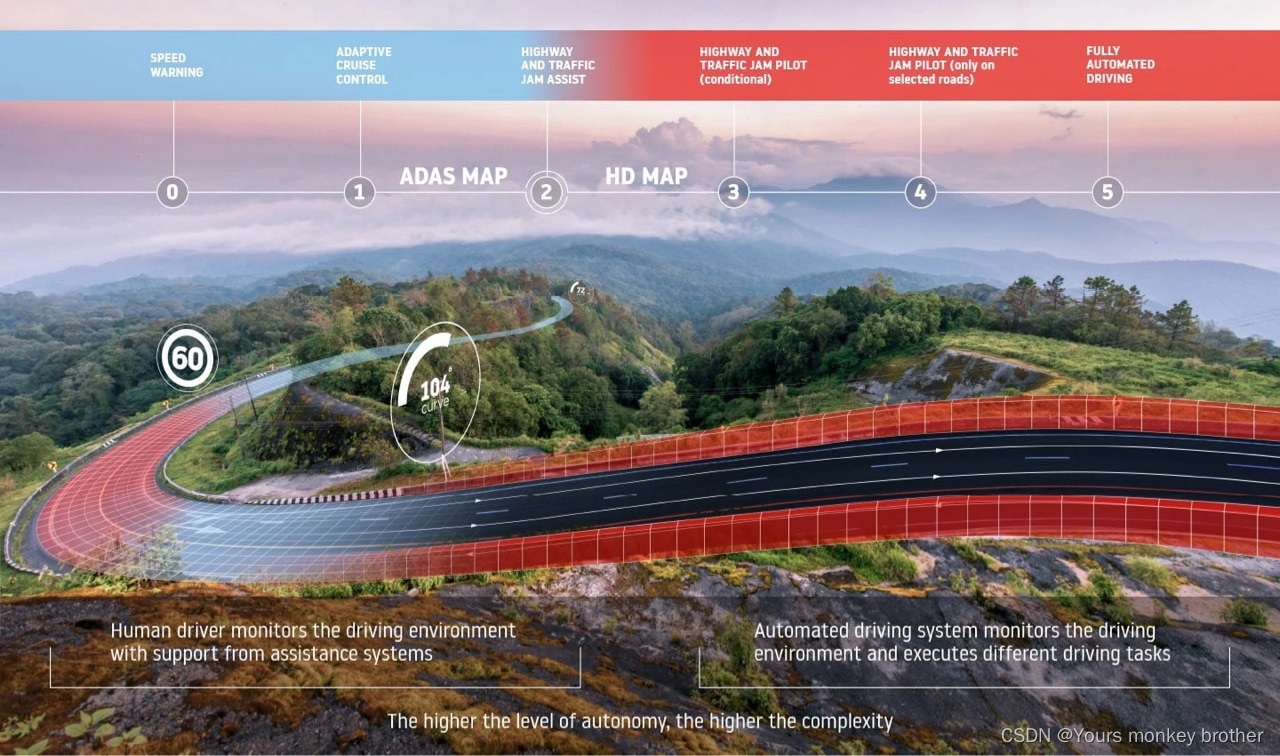
自动驾驶的六个级别是什么?
自动驾驶汽车和先进的驾驶辅助系统(ADAS)预计将帮助拯救全球数百万人的生命,消除拥堵,减少排放,并使我们能够在人而不是汽车周围重建城市。 自动驾驶的世界并不只由一个维度组成。从没有任何自动化到完整的自主体验&a…...

深度学习复盘与论文复现F
文章目录 1、Environment construction1.1 macos conda1.2 macos PyTorch1.3 iTerm settings1.4 install jupyter 2、beam search2.1 greedy search2.2 exhaustive search2.3 beam search 3、Attention score3.1 Masking softmax operation3.2 Additive attention3.3 Zoom dot …...

如何学习自动化测试工具!
要学习和掌握自动化测试工具的使用方法,可以按照以下步骤进行: 一、明确学习目标 首先,需要明确你想要学习哪种自动化测试工具。自动化测试工具种类繁多,包括但不限于Selenium、Appium、JMeter、Postman、Robot Framework等&…...

短信接口被恶意盗刷
短信接口被恶意盗刷是指攻击者通过各种手段,大量发送短信请求,导致短信资源被浪费,服务提供商可能面临经济损失,正常用户的服务也可能受到影响。以下是一些可能导致短信接口被恶意盗刷的原因和相应的解决方案: 原因&a…...

实验4-2-1 求e的近似值
//实验4-2-1 求e的近似值 /* 自然常数 e 可以用级数 11/1!1/2!⋯1/n!⋯ 来近似计算。 本题要求对给定的非负整数 n,求该级数的前 n1 项和。 输入格式:输入第一行中给出非负整数 n(≤1000)。 输出格式:在一行中输出部分和的值,保留…...

内网穿透--LCX+portmap转发实验
实验背景 通过公司带有防火墙功能的路由器接入互联网,然后由于私网IP的缘故,公网 无法直接访问内部web服务器主机,通过内网其它主机做代理,穿透访问内网web 服务器主机 实验设备 1. 路由器、交换机各一台 2. 外网 kali 一台&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...


