MATLAB霍夫曼表盘识别系统
MATLAB霍夫曼表盘识别系统
一、介绍
本设计为基于MATLAB的表盘指针识别,算法原理是基于hough变换。可检测压力表,石英手表,电表刻度,气压表等带指针刻度的表盘。通过hough检测直线和圆的关系,得出指针夹角,根据刻度换算关系得出具体刻度值。算法流程为:原图,灰度变换,二值化,hough变换,刻度指针处刻度定位,计算夹角,得出示数。本设计带有一个人机交互GUI界面,操作人性化,逻辑清晰。
二、运行图

三、核心代码
RGB=imread('14.jpg');
figure,imshow(RGB); title('RGB')
GRAY=rgb2gray(RGB);
figure,imshow(GRAY); title('GRAY')
threshold=graythresh(GRAY);
BW=im2bw(GRAY,threshold);
figure,imshow(BW); title('BW')
BW=~BW;
figure,imshow(BW); title('~BW')
BW=bwmorph(BW,'thin',Inf);
figure,imshow(BW); title('BWMORPH')
[M,N]=size(BW);
[H,T,R] = hough(BW);
figure;
imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');xlabel('\theta'), ylabel('\rho');axis on, axis normal, hold on;P = houghpeaks(H,1,'threshold',ceil(0.3*max(H(:))));x = T(P(:,2));y = R(P(:,1));plot(x,y,'s','color','white');
%%%%%%%%%%%%%%%%%%%% Find lines and plot them%%%%%%%%%%%%%%for k = 1:length(lines)xy = [lines(k).point1; lines(k).point2];plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
%%%%%%%%%% plot beginnings and ends of lines%%%%%%%%%%%%%%%%%%plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow'); plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
%%%% determine the endpoints of the longest line segment %%%%len = norm(lines(k).point1 - lines(k).point2);if ( len > max_len)max_len = len;xy_long = xy;endend
%%%%%%%%%%%%% highlight the longest line segment%%%%%%%%%%%%%%plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','cyan');k=(xy(2,2)-xy(1,2))/(xy(2,1)-xy(1,1));theta=pi/2+atan(k);if((xy(1,1)+xy(2,1))/2<=N/2)q=(theta+pi)*180/3.14; elseq=theta*180/3.14; endshishu=q*6/2700-0.2;disp (theta);disp (q);disp (shishu);
相关文章:

MATLAB霍夫曼表盘识别系统
MATLAB霍夫曼表盘识别系统 一、介绍 本设计为基于MATLAB的表盘指针识别,算法原理是基于hough变换。可检测压力表,石英手表,电表刻度,气压表等带指针刻度的表盘。通过hough检测直线和圆的关系,得出指针夹角࿰…...

Python | Leetcode Python题解之第322题零钱兑换
题目: 题解: class Solution:def coinChange(self, coins: List[int], amount: int) -> int:dp [float(inf)] * (amount 1)dp[0] 0for coin in coins:for x in range(coin, amount 1):dp[x] min(dp[x], dp[x - coin] 1)return dp[amount] if d…...

python中类class的魔法方法
开始介绍之前,我们先看下之前文章我们介绍过的内置类merryview的一些方法,如下图所示: 有很多双下划线开始和结束的method,这么多method是做啥子用的呢? 其实这些方法就是我们常说的魔法方法,也是python中的…...

计算机体系结构和计算机组成原理的区别
如何理解计算机体系结构和计算机的组成?哪个对计算机的性能更重要?说明理由 目录 计算机体系结构 计算机组成 二者区别 哪个对性能更重要 计算机体系结构 计算机体系结构是指根据属性和功能不同而划分的计算机理论组成部分及计算机基本工作原理、理论…...

MySQL--数据库备份
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 一、为什么要备份 备份:能够防止由于机械故障以及人为误操作带来的数据丢失,例如将数据库文件保存在了其它地方。 冗余&#…...

influxDB的常用命令
目录 1.查看数据库命令 2.进入某数据库命令 3.创建表的命令 (host 和region 字段是必须的) 4.显示所有的表命令 5. 删除表 6.查询表数据 7.显示数据库用户 8.创建用户 9.创建管理员用户 10.修改密码(密码用单引号括住,不要用双引号) 11. 分配数据库访问权…...

使用 1panel面板 部署 springboot 和 vue
代码仓库:还没弄 目录 网站介绍安装步骤1. 准备云服务器2. 准备域名(可跳过)3. 安装1panel面板4. 服务器开放端口5. 进入1panel面板6. 安装并启动软件(服务器和面板开放端口)7. 打包并上传项目7.1 打包 Java项目&#…...

快速体验LLaMA-Factory 私有化部署和高效微调Llama3模型(曙光超算互联网平台异构加速卡DCU)
序言 本文以 LLaMA-Factory 为例,在超算互联网平台SCNet上使用异构加速卡AI 显存64GB PCIE,私有化部署Llama3模型,并对 Llama3-8B-Instruct 模型进行 LoRA 微调、推理和合并。 快速体验基础版本,请参考另一篇博客:快…...

Cocos Creator 3.8.x bundle设置最佳方案
A: 项目开始场景(Start Scene)加载显示最快的Bundle设置方案:不要使用resources文件夹,除了项目开始场景(Start Scene)所在文件夹,将所有文件分类设置成Bundle; B: A方案较为麻烦,项目文件夹多时…...

【论文笔记】4D Millimeter-Wave Radar in Autonomous Driving: A Survey
原文链接:https://arxiv.org/abs/2306.04242 I. 引言 传统毫米波雷达(3D毫米波雷达)测量俯仰角的能力有限,数据通常仅包括距离、水平角和多普勒速度信息。此外,3D雷达数据存在噪声且分辨率低(尤其是水平角…...
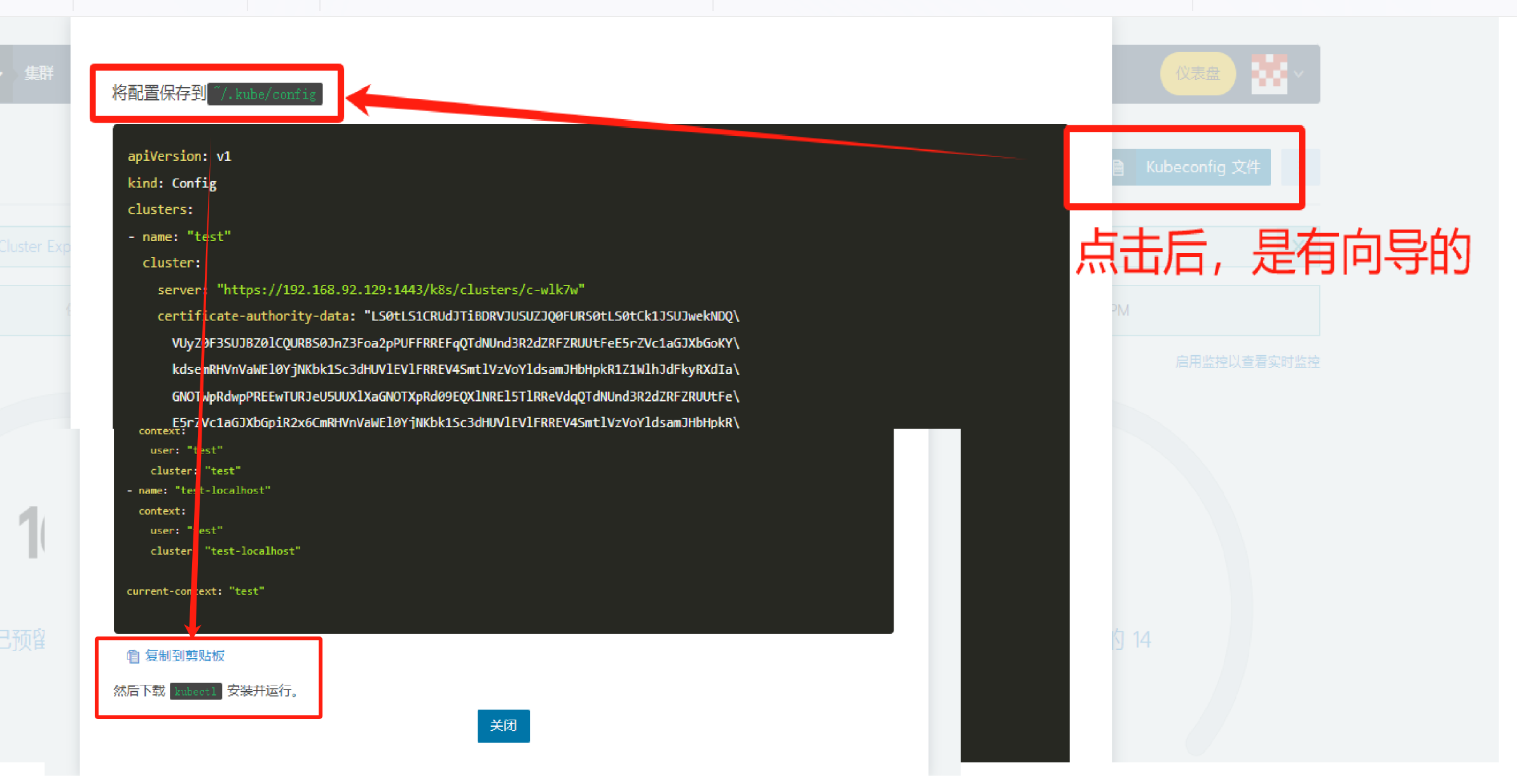
搭建 Rancher 服务,配置k8s集群
1. 前提条件 前提条件: 安装docker,要求版本各节点版本一致。网上还有额外的要求:关闭swap、禁用selinux等等。 2. 搭建 Rancher 服务 直接通过docker命令实现即可,很方便。 docker run -d \--name rancher \--restart unles…...

数据恢复的定制之旅:打造SQL Server的专属恢复方案
数据恢复的定制之旅:打造SQL Server的专属恢复方案 在企业运营中,数据的安全性和可靠性是至关重要的。SQL Server作为企业级数据库解决方案,提供了多种数据恢复技术以应对不同的数据丢失场景。然而,面对特定的业务需求和复杂的数…...

Javascript常见算法详解
在JavaScript(JS)中,常见的算法涵盖了多个领域,从基础的数组操作到更复杂的排序、搜索和数据结构算法。下面是一些在JS中常见的算法示例: 1. 排序算法 Java排序算法-CSDN博客 冒泡排序(Bubble Sort&#x…...

MySQL数据管理 - 查询语句
文章目录 查询数据1 查询指定列2 条件查询3 合并查询4 模糊查询5 聚合函数查询6 对值进行排序7 分组查询8 分页查询9 数据库关联查询1 内连接 INNER JOIN2 LEFT JOIN3 右连接 10 数据库子查询参考 查询数据 数据库最常用的操作就是查询,也是数据操作的基础…...

经典图论算法回顾之Bellman-Ford算法
Dijkstra最短路径算法存在的一个问题是不能处理负权图(详见:经典图论算法回顾之Dijkstra算法。今天要回顾的Bellman-Ford算法(wikipedia:Bellman–Ford algorithm)可以求出有负权图的最短路径,并可以对最短…...

LinuxC++(10):调用可执行程序
认识system函数 可以直接用system在代码中实现调用shell命令 /bin/ls -l /tmp表示执行ls -l命令,打开/tmp地址 而前面的/bin/表示这是shell命令,不可少,可以认为,/bin/后面的就是等价于shell里面输入的命令。 然后,cou…...

C语言指针·高级用法超详解(指针运算、野指针、悬空指针、void类型指针、二级以及多级指针)
目录 1. 指针的运算 2. 野指针和悬空指针 2.1 野指针 2.2 悬空指针 3. void类型指针 4. 二级指针和多级指针 4.1 命名规则 4.2 作用 4.2.1 二级指针可以操作一级指针记录的地址 4.2.2 利用二级指针获取变量中记录的数据 1. 指针的运算 文章开始前可以先了…...

SQL注入:MySQL元数据库,外网实战手工SQL注入
MySQL元数据库 MySQL的元数据库是一组特殊的数据库,用于存储MySQL服务器的元数据信息,在sql注入中较为常用为以下两种元数据库: information_schema:这个数据库包含了MySQL服务器上所有其他数据库的元数据信息。例如数据库名、表…...

接口与抽象类有什么区别
接口:只能包含抽象方法,成员变量只能是public static final 类型 是对行为的抽象 先约定再接口再实现 抽象类:包含成员变量和一般方法和抽象方法,当继承时,子类必须实现抽象类中的抽象方法...

【时时三省】unity test 测试框架 使用 code blocks 移植(核心文件:unity.c, unity_fixture.c)
山不在高,有仙则名。水不在深,有龙则灵。 ----CSDN 时时三省 目录 1,移植介绍 2,使用 Code::Blocks 17.12 创建工程 3,搬移文件入工程目录 4,更改代码 5,向工程添加文件 6,运…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
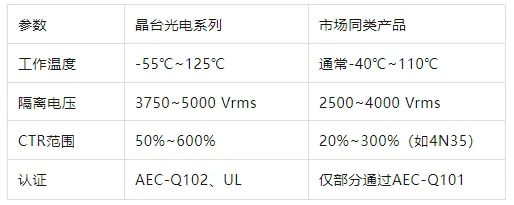
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...
