代码随想录算法训练营第二十天|235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点
写在前边的话
235. 二叉搜索树的最近公共祖先
题目链接
力扣题目链接
题目难度
中等
看到题目的第一想法
看到题目的第一想法,除了昨天做过的普通二叉树的最近祖先的解法利用回溯从底向上搜索,我会想到使用迭代法,但我好像不太会使用到二叉树搜索树的特性,我是选择的层序遍历。得转换下思维了。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if not root:return rootqueue = collections.deque([root])while queue:n = len(queue)for i in range(n):node = queue.popleft()if min(p.val, q.val) <= node.val <= max(p.val, q.val):return nodeif node.left:queue.append(node.left)if node.right:queue.append(node.right)return None
看完代码随想录的总结
文章讲解
代码随想录文章讲解
视频讲解
代码随想录视频讲解
解题思路
1. 递归法:由于没有中节点的逻辑所以前中后序都是可以的。
递归三步曲:
1)入参:根节点,p,q;返回值:满足条件的二叉树节点。
2)终止条件:节点空返回空
3)单次递归逻辑:如果节点小于p,q那么就向右子树遍历;如果节点值大 于p,q那么就向左子树遍历;否则就返回当前节点。
2. 迭代法
从根节点开始遍历,如果当前节点小于p,q那么就向右子树搜索;如果当前节点值大于p,q那么就像左子树搜索;否则返回当前节点。
代码编写
python
# 递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if not root:return rootprint(root.val)if root.val < p.val and root.val < q.val:right_res = self.lowestCommonAncestor(root.right, p, q)if right_res:return right_resif root.val > p.val and root.val > q.val:left_res = self.lowestCommonAncestor(root.left, p, q)if left_res:return left_resreturn root#********************************************************************************# 迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':cur = rootwhile cur:if cur.val < p.val and cur.val < q.val:cur = cur.rightelif cur.val > p.val and cur.val > q.val:cur = cur.leftelse:return curreturn Nonejava
701.二叉搜索树中的插入操作
题目链接
力扣题目链接
题目难度
中等
看到题目的第一想法
看到题目的第一想法是想用迭代法,在遍历节点的时候找到要插入的位置。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:node = TreeNode(val)if not root:return nodecur = rootwhile True:if val < cur.val:print(cur.val)if not cur.left: cur.left = nodereturn rootelse:cur = cur.leftif val > cur.val:if not cur.right:node = TreeNode(val)cur.right = nodereturn rootelse:cur = cur.right看完代码随想录的总结
文章讲解
代码随想录文章讲解
视频讲解
代码随想录视频讲解
解题思路
1.递归法:需要记录父节点(方案一:可以通过递归函数的返回值完成父子节点的赋值这种方法比较便利,方案二:另外也可以找到要插入父节点位置以后再判断是插入到左节点还是右节点)
递归三步曲方案一:
入参:当前节点以及要比较的数值,返回值要插入的节点。
终止条件:节点空则返回要插入的节点。
单次递归逻辑:赋值当前节点给父节点;如果节点值大于要比较的值,那么向左子树遍历;如果当前节点值小于要比较的值,那么向右子树遍历。注意这里返回值会赋值给左右子节点。
递归三步曲方案二:
入参:当前节点以及要比较的数值,无返回值。
终止条件:节点空即下层左节点或者右节点为空了,这个时候由于递归函数没有返回值,所以需要检查比较值是大于父节点还是小于父节点,小于插入到左节点,大于插入到右节点。
单次递归逻辑:赋值当前节点给父节点;如果节点值大于要比较的值,那么向左子树遍历;如果当前节点值小于要比较的值,那么向右子树遍历。
代码编写
python
#方案一
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def __init__(self):self.parent = Nonedef reversal(self, cur, val):if not cur:node = TreeNode(val)return nodeif cur.val > val:cur.left = self.reversal(cur.left, val)else:cur.right = self.reversal(cur.right, val)return cur # 注意这里要一层一层返回最终返回的就是根节点了def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if not root:return TreeNode(val)cur = rootreturn self.reversal(cur, val)#********************************************************************# 方案二
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def __init__(self):self.parent = Nonedef reversal(self, cur, val):if not cur:node = TreeNode(val)if self.parent.val > val:self.parent.left = nodeelse:self.parent.right = nodereturnself.parent = curif cur.val > val:self.reversal(cur.left, val)else:self.reversal(cur.right, val)def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if not root:return TreeNode(val)cur = rootself.reversal(cur, val)return root# ***********************************************************************# 迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:node = TreeNode(val)if not root:return TreeNode(val)cur = rootwhile cur:parent = curif cur.val > val:cur = cur.leftelse:cur = cur.rightif parent.val > val:parent.left = nodeelse:parent.right = nodereturn rootjava
450.删除二叉搜索树中的节点
题目链接
力扣题目链接
题目难度
中等
看到题目的第一想法
没接触过,看到就觉得有点难!
看完代码随想录的总结
文章讲解
代码随想录文字讲解
视频讲解
代码随想录视频讲解
解题思路
1. 递归法(关键单层递归中的情况梳理)
递归三步曲:
1)入参:根节点和要比较的值;返回值:删除节点以后要返回的节点(用于上一层递归来赋值)。
2)终止条件:有五种情况:第一种:节点空则返回空,说明没找到要删除的节点;第二种:遍历到的要删除的节点此时左右节点均为空,那么直接返回空;第三种:遍历到要删除的节点此时左节点不为空右节点为空,那么直接返回左节点;第四种情况:遍历到要删除的节点此时左节点空右节点不为空,那么直接返回右节点;第五种:遍历到要删除的节点了此时左右子节点都不为空,此时需要把左子树放到右子树当中(将删除节点的左子树头结点放到删除节点的右子树的最左面节点的左孩子上),整个时候就成了左节点空右节点非空的情况,返回右节点。
3)单层递归逻辑:遍历左子树,遍历右子树,如果不满足上边终止条件则返回当前节点。
代码编写
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def reversal(self, root, key):if not root:return rootif root.val == key:if not root.left and not root.right:return Noneelif root.left and not root.right:return root.leftelif not root.left and root.right:return root.rightelse:cur = root.rightwhile(cur.left):cur = cur.leftcur.left = root.leftreturn root.rightif root.val > key:root.left = self.reversal(root.left, key)else:root.right = self.reversal(root.right, key)return rootdef deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:return self.reversal(root, key)java
今日总结
今天的题目也都是二叉搜索树的题目,做二叉搜索树的题目,还是要注意利用其特性。在删除和插入二叉树节点的时候使用递归,可以利用返回值进行节点赋值的操作,这样比较简单不用重复去判断条件。
相关文章:

代码随想录算法训练营第二十天|235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点
写在前边的话 235. 二叉搜索树的最近公共祖先 题目链接 力扣题目链接 题目难度 中等 看到题目的第一想法 看到题目的第一想法,除了昨天做过的普通二叉树的最近祖先的解法利用回溯从底向上搜索,我会想到使用迭代法,但我好像不太会使用到二…...

视频美颜SDK与直播美颜插件在实时视频中的应用
视频美颜技术作为提升视频质量的重要手段,已经成为了许多视频和直播应用中不可或缺的一部分。本篇文章,笔者将探讨视频美颜SDK与直播美颜插件在实时视频中的应用,并分析其在用户体验和技术实现方面的重要性。 一、视频美颜SDK的应用场景 视…...

【Linux】yum(工具篇)
文章目录 前言:什么是软件包yum 的介绍yum源yum源的配置第三方源的配置官方源的配置镜像站点安装wget包备份本地yum源配置网易yum源重新生成yum缓存 前言:什么是软件包 在Linux下安装软件, 一个通常的办法是下载到程序的源代码, 并进行编译, 得到可执行程…...

3GPP入门
官网地址 3GPP – The Mobile Broadband Standard 协议下载链接 Directory Listing /ftp/specs/archive 总纲 重点series Signalling protocols ("stage 3") - user equipment to network24 series信令Radio aspects25 series3G 基础LTE (Evolved UTRA), LTE-Adva…...
FFmpeg内存对齐简述
目录 引文 行字节数的计算 ffmpeg中的align ffmpeg中的linesize 内容参考 引文 在ffmpeg的使用过程中有时会发现align这个参数,那么这个参数代表什么意思,不同的值会产生什么影响呢,详见下文。 行字节数的计算 理解内存对齐之前首先要…...
)
手机号码归属地查询接口如何对接?(一)
一、什么是手机号码归属地接口? 通过手机号查询归属地信息、是否虚拟运营商等。 二、手机号码归属地接口适用哪些场景? 例如:市场营销领域 (1)精准营销:企业可以通过手机号归属地查询接口了解客户的大致…...

DDei在线设计器-加载数据
加载数据 本示例演示了怎样加载已有的JSON到设计器中。 如需了解详细的API教程以及参数说明,请参考DDei文档 外部数据JSON demo.vue <script setup lang"ts"> import DDeiEditorView from "ddei-editor"; import { DDeiCoreStandLayou…...

NetLLM: Adapting Large Language Models for Networking.
目录 NetLLM: Adapting Large Language Models for Networking.GlossaryNotesINTRODUCTIONThe Main Roadmap so farNew Opportunities and ChallengesDesign and Contributions BACKGROUNDLearning-Based Networking AlgorithmsLarge Language Models MOTIVATIONNETLLM DESIGNM…...

基于Yolov8面部七种表情检测与识别C++模型部署
表情识别 七种表情识别是一个多学科交叉的研究领域,它结合了心理学、认知科学、计算机视觉和机器学习等学科的知识和技术。 基本概念 表情的定义:表情是人们在情绪体验时面部肌肉活动的结果,是人类情感交流的基本方式之一。基本表情理论&a…...

未确认融资费用含义及会计处理流程
文章目录 一、含义二、会计处理流程2.1、初始计量2.2、后续计量2.3、报表列式 三、实务中的注意事项 一、含义 未确认融资费用: 由于企业现有资金不足,购买资产时选择分期支付款项,导致实际支付的款项大于资产的购入价值,两者的差额就是由于…...

Linux配置go程序为service后台开机自启动
1.编写需要启动的项目路径以及简单配置 sudo nano /etc/systemd/system/go.service#定义服务的元数据和依赖关系。 [Unit] #这是对服务的简短描述。 DescriptionMy Go Service #network.target 是一个虚拟目标,它表示网络服务已经初始化完成。该指令告诉 systemd 在…...

汇舟问卷:完成16份调查,挣了40美金,换算后美滋滋
这个世界有太多的人30岁,35岁以后,当初没有去做自己想做的工作,没有花时间去坚持想做的工作,他们在选择这份想做的事业的前提被自己的父母朋友爱人阻断了。 他们告诉你,要努力的做好现在的工作,争取升职…...

Nacos 202407月RCE漏洞(0day)与复现
免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。 一、背景与…...
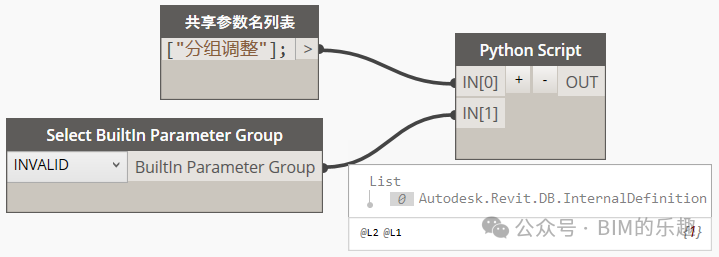
Dynamo修改共享参数绑定的分组——群问题整理005
Hello大家好!我是九哥~ 今天继续给大家分享一些短平快的小教程,是来自群里面的问题。 问题005:Dynamo修改共享参数绑定的分组 今天看到群里询问如何修改参数所在的分组,查了下API,项目参数是不行的,不过共享参数是允许ReInsert()的,那么就好办了。 然后在Document下…...

聚焦汽车软件开发与测试:静态代码扫描、单元测试与集成测试等方面的实践应用
2024年7月18-19日,龙智携汽车软件开发及管理解决方案创新亮相2024 ATC汽车软件与安全技术周。龙智技术支持部负责人&Atlassian认证专家叶燕秀、龙智功能安全高级工程师景玉鑫在活动主会场联合发表了精彩演讲,分享推动汽车软件开发与功能安全的创新实…...

「队列」实现FIFO队列(先进先出队列|queue)的功能 / 手撕数据结构(C++)
概述 队列,是一种基本的数据结构,也是一种数据适配器。它在底层上以链表方法实现。 队列的显著特点是他的添加元素与删除元素操作:先加入的元素总是被先弹出。 一个队列应该应该是这样的: --------------QUEUE-------------——…...

C++ STL中 `set` 和 `multiset` 简单对比
在 C STL 中,set 和 multiset 都是用于存储唯一或重复元素的关联容器,但它们在处理元素的唯一性和特性方面有显著的区别。以下是这两个容器的详细比较: 1. 数据结构 set:基于红黑树(自平衡的二叉搜索树)实…...

代码随想录算法训练营Day20 | Leetcode 235 二叉搜索树的最近公共祖先 Leetcode 701 二叉搜索树中的插入操作
Leetcode 235 二叉搜索树的最近公共祖先 题目链接:235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode) 代码随想录题解:代码随想录 (programmercarl.com) 思路:相比普通二叉树更简单,因为二叉搜索树的节点…...

第九届世界3D渲染大赛:赛程安排、赛事规则
第九届世界3D渲染大赛即将拉开帷幕,汇聚全球顶尖CG艺术家,展现最具有视觉盛宴的CG创作。那么该赛事的行程如何安排呢,赛事规则又是什么呢?本篇整理了赛事安排、赛事规则等内容,希望帮助大家。 赛事主题:Kin…...

RocketMQ5.0 Consumer Group
消费者分组的概念 消费者分组(Consumer Group)是指一组消费同一类消息的消费者实例。每个消费者分组有一个唯一的名称,用于标识该分组。消费者分组的设计使得消息能够被多个消费者实例并行消费,同时确保每条消息只被一个消费者实例…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
