Leetcode 第 135 场双周赛题解
Leetcode 第 135 场双周赛题解
- Leetcode 第 135 场双周赛题解
- 题目1:3222. 求出硬币游戏的赢家
- 思路
- 代码
- 复杂度分析
- 题目2:3223. 操作后字符串的最短长度
- 思路
- 代码
- 复杂度分析
- 题目3:3224. 使差值相等的最少数组改动次数
- 思路
- 代码
- 复杂度分析
- 题目4:3225. 网格图操作后的最大分数
- 思路
- 代码
- 复杂度分析
Leetcode 第 135 场双周赛题解
题目1:3222. 求出硬币游戏的赢家
思路
要用价值为 75 和 10 的硬币凑出价值总和为 115 的硬币,唯一的可能是 1 个 75 + 4 个 10。
如果一开始 Alice 就没法选,或者偶数轮后 Alice 没法选,那么 Bob 胜出,否则 Alice 胜出。
设 k=min(x, ⌊y/4⌋),这是能玩的回合数,判断 k 的奇偶性即可。
代码
/** @lc app=leetcode.cn id=3222 lang=cpp** [3222] 求出硬币游戏的赢家*/// @lc code=start
class Solution
{
public:string losingPlayer(int x, int y){return min(x, y / 4) % 2 ? "Alice" : "Bob";}
};
// @lc code=end
复杂度分析
时间复杂度:O(1)。
空间复杂度:O(1)。
题目2:3223. 操作后字符串的最短长度
思路
操作次数取决于每种字母的出现次数,与字母的位置无关。
假设某个字母出现了 c 次,那么操作后该字母最少能剩下多少?
根据题意,只有当 c≥3 时才能操作,每次操作可以把 c 减少 2。
- 如果 c=3, 5, 7,⋯ 是奇数,那么不断减 2,最终 c=1。
- 如果 c=4, 6, 8,⋯ 是偶数,那么不断减 2,最终 c=2。
累加每种字母最终剩下的 c,即为答案。
代码
/** @lc app=leetcode.cn id=3223 lang=cpp** [3223] 操作后字符串的最短长度*/// @lc code=start
class Solution
{
public:int minimumLength(string s){unordered_map<char, int> freq;for (char &c : s)freq[c]++;int ans = 0;for (auto &[c, cnt] : freq)ans += cnt % 2 ? 1 : 2;return ans;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n+∣Σ∣),其中 n 是字符串 s 的长度,∣Σ∣ 是字符集合的大小,本题字符均为小写字母,所以 ∣Σ∣=26。
空间复杂度:O(∣Σ∣),其中 ∣Σ∣ 是字符集合的大小,本题字符均为小写字母,所以 ∣Σ∣=26。
题目3:3224. 使差值相等的最少数组改动次数
思路
想一想,什么情况下答案是 0?什么情况下答案是 1?
如果答案是 0,意味着所有 ∣nums[i]−nums[n−1−i]∣ 都等于同一个数 X。
如果答案是 1,意味着有 n/2−1 个 ∣nums[i]−nums[n−1−i]∣ 都等于同一个数 X。我们只需要修改那对不相等的,设这两个数分别为 p=nums[i], q=nums[n−1−i]。
不妨设 p≤q,分类讨论:
- 如果修改 p,那么把 p 改成 0 可以让差值尽量大,此时差值为 q。
- 如果修改 q,那么把 q 改成 k 可以让差值尽量大,此时差值为 k−p。
- 如果 max(q,k−p)≥X,改其中一个数就行。
- 如果 max(q,k−p)<X,p 和 q 两个数都要改。
注意题目保证 n 是偶数。

代码
/** @lc app=leetcode.cn id=3224 lang=cpp** [3224] 使差值相等的最少数组改动次数*/// @lc code=start
class Solution
{
public:int minChanges(vector<int> &nums, int k){vector<int> cnt(k + 1), cnt2(k + 1);int n = nums.size();for (int i = 0; i < n / 2; i++){int p = nums[i], q = nums[n - 1 - i];if (p > q){ // 保证 p <= qswap(p, q);}cnt[q - p]++;cnt2[max(q, k - p)]++;}int ans = n;int sum2 = 0; // 统计有多少对 (p,q) 都要改for (int x = 0; x <= k; x++){// 其他 n/2-cnt[x] 对 (p,q) 至少要改一个数,在此基础上,有额外的 sum2 对 (p,q) 还要再改一个数ans = min(ans, n / 2 - cnt[x] + sum2);// 对于后面的更大的 x,当前的这 cnt2[x] 对 (p,q) 都要改sum2 += cnt2[x];}return ans;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n+k),其中 n 是数组 nums 的长度。
空间复杂度:O(k)。
题目4:3225. 网格图操作后的最大分数
思路
题解:【图解】DP 及其优化:从 n^4 到 n^3 到 n^2(Python/Java/C++/Go)
代码
#
# @lc app=leetcode.cn id=3225 lang=python3
#
# [3225] 网格图操作后的最大分数
## @lc code=start
class Solution:def maximumScore(self, grid: List[List[int]]) -> int:n = len(grid)# 每列的前缀和(从上到下)col_sum = [list(accumulate(col, initial=0)) for col in zip(*grid)]# pre 表示第 j+1 列的黑格个数# dec=True 意味着第 j+1 列的黑格个数 (pre) < 第 j+2 列的黑格个数@cachedef dfs(j: int, pre: int, dec: bool) -> int:if j < 0:return 0res = 0# 枚举第 j 列有 cur 个黑格for cur in range(n + 1):if cur == pre: # 情况一:相等# 没有可以计入总分的格子res = max(res, dfs(j - 1, cur, False))elif cur < pre: # 情况二:右边黑格多# 第 j 列的第 [cur, pre) 行的格子可以计入总分res = max(res, dfs(j - 1, cur, True) + col_sum[j][pre] - col_sum[j][cur])elif not dec: # 情况三:cur > pre >= 第 j+2 列的黑格个数# 第 j+1 列的第 [pre, cur) 行的格子可以计入总分res = max(res, dfs(j - 1, cur, False) + col_sum[j + 1][cur] - col_sum[j + 1][pre])elif pre == 0: # 情况四(凹形):cur > pre < 第 j+2 列的黑格个数# 此时第 j+2 列全黑最优(递归过程中一定可以枚举到这种情况)# 第 j+1 列全白是最优的,所以只需考虑 pre=0 的情况# 由于第 j+1 列在 dfs(j+1) 的情况二中已经统计过,这里不重复统计res = max(res, dfs(j - 1, cur, False))return res# 枚举第 n-1 列有 i 个黑格return max(dfs(n - 2, i, False) for i in range(n + 1))
# @lc code=end
复杂度分析
时间复杂度:O(n3),其中 n 是数组 grid 的长度。由于每个状态只会计算一次,动态规划的时间复杂度 = 状态个数 × 单个状态的计算时间。本题状态个数等于 O(n2),单个状态的计算时间为 O(n),所以动态规划的时间复杂度为 O(n3)。
空间复杂度:O(n2),其中 n 是数组 grid 的长度。
相关文章:

Leetcode 第 135 场双周赛题解
Leetcode 第 135 场双周赛题解 Leetcode 第 135 场双周赛题解题目1:3222. 求出硬币游戏的赢家思路代码复杂度分析 题目2:3223. 操作后字符串的最短长度思路代码复杂度分析 题目3:3224. 使差值相等的最少数组改动次数思路代码复杂度分析 题目4…...

rpc的原理
RPC(Remote Procedure Call,远程过程调用)是一种编程模型,它允许开发者像调用本地函数一样调用位于不同进程或者不同机器上的函数或服务。这种抽象简化了分布式系统的开发,使得开发人员无需关注底层网络通信细节&#…...

【无线通信发展史-第二篇】,带你走进查利·奥古斯丁·库仑的世界,了解(库伦定律)-(扭秤实验)-(如何测量出静电力常量)
前言:用这几个问答形式来解读下我这个系列的来龙去脉。如果大家觉得本篇文章不水的话希望帮忙点赞收藏加关注,你们的鼓舞是我继续更新的动力。 我为什么会写这个系列呢? 首先肯定是因为我本身就是一名从业通信者,想着更加了解自…...

CAPL使用结构体的方式组装一条DoIP车辆声明消息(方法2)
在文章CAPL使用结构体的方式组装一条DoIP车辆声明消息(方法1)中,我们声明一个结构体DoIPMessage表示完整的DoIP车辆声明消息: 上半部分是DoIP报头通用部分(也就是所有类型的DoIP消息都有的),而payload是每个类型的DoIP消息独有的部分,对于车辆声明消息来说,用另一个结…...

基于Matlab的车牌识别系统设计与实现
基于Matlab的车牌识别系统设计与实现 摘要 随着智能交通系统的不断演进,车牌识别技术已成为提升交通管理效率与准确性的关键。本文深入探讨了基于Matlab平台的车牌识别系统设计与实现,该系统通过精细的图像预处理、高效的车牌定位算法、精准的字符分割…...

使用Cisco进行模拟RIP路由协议配置
实验四 RIP路由协议配置 文章目录 实验四 RIP路由协议配置1.实验目的2.实验流程3.RIPv1实验步骤4.RIPv2实验步骤 1.实验目的 1)理解RIP路由的原理 2)掌握RIP路由的配置方法 2.实验流程 开始→布置拓扑→配置IP地址→配置并验证RIPv1→配置并验证RIPv2…...

段页式存储-系统架构师(三十七)
1、一个完整的系统需要从不同的角度进行描述,下图属于软件架构设计中的(),用于()视图来描述软件系统。 问题1 A对象图 B时序图 C构件图 D类图 问题2 A进程 B开发 C物理 D逻辑 解析: 从…...

通过指令深入了解Linux
文章目录 1.简单介绍XShell1.1下载安装XShell1.2 使用XShell登录主机1.3 XShell下的复制粘贴 2. Linux下的基本指令2.1 ls指令2.1.1 对文件的理解2.1.2 目录下的隐藏文件 2.2 pwd指令2.3 cd指令2.3.1 Linux下目录结构的认识 2.4 touch指令2.5 mkdir指令2.6 clear指令 1.简单介绍…...
IP探针双端源码
源码耗费两年半的制作过程 将源码上传至你的服务器或你的主机 可以对接其他东西或者网站其他语言 使用方法 1.参数使用 http://域名/sc.php?id这是生成端 http://域名/sc1.php?id这是生成端生成的链接可以跳转链接 http://域名/ck.php?id这是查看IP 生成端,生成完…...

高中数学学科知识与教学能力
梳理...

Flink 实时数仓(七)【DWS 层搭建(一)流量域汇总表创建】
前言 今天开始 DWS 层的搭建,不知不觉又是周一,都忘了昨天是周末,近两年对我来说,周六日晚上八九点能打一小会篮球就算一周的休息了。不得不说自己真的是天生打工体质,每天不管多累,晚上十二点睡࿰…...

Python和PyCharm的安装激活及Python新手入门指南
一、软件介绍 Python 是一种解释型、面向对象、动态数据类型的高级程序设计语言。于 1989 年底由 Guido van Rossum 发明,第一个公开发行版发行于 1991 年。 当然也有很多小伙伴不清楚python与pycharm的区别和联系,接下来给大家简单介绍一下࿱…...

Apache Flink窗口机制解析:滚动窗口与滑动窗口的比较与应用
Apache Flink是一个开源的流处理框架,用于实现大规模数据流的处理和分析。在处理数据流时,窗口操作是一种常见的方法,它允许对数据流中连续的项目进行分组。Flink提供了多种窗口类型,其中滚动窗口(Tumbling Window&…...

为什么《程序员修炼之道》评分能到 9.1?
大家好,我是 方圆。开始接触到《程序员修炼之道:通向务实的最高境界》这本书是在豆瓣图书的高分榜单上,它的评分高达 9.1,其中有条蛮有意思的书评非常吸引我:“这本书我读过 5 遍信不信,每个字都磨出了感情…...

接口自动化测试框架中动态参数接口,加密接口,签名接口你们是怎么处理的?
动态参数:可通过热加载形式(在代码执行过中自动去yaml里面执行外部的函数) 接口测试加密解密简介: 对称加密(私钥加密,只有一个密钥)AES,DES,BASE64 特点是:加密和解密有相同的密钥…...

【hadoop】常用命令
集群信息 查看hadoop版本 hadoop version查询hdfs系统中的namenode # 方式一 hdfs getconf -namenodes# 方式二 hdfs getconf -confKey dfs.namenode.http-address获取NameNode restful接口 hdfs getconf -confKey dfs.namenode.http-address hdfs getconf -confKey dfs.na…...

时间同步--- ntp与ptp
时间同步 1. 什么是NTP时间?什么是PTP时间? NTP时间(Network Time Protocol 时间): NTP即网络时间协议(Network Time Protocol),它是一种用于同步计算机时间的网络协议。NTP可以将所有参与的计…...

CSDN 僵尸粉 机器人
CSDN 僵尸粉 机器人 1. 前言 不知道什么时候开始每天创作2篇就有1500流量爆光,每次都能收获一些关注和收藏,感觉还是挻开心的感觉CSDN人气还是挻可以的以前各把月一个收藏和关注都没有写的动力了。 2. 正文 后面又连接做了2天的每日创建2篇任务&…...

【Material-UI】File Upload Button 组件详解
文章目录 一、基础实现1. component"label"2. 隐藏的输入元素 二、样式和交互增强1. 自定义按钮样式2. 交互提示 三、支持多文件上传四、无障碍性(Accessibility)1. 提供 aria-label 或 aria-labelledby2. 支持键盘导航 五、高级用法和集成1. …...
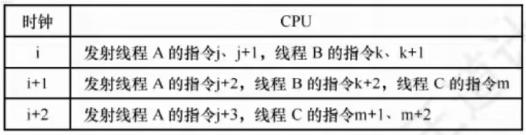
计算机组成原理 - 中央处理器
中央处理器 考纲内容 CPU的功能和基本结构指令执行过程数据通路的功能和基本结构控制器的功能和工作原理异常和中断机制 异常和终端的基本概念;异常和中断的分类;异常和中断的检测与响应指令流水线 指令流水线的基本概念;指令流水线的基本实…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
