【无线通信发展史-第二篇】，带你走进查利·奥古斯丁·库仑的世界，了解（库伦定律）-（扭秤实验）-（如何测量出静电力常量）

     前言：用这几个问答形式来解读下我这个系列的来龙去脉。如果大家觉得本篇文章不水的话希望帮忙点赞收藏加关注，你们的鼓舞是我继续更新的动力。

1. 我为什么会写这个系列呢？

首先肯定是因为我本身就是一名从业通信者，想着更加了解自己专业的知识，所以更想着从头开始了解通信的来源以及在每一个时代的发展进程。

1. 为什么会从头开始写通信？

我最早是学习了中华上下五千年，应该说朝代史，这个算个人兴趣，从夏朝开始到清朝，古代史的结束，后面我还看了近代史的历程，所以在要学习通信历史的时候我也采用了或者方法，想一步一步的去源头开始，看看通信是怎么发展到今天，这是个很好的主意。也是一个很好的学习方法。

1. 你觉得这个系列有什么优势？

我觉得优势就是我以身代入，一步一个脚印的去学习，中间碰到的问题也会扩展到再去学习解决，很好的解决了作为初学者一些问题的困恼，不至于一笔跳过很多东西，所以很适合后面的读者跟随我的学习步伐一起向前。

---

 前沿：

        查利·奥古斯丁·库仑（1736年6月14日—1806年8月23日），主要贡献有扭秤实验、库仑定律、库伦土压力理论等。
        电荷的单位库仑就是以他的姓氏命名的。简称库，符号C。定义：若导线中载有1安培的稳定电流，则在1秒内通过导线横截面的电量为1库仑。

        库仑定律是电学发展史上的第一个定量规律，是电磁学和电磁场理论的基本定律之一。它使电学的研究从定性进入定量阶段。
留下不少著作，其中最主要的有《电气与磁性》一书。

库仑，他让电学成为一门现代科学_澎湃号·湃客_澎湃新闻-The Paper

（1）库伦定律

        库仑定律是静止点电荷相互作用力的规律。

        真空中两个静止的点电荷之间的相互作用力与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上，同名电荷相斥，异名电荷相吸。

        点电荷：点电荷是带电体的一种理想模型。如果在研究的问题中，带电体的形状 、大小以及电荷分布可以忽略不计 ，即可将它看作是一个几何点，则这样的带电体就是点电荷。(“点电荷”就是带电体，是一个没有大小和形状的几何点)

        什么是点电荷？任何带电体都有形状和大小，其上的电荷也不会集中在一点上。当带电体间的距离比它们自身的大小大得多，以至带电体的形状、大小及电荷分布状况对它们之间的作用力的影响可以忽略时，这样的带电体就可以看做带电的点，叫做点电荷（point charge）。可见，点电荷类似于力学中的质点，也是一种理想化的物理模型。

        当各个物理量都采用国际制单位时，静电力常量是的单位是由公式中 F、q、r 的单位确定的，而它们在国际单位制中的单位是牛（N）、库（C）、米（m）。

---

（2）如何测量库伦力的大小？-扭秤实验（很微弱，难于感受到）

第一章 2 库仑定律 (enjoyphysics.cn)

第九章 第二节 电荷的相互作用 库仑定律 (enjoyphysics.cn)

3.3 库仑定律的发现 (enjoyphysics.cn)

        库仑定律是电磁学的基本定律之一，发现于 1785 年。它是继牛顿引力定律之后的第二个作用力与距离平方成反比的物理规律，两个规律有相似性。

        人们最早是通过电荷之间的相互作用来认识电荷的。在牛顿力学成功地研究了物体的机械运动之后，18世纪的物理学家们很自然地把带电物体在相互作用中的表现，与力学中的作用力联系起来了。

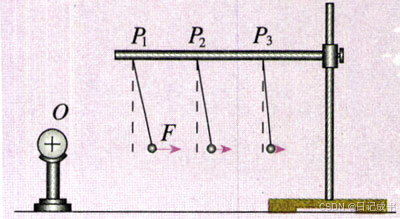
        O是一个带正电的物体。把系在丝线上的带正电的小球先后挂在图1.2-1中P1、P2、P3等位置，比较小球在不同位置所受带电体的作用力的大小。这个力的大小可以通过丝线偏离竖直方向的角度显示出来。

        使小球处于同一位置，增大或减少小球所带的电荷量，比较小球所受作用力的大小。哪些因素影响电荷间的相互作用力？这些因素对作用力的大小有什么影响？

        实验表明，电荷之间的作用力随着电荷量的增大而增太，随着距离的增大而减小。这隐约使我们猜想：电荷之间的作用力会不会与万有引力具有相似的形式呢？也就是说，带电物体之间的相互作用力，会不会与它们电荷量的乘积成正比，与它们之间距离的二次方成反比？

先定性探究静电力的大小由哪些因素决定，知道电荷间相互作用力与带电体间的距离和两电荷的电荷量大小有关。

        事实上，电荷之间的作用力与引力的相似性早已引起当年一些研究者的注意，卡文迪许和普里斯特利等人都确信“平方反比”规律适用于电荷间的力。

“平方反比”规律：下一篇文章再详细开展。

         如何定量探究电荷间相互作用力的规律？

        18 世纪中叶以前，研究带电体之间的静电力遇到三大困难：

        一是任意带电体上的电荷分布难以确定，无法确定相互作用的电荷间的距离；（根据电荷在金属球表面上均匀分布的特点，把金属球上的电荷想象成集中在球心的“ 点电荷”。这一模型就解决了测量带电体之间距离的问题。）

        二是这种静电力非常小，没有测量如此小力的工具；（库仑设计制作了一台能够测出微弱作用力的扭秤，用以测量两个同种点电荷之间的作用力，库仑从牛顿的万有引力规律得到启发，用类比的方法来研究电荷间的相互作用。）

        三是当时还没有度量电荷量的单位，也就无法确定电荷量的大小。

 

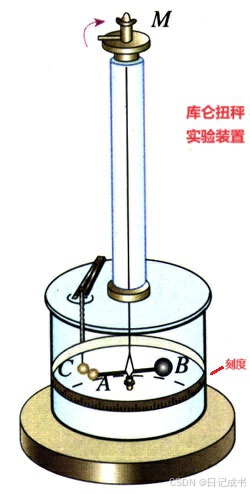
         如图所示，细银丝的下端悬挂一根绝缘棒，棒的一端是一个带电的金属小球A，另一端有一个不带电的球B，B与A所受的重力平衡。当把另一个带电的金属球C插入容器并使它靠近A时，A和C之间的作用力使悬丝扭转，通过悬丝扭转的角度可以比较力的大小。改变A和C之间的距离r，记录每次悬丝扭转的角度，便可找到力F与距离r的关系，结果是力F与距离r的二次方成反比。即

         根据库仑对电荷间的相互作用力的研究历史，当年库仑得到表 9–2 所示的三组实验数据。他分析在电荷量一定的条件下弹性扭丝的扭转角 θ 与两带电体 A、C 之间距离 r 的关系，得到弹性扭丝的扭转角 θ 与 r 的二次方成反比 (θ∝1/r2)。再根据电荷间的相互作用力 F 与扭丝的扭转角 θ 成正比（F ∝ θ），并以 9 个刻度对应 1 单位的距离，由表 9–2 的数据可得两带电球间的距离与静电力之间的关系，如表 9–3 所示。

        库仑用扭秤进行实验，通过和万有引力的类比较快得出了电荷间作用力F跟距离r的二次方成反比

的规律。如仅靠实验数据的积累，也许这个规律的发现可能会被推迟。

        在库仑那个年代，还不知道怎样测量物体所带的电荷量，甚至连电荷量的单位都没有。库仑发现，两个相同的带电金属小球互相接触后，它们对相隔同样距离的第三个带电小球的作用力相等，所以他断定这两个小球所带的电荷量相等。如果把一个带电金属小球与另一个不带电的完全相同的金属小球接触，前者的电荷量就会分给后者一半。库仑就用这个方法，把带电小球的电荷量q分为： 

         根据扭丝的扭转角θ和两带电体之间距离r的关系，得出“带同号电荷的两球之间的排斥力与两球中心之间的距离的二次方成反比”的结论。
        后来库仑又通过电引力扭摆实验进一步证明了异号电荷间存在的吸引力也满足二次方反比的关系，总结出了库仑定律，并测出了静电力常量。

①库仑的电摆实验装置，从库仑的发现经过可以看出，平方反比的关系自始至终对他的实验起着指导作用。

---

（3）如何测量出静电力常量？(涉及到多个公式，本次就不深入了解，后续会有交集再详细展开)

参考：2015年3月《物理通报》段书林论文《静电力常量的来龙去脉》

        静电力常量是一个无误差常数，它的数值约为k=8.987551×109N·m2/C2。既不是库仑通过扭秤测出来的，也不是后人通过库仑扭秤测出来的，而是通过麦克斯韦的相关理论算出来的。 

---

预告：下一篇——翻到前面牛顿·万有引力定律，去详细了解下源头，了解“平方反比”规律

1 #include "stdio.h"
2 void main()
3 {
4     int time;
5     for (time=1;time<=10;time++)
6     printf("%d、喜欢的帮忙点赞收藏加关注哦！\n",time);
7 }