机器学习:识别AI,GraphRAG,LoRA,线性变换,特征
1.AI识别
- 1.bitgrit 生成式 AI API 文档
生成式 AI 假图像检测 API 可用于以编程方式检测假图像(即由生成式 AI 创建的图像)。 - 2.X Virality Prediction API 旨在预测推文的潜在病毒式传播力。
- https://bitgrit.net/api/docs/x_virality_prediction
2.GraphRAG
所有性能改进技术都有一个缺陷:token 的使用和推理时间都会增加。
支持 GraphRAG 的基本流程是建立在先前对图机器学习的研究和代码库上的:LLM 处理全部私有数据集,为源数据中所有实体和关系创建引用,并将其用于创建 LLM 生成的知识图谱。利用生成的图谱创建自下而上的聚类,将数据分层并组织成语义聚类(在图三中由颜色标识)。这种划分让预先总结语义概念和主题成为可能,从而更全面地理解数据集。在查询时,两种结构均被用于填充 LLM 回答问题时的上下文窗口。
3.什么是低秩自适应(LoRA)?
LoRA 是一种加速 LLM 微调同时消耗更少内存的技术。

这不涉及对整个基础模型进行微调,因为这可能需要耗费大量的时间和金钱。
相反,它会向模型中添加少量可训练参数,同时保持原始模型参数不变。
为什么选择 LoRA?
尽管我们使用 LoRA 为模型添加了更多层,但它实际上有助于节省内存。
这是因为与大模型相比,较小的层(A 和 B)需要学习的参数较少,而可训练参数较少意味着需要存储的优化器变量较少。
因此,尽管整体模型看起来更大,但就内存使用而言实际上更高效。
什么是等级?
秩决定了添加到 LLM 原始权重的可训练矩阵的维度。它控制微调的表达能力和精度。
等级越高 = 可能的变化越详细,可训练的参数越多
等级越低 = 计算开销越少,但适应的精度可能会更低
任何人工智能问题中最重要的因素是数据
4. 线性变换

线性变换是两个向量空间之间的映射V → W,保留向量加法和标量乘法的运算。
实际上,将矩阵A应用于向量x以获得另一个向量y(通过操作Ax = y)是一种线性变换。
import numpy as np
import matplotlib.pyplot as plt# Linear Transformation of a Square
T = np.array([[1, 2], [2, 1]]) # Transformation matrix
square = np.array([[0, 0, 1, 1, 0], [0, 1, 1, 0, 0]]) # Original square
transformed_square = np.dot(T, square) # Apply transformation# Plot Original and Transformed Square
plt.figure(figsize=(8, 4))# Original Square
plt.subplot(1, 2, 1)
plt.plot(square[0], square[1], 'o-', color='blue')
plt.title('Original Square')
plt.xlim(-1, 3)
plt.ylim(-1, 3)
plt.axhline(0, color='grey', linewidth=0.5)
plt.axvline(0, color='grey', linewidth=0.5)
plt.grid(True)# Transformed Square
plt.subplot(1, 2, 2)
plt.plot(transformed_square[0], transformed_square[1], 'o-', color='red')
plt.title('Transformed Square')
plt.xlim(-1, 3)
plt.ylim(-1, 3)
plt.axhline(0, color='grey', linewidth=0.5)
plt.axvline(0, color='grey', linewidth=0.5)
plt.grid(True)plt.show()

线性变换经常用于:
降维:PCA利用线性变换将高维数据映射到低维空间
数据变换:对数据集进行规范化或标准化是一种线性变换
特征工程:通过组合现有特征来创建新特征。
5. 特征向量和特征值
特征向量和特征值表示变换的“轴”。
特征向量是经过线性变换后方向不变的输入。即使方向不变,大小也可能变。这个大小,即特征向量放大或缩小的量,就是特征值。
想象一下当你旋转地球仪时,除了两极之外,每个位置都朝向一个新的方向。它们的方向不会改变。
这是特征向量的直观示例。
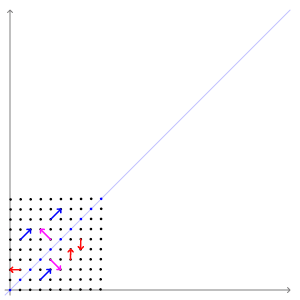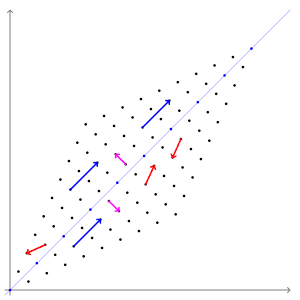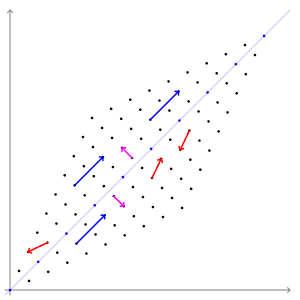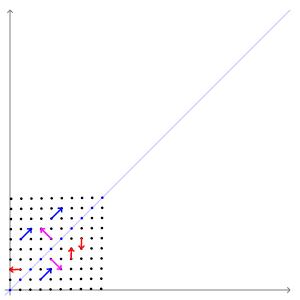
形式上,对于矩阵A和向量v,如果Av = λv,则λ是特征值,v是A的特征向量。
import numpy as np
import matplotlib.pyplot as plt# Eigenvectors and Eigenvalues
A = np.array([[1, 2], [2, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)print_matrix(A)# Plotting
fig, ax = plt.subplots()# Origin
origin = [0, 0]# Plot each eigenvector
for i in range(len(eigenvalues)):ax.quiver(*origin, eigenvectors[0, i], eigenvectors[1, i], scale=3, scale_units='xy', angles='xy')ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_aspect('equal')
ax.grid(True)
ax.set_title('Eigenvectors of A')plt.show()

相关文章:

机器学习:识别AI,GraphRAG,LoRA,线性变换,特征
1.AI识别 1.bitgrit 生成式 AI API 文档 生成式 AI 假图像检测 API 可用于以编程方式检测假图像(即由生成式 AI 创建的图像)。2.X Virality Prediction API 旨在预测推文的潜在病毒式传播力。https://bitgrit.net/api/docs/x_virality_prediction 2.Gr…...

阿里云SMS服务C++ SDK编译及调试关键点记录
一. 阿里云SMS服务开通及准备工作 在阿里云官网上完成这部分的工作 1. 申请资质 个人or企业 我这里是用的企业资质 2. 申请签名 企业资质认证成功后,会自动赠送一个用于测试的短信签名 也可以自己再进行申请,需要等待审核。 3. 申请短信模板 企…...
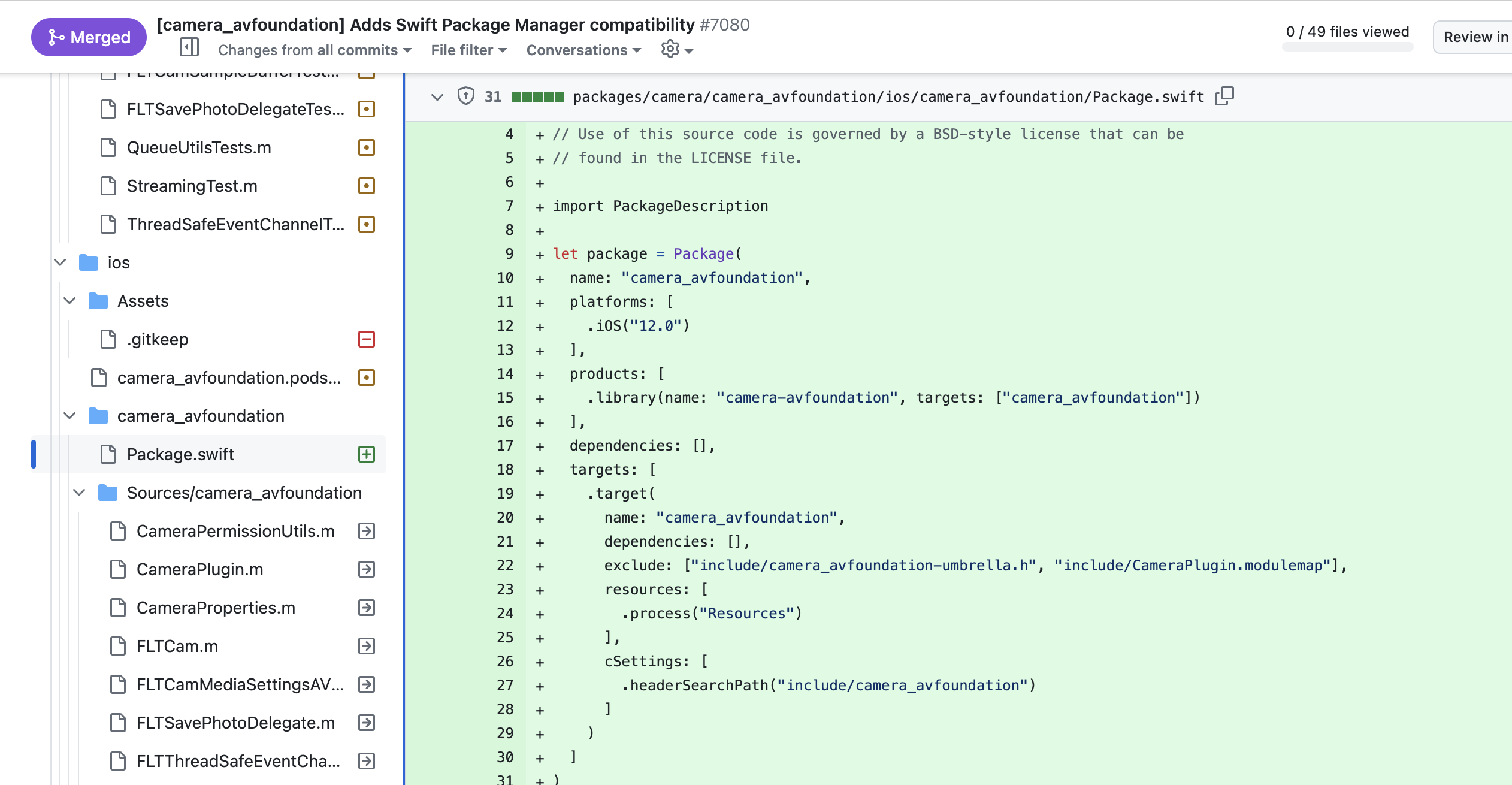
Flutter 正在迁移到 Swift Package Manager ,未来会弃用 CocoaPods 吗?
什么是 Swift Package Manager ?其实 Swift Package Manager (SwiftPM) 出现已经挺长一段时间了,我记得第一次听说 SwiftPM 的时候,应该还是在 2016 年,那时候 Swift 3 刚发布,不过正式出场应该还是在 2018 年的 Apple…...

PDF——分割pdf的10个工具
PDF分割器是一种可用于将PDF文档分割成更小的文档甚至单个页面的工具。分割 PDF 文档的主要原因是为了更容易共享。 但该过程的成功取决于您用于拆分 PDF 的工具。较简单的工具仅提供几个选项,可能并不适合所有类型的文档。我们将在本文中列出的 10 个最佳 PDF 分割…...

深入解析 Nginx 反向代理:配置、优化与故障排除
深入解析 Nginx 反向代理:配置、优化与故障排除 Nginx 是一个高性能的 HTTP 和反向代理服务器,它以其高并发和高可扩展性在业界享有盛誉。反向代理是 Nginx 的重要功能之一,通过反向代理可以实现负载均衡、安全代理、缓存等多种用途。本篇文…...

深度学习入门(一):感知机与输入数据
单层感知机与多层感知机 单层感知机(Single-Layer Perceptron)和多层感知机(Multi-Layer Perceptron,简称MLP)是神经网络的基本形式,用于执行各种机器学习任务,包括分类和回归。它们都基于早期…...

kubernetes 集群组件介绍
kubernetes 集群组件介绍 Kubernetes 架构 在Kubernetes(k8s)集群中,主节点(Master Node)和工作节点(Worker Node)都运行特定的软件组件,它们共同管理和运行容器化的应用程序。以下…...

Java | Leetcode Java题解之第327题区间和的个数
题目: 题解: class Solution {public int countRangeSum(int[] nums, int lower, int upper) {long sum 0;long[] preSum new long[nums.length 1];for (int i 0; i < nums.length; i) {sum nums[i];preSum[i 1] sum;}BalancedTree treap ne…...

开发一个MutatingWebhook
介绍 Webhook就是一种HTTP回调,用于在某种情况下执行某些动作,Webhook不是K8S独有的,很多场景下都可以进行Webhook,比如在提交完代码后调用一个Webhook自动构建docker镜像 准入 Webhook 是一种用于接收准入请求并对其进行处理的…...

【leetcode详解】另一棵树的子树 (C++递归:思路精析 过程反思)
思路详解: 总体框架: 对root树进行先序遍历,如果当前结点(记为cur)的值和subRoot的根节点值相等时,就开始判断 以cur为根节点的树 和 子树 是否结构一样? 如何判断两棵树是否结构完全相同? …...

物联网遇到人工智能,极快的加速物联网时代
近些年物联网已成为众多科技企业的战略目标,如智能家居等,在未来,手机、传感器等智能设备都走进了生活当中,据数据显示已经有80%以上的的智能手机配备了人工智能。人工智能也不陌生,自动驾驶、人脸识别这些应用场景都是…...

Vue3+Ts项目中经常遇到导入组件,vscode报无法找到模块xxx,xxx隐式拥有 “any“ 类型解决办法~
1、报错截图: 2、解决办法:在确保路径正确的情况下,你会在 src 目录下找到一个名为 env.d.ts 的文件(或者类似的名称)。在这个文件中,你可以声明 .vue 文件的模块类型。例如:(这告诉 TypeScript…...

郑州轻工业大学zzulioj1151~1159合集
郑州轻工业大学zzulioj1151~1159合集 郑州轻工业大学zzulioj1151~1159合集 1150数数多少个整数1151大整数加法题目描述1152: 二分搜索1153简易版最长序列题目描述1154: 校门外的树1155字符串比较 多实例题目描述1156单数变复数题目描述1157连续的n个1题目描述1158又是排序&…...
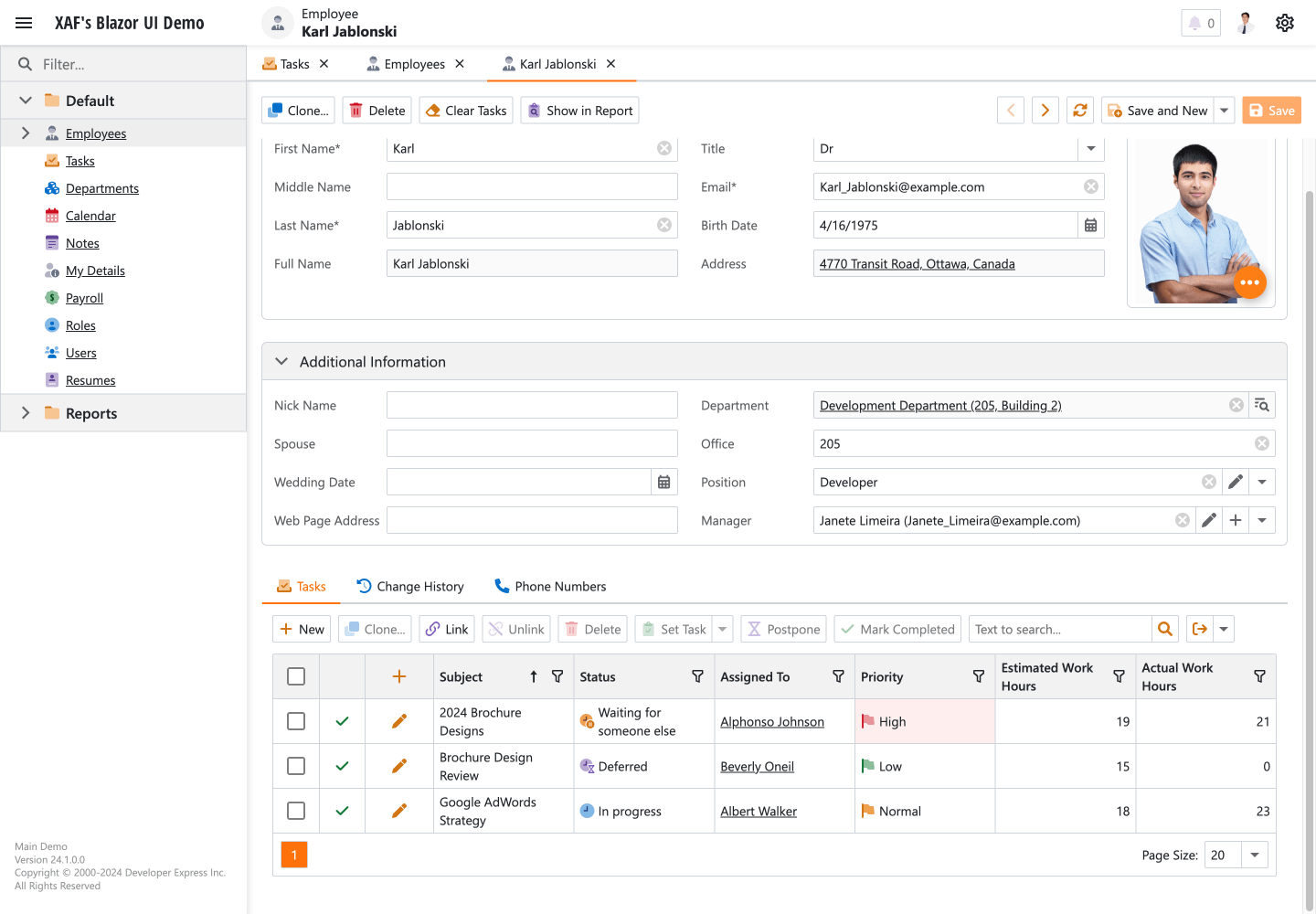
开发框架DevExpress XAF v24.2产品路线图预览——增强跨平台性
DevExpress XAF是一款强大的现代应用程序框架,允许同时开发ASP.NET和WinForms。XAF采用模块化设计,开发人员可以选择内建模块,也可以自行创建,从而以更快的速度和比开发人员当前更强有力的方式创建应用程序。 DevExpress XAF是一…...

程序员短视频上瘾综合症
一、是你疯了还是面试官疯了? 最近有两个学员咨询问题,把我给整得苦笑不得。大家来看看,你有没有同样的症状。 第一个学员说去一家公司面试,第一轮面试聊得挺好的。第二轮面试自我感觉良好,但是被面试官给Diss…...

image.convert()函数转换格式及显示图像的RGB三通道图像
引 言 视觉任务处理的图片按照图像通道深度分为单通道图像和多通道图像。单通道图像有grayscale灰度图、binary二值图、PNG图,多通道图像有三通道24位真彩色RGB图,8位伪彩色图像,YCbCr图像等。本文先介绍各种格式图像的特点,随后讲…...
)
C语言 ——— 在控制台实现扫雷游戏(一次展开一片,递归实现)
前言 两个数组,一个用来显示在控制台上,一个用来存放雷 两个数组的实际大小为11 * 11 ,而为了方便排查雷的个数,实际使用范围是9 * 9 test.c #include"mine_sweeping.h"void game() {// 存放雷char mine[ROWS][COL…...

el7升级Apache模块编译
1.背景 接续https://blog.csdn.net/nanhai_happy/article/details/140566070,由于升级升级Apache过程中,发现需要使用的mod_wsgi、mod_systemd和mod_cgi模块缺失,故接着解决继续编译生成。 2. 编译mod_cgi、mod_system 2.1 安装依赖 yum …...

Linux系统下的日志管理与ELK Stack实践
关于“Linux系统下的日志管理与ELK Stack实践”,这个主题涵盖了如何在Linux环境中高效地收集、解析、存储及分析日志,以及如何利用ELK Stack(Elasticsearch、Logstash、Kibana)这套工具来实现日志的集中管理和可视化。下面我会简要…...

C++入门基础知识
在之前我们学习了C语言和初阶数据结构的相关知识,现在已经有了一定的代码能力和对数据结构也有了基础的认识,接下来我们将进入到新的专题当中,这个专题就是C。在C中我们需要花费更大的精力和更长的时间去学习这门建立在C语言基础之上的计算机…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
