二叉树刷题,bfs刷题
有些题目,你按照拍脑袋的方式去做,可能发现需要在递归代码中调用其他递归函数计算字数的信息。一般来说,出现这种情况时你可以考虑用后序遍历的思维方式来优化算法,利用后序遍历传递子树的信息,避免过高的时间复杂度。
遍历,对每一个结点进行操作,可以是找这个结点的旁边结点也可以是累加之类的操作。
所以最好的解法是反过来思考,只计算一次最大深度,计算的过程中在后序遍历位置顺便判断二叉树是否平衡:
对于每个节点,先算出来左右子树的最大高度,然后在后序遍历的位置根据左右子树的最大高度判断平衡性。 后序位置的妙用
110. 平衡二叉树
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:self._is_balanced = True self.maxDepth(root)return self._is_balanced #求最大深度是分解问题的思路,只要不是命名为traverse都是分解问题的思路def maxDepth(self, root) -> int:if root is None:return 0 leftMaxDepth = self.maxDepth(root.left)rightMaxDepth = self.maxDepth(root.right)if abs(rightMaxDepth - leftMaxDepth) > 1:self._is_balanced = False #在后序位置判断二叉树是否平衡,return 1 + max(leftMaxDepth, rightMaxDepth)这道题属于二叉树的平衡性检查问题,可以看作是结合了“遍历”和“分解”两种思路的题目。
- 遍历:在遍历整棵二叉树的过程中,我们在后序遍历的位置对每个节点的左右子树的深度进行计算,并检查它们的深度差是否超过1。如果深度差超过1,则这棵树不是平衡的。
- 分解:对于每一个节点,我们通过递归计算其左子树和右子树的最大深度,然后用这些结果来判断当前节点的平衡性。每个节点的平衡性都是通过分解其左右子树来确定的。
因此,这道题可以看作是利用遍历的方式来实现分解的思路:
- 遍历:遍历树的每个节点,检查每个节点的左右子树深度差。
- 分解:每个节点的平衡性判断是基于其左右子树的深度(子问题)的解决结果。
#遍历,再加上子问题, 每棵树的最大子树,取决于最大左右子树的最大值。
1325. 删除给定值的叶子节点
删除指定值的叶子节点,其实就是遍历所有的叶子节点,然后判断是否需要删除;删除叶子节点也很简单,return null 让父节点接收即可。
难点在于他这个删除操作是循环的,一直删到叶子结点不存在 target 为止。这里要用到前文 手把手刷二叉树总结篇 说过的后序位置的妙用了:
一个节点要在后序位置接收左右子树的返回值,才能知道自己的叶子节点是否都被删掉了,以此判断自己是不是变成了叶子节点。
class Solution:#函数定义,输入一棵树,返回的是删除了目标值叶子的树 每次用分解问题的思路都把这个函数定义想明白def removeLeafNodes(self, root: Optional[TreeNode], target: int) -> Optional[TreeNode]:if root is None:return None root.left = self.removeLeafNodes(root.left, target)root.right = self.removeLeafNodes(root.right, target)if root.val == target and root.left is None and root.right is None:return Nonereturn root 仔细观察,前中后序位置的代码,能力依次增强。
前序位置的代码只能从函数参数中获取父节点传递来的数据。
中序位置的代码不仅可以获取参数数据,还可以获取到左子树通过函数返回值传递回来的数据。
后序位置的代码最强,不仅可以获取参数数据,还可以同时获取到左右子树通过函数返回值传递回来的数据。
所以,某些情况下把代码移到后序位置效率最高;有些事情,只有后序位置的代码能做。
那么换句话说,一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
二叉树大部分题目都可以用递归的算法解决,但少部分题目用递归比较麻烦的话,我们可以考虑使用层序遍历的方式解决。
熟练bfs,多敲几遍模板
你可以认为二叉堆是一种特殊的二叉树,这棵二叉树上的任意节点的值,都必须大于等于(或小于等于)其左右子树所有节点的值。如果是大于等于,我们称之为「大顶堆」,如果是小于等于,我们称之为「小顶堆」。
对于小顶堆,每个节点下方的所有节点的值都比它大,那么不难想象根节点就是整棵树上的最小值。同理,大顶堆的根节点就是整棵树上的最大值。所以二叉堆可以辅助我们快速找到最大值或最小值。
1104. 二叉树寻路
class Solution:def pathInZigZagTree(self, label: int) -> List[int]: #输入一个标号,获得路径path = []while label >= 1:path.append(label)label = label // 2 #最开始的计算方法是一只除以2,余数略去得到答案 if label == 0:break depth = self.log(label) #求这一层的深度range_ = self.getLevelRange(depth) #求这一层的范围label = range_[1] - (label - range_[0]) path.reverse()return path def getLevelRange(self, n) -> List:p = 2 **n return [p, 2 * p - 1] #获取这一层的范围def log(self, x) -> int: #这里获得的层数,原始是第0层if x == 0 :return 0 return int(math.log(x) / math.log(2)) #python中的log是以e为底,所以写一个log函数,求以2为底的值
在 LeetCode 刷题时,通常编写的是实例方法。LeetCode 提供的代码框架通常要求在一个类中定义一个实例方法,然后实例化这个类并调用该方法来解决问题。
典型的 LeetCode 代码框架
以下是 LeetCode 提供的一个常见框架的例子,通常在一个类中定义一个实例方法
类方法是 Python 类中的一种方法,它属于类本身,而不是某个特定的实例。类方法使用 @classmethod 装饰器定义,并且第一个参数是 cls,代表类本身。这允许类方法访问和修改类级别的属性,而不是实例级别的属性
静态方法
静态方法不需要 self 或 cls 参数。它们是独立于类和实例的函数,通常用于定义一些工具函数。
class MyClass:@staticmethoddef add(a, b):return a + bprint(MyClass.add(5, 3)) # 输出: 8
总结
- 实例方法 使用
self来访问和修改实例属性和方法。 - 类方法 使用
cls来访问类属性和方法。 - 静态方法 不需要
self或cls参数,因为它们不访问类或实例的任何属性或方法。
访问实例方法需要使用 self,这并不是类方法的特性,而是实例方法的特性。类方法和静态方法不使用 self,类方法使用 cls,静态方法不使用任何特殊的类或实例引用
实例方法: 实例方法可以访问实例属性和类属性。它们主要用于操作实例数据。
python复制代码class MyClass:def __init__(self, value):self.value = valuedef instance_method(self):print(f"Instance value: {self.value}")obj = MyClass(10)
obj.instance_method() # Instance value: 10
类方法: 类方法只能访问类属性,不能直接访问实例属性。它们主要用于操作类级别的数据或执行与类相关的操作。
python复制代码class MyClass:class_variable = "class value"@classmethoddef class_method(cls):print(f"Class variable: {cls.class_variable}")MyClass.class_method() # Class variable: class value
实例方法可以访问实例属性和类属性。它们主要用于操作实例数据。 类方法: 类方法只能访问类属性,不能直接访问实例属性。它们主要用于操作类级别的数据或执行与类相关的操作。
在Python中,可以在一个类内部定义另一个类,这种做法是合理的,尤其是当内嵌类(nested class)只与包含它的外部类相关时。这种设计有助于将相关的逻辑组织在一起,使代码更清晰和易于维护。
为什么需要使用 self 来引用 Pair 类
- 类的作用域:
Pair类是Solution类的一个嵌套类。为了在Solution类的方法中引用Pair类,你需要通过self来访问它,因为Pair是Solution类的一个成员。
- 实例属性的访问:
- 在 Python 中,
self关键字用于访问类的实例属性和方法。在这个例子中,self.Pair表示Pair类是Solution类的一个属性。
- 在 Python 中,
- 避免名称冲突:
- 使用
self可以避免名称冲突,确保引用的类或方法是当前类的成员,而不是全局作用域中的其他定义。
- 使用
- ·
515. 在每个树行中找最大值
class Solution:def largestValues(self, root: TreeNode) -> List[int]:res = [] #用bfs解题,不是递归,是遍历的思想,bfs是迭代遍历,比较容易if root is None: #bfs先考虑空问题, return resq = Queue()q.put(root)# while 循环控制从上向下一层层遍历while not q.empty():sz = q.qsize()# 记录这一层的最大值levelMax = float('-inf')# for 循环控制每一层从左向右遍历for _ in range(sz):cur = q.get()levelMax = max(levelMax, cur.val)if cur.left is not None:q.put(cur.left)if cur.right is not None:q.put(cur.right)res.append(levelMax)return res
单向队列要从queue import Queue deque 不用,是collections中
题目的特点,和层相关的题目用到bfs会更容易解决
list.index() 方法在 Python 中只返回列表中第一个匹配项的索引。如果列表中有多个相同的值,它只会返回第一个出现的那个值的索引。 结合max使用找到最大值的索引
bfs相关练习题爽多了,都是一个套路出来的,之后在练习分解问题之类的非套路的,先掌握大体流程。
1302. 层数最深叶子节点的和
class Solution:def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:#每一层都累加,返回最后一个就okq = deque([root])level_sum = []while q:sz = len(q)levelsum = 0for i in range(sz): #没想到的思路,q的最后一次遍历就是最后一层,所以最后得到的一个sum就应该是答案cur = q.popleft()levelsum += cur.val if cur.left is not None:q.append(cur.left)if cur.right is not None:q.append(cur.right)level_sum.append(levelsum)return level_sum[-1]
写题目第一步,先想想要初始化哪些东西,要用到的东西要初始化
level = deque() 这样创建的deque,是个空的双端队列。
-sys.maxsize 是 Python 中一个常量,用于表示系统中能够表示的最大整数值的负值。
在 Python 中,sys.maxsize 是 sys 模块中的一个属性,它代表了 Python 中任意整数对象所能表示的最大值。这个值通常用于确定整数类型的范围和容量。sys.maxsize 的值通常是一个非常大的正整数,它实际上是平台相关的,一般情况下是 231 - 1(在 32 位系统上)或者 263 - 1(在 64 位系统上)。
1609. 奇偶树
class Solution:def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:even = True #记录下,一开始是偶数层,#偶数层本应该都是奇数,并且严格递增, 若递减或偶数则不符合 #奇数层本应该都是偶数,并且严格递减 若递增或奇数则不符合q = deque([root])while q:sz = len(q)pre = -sys.maxsize if even else sys.maxsize #一开始给pre赋最小值,怎么样都是递增,给pre赋最大值,怎么样都是递减for i in range(sz):cur = q.popleft()if even:if pre >= cur.val or cur.val % 2 == 0 : return False else:if pre <- cur.val or cur.val % 2 == 1:return False pre = cur.val #经常忘记更新pre!!! if cur.left:q.append(cur.left)if cur.right:q.append(cur.right)even = not even return True
相关文章:

二叉树刷题,bfs刷题
有些题目,你按照拍脑袋的方式去做,可能发现需要在递归代码中调用其他递归函数计算字数的信息。一般来说,出现这种情况时你可以考虑用后序遍历的思维方式来优化算法,利用后序遍历传递子树的信息,避免过高的时间复杂度。…...

为什么要用分布式锁
单应用中,如果要确保多线程修改同一个资源的安全性 加synchronized就可以了 但是性能不高 而mybatis-plus的乐观锁就可以很好的解决这类问题 但是这样的锁机制,只在单应用中有效 试想,在分布式下,有没有可能出现多个应用中的线程同时去修改同一个数据资源的并发问题 例如A …...
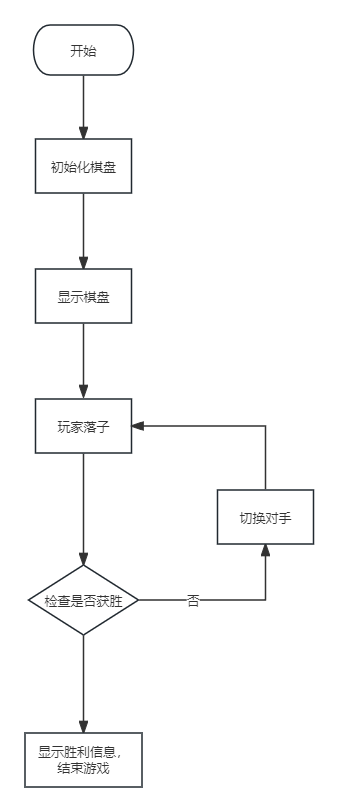
python游戏开发之五子棋游戏制作
五子棋是一种源自中国的传统棋类游戏,起源可以追溯到古代。它是一种两人对弈的游戏,使用棋盘和棋子进行。棋盘通常是一个 1515 的网格,棋子分为黑白两色,双方轮流在棋盘上落子。游戏的目标是通过在棋盘上落子,使自己的…...

文件上传绕过最新版安全狗
本文来源无问社区,更多实战内容,渗透思路可前往查看http://www.wwlib.cn/index.php/artread/artid/9960.html http分块传输绕过 http分块传输⼀直是⼀个很经典的绕过⽅式,只是在近⼏年分块传输⼀直被卡的很死,很多waf都开始加 …...

常用API_2:应用程序编程接口:ArrayList
文章目录 ArrayList常用方法 案例 :上菜 ArrayList 常用方法 来自黑马程序员学习视频 案例 :上菜 待完善...

【Linux操作系统】进程的基本概念(PCB对象)详解
目录 一、进程的基本概念二、进程的描述组织(PCB对象)1.PCB的基本概念2.为什么要有PCB对象(操作系统对进程的组织管理)3.PCB对象的内部属性(tast_struct结构体) 三、查看进程1.ps指令2.top指令3.通过 /proc…...

曙光宁畅中科可控所有服务器机型出厂默认IPMI用户密码
机型 默认IP 用户名/密码 通用 SG机型 DHCP admin/admin 通用 KK机型 DHCP admin/admin 通用 NC 机型 DHCP Admin/Admin5000 I420-G10、I620-G15、I650-G15、I840-GS、I840-G10、I840-G25、I980-G10、A420r-G、A620r-G、A840-G10、TC4600刀片、TC46…...

mysql查线上数据注意数据库的隔离级别
数据库的隔离级别定义了一个事务可能对其他并发事务的可见性,以及它们可能对数据库的影响。隔离级别的选择影响着并发性能和数据的一致性,不同的隔离级别能够防止不同程度的并发问题,如脏读(Dirty Reads)、不可重复读&…...

【专业解析】移动硬盘能识别却打不开:数据恢复实战指南
在数字化时代,移动硬盘作为我们存储重要数据的主要工具之一,其稳定性和安全性直接关系到信息的完整与便捷访问。然而,不少用户会遇到一个令人头疼的问题:移动硬盘能被电脑识别,但尝试打开时却遭遇失败,这往…...

系统 hap
sdk\toolchains\lib\UnsgnedReleasedProfileTemplate.json 各个权限需要的等级 OpenAtom OpenHarmony { "version-name":"2.0.0", "version-code":2, "app-distribution-type":"os_integration", "…...

【Material-UI】按钮与第三方路由库的集成详解
文章目录 一、ButtonBase 组件简介二、与第三方路由库的集成1. React Router示例代码 2. Next.js示例代码 三、客户端导航的优势四、其他自定义集成1. 使用自定义组件示例代码 五、总结 在现代前端开发中,单页应用(SPA)变得越来越普遍。这种应…...

Python获取Excel内容
Python获取Excel内容 目录 Python获取Excel内容1.读取Excel并登陆2.下载Excel中图片 数据存储到列表3.上传到接口 需求:获取xlsx files目录下的所有Excel信息,并将数据打包成字典格式上传到接口 示例数据: 1.读取Excel并登陆 import os impo…...

python实现小游戏随机猜数
1、脚本练习 import random# 初始化剩余的猜测次数 counts 3 # 生成一个1到10之间的随机整数 numb random.randint(1, 10)# 循环直到猜测次数用完 while counts > 0:tmp input("请输入小鱼手里的数字 (你还剩下 {} 次机会): ".format(counts))guess int(tmp)…...

YOLOv5与YOLOv8 训练准备工作(不包含环境搭建)
前言:我发现除了安装环境需要耗费大量时间以外,对于训练前的准备工作也要琢磨一段时间,所以本篇主要讲一下训练前需要准备的工作(主要是XML格式换为txt,以及划分数据集验证集,和训练参数的设置)…...

字节跳动发Seed-TTS语音合成模型,可模仿任意人的声音,效果逼真
前期我们介绍过很多语音合成的模型,比如ChatTTS,微软语音合成大模型等,随着大模型的不断进步,其合成的声音基本跟真人没有多大的区别。本期介绍的是字节跳动自家发布的语音合成模型Seed-TTS。 Seed-TTS 推理包含四个功能模块&…...

微信小程序教程011-3:京西购物商城实战之Home页实现
文章目录 3、首页3.0 创建home分支3.1 配置网络请求3.2 轮播图区域3.2.1 请求轮播图的数据3.2.2 渲染轮播图的UI结构3.2.3 配置小程序分包3.2.4 点击轮播图跳转到商品详情页3.2.5 封装 uni.$showMsg() 方法3.3 分类导航区域3.3.1 获取分类导航的数据3.3.2 渲染分类导航的UI结构…...

使用 Manim 创建一个二维坐标平面【NumberPlane】
NumberPlane 是 Manim 中用于创建一个二维坐标平面的类。它可以帮助用户在场景中可视化坐标轴、网格线以及其他数学概念。具体来说,它的功能包括: 坐标轴:NumberPlane 提供了 x 轴和 y 轴,通常是中心对称的,允许用户清…...
)
Android.mk(TODO)
Android.mk 文件是 Android 构建系统(基于 GNU Make)的一个核心部分,用于定义如何构建项目中的模块。在 Android 中,Android.mk 文件主要用于描述本地模块(如库、可执行文件等)的构建信息。以下是 Android.…...

WPF datagrid 选中某一行后让第一列的checkbox选中
在 WPF 中的 DataGrid 中,如果希望在选中某一行后让该行的第一列中的 CheckBox 选中,可以通过绑定和事件处理来实现。以下是具体的步骤: 绑定数据:确保 DataGrid 的数据源绑定到一个支持 INotifyPropertyChanged 接口的集合。模板…...
(图论:拓扑排序))
洛谷 P1347 排序(福建省历届夏令营)(图论:拓扑排序)
题目描述 一个不同的值的升序排序数列指的是一个从左到右元素依次增大的序列,例如,一个有序的数列 A,B,C,D表示 A<B,B<C,C<D。在这道题中,我们将给你一系列形如 A<B的关系,并要求你判断是否能够根据这些关系确定这个…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
