数理基础知识
数理基础
- 大数定律
- 期望方差
- 常见分布
- 伯努利分布
- 泊松分布
- 高斯分布
- 服从一维高斯分布的随机变量KL散度
- 服从多元高斯分布的随机变量KL散度
- Gibbs不等式
- 凸函数
- Jensen不等式
- 似然函数
- 泰勒近似
- 信息论
- 信息量
- 信息熵
- KL散度
- JS散度
- 交叉熵
- Wiener Process
- SDE
大数定律
期望方差
x为连续随机变量,其概率密度函数为 f x ( x ) f_x(x) fx(x),x的期望值为:
E [ x ] = ∫ − ∞ ∞ x f x ( x ) d x E[x]= \int_{-\infty}^{\infty} xf_x(x)dx E[x]=∫−∞∞xfx(x)dx
g为一个函数,g(x)的期望值为
E [ g ( x ) ] = ∫ − ∞ ∞ g ( x ) f x ( x ) d x E[g(x)] = \int_{-\infty}^{\infty}g(x)f_x(x)dx E[g(x)]=∫−∞∞g(x)fx(x)dx
经常E会有下标,代表了期望值是对应下标分布的随机变量上计算得出的。比如
E x ∼ f x ( x ) [ h ( x , y ) ] = ∫ − ∞ ∞ h ( x , y ) f x ( x ) d x E_{x\sim f_x(x)}[h(x, y)] = \int_{-\infty}^{\infty}h(x, y)f_x(x)dx Ex∼fx(x)[h(x,y)]=∫−∞∞h(x,y)fx(x)dx
常见分布
伯努利分布
又名两点分布或者01分布,是一个离散型概率分布。记其成功概率为 p p p( 0 ≤ p ≤ 1 0\leq p\leq1 0≤p≤1),则:
其概率质量函数为
f x ( x ) = p x ( 1 − p ) 1 − x = { p ( x = 1 ) 1 − p ( x = 0 ) f_x(x)=p^x(1-p)^{1-x}=\left\{ \begin{aligned} p \quad \quad (x= 1) \\ 1-p \quad \quad (x= 0)\\ \end{aligned} \right. fx(x)=px(1−p)1−x={p(x=1)1−p(x=0)
期望为 p p p,方差为 p ( 1 − p ) p(1-p) p(1−p)。
泊松分布
Poisson分布,是一个离散概率分布,适合于描述单位时间内随机事件发生次数的概率分布。
概率质量函数为:
p ( X = k ) = e − λ λ k k ! p(X=k) = \frac{e^{-\lambda}\lambda^k}{k!} p(X=k)=k!e−λλk
期望为 λ \lambda λ, 方差为 λ \sqrt{\lambda} λ。
高斯分布
一维高斯分布:
f x ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f_x(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} fx(x)=2πσ21e−2σ2(x−μ)2
多元高斯分布:
f x ( x ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 e x p [ − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ] f_x(x) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}} exp[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)] fx(x)=(2π)n/2∣Σ∣1/21exp[−21(x−μ)TΣ−1(x−μ)]
μ ∈ R n × 1 \mu \in R^{n\times 1} μ∈Rn×1, Σ ∈ R n × n \Sigma \in R^{n\times n} Σ∈Rn×n, ∣ Σ ∣ |\Sigma| ∣Σ∣为求协方差矩阵的det。
服从一维高斯分布的随机变量KL散度
两个高斯分布 p ( x ) = N ( μ 1 , σ 1 ) p(x)=N(\mu_1, \sigma_1) p(x)=N(μ1,σ1)和 q ( x ) = N ( μ 2 , σ 2 ) q(x)=N(\mu_2, \sigma_2) q(x)=N(μ2,σ2)
D K L ( p , q ) = ∫ p ( x ) l o g p ( x ) q ( x ) d x = ∫ p ( x ) [ l o g p ( x ) − l o g q ( x ) ] d x \begin{aligned} D_{KL}(p, q) &= \int p(x)log\frac{p(x)}{q(x)}dx \\ &= \int p(x)[logp(x) - logq(x)]dx \\ \end{aligned} DKL(p,q)=∫p(x)logq(x)p(x)dx=∫p(x)[logp(x)−logq(x)]dx
∫ p ( x ) l o g p ( x ) d x = ∫ p ( x ) l o g [ 1 2 π σ 1 2 e x p ( − ( x − μ 1 ) 2 2 σ 1 2 ) ] d x = − 1 2 l o g ( 2 π σ 1 2 ) + ∫ p ( x ) ( − ( x − μ 1 ) 2 2 σ 1 2 ) d x = − 1 2 l o g ( 2 π σ 1 2 ) − ∫ p ( x ) x 2 d x − ∫ p ( x ) 2 x μ 1 d x + ∫ p ( x ) μ 1 2 d x 2 σ 1 2 = − 1 2 l o g ( 2 π σ 1 2 ) − μ 1 2 + σ 1 2 − 2 μ 1 2 + μ 1 2 2 σ 1 2 = − 1 2 [ 1 + l o g ( 2 π σ 1 2 ) ] \begin{aligned} \int p(x)logp(x)dx &= \int p(x) log[\frac{1}{\sqrt{2\pi\sigma_1^2}}exp({-\frac{(x-\mu_1)^2}{2\sigma_1^2}})]dx \\ &= -\frac{1}{2}log(2\pi\sigma_1^2) + \int p(x)({-\frac{(x-\mu_1)^2}{2\sigma_1^2}})dx \\ &= -\frac{1}{2}log(2\pi\sigma_1^2) - \frac{\int p(x)x^2dx - \int p(x)2x\mu_1dx + \int p(x)\mu_1^2dx}{2\sigma_1^2} \\ &= -\frac{1}{2}log(2\pi\sigma_1^2) - \frac{\mu_1^2 + \sigma_1^2 - 2\mu_1^2 + \mu_1^2}{2\sigma_1^2} \\ &= -\frac{1}{2}[1 + log(2\pi\sigma_1^2)] \end{aligned} ∫p(x)logp(x)dx=∫p(x)log[2πσ121exp(−2σ12(x−μ1)2)]dx=−21log(2πσ12)+∫p(x)(−2σ12(x−μ1)2)dx=−21log(2πσ12)−2σ12∫p(x)x2dx−∫p(x)2xμ1dx+∫p(x)μ12dx=−21log(2πσ12)−2σ12μ12+σ12−2μ12+μ12=−21[1+log(2πσ12)]
∫ p ( x ) l o g q ( x ) d x = ∫ p ( x ) l o g [ 1 2 π σ 2 2 e x p ( − ( x − μ 2 ) 2 2 σ 2 2 ) ] d x = − 1 2 l o g ( 2 π σ 2 2 ) + ∫ p ( x ) ( − ( x − μ 2 ) 2 2 σ 2 2 ) d x = − 1 2 l o g ( 2 π σ 2 2 ) − ∫ p ( x ) x 2 d x − ∫ p ( x ) 2 x μ 2 d x + ∫ p ( x ) μ 2 2 d x 2 σ 2 2 = − 1 2 l o g ( 2 π σ 2 2 ) − μ 1 2 + σ 1 2 − 2 μ 1 μ 2 + μ 2 2 2 σ 2 2 = − 1 2 l o g ( 2 π σ 2 2 ) − σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 \begin{aligned} \int p(x)logq(x)dx &= \int p(x) log[\frac{1}{\sqrt{2\pi\sigma_2^2}}exp({-\frac{(x-\mu_2)^2}{2\sigma_2^2}})]dx \\ &= -\frac{1}{2}log(2\pi\sigma_2^2) + \int p(x)({-\frac{(x-\mu_2)^2}{2\sigma_2^2}})dx \\ &= -\frac{1}{2}log(2\pi\sigma_2^2) - \frac{\int p(x)x^2dx - \int p(x)2x\mu_2dx + \int p(x)\mu_2^2dx}{2\sigma_2^2} \\ &= -\frac{1}{2}log(2\pi\sigma_2^2) - \frac{\mu_1^2 + \sigma_1^2 - 2\mu_1\mu_2 + \mu_2^2}{2\sigma_2^2} \\ &= -\frac{1}{2}log(2\pi\sigma_2^2) - \frac{ \sigma_1^2 + (\mu_1 - \mu_2)^2}{2\sigma_2^2} \\ \end{aligned} ∫p(x)logq(x)dx=∫p(x)log[2πσ221exp(−2σ22(x−μ2)2)]dx=−21log(2πσ22)+∫p(x)(−2σ22(x−μ2)2)dx=−21log(2πσ22)−2σ22∫p(x)x2dx−∫p(x)2xμ2dx+∫p(x)μ22dx=−21log(2πσ22)−2σ22μ12+σ12−2μ1μ2+μ22=−21log(2πσ22)−2σ22σ12+(μ1−μ2)2
带入可得:
D K L ( p , q ) = ∫ p ( x ) [ l o g p ( x ) − l o g q ( x ) ] d x = − 1 2 [ 1 + l o g ( 2 π σ 1 2 ) ] + 1 2 l o g ( 2 π σ 2 2 ) + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 = l o g ( σ 2 σ 1 ) + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 \begin{aligned} D_{KL}(p, q) &= \int p(x)[logp(x) - logq(x)]dx \\ &= -\frac{1}{2}[1 + log(2\pi\sigma_1^2)] + \frac{1}{2}log(2\pi\sigma_2^2) + \frac{ \sigma_1^2 + (\mu_1 - \mu_2)^2}{2\sigma_2^2} \\ &= log(\frac{\sigma_2}{\sigma_1}) + \frac{\sigma_1^2 + (\mu_1-\mu_2)^2}{2\sigma_2^2} - \frac{1}{2} \end{aligned} DKL(p,q)=∫p(x)[logp(x)−logq(x)]dx=−21[1+log(2πσ12)]+21log(2πσ22)+2σ22σ12+(μ1−μ2)2=log(σ1σ2)+2σ22σ12+(μ1−μ2)2−21
服从多元高斯分布的随机变量KL散度
与一元高斯分布类似,第一部分:
∫ p ( x ) l o g p ( x ) d x = ∫ p ( x ) l o g [ 1 ( 2 π ) n / 2 ∣ Σ 1 ∣ 1 / 2 e x p [ − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] ] d x = l o g 1 ( 2 π ) n / 2 ∣ Σ 1 ∣ 1 / 2 + ∫ p ( x ) [ − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] d x = l o g 1 ( 2 π ) n / 2 ∣ Σ 1 ∣ 1 / 2 − 1 2 E x ∼ p ( x ) [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] \begin{aligned} \int p(x)logp(x)dx &= \int p(x) log[\frac{1}{(2\pi)^{n/2}|\Sigma_1|^{1/2}} exp[-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)]] dx\\ &= log\frac{1}{(2\pi)^{n/2}|\Sigma_1|^{1/2}} + \int p(x) [-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)]dx\\ &= log\frac{1}{(2\pi)^{n/2}|\Sigma_1|^{1/2}} -\frac{1}{2}E_{x\sim p(x)}[(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)] \end{aligned} ∫p(x)logp(x)dx=∫p(x)log[(2π)n/2∣Σ1∣1/21exp[−21(x−μ1)TΣ1−1(x−μ1)]]dx=log(2π)n/2∣Σ1∣1/21+∫p(x)[−21(x−μ1)TΣ1−1(x−μ1)]dx=log(2π)n/2∣Σ1∣1/21−21Ex∼p(x)[(x−μ1)TΣ1−1(x−μ1)]
第二部分同理可得:
∫ p ( x ) l o g q ( x ) d x = l o g 1 ( 2 π ) n / 2 ∣ Σ 2 ∣ 1 / 2 − 1 2 E x ∼ p ( x ) [ ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ] \begin{aligned} \int p(x)logq(x)dx &= log\frac{1}{(2\pi)^{n/2}|\Sigma_2|^{1/2}} -\frac{1}{2}E_{x\sim p(x)}[(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2)]\\ \end{aligned} ∫p(x)logq(x)dx=log(2π)n/2∣Σ2∣1/21−21Ex∼p(x)[(x−μ2)TΣ2−1(x−μ2)]
带入可得:
D K L ( p , q ) = ∫ p ( x ) [ l o g p ( x ) − l o g q ( x ) ] d x = 1 2 l o g ∣ Σ 2 ∣ ∣ Σ 1 ∣ + 1 2 E x ∼ p ( x ) [ ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] \begin{aligned} D_{KL}(p, q) &= \int p(x)[logp(x) - logq(x)]dx \\ &= \frac{1}{2}log\frac{|\Sigma_2|}{|\Sigma_1|} + \frac{1}{2}E_{x\sim p(x)} [(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2) - (x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)] \end{aligned} DKL(p,q)=∫p(x)[logp(x)−logq(x)]dx=21log∣Σ1∣∣Σ2∣+21Ex∼p(x)[(x−μ2)TΣ2−1(x−μ2)−(x−μ1)TΣ1−1(x−μ1)]
多元正态分布下期望矩阵化的表示结果:
E [ x T A x ] = t r ( A Σ ) + μ T A μ E[x^TAx] = tr(A\Sigma) + \mu^TA\mu E[xTAx]=tr(AΣ)+μTAμ
证明过程如下:
E [ x T A x ] = E [ t r ( x T A x ) ] = E [ t r ( A x x T ) ] = t r [ E ( A x x T ) ] = t r [ A ⋅ E ( x x T ) ] = t r [ A ( Σ + μ μ T ) ] = t r ( A Σ ) + t r ( A μ μ T ) = t r ( A Σ ) + t r ( μ T A μ ) = t r ( A Σ ) + μ T A μ \begin{aligned} E[x^TAx] = E[tr(x^TAx)] = E[tr(Axx^T)] = tr[E(Axx^T)] &= tr[A\cdot E(xx^T)] \\ &= tr[A(\Sigma + \mu\mu^T)] \\ &= tr(A\Sigma) + tr(A\mu\mu^T) \\ &= tr(A\Sigma) + tr(\mu^TA\mu) \\ & = tr(A\Sigma) + \mu^TA\mu \end{aligned} E[xTAx]=E[tr(xTAx)]=E[tr(AxxT)]=tr[E(AxxT)]=tr[A⋅E(xxT)]=tr[A(Σ+μμT)]=tr(AΣ)+tr(AμμT)=tr(AΣ)+tr(μTAμ)=tr(AΣ)+μTAμ
整个证明过程用到了如下性质:
- x T A x x^TAx xTAx是个标量,因此 x T A x = t r ( x T A x ) = t r ( A x x T ) x^TAx=tr(x^TAx)=tr(Axx^T) xTAx=tr(xTAx)=tr(AxxT)
- Σ = E [ ( x − μ ) ( x − μ ) T ] = E [ x x T − x μ T − μ x T − μ μ T ] = E ( x x T ) − μ μ T \Sigma=E[(x-\mu)(x-\mu)^T] = E[xx^T-x\mu^T-\mu x^T-\mu\mu^T]=E(xx^T)-\mu\mu^T Σ=E[(x−μ)(x−μ)T]=E[xxT−xμT−μxT−μμT]=E(xxT)−μμT
进一步带入可得:
D K L ( p , q ) = 1 2 l o g ∣ Σ 2 ∣ ∣ Σ 1 ∣ + 1 2 E x ∼ p ( x ) [ ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] = 1 2 l o g ∣ Σ 2 ∣ ∣ Σ 1 ∣ + 1 2 t r ( Σ 2 − 1 Σ 1 ) + ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) T − 1 2 t r ( Σ 1 − 1 Σ 1 ) − ( μ 1 − μ 1 ) T Σ 2 − 1 ( μ 1 − μ 1 ) T = 1 2 l o g ∣ Σ 2 ∣ ∣ Σ 1 ∣ + 1 2 t r ( Σ 2 − 1 Σ 1 ) + ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) T − 1 2 n \begin{aligned} D_{KL}(p, q) &= \frac{1}{2}log\frac{|\Sigma_2|}{|\Sigma_1|} + \frac{1}{2}E_{x\sim p(x)} [(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2) - (x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)]\\ &= \frac{1}{2}log\frac{|\Sigma_2|}{|\Sigma_1|} + \frac{1}{2}tr(\Sigma_2^{-1}\Sigma_1) + (\mu_1 - \mu_2)^T\Sigma_2^{-1}(\mu_1-\mu_2)^T - \frac{1}{2}tr(\Sigma_1^{-1}\Sigma_1) - (\mu_1-\mu_1)^T\Sigma_2^{-1}(\mu_1-\mu_1)^T \\ &= \frac{1}{2}log\frac{|\Sigma_2|}{|\Sigma_1|} + \frac{1}{2}tr(\Sigma_2^{-1}\Sigma_1) + (\mu_1 - \mu_2)^T\Sigma_2^{-1}(\mu_1-\mu_2)^T -\frac{1}{2}n \end{aligned} DKL(p,q)=21log∣Σ1∣∣Σ2∣+21Ex∼p(x)[(x−μ2)TΣ2−1(x−μ2)−(x−μ1)TΣ1−1(x−μ1)]=21log∣Σ1∣∣Σ2∣+21tr(Σ2−1Σ1)+(μ1−μ2)TΣ2−1(μ1−μ2)T−21tr(Σ1−1Σ1)−(μ1−μ1)TΣ2−1(μ1−μ1)T=21log∣Σ1∣∣Σ2∣+21tr(Σ2−1Σ1)+(μ1−μ2)TΣ2−1(μ1−μ2)T−21n
进一步延伸到VAE的训练过程,假设 p ( x ) = N ( μ 1 , σ 1 ) p(x)=N(\mu_1, \sigma_1) p(x)=N(μ1,σ1)为encoder估计出的隐变量 z z z概率分布的参数, q ( x ) = N ( μ 2 , σ 2 ) = ( 0 , I ) q(x)=N(\mu_2, \sigma_2)=(0, I) q(x)=N(μ2,σ2)=(0,I)为隐变量 z z z的先验分布。我们希望对学习到的隐变量分布进行约束,使其符合标准高斯分布,方便后续采样生成。则有:
K L ( p , q ) = K L ( N ( μ 1 , σ 1 ) , N ( 0 , I ) ) = − l o g σ 1 + 1 2 ( σ 1 2 + μ 1 2 ) − 1 2 KL(p, q) = KL(N(\mu_1, \sigma_1), N(0, I)) = -log\sigma_1 + \frac{1}{2}(\sigma_1^2 + \mu_1^2) - \frac{1}{2} KL(p,q)=KL(N(μ1,σ1),N(0,I))=−logσ1+21(σ12+μ12)−21
Gibbs不等式
若 ∑ i = 1 n p i = ∑ i = 1 n q i = 1 \sum_{i=1}^np_i=\sum_{i=1}^nq_i=1 ∑i=1npi=∑i=1nqi=1,且 p i , q i ∈ ( 0 , 1 ] p_i, q_i \in (0, 1] pi,qi∈(0,1],则有:
− ∑ i n p i l o g p i ≤ − ∑ i n p i l o g q i -\sum_i^np_ilogp_i\leq -\sum_i^n p_ilogq_i −i∑npilogpi≤−i∑npilogqi
当且仅当 p i = q i , ∀ i p_i=q_i, \forall i pi=qi,∀i时,等号成立。
凸函数
convex function,是指函数图形上,任意两点连成的线段,皆位于图形的上方的实值函数。如单变的二次函数和指数函数。快速判断就是函数图形开口向上。
Jensen不等式
如果x是随机变量,f是凸函数,则有如下性质,称之为Jensen’s inequality(詹森不等式/琴生不等式)。
f ( E ( x ) ) ≤ E [ f ( x ) ] f(E(x)) \leq E[f(x)] f(E(x))≤E[f(x)]
ELBO证明中会用到对数似然,这里延伸下log(x)函数是凹函数,-log(x)是凸函数。则有:
l o g ( E ( x ) ) ≥ E [ l o g ( x ) ] log(E(x)) \geq E[log(x)] log(E(x))≥E[log(x)]
似然函数
likelihood function,译为似然函数。是一种关于统计模型中参数的函数,表示模型参数的似然性。假设随机变量x的概率密度函数为 f ( x ∣ θ ) f(x|\theta) f(x∣θ),样本集D上有m个样本,则D上的似然函数写作 L ( θ ∣ x ) = ∏ i m f ( x i ∣ θ ) L(\theta|x)= \prod_i^mf(x_i|\theta) L(θ∣x)=∏imf(xi∣θ)。
为什么要用对数似然?
- 对 p ( x ) p(x) p(x)取对数不影响单调性。
- 减少计算量。似然函数是每个数据点概率的连乘。取对数可以将连乘化为连加,同时如果概率分布中含有指数项,比如高斯分布,也能将指数项化为求和形式,进一步减少计算量。
- 利于结果更好的计算。因为概率在[0, 1]之间,因此概率连乘会变为一个很小的值,甚至可能会引起浮点数下溢,尤其是当数据集很大时,联合概率趋向于0,非常不利于计算。
泰勒近似
泰勒公式:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . + f n ( x 0 ) n ! ( x − x 0 ) n + o ( ( x − x 0 ) n ) f(x) = f(x_0) + f^{'}(x_0)(x-x_0) + \frac{f^{''}(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^{n}(x_0)}{n!}(x-x_0)^n + o((x-x_0)^n) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n+o((x−x0)n)
麦克劳林公式(泰勒公式的特殊形式,在零点展开):
f ( x ) = f ( 0 ) + f ′ ( 0 ) ( x ) + f ′ ′ ( 0 ) 2 ! x 2 + . . . + f n ( 0 ) n ! x n + o ( x n ) f(x) = f(0) + f^{'}(0)(x) + \frac{f^{''}(0)}{2!}x^2 + ... + \frac{f^{n}(0)}{n!}x^n + o(x^n) f(x)=f(0)+f′(0)(x)+2!f′′(0)x2+...+n!fn(0)xn+o(xn)
常见函数的麦克劳林展开:
e x = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + o ( x 3 ) e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + o(x^3) ex=1+x+2!1x2+3!1x3+o(x3)
l n ( 1 + x ) = x − 1 2 ! x 2 + 1 3 ! x 3 + o ( x 3 ) ln(1+x) = x - \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + o(x^3) ln(1+x)=x−2!1x2+3!1x3+o(x3)
s i n ( x ) = x − 1 3 ! x 3 + 1 5 ! x 5 + o ( x 5 ) sin(x) = x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 + o(x^5) sin(x)=x−3!1x3+5!1x5+o(x5)
c o s ( x ) = x − 1 2 ! x 2 + 1 4 ! x 4 + o ( x 4 ) cos(x) = x - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 + o(x^4) cos(x)=x−2!1x2+4!1x4+o(x4)
( 1 + x ) α = 1 + α 1 ! x + α ( α − 1 ) 2 ! x 2 + α ( α − 1 ) ( α − 2 ) 3 ! x 3 + o ( x 3 ) (1+x)^{\alpha} = 1 + \frac{\alpha}{1!}x + \frac{\alpha(\alpha-1)}{2!}x^2 + \frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3 + o(x^3) (1+x)α=1+1!αx+2!α(α−1)x2+3!α(α−1)(α−2)x3+o(x3)
正常近似取到一阶或者二阶项即可。
信息论
信息量
− l o g ( p ( X = x ) ) -log(p(X=x)) −log(p(X=x))表示一个概率事件或者随机变量X取值x时的信息量。 p ( X = x ) p(X=x) p(X=x)为取值为x的概率。
信息量的单位随着计算公式中 l o g log log运算的底数而变化, l o g log log底数为2时单位为比特(bit),log底数为e时,单位为奈特(nat)。
信息熵
信息熵就是期望信息量,即对于一个信号系统来说,对于每次的信号,在平均意义上为了编码这个信号需要使用的信息量。在一个信号系统中,信息熵最大的时候是当每个信号概率相等的时候。通过大数定律可知,信息熵是编码一个信号系统所需信息量多理论下界。
h ( x ) = − ∑ x ∈ X p ( x ) l o g p ( x ) h(x) = - \sum_{x\in X} p(x)logp(x) h(x)=−x∈X∑p(x)logp(x)
KL散度
全名Kullback-Leible散度,又称相对熵。用以衡量两个分布之间的距离, D K L ( p , q ) D_{KL}(p, q) DKL(p,q)表示真实分布为 p p p时,度量近似分布 q q q和真实分布之间的差异程度。
连续随机变量的KL散度:
D K L ( p ∣ ∣ q ) = E x ∼ p [ l o g p ( x ) q ( x ) ] = ∫ p ( x ) l o g p ( x ) q ( x ) d x D_{KL}(p||q) = E_{x\sim p}[log\frac{p(x)}{q(x)}]=\int p(x)log\frac{p(x)}{q(x)} dx DKL(p∣∣q)=Ex∼p[logq(x)p(x)]=∫p(x)logq(x)p(x)dx
离散随机变量的KL散度:
D K L ( p ∣ ∣ q ) = E x ∼ p [ l o g p ( x ) q ( x ) ] = ∑ x ∈ X p ( x ) l o g p ( x ) q ( x ) D_{KL}(p||q) = E_{x\sim p}[log\frac{p(x)}{q(x)}]=\sum_{x\in X}p(x)log\frac{p(x)}{q(x)} DKL(p∣∣q)=Ex∼p[logq(x)p(x)]=x∈X∑p(x)logq(x)p(x)
KL散度有如下特性:
- 不对称性: D K L ( p ∣ ∣ q ) ≠ D K L ( q ∣ ∣ p ) D_{KL}(p||q) \neq D_{KL}(q||p) DKL(p∣∣q)=DKL(q∣∣p)。
- 非负性: D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q)\geq0 DKL(p∣∣q)≥0。
JS散度
Jensen-Shanno散度,是对称的。
交叉熵
交叉熵定义如下:
H ( p , q ) = E x ∼ p [ − l o g q ( x ) ] H(p, q) = E_{x\sim p}[-logq(x)] H(p,q)=Ex∼p[−logq(x)]
离散随机变量的交叉熵形式如下:
H ( p , q ) = E x ∼ p [ − l o g q ( x ) ] = − ∑ x ∈ X p ( x ) l o g q ( x ) H(p, q) = E_{x\sim p}[-logq(x)] = -\sum_{x\in X}p(x)logq(x) H(p,q)=Ex∼p[−logq(x)]=−x∈X∑p(x)logq(x)
连续随机变量的交叉熵形式如下:
H ( p , q ) = E x ∼ p [ − l o g q ( x ) ] = ∫ p ( x ) l o g q ( x ) d x H(p, q) = E_{x\sim p}[-logq(x)] = \int p(x)logq(x)dx H(p,q)=Ex∼p[−logq(x)]=∫p(x)logq(x)dx
交叉熵可由相对熵推导得到:
D K L ( p ∣ ∣ q ) = E x ∼ p [ l o g p ( x ) q ( x ) ] = ∑ x ∈ X p ( x ) l o g p ( x ) q ( x ) = ∑ x ∈ X p ( x ) l o g p ( x ) − ∑ x ∈ X p ( x ) l o g q ( x ) = − H ( p ) + H ( p , q ) \begin{aligned} D_{KL}(p||q) = E_{x\sim p}[log\frac{p(x)}{q(x)}]&=\sum_{x\in X}p(x)log\frac{p(x)}{q(x)} \\ &=\sum_{x\in X}p(x)logp(x) - \sum_{x\in X}p(x)logq(x) \\ &=-H(p) + H(p, q) \end{aligned} DKL(p∣∣q)=Ex∼p[logq(x)p(x)]=x∈X∑p(x)logq(x)p(x)=x∈X∑p(x)logp(x)−x∈X∑p(x)logq(x)=−H(p)+H(p,q)
H ( p ) H(p) H(p)为真实分布的信息熵,不影响模型参数优化。因此模型优化过程中,可以直接用交叉熵 H ( p , q H(p, q H(p,q作为目标函数。
对于交叉熵,可以有个直观的解释:数据集服从真实分布 p p p,从数据集中抽取样本 x x x,该样本被抽到的概率为 p ( x ) p(x) p(x),如果用近似分布 q q q去编码该样本,需要用到的信息量为 − l o g q ( x ) -logq(x) −logq(x)。对整个数据集求期望,当近似分布的参数优化至 H ( p , q ) = H ( p ) H(p, q)=H(p) H(p,q)=H(p)时,可以认为近似分布 q ( x ) q(x) q(x)已优化至和真实分布 p ( x ) p(x) p(x)一致。
Wiener Process
维纳过程,又称为布朗运动,它是一种连续时间,连续状态的独立增量过程,其增量服从正态分布 N ∼ ( 0 , Δ t ) N\sim(0, \Delta t) N∼(0,Δt)。可以用以下公式来表示维纳过程:
W ( t ) = t Z W(t) = \sqrt{t} Z W(t)=tZ
其中 Z Z Z是一个标准正态分布随机变量,t表示时间。对于维纳过程,我们可以证明其具有如下性质:
- W ( 0 ) W(0) W(0) = 0。
- W ( t ) W(t) W(t)是一个连续的随机变量。
- W ( t ) W(t) W(t)具有独立增量:对于任意 0 ≤ t 1 < t 2 < . . . < t n 0\leq t_1 < t_2 <...<t_n 0≤t1<t2<...<tn,其增量 W ( t i + 1 ) W(t_{i+1}) W(ti+1) - W ( t i ) W(t_{i}) W(ti)相互独立。
- 增量服从正态分布:对于任意 0 ≤ s < t 0\leq s < t 0≤s<t,其增量 W ( t ) W(t) W(t) - W ( s ) W(s) W(s)服从 N ∼ ( 0 , t − s ) N\sim(0, t-s) N∼(0,t−s)的正态分布。
SDE
Applied Stochastic Differential Equations
随机微分方程最泛化的表达形式:
d x = f ( x , t ) d t + L ( x , t ) d w dx = f(x, t)dt + L(x, t)dw dx=f(x,t)dt+L(x,t)dw
f ( x , t ) f(x, t) f(x,t)为drift函数,决定了系统的nominal dynamics, L ( x , t ) L(x, t) L(x,t)是扩散矩阵,决定了噪声如何进入系统。 w w w为布朗运动。
其均值和方差可表示为:
d m d t = E [ f ( x , t ) ] \frac{dm}{dt} = E[f(x, t)] dtdm=E[f(x,t)]
d P d t = E [ f ( x , t ) ( x − m ) T ] + E [ ( x − m ) f T ( x , t ) ] + E [ L ( x , t ) Q L T ( x , t ) ] \frac{dP}{dt} = E[f(x, t)(x-m)^T] + E[(x-m)f^T(x, t)] + E[L(x, t)QL^T(x, t)] dtdP=E[f(x,t)(x−m)T]+E[(x−m)fT(x,t)]+E[L(x,t)QLT(x,t)]
具体可见上书的公式5.51。
相关文章:

数理基础知识
数理基础 大数定律期望方差常见分布伯努利分布泊松分布高斯分布服从一维高斯分布的随机变量KL散度服从多元高斯分布的随机变量KL散度 Gibbs不等式凸函数Jensen不等式 似然函数泰勒近似信息论信息量信息熵KL散度JS散度交叉熵 Wiener ProcessSDE 大数定律 期望方差 x为连续随机…...

Java解决lombok和mapstruct编译模块的问题
pom.xml <dependencies><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><!-- 1.18.16版本 --><version>${lombok.version}</version><scope>provided</scope><!-- 防…...

大模型场景应用全集:持续更新中
一、应用场景 1.办公场景 智能办公:文案生成(协助构建大纲优化表达内容生成)、PPT美化(自动排版演讲备注生成PPT)、数据分析(生成公式数据处理表格生成)。 智能会议:会议策划&…...
)
理解RabbitMQ中的消息存储机制:非持久化、持久化与惰性队列(Lazy Queue)
文章目录 1. 非持久化消息(Transient Messages)内存压力处理 2. 持久化消息(Persistent Messages)3. 惰性队列(Lazy Queue)官方推荐 总结 在RabbitMQ中,消息的存储和处理方式可以根据不同的需求…...

【机器学习】BP神经网络正向计算
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 BP神经网络正向计算1. 引言2. BP神经网络结构回顾3. 正向计算的基本原理4. 数学…...

谷粒商城实战笔记-108~109-elasticsearch删除与批量导入
一,108-全文检索-ElasticSearch-入门-put&post修改数据 第一种更新方式: POST customer/external/1/_update {"doc":{"name": "John Doew"} }第二种更新方式: POST customer/external/1 { "name&q…...

RabbitMQ:发送者的可靠性之使用消息确认回调
文章目录 配置RabbitMQ的ConfirmCallback使用ConfirmCallback发送消息实际使用中的注意事项总结 在开发消息驱动的系统时,消息的可靠传递至关重要。而RabbitMQ作为一个广泛使用的消息队列中间件,提供了多种消息确认机制,确保消息从生产者到交…...

HCIP学习 | OSPF---LSA限制、不规则区域、附录E、选路
目录 Days06(24.8.8)OSPF---LSA限制、不规则区域、附录E、选路 特殊区域 stub 区域, 末节区域 Totally stub :完全的末节区域 NSSA区域:(not so stub area) 非完全末节区域 完全的非完全的末节区域: …...
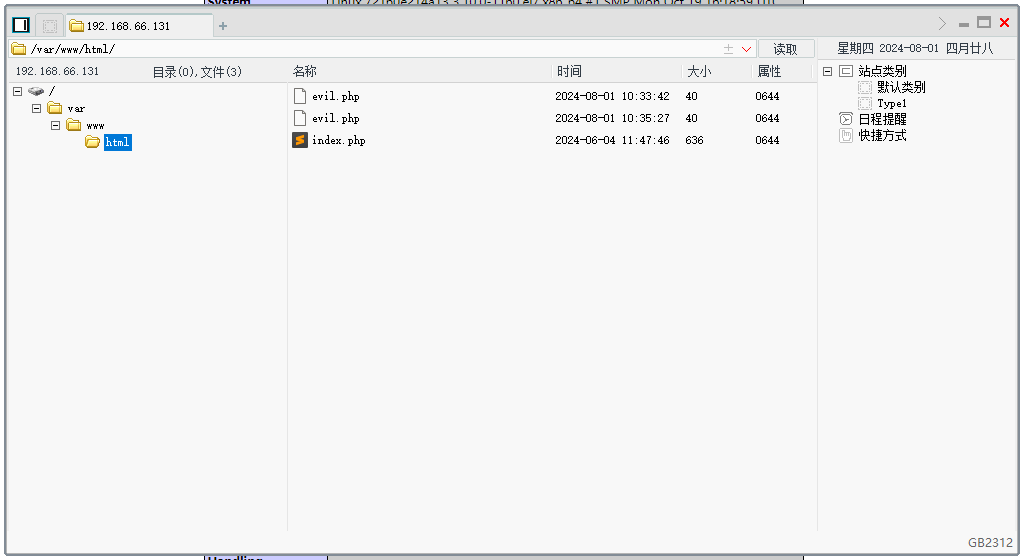
CVE-2017-15715~Apache解析漏洞【春秋云境靶场渗透】
Apache解析漏洞 漏洞原理 # Apache HTTPD 支持一个文件拥有多个后缀,并为不同后缀执行不同的指令。比如如下配置文件: AddType text/html .html AddLanguage zh-CN .cn# 其给 .html 后缀增加了 media-type ,值为 text/html ;给 …...

thinkphp 5.0.24生成模块
访问的形式生成模块: 1、需要在入口文件Public/index.php中加入以下代码: //生成Home模块,添加以下这句后,打开浏览器执行:http://www3.phptp5.com/public/index.php自动生成Home模块 \think\Build::module(Home); …...

值得注意!家里有带毛发动物就有浮毛?宠物空气净化器一键净化
上次跟朋友逛完街去她家,她家热情的哈基米开门就一个猛冲,我朋友接住就是一顿猛亲,亲猫一时爽,汗液粘着猫毛,粘得满手臂、满脸都是,看得鼻炎星人头皮发麻...好多养宠物的都说,梳毛根本不管用&am…...
设置)
Linux 代理(proxy)设置
有关网络代理的环境变量 环境变量说明可选的取值http_proxyhttp协议的网络连接使用该代理。ip:porthttp://ip:portsocks://ip:portsocks4://ip:portsocks5://ip:porthttps_proxyhttps协议的网络连接使用该代理。ftp_proxyftp协议使用该代理。all_proxy所有网络协议的网络连接都…...

操作系统真相还原:获取文件属性
14.15 获得文件属性 14.15.1 ls命令的幕后功臣 ls 命令中调用了大量的系统调用 stat64 和write ,其中stat64 用于获得文件的属性信息, write 用于把信息输出到屏幕,即标准输出。这里的 stat64 表示 64 位版本的 stat。 其函数原型是int sta…...

聚鼎装饰画:投资一家装饰画店铺要花费多少钱
在艺术的殿堂里,每一幅装饰画都是静默的诗篇,而开设一家装饰画店铺,便是将这份静谧与美好呈现给世界的开始。然而,背后的投资成本,却是一笔需要精打细算的账。 店铺的选址,犹如画家挑选画布,至关…...

编程的魅力、其重要性、学习方法以及未来趋势
在数字化时代,编程已不仅仅是程序员的专属技能,它逐渐渗透到我们生活的方方面面,成为连接现实与虚拟世界的桥梁。从日常使用的智能手机应用到探索宇宙奥秘的超级计算机,编程的力量无处不在。本文将深入探讨编程的魅力、其重要性、…...

ubuntu init set
1 cuda驱动 cuda use not open test 自己下载安装 以上操作后可能是核显卡,需要执行下列进入独立显卡,才能进行HDMI链接 sudo prime-select nvidia sudo prime-select intel prime-select query 该命令用于查看目前的显卡使用模式,可以看到…...

MySQL数据分析进阶(八)存储过程
※食用指南:文章内容为‘CodeWithMosh’SQL进阶教程系列学习笔记,笔记整理比较粗糙,主要目的自存为主,记录完整的学习过程。(图片超级多,慎看!) 【中字】SQL进阶教程 | 史上最易懂S…...

最深的根,
1498. 最深的根 题目 提交记录 讨论 题解 视频讲解 一个无环连通图可以被视作一个树。 树的高度取决于所选取的根节点。 现在,你要找到可以使得树的高度最大的根节点。 它被称为最深的根。 输入格式 第一行包含整数 NN,表示节点数量。 节点…...

【常见的设计模式】工厂模式
【设计模式专题之工厂方法模式】2.积木工厂 题目描述 小明家有两个工厂,一个用于生产圆形积木,一个用于生产方形积木,请你帮他设计一个积木工厂系统,记录积木生产的信息。 输入描述 输入的第一行是一个整数 N(1 …...

postgres收缩工具两种工具的使用对比
postgres收缩工具安装和使用 第一章 需要使用插件处理膨胀的原因 Postgresql通过数据多版本实现MVCC,现象是删除数据并不会真正删除数据,而是修改标识,更新是通过删除+插入的方式进行,所以在频繁更新的OLTP系统,会造成数据膨胀。 PG数据库本身有处理膨胀问题的vacuum工…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
