聚焦光热型太阳光模拟器助力多晶硅均匀加热

晶圆均匀加热技术综述

晶圆均匀加热是半导体制造过程中的关键技术之一，直接影响着晶圆上各种加工工艺的质量和稳定性。晶圆加热的目的在于化学气相沉积、退火、氧化等工艺中，通过对晶圆进行必要的热处理，以促进或优化后续工艺步骤。不均匀的温度分布可能导致器件性能差异，影响产品的质量。因此，如何实现晶圆均匀加热是半导体制造技术中的重要课题。

 

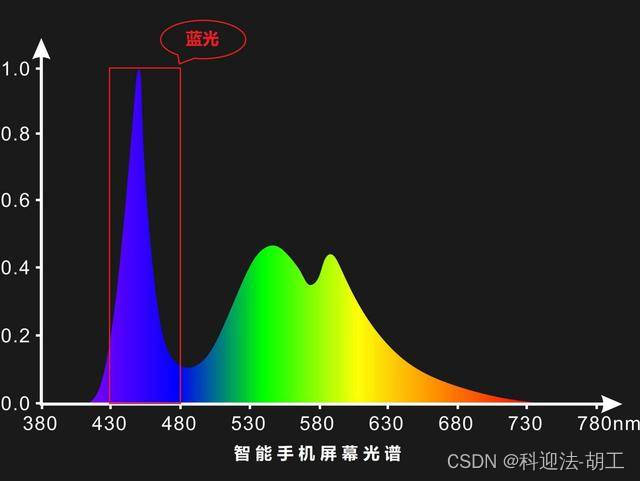
晶圆均匀加热的关键技术

晶圆均匀加热的关键技术主要包括以下几个方面：

加热方式的选择：传统的加热方式如辐射加热或炉内加热存在热分布不均的问题。相比之下，激光加热和高频感应加热因其加热速度快、温度控制精准而被广泛研究。

• 温度控制技术：精确的温度控制对于保证晶圆加热均匀性至关重要。这涉及到温度传感器的选择、温度监测与反馈系统的建立以及先进的温度控制算法的实施。
• 加热设备的优化：加热设备的优化包括热源的设计、加热时间的控制以及加热环境的调节等。例如，激光退火设备可通过优化激光器阵列组件来提高加热均匀性。

加热过程中的监控与调整：在加热过程中，通过实时监控晶圆的温度分布，及时调整加热参数，以确保加热均匀性。

 

晶圆均匀加热的实际应用

晶圆均匀加热技术在实际应用中，如快速热退火（Rapid Thermal Annealing, RTA）和激光退火（Laser Annealing），已被证明可以显著提高生产效率和产品质量。特别是在功率器件和先进制程芯片领域，激光退火技术已成为主要的退火方案。

 

 

结论

综上所述，晶圆均匀加热技术在半导体制造中占有举足轻重的地位。通过不断的研究和技术革新，已经涌现出多种有效的加热方法，如激光加热和RTA等。这些技术的发展不仅提高了晶圆加热的均匀性，也为半导体器件的性能提升提供了有力保障。未来，随着技术的不断进步，晶圆均匀加热技术将进一步推动半导体制造工艺向前发展。