状态压缩动态规划——状压dp
状压dp:意思是将状态进行压缩,从而更容易地写出状态转移方程
通常做法:将每个状态(一个集合)用二进制表示,每个位的1就代表着这个编号的元素存在,0就代表着这个编号的元素不存在,如二进制100110,即是集合{1,2,5}的压缩
通过状态压缩,我们可以使得状态通过位运算来判断是否可以转移
如:
一、
假设棋盘要放置k个国王,国王对其周围八个格子都可发动进攻,如果要求这一行与上一行的国王不能相互进攻
那么设上一行的状态为x(二进制数),这一行的状态为y的话,由于这一行放的国王的左上角,正上方,右上角都不能出现上一行的国王
所以:
正上方不出现上一行的国王的条件为:x&y==false
左上角不出现上一行的国王的条件为:x&(y<<1)==false
右上角不出现上一行的国王的条件为:x&(y>>1)==false
通过简单的位运算判断,对于每一个y,我们都可以枚举所有x,并可以快速找出能够转移到y的合法的x的状态,从而使状态转移变得简单
因此,对于这种题目,我们通常需要预处理出所有的x状态,以方便我们进行枚举
题目链接:#2153. 「SCOI2005」互不侵犯 - 题目 - LibreOJ (loj.ac)
实现代码:
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
int n,K;
int sti[600],sta[600],cnt;
//sti[i]:第i种状态压缩
//sta[i]: 第i种状态放的国王的数量
//cnt:状态总数
long long f[10][85][600];
//状态转移方程:
//f[i][l][j]:摆到第i行,已经摆了l个,而且第i行的摆法是j状态,总共有多少种方法数
//所以:
//f[i][l][j]=sigma f[i-1][l-sta[j]][x] 枚举所有合法的x//预处理所有状态
void dfs(int x,int num,int cur){if(cur>=n){sti[++cnt]=x;sta[cnt]=num;return;}dfs(x|(1<<cur),num+1,cur+2);//cur所指的位置放棋子,那么由于国王会进攻隔壁的棋子,所以cur+2才是到下一个能放棋子的位置dfs(x,num,cur+1);//cur所指的位置不放棋子,则遍历到下一个位置即可
}
int main(){cin>>n>>K;dfs(0,0,0);//先初始化第一行for(int i=1;i<=cnt;i++) f[1][sta[i]][i]=1;for(int i=2;i<=n;i++)//遍历到第i行for(int j=1;j<=cnt;j++)//第i行以第j种状态存在for(int k=K;k>=sta[j];k--)//枚举棋盘上已经摆了k个棋子for(int x=1;x<=cnt;x++)//枚举上一行所有要转移的状态xif(!(sti[j]&sti[x])&&!((sti[j]<<1)&sti[x])&&!((sti[j]>>1)&sti[x]))//判断是否合法f[i][k][j]+=f[i-1][k-sta[j]][x];long long sum=0;for(int j=1;j<=cnt;j++)sum+=f[n][K][j];cout<<sum;return 0;
}两道练习题:
1.#10173. 「一本通 5.4 练习 2」炮兵阵地 - 题目 - LibreOJ (loj.ac)
实现代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,cnt;
int sti[2100],sta[2100];
//滚动数组
int f[2][2100][2100];
//预处理行
char s[100];
void dfs(int x,int num,int cur){if(cur>=m){sti[++cnt]=x;sta[cnt]=num;return;}dfs(x|(1<<cur),num+1,cur+3);dfs(x,num,cur+1);
}
int board[110];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){scanf("%s",s);for(int j=0;j<m;j++) if(s[j]=='H') board[i]|=(1<<j);}dfs(0,0,0);for(int i=1;i<=cnt;i++) if(!(sti[i]&board[2])) for(int j=1;j<=cnt;j++) if(!(sti[j]&board[1])&&!(sti[i]&sti[j])) f[0][i][j]=sta[i]+sta[j];for(int i=3;i<=n;i++)for(int j=1;j<=cnt;j++)for(int x=1;x<=cnt;x++){f[i%2][j][x]=0;if(!(sti[j]&board[i])&&!(sti[x]&board[i-1])&&!(sti[j]&sti[x]))for(int k=1;k<=cnt;k++)if(!(sti[k]&board[i-2])&&!(sti[j]&sti[k])&&!(sti[x]&sti[k]))f[i%2][j][x]=max(f[i%2][j][x],f[(i%2)^1][x][k]+sta[j]);}int ans = 0;if(n==1){for(int i=1;i<=cnt;i++)if(!(board[1]&sti[i]))ans=max(ans,sta[i]);cout<<ans;return 0;}for(int i=1;i<=cnt;i++)for(int j=1;j<=cnt;j++)ans=max(ans,f[n%2][i][j]);cout<<ans;return 0;
}2.P1879 [USACO06NOV] Corn Fields G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
实现代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
const int N = 5E3 + 10;
int cnt;
int board[13];
int sti[N];
long long f[13][N]; // f[i][j]:到了第i行,第i行为第j种状态的草坪
int mod = 1E8;
// 转移方程:
// f[i][j]=sigma f[i-1][x]
void dfs(int x, int cur)
{if (cur >= n){sti[++cnt] = x;return;}dfs(x | (1 << cur), cur + 2);dfs(x, cur + 1);
}
int main()
{cin >> m >> n;for (int i = 1; i <= m; i++){for (int j = 0, k; j < n; j++){scanf("%d", &k);board[i] |= ((k ^ 1) << j);}}dfs(0, 0);for (int i = 1; i <= cnt; i++)if (!(sti[i] & board[1]))f[1][i] = 1;for (int i = 2; i <= m; i++)for (int j = 1; j <= cnt; j++)for (int x = 1; x <= cnt; x++)if (!(sti[j] & sti[x]) && !(sti[j] & board[i]))f[i][j] = (f[i][j] + f[i - 1][x]) % mod;long long ans = 0;for (int i = 1; i <= cnt; i++)ans = (ans + f[m][i]) % mod;cout << ans;return 0;
}二、
集合问题:
上文提到,用二进制对应位置的1,可表示该编号的元素存在于集合中,那么每一个二进制数就可以代表一个状态压缩的集合
我们先来熟悉以下几种位运算操作:
1.对于一个数x而言,x-1的二进制表达与x的区别在于,x-1将x的最低位的1变为了0,且这个1往后的更低位的0全都变为了1
那么如果我们进行x&(x-1)的操作,以x最低位的1为分界点,其往低位(包括其自身)都将变为0,而其更高位的x所对应的1保持不变,也就是说,如果我们进行x&(x-1)而得到的新的二进制数,实际上是把x的最低位的1变为0,其他保持不变所得到的新的二进制数
2.对于一个数而言,如果他是2的非负整数幂,它的二进制表达中一定只有一个1,且会在某个位置
由上述的x&(x-1)的操作我们可知,如果x是2的非负整数幂,那么一定有x&(x-1)==0
3.对于一个数x所代表的集合而言, 我们可通过消除其二进制表达的若干个1,从而得到他的全部子集,实现代码如下:
for(int s=m;s;s=(s-1)&m){
}每进行一次迭代,都会得到一个s,s为m的一个非空子集的状态压缩
4.遍历元素个数为n的集合的子集的子集:
实现代码如下:
for(int m=0;m<(1<<n);m++){//第一个for遍历元素为n的集合的子集for(int s=m;s;s=(s-1)&m){//第二个for遍历子集的子集}
}该操作的时间复杂度为,证明略
5.求集合a对全集u的补集b
则b=a^u
6.求集合a对全集u的交集b
则b=a&u
7.求集合a对全集u的并集b
则b=a|u
例题:
P5911 [POI2004] PRZ - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
实现代码:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int W,n;
int t[20],w[20],tim[70000];
const int INF=(1<<30);
//总共16个人
//记录所有合法子集的状态
//那么dp[i]表示状态为i的情况下,所用时的最短时间
//最后一定是求状态为全满的的dp值
//那么转移方程为:
//dp[i]=min(dp[a]+dp[b]),其中a|b==i
//也就是说a是i的全部子集
//那么b就是a对于i的补集
void check(int tmp,int total,int cost){for (int i = 0; i < n; i++){if ((tmp >> i) & 1){cost = min(cost, t[i]);total += w[i];}if(total>W) return;}tim[tmp]=cost;
}
int main(){cin>>W>>n;for(int i=0;i<n;i++) cin>>t[i]>>w[i];int N=(1<<n)-1;for(int m=N;m;m=(m-1)&N){tim[m]=INF;check(m,0,INF);}for(int m=0;m<(1<<n);m++)for(int s=m;s;s=(s-1)&m)tim[m]=min(tim[m],tim[s]+tim[m^s]);cout<<tim[N];return 0;
}相关文章:
状态压缩动态规划——状压dp
状压dp:意思是将状态进行压缩,从而更容易地写出状态转移方程 通常做法:将每个状态(一个集合)用二进制表示,每个位的1就代表着这个编号的元素存在,0就代表着这个编号的元素不存在,如…...

【算法】最短路径算法思路小结
一、基础:二叉树的遍历->图的遍历 提到搜索算法,就不得不说两个最基础的思想: BFS(Breadth First Search)广度优先搜索 DFS(Depth First Search)深度优先搜索 刚开始是在二叉树遍历中接触这…...

zabbix7.0TLS-05-快速入门-触发器
文章目录 1 概述2 查看主机的触发器3 添加触发器3.1 触发器配置项介绍3.2 扩展文档3.2.1 关于配置项中每个键值返回值的说明3.2.2 触发器函数文档 4 验证触发器5 问题5.1 查了问题总列表5.2 查看问题详情5.3 更新处理问题5.4 查看已经处理的问题 6 问题恢复 1 概述 监控项用于…...

vue关于双向数据绑定的骚操作
组件传值大家都知道 直接上代码 computed: {optionModel: {get() {return this.selectedWidget.options;},set(newValue) {this.selectedWidget.options newValue;}}} 我们将optionModel传递给子组件 子组件可以直接修改props 来实现双向数据绑定 但是正常来时我们是不能修…...

基于Jeecgboot3.6.3的vue3版本的流程中仿钉钉流程的鼠标拖动功能支持
因为这个项目license问题无法开源,更多技术支持与服务请加入我的知识星球。 1、因为原先仿钉钉流程里不能进行鼠标拖动来查看流程,所以根据作者提供的信息进行修改,在hooks下增加下面文件useDraggableScroll.ts import { ref, onMounted, on…...
Docker Compse单机编排
一.Docker Compse 介绍 Docker Compose 是一个用于定义和运行多容器 Docker 应用程序的工具。通过 Compose,你可以使用 YAML 文件来配置应用程序的服务、网络和卷,然后使用单个命令创建和启动所有服务。这使得在开发、测试和部署过程中管理多容器应用程…...

“AI+Security”系列第2期(一):对抗!大模型自身安全的攻防博弈
近日,由安全极客、Wisemodel 社区和 InForSec 网络安全研究国际学术论坛联合主办的“AISecurity”系列第 2 期——对抗!大模型自身安全的攻防博弈线上活动如期举行。本次活动邀请了君同未来创始人兼 CEO 韩蒙、前阿里云高级安全专家郑瀚、ChaMd5 AI 组负…...

Python Static Typing: 提升代码可靠性与可读性的使用技巧
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storm…...

Datawhale多模态赛事(1)
赛事说明:https://tianchi.aliyun.com/competition/entrance/532251/introduction?spma2c22.12281925.0.0.2f307137p8qZmp 学习平台:https://linklearner.com/home 第一天 1.报名赛道学习赛事 https://tianchi.aliyun.com/competition/entrance/53225…...

云手机在海外社交媒体运营中的作用
随着社交媒体的全球普及,海外社交媒体运营成为众多企业与个人提升品牌影响力和扩大市场份额的重要策略。在这一进程中,海外云手机以其独特的功能,为海外社交媒体运营提供了强大的支持。 那么,海外云手机在海外社交媒体运营中究竟扮…...

Ubuntu怎么进入救援模式或单用户模式
进入救援模式(Rescue Mode)或单用户模式(Single User Mode)的方法取决于你所使用的Linux发行版。以下是通用的步骤,适用于大多数基于GRUB引导的系统,如Ubuntu、Debian、CentOS等: 重启你的系统。…...

学习鸿蒙-构建私有仓储
1.选择 鸿蒙提供ohpm-repo工具用于构建本地私有仓储 ohpm-repo下载 2.环境配置 安装node,ohpm-repo 支持 node.js 18.x 及以上版本 node最新版本下载 3.配置文件及运行 1.解压 ohpm-repo 私仓工具包 2.进入 ohpm-repo 解压目录的 conf 目录内,打开 c…...

经验是负债,学习是资产
经验是负债,学习是资产 经验是负债,学习是资产。这是李嘉诚先生的一句名言。他一语道出了学习在企业发展中的推动作用。 企业家经营的目的,无非就是将利润最大化。企业能够产生利润,靠的是提升自身业绩、降低运营成本,…...
电脑屏幕录制工具分享5款,附上详细电脑录屏教程(2024全新)
日月更迭,转眼间已经来到了2024年的立秋,在这个数字技术快速发展的时代,电脑录屏技术已经成为了一项不可或缺的技能,无论是用于工作汇报、在线教学、游戏直播还是个人娱乐。那么录屏软件哪个好用呢?接下来,…...

Docker资源隔离的实现策略以及适用场景
Docker通过多种技术实现资源隔离,确保不同容器之间相互独立并有效利用主机资源。 以下是Docker资源隔离的主要实现策略以及适用场景: 实现策略 1、命名空间(Namespaces) 进程命名空间(PID Namespace): 隔…...
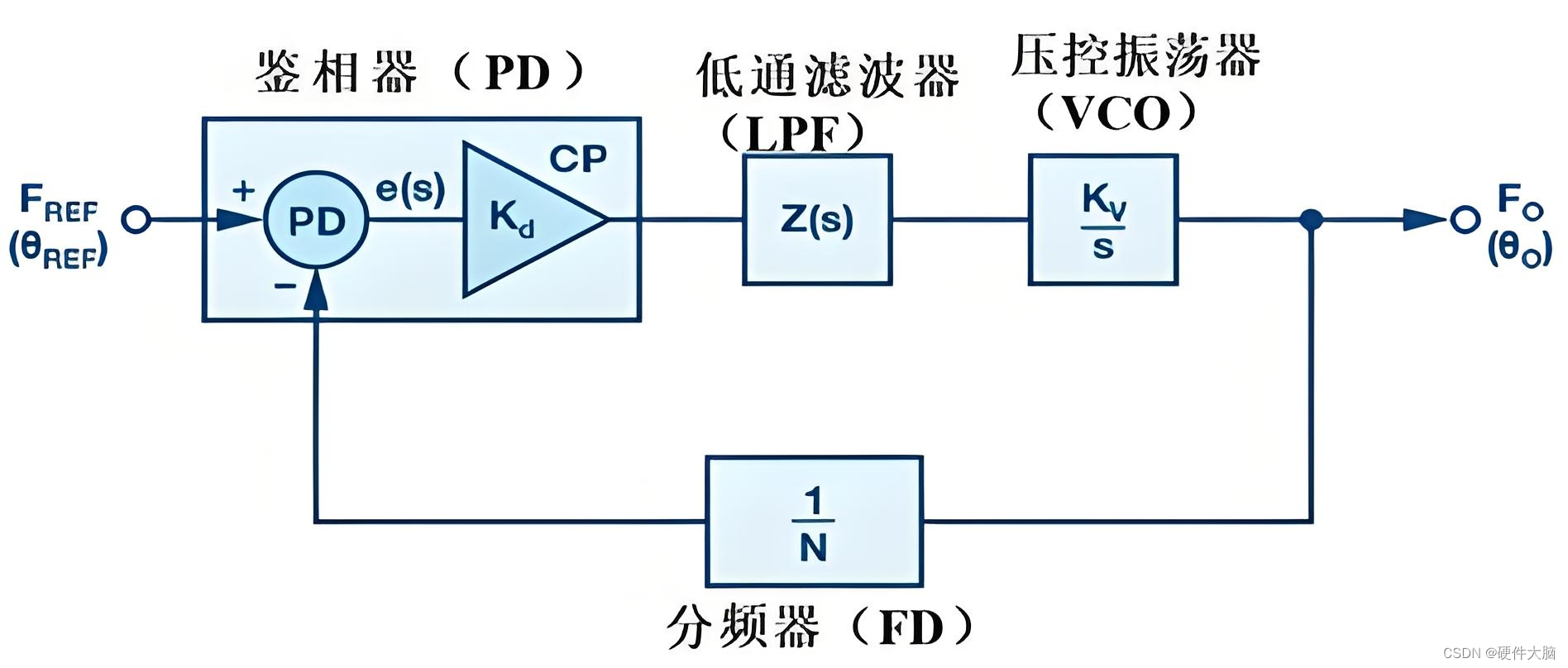
PLL基本原理、设计及应用
PLL基本原理 锁相环(Phase-Locked Loop, PLL)是一种基本的反馈控制系统,广泛应用于电子通信、信号处理、时钟同步等多个领域。PLL通过反馈机制锁定输入信号的频率和相位,从而实现输出信号与输入信号的同步。其基本工作原理可以概…...

Qt实现类似淘宝商品看板的界面,带有循环翻页以及点击某页跳转的功能
效果如下: #ifndef ModelDashboardGroup_h__ #define ModelDashboardGroup_h__#include <QGridLayout> #include <QLabel> #include <QPushButton> #include <QWidget>#include <QLabel> #include <QWidget> #include <QMou…...

2024下半年国际学术会议一览表
在科技与人文的交汇点,2024年的国际学术会议季即将拉开帷幕,一系列聚焦于计算机科学与人工智能、工程与技术、教育与社会科学的盛会,不仅展示了全球学术研究的最新成果,更促进了跨学科交流与合作,为未来的科技发展与社…...

serial靶场
项目地址 https://download.vulnhub.com/serial/serial.zip 实验过程 将下载好的靶机导入到VMware中,设置网络模式为NAT模式,然后开启靶机虚拟机 使用C段扫描,获取靶机IP地址 arp-scan -l 扫描一下端口 nmap -sV -p- 192.168.48.149 查看…...

如何在Vue3项目中引入并使用Echarts图表
在Vue 3项目中引入并使用ECharts图表,你可以通过npm或yarn来安装ECharts,然后在Vue组件中引入并使用它。以下是一个基本的步骤指南: 1. 安装ECharts 首先,你需要在你的Vue 3项目中安装ECharts。打开你的终端或命令提示符&#x…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
