2024牛客暑期多校训练营8
文章目录
- A. Haitang and Game
- E.Haitang and Math
- J. Haitang and Triangle
- K. Haitang and Ava
A. Haitang and Game
通过审题可以知道,最后的胜者和若干次操作后最多能增加的数的奇偶有关。
由于 a i a_i ai 较小,所以我们枚举每一个没出现过的 x , x ∈ [ 1 , 1 e 5 ] x,x\in[1,1e5] x,x∈[1,1e5], 考虑如何让 x x x 出现,很简单,有两个数的 g c d gcd gcd 等于 x x x 呗,好像说了废话。
那我们怎么快速寻找这么两个数呢,在遍历 x x x 的时候查找它的所有倍数,如果出现过并且这些所有的倍数 g c d gcd gcd 值为 x x x 的话则 x x x 可以出现。如果 x % 2 = 1 x\%2=1 x%2=1 先手获胜,否则后手获胜,时间复杂度 O ( T n l o g n ) O(Tnlogn) O(Tnlogn) 。
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define YES "YES"
#define NO "NO"
#define all(a) a.begin(), a.end()
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const double eps = 1e-9;
const int N = 1e6 + 10;
const int M = 1e6 + 10;
const int INF = 1e18 + 10;
const int mod = 1e9 + 7;
const int base = 23333;
const double pi = acos(-1.0);
//mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count());
int a[N];
void solve()
{vector<int> jl(1e5 + 10, 0);int n;cin >> n;for(int i = 1;i <= n;i++){cin >> a[i];jl[a[i]] = 1;}int cnt = 0;for(int i = 1;i <= 1e5;i++){if(jl[i]) continue;int flag = 0, now = 0;for(int j = i;j <= 1e5;j += i){if(jl[j]){if(flag == 0){now = j;flag = 1;}else now = __gcd(now, j);}}if(now == i) cnt++;}if(cnt % 2 == 1) cout << "dXqwq" << '\n';else cout << "Haitang" << '\n';
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;cin >> t;while (t--) solve();return 0;
}
E.Haitang and Math
赛时一直在调 O ( T n ) O(T\sqrt{n}) O(Tn) 的做法,但是没调出来,都这么轻量级了还不让过,真是可恶。
比赛结束之后才发现居然有 P o l l a r d R h o Pollard\ Rho Pollard Rho 这样的黑科技,可以在 n 4 \sqrt[4]{n} 4n 的时间复杂度求得一个数的最大质因子,真是学到了。
求出最大质因子之后就可以通过质因子分解分解出所有的质因子,再通过 d f s dfs dfs 求出所有的因子,对于 [ 1 , 108 ] [1,108] [1,108] 的所有 S ( m ) S(m) S(m) 求一下题目中的式子是否成立即可,注意去重。时间复杂度有点玄学,大概是 O ( T n l o g n ) O(\frac{T\sqrt{n}}{logn}) O(lognTn),交上去之后跑的飞起,这个故事告诉我们,学好算法还是很重要滴。
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define YES "YES"
#define NO "NO"
#define all(a) a.begin(), a.end()
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const double eps = 1e-9;
const int N = 1e6 + 100;
const int M = 1e6 + 10;
const int INF = 1e18 + 100;
const int mod = 1e9 + 7;
const int base = 23333;
// mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count());
int max_factor, n, nn;
int quick_pow(int x, int p, int mod) // 快速幂
{int ans = 1;while (p){if (p & 1) ans = (__int128)ans * x % mod;x = (__int128)x * x % mod;p >>= 1;}return ans;
}
bool Miller_Rabin(int p) // 判断素数
{if (p < 2) return 0;if (p == 2) return 1;if (p == 3) return 1;int d = p - 1, r = 0;while (!(d & 1)) ++r, d >>= 1; // 将d处理为奇数for (int k = 0; k < 10; ++k){int a = rand() % (p - 2) + 2;int x = quick_pow(a, d, p);if (x == 1 || x == p - 1) continue;for (int i = 0; i < r - 1; ++i){x = (__int128)x * x % p;if (x == p - 1) break;}if (x != p - 1) return 0;}return 1;
}
int Pollard_Rho(int x)
{int s = 0, t = 0;int c = (int)rand() % (x - 1) + 1;int step = 0, goal = 1;int val = 1;for (goal = 1;; goal *= 2, s = t, val = 1) // 倍增优化{for (step = 1; step <= goal; ++step){t = ((__int128)t * t + c) % x;val = (__int128)val * abs(t - s) % x;if ((step % 127) == 0){int d = __gcd(val, x);if (d > 1) return d;}}int d = __gcd(val, x);if (d > 1) return d;}
}
void fac(int x)
{if (x <= max_factor || x < 2) return;if (Miller_Rabin(x)) // 如果x为质数{max_factor = max(max_factor, x); // 更新答案return;}int p = x;while (p >= x) p = Pollard_Rho(x); // 使用该算法while ((x % p) == 0) x /= p;fac(x), fac(p); // 继续向下分解x和p
}
vector<int> pri;
map<int, int> mp, cnt;
int ans;
int coun(int x)
{int res = 0;while(x > 0){res += x % 10;x /= 10;}return res;
}
void dfs(int now, int res, int tt)
{//cout << now << " " << res << " " << tt << '\n';if(res > tt) return;if(now == pri.size()){if(tt % res == 0 && n % res != 0 && !cnt[res] && coun(res) == n - tt){//cout << res << '\n';cnt[res] = 1;ans++;}return;}dfs(now + 1, res, tt);if(mp[pri[now]]){mp[pri[now]]--;dfs(now, res * pri[now], tt);mp[pri[now]]++;}
}
void solve()
{srand((unsigned)time(NULL));cin >> n;ans = 0;cnt.clear();for(int ii = 1;ii <= min(n - 2, 108LL);ii++){pri.clear();mp.clear();max_factor = 0;nn = n - ii;fac(nn);pri.push_back(max_factor);nn /= max_factor;mp[max_factor]++;for(int i = 2; i <= nn / i; ++i) {if(nn % i == 0){pri.push_back(i);while (nn % i == 0) {mp[i]++;nn /= i;}}}if (nn > 1){mp[nn]++;pri.push_back(nn);}//cout << n - ii << " " << pri.size() << '\n';//for(auto u : pri) cout << u << " " << mp[u] << '\n';dfs(0, 1, n - ii);}cout << ans << '\n';
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;cin >> t;while (t--) solve();return 0;
}
J. Haitang and Triangle
n n n 个数相邻三三组合最多有 n − 2 n-2 n−2 种组合方式,但是包含 1 1 1 的那一组一定组成不了三角形,所以 k = n − 2 k=n-2 k=n−2 时无解。
k = 0 k=0 k=0 时,形如 d , 2 d , 3 d , d − 1 , 2 d − 1 , 3 d − 1 , … , 1 , 1 + d , 1 + 2 d d,2d,3d,d-1,2d-1,3d-1,\dots,1,1+d,1+2d d,2d,3d,d−1,2d−1,3d−1,…,1,1+d,1+2d 这样的排列是满足条件的, d = ⌊ ( n − k ) 3 ⌋ d=\lfloor \frac{(n-k)}3 \rfloor d=⌊3(n−k)⌋。
那 k > 0 k>0 k>0 怎么放呢,不难发现,把除了 1 1 1 的其他 m m m 个数按顺序发如 2 , 3 , 4 , … , m 2,3,4,\dots,m 2,3,4,…,m,每个长度为三的字串都能构成一个三角形,所以我们左边放 k = 0 k=0 k=0 时的情况,右边放其他数。再根据 d % 3 d\%3 d%3 的不同值往端点插入数,增加构不成三角形的区间长度,时间复杂度 O ( ∑ n ) O(\sum{n}) O(∑n)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define YES "YES"
#define NO "NO"
#define all(a) a.begin(), a.end()
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const double eps = 1e-9;
const int N = 1e6 + 100;
const int M = 1e6 + 10;
const int INF = 1e18 + 100;
const int mod = 1e9 + 7;
const int base = 23333;
// mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count())
void solve()
{int n, m;cin >> n >> m;vector<int> flag(n + 5);if(m == n - 2){cout << -1 << '\n';return;}int x = n - m;int d = x / 3;vector<int> ans;if (x % 3 == 0) {for (int i = 0;i < d;i++) {ans.push_back(d - i);ans.push_back(2 * d - i);ans.push_back(3 * d - i);}for (int i = 1;i <= m;i++) ans.push_back(3 * d + i);}if (x % 3 == 1) { ans.push_back(n);for (int i = 0;i < d;i++) {ans.push_back(d - i);ans.push_back(2 * d - i);ans.push_back(3 * d - i);}for (int i = 1;i <= m;i++) ans.push_back(3 * d + i);}if (x % 3 == 2) {ans.push_back(3 * d + 1);for (int i = 0;i < d;i++) {ans.push_back(d - i);ans.push_back(2 * d - i);ans.push_back(3 * d - i);}ans.push_back(3 * d + 2);for (int i = 3;i <= m + 2;i++) ans.push_back(3 * d + i);}for (auto x : ans) cout << x << " ";cout << "\n";
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;cin >> t;while (t--) solve();return 0;
}
K. Haitang and Ava
从前往后匹配 a v a ava ava 或者 a v a v a avava avava 串,如果能匹配完输出 Y e s Yes Yes ,否则输出 N o No No ,时间复杂度 O ( ∑ S ) O(\sum{S}) O(∑S)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define YES "YES"
#define NO "NO"
#define all(a) a.begin(), a.end()
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const double eps = 1e-9;
const int N = 1e6 + 10;
const int M = 1e6 + 10;
const int INF = 1e18 + 10;
const int mod = 1e9 + 7;
const int base = 23333;
const double pi = acos(-1.0);
//mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count());
void solve()
{string s;cin >> s;int pos = 0;for(int i = 0;i < s.size();){if(i + 5 <= s.size()){if(s[i] == 'a' && s[i + 1] == 'v' && s[i + 2] == 'a' && s[i + 3] == 'v' && s[i + 4] == 'a'){i += 5;pos = i;}else if(s[i] == 'a' && s[i + 1] == 'v' && s[i + 2] == 'a'){i += 3;pos = i;}else break;}else if(i + 3 <= s.size()){if(s[i] == 'a' && s[i + 1] == 'v' && s[i + 2] == 'a'){i += 3;pos = i;}else break;}else break;}if(pos == s.size()) cout << "Yes" << '\n';else cout << "No" << '\n';
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;cin >> t;while (t--) solve();return 0;
}
相关文章:

2024牛客暑期多校训练营8
文章目录 A. Haitang and GameE.Haitang and MathJ. Haitang and TriangleK. Haitang and Ava A. Haitang and Game 通过审题可以知道,最后的胜者和若干次操作后最多能增加的数的奇偶有关。 由于 a i a_i ai 较小,所以我们枚举每一个没出现过的 x …...

git的一些操作指令
一、git 提交规范 commit message subject : 空格 message 主体 feat: 新功能(feature)用于提交新功能。fix: 修复 bug用于提交 bug 修复。docs: 文档变更用于提交仅文档相关的修改。style: 代码风格变动(不影响代码逻辑&…...

【IT行业研究报告】Internet Technology
一、引言 随着信息技术的飞速发展,IT行业已成为全球经济的重要驱动力。从云计算、大数据、人工智能到物联网,IT技术正深刻改变着各行各业的生产方式、商业模式和人们的生活方式。本报告旨在深入分析IT行业的现状、发展趋势和挑战,探讨其在各…...
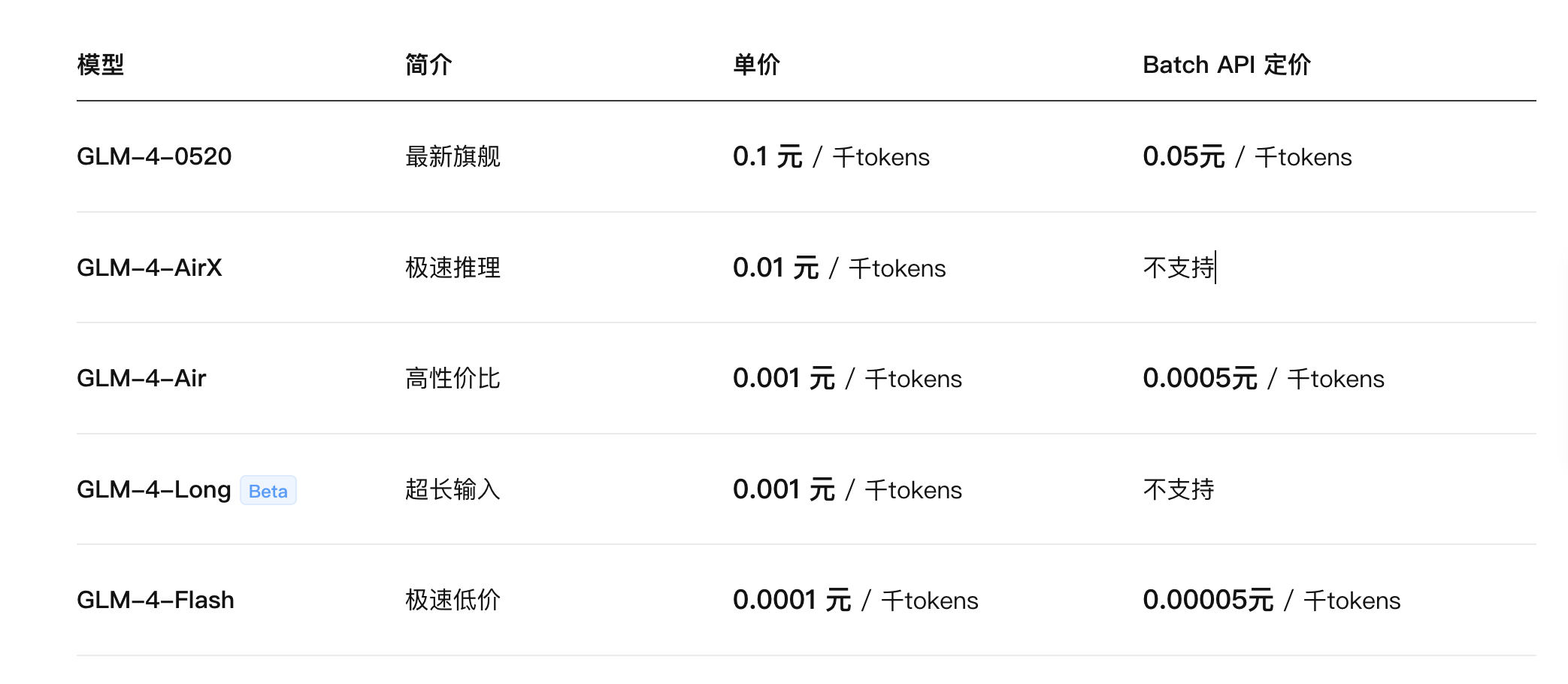
GLM大模型的机器翻译能力测试
背景介绍 最近想对GLM-4今年发布的几个大模型 glm-4-0520,glm-4-air以及glm-4-flash简单评测一下它们的机器翻译能力,由于这几个大模型的容量和训练数据都有区别,所以它们的翻译能力也是不同的。我们这里就分别选择一些有趣的,有…...

【硬件产品经理】汽车A样设计
目录 简介 制造方式 作者简介 简介 一般被称作原型样件(Prototype)。 主要是根据系统需求设计,实现基本功能和关键尺寸,用于基本功能的验证,用于初期产品软件调试和Hil台架测试(Hardware in Loop,硬件在环)的样机阶段。 也就说在设计初期,A样的主要目的可以划分…...

Ubuntu22.04系统中安装机器人操作系统ROS
在Ubuntu 22.04上安装ROS(Robot Operating System)的过程可以分为几个主要步骤。请注意,ROS有不同的版本(如ROS 1的Melodic、Noetic等,以及ROS 2的Foxy、Humble等),这些版本对Ubuntu的支持程度可…...

LeetCode54题:螺旋矩阵(原创)
【题目描述】 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:mat…...

FPGA常见型号
FPGA(现场可编程门阵列)开发板种类繁多,涵盖了从入门级教育用途到高性能工业应用的广泛领域。以下是一些常见的 FPGA 开发板型号及其特点: 1. Xilinx(赛灵思)系列 Xilinx 是 FPGA 领域的领导者之一&#…...

【多模态大模型】FlashAttention in NeurIPS 2022
一、引言 论文: FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness 作者: Stanford University 代码: FlashAttention 特点: 该方法提出将Q、K、V拆分为若干小块,使执行注意力时不需要频…...

过滤器doFilter 方法
在Java EE中,过滤器的放行是指在过滤器的 doFilter 方法中调用 FilterChain 对象的 doFilter 方法,将请求传递给下一个过滤器或目标 servlet 进行处理。这个过程可以理解为过滤器的责任链传递。 过滤器的 doFilter 方法 在过滤器中,实现 Fil…...

WPF篇(9)-CheckBox复选框+RadioButton单选框+RepeatButton重复按钮
CheckBox复选框 CheckBox继承于ToggleButton,而ToggleButton继承于ButtonBase基类。 案例 前端代码 <StackPanel Orientation"Horizontal" HorizontalAlignment"Center" VerticalAlignment"Center"><TextBlock Text"…...

【机器学习基础】线性回归
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

java基础概念12-二维数组
一、二维数组的定义 二维数组可以被视为数组的数组,即每个元素都是一个数组。 二维数组的应用场景: 当我们需要把数据分组管理的时候,就需要用到二维数组。 二、二维数组的初始化 2-1、静态初始化 阿里巴巴规范手册: // 静态初始…...

56 锐键交换机开局
锐键交换机开局 一 锐键视图切换 1 Ruijie> 用户视图 2 Ruijie# 特权模式 3 Ruijie(config)# 全局配置模式 4 Ruijie(config-if-GigabitEthernet 1/1/1)# 接口配置模式 5 Ruijie(config)#show vlan 6 exit (退出) 7 enable(进入)...

VR虚拟展厅与传统实体展厅相比,有哪些优势?
视创云展虚拟展厅相比传统的实体展厅具有多方面的优势,主要体现在以下几个方面: 1、降低成本: 虚拟展厅无需租赁或建设物理空间,减少了场地、装修和维护等方面的开支。同时,参观者和参展商无需现场参观或布展&#x…...

Vue的事件处理、事件修饰符、键盘事件
目录 1. 事件处理基本使用2. 事件修饰符3. 键盘事件 1. 事件处理基本使用 使用v-on:xxx或xxx绑定事件,其中xxx是事件名,比如clickmethods中配置的函数,都是被Vue所管理的函数,this的指向是vm或组件实例对象 <!DOCTYPE html&g…...
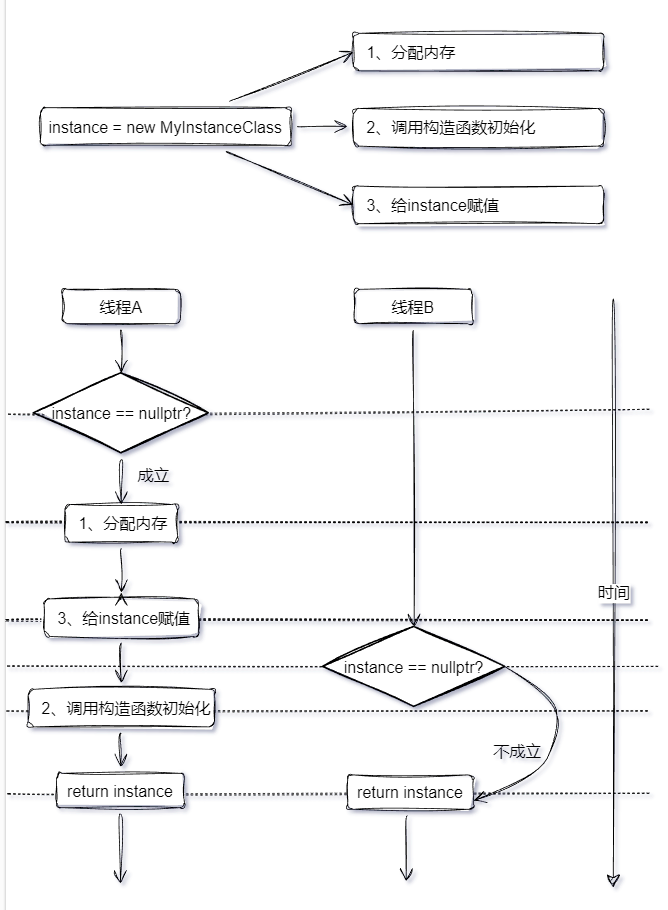
c++单例实践
C单例实践 在日常开发中,虽然太多的单例调用会让代码的耦合度变高,但是例如日志类这种,单例模式就变得非常有。所以这篇文章为大家介绍static 关键字相关知识以及如何实现自己的C单例类。 static关键字 首先让我们请出今天的主角: static。…...

SQL注入实例(sqli-labs/less-9)
0、初始页面 1、爆库名 使用python脚本 def inject_database1(url):name for i in range(1, 20):low 32high 128mid (low high) // 2while low < high:payload "1 and if(ascii(substr(database(),%d,1)) > %d ,sleep(2),0)-- " % (i, mid)res {"…...

http不同类型方法的作用,get和post区别
在HTTP协议中,不同的请求方法用于不同的操作。常见的HTTP方法包括GET、POST、PUT、DELETE、HEAD、OPTIONS、PATCH等,每种方法有其特定的作用。 常见的HTTP方法及其作用 1. GET - **作用**: 从服务器请求指定资源。GET方法通常用于获取数据而不会修改数据…...

# 利刃出鞘_Tomcat 核心原理解析(二)
利刃出鞘_Tomcat 核心原理解析(二) 一、 Tomcat专题 - Tomcat架构 - HTTP工作流程 1、Http 工作原理 HTTP 协议:是浏览器与服务器之间的数据传送协议。作为应用层协议,HTTP 是基于 TCP/IP 协议来传递数据的(HTML文件…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
