红黑树的插入与删除
文章目录
- 红黑树概念
- 红黑树的`性质`:
- 红黑树的插入操作
- 情况一
- 情况二
- 情况三
- 小总结
- 红黑树的验证
- 红黑树的删除
- 一.删除单孩子节点
- 1. 删除节点颜色为黑色
- 2. 删除颜色为红色
- 二. 删除叶子节点
- 1. 删除节点为红色
- 2.删除节点为黑色
- 2.1兄弟节点为黑色,有孩子节点,并且孩子节点再兄弟节点的同一侧
- 2.2. 兄弟节点为黑色,有孩子节点,并且孩子节点再兄弟节点的另一侧
- 2.3 兄弟节点为黑色,无孩子节点或者孩子节点都为黑色。
- 2.4 兄弟节点为红色
- 代码实现:
红黑树概念
先来回顾一下AVL树:在我们讲解AVL树的时候,我们会设置一个平衡因子来控制我们树的高度,通过右子树-左子树这种方式来表示我们平衡因子的大小,如果bf的绝对值大于·1,那就说明不平衡,此时需要旋转处理从而让树达到平衡。(绝对平衡)
而红黑树是设置一个颜色并通过一些性质来是红黑树达到近似平衡。(每个节点不是红色的就是黑色的)
红黑树的性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的 (重点)(不能有连续的红色节点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(重点)(每条路径黑色节点数量相同)
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
这里对第三点做个解释:不能存在连续的红色节点。同时有了上面的性质限制,我们就可以保证二叉树最长路径不超过最短路径的两倍。(为什么呢?)

红黑树中我们可以吧每一个空节点代表为一条路径,所以上图我们一共就有11条路径,那么每一条路径中我们黑色节点的数量都为两个(虽然空节点代表黑色,这里不加入计算)那么最短路径就是全为黑色节点的路径,最长路径就是一黑一红交错的路径。所以由于我们第四条性质限定了我们每条路径的黑色节点数量必须相同,所以才会有最长路径不超过最短路径的两倍这样一个结论。
- 为了方便以后实现map和set的封装,代买实现都是添加了一个头节点。
红黑树的插入操作
在了解插入操作的时候,我们要明确新增的节点一定为红色。
由于根节点一定为黑色,又要保证第四条性质的黑数同,所以当我们新增的节点一定为黑色。

同时为了方便描述,我们把新增节点命名为:c(cur),新增节点的父节点为p(parent),父节点的兄弟节点命名为:u(uncle),g(grandfather):爷爷节点
情况一
当我们了解了上面的知识过后,我们来分析一下:我们左边插入和右边插入都没有问题。

看下面的情况:

如果我们这样插入呢?由于性质三规定了不能存在连续的红色节点,所以此时我们需要调整,那如何调整呢?
情况一:c为新增,u为红,p为红,g为黑(也只能是黑色,不可能有连续的红色节点)
解决方案:此时我们只需要让u和p变黑,然后g变红,把g赋值给c,继续向上调整。
我们先来看一个简单的栗子:

上图是我们g节点为根的情况,还有可能为一棵树的子树,所以我们还需要继续向上调整。如图:

情况二
c为新增,u存在且为黑/u不存在,p为红,g为黑

解决方法:旋转完之后,只需要让g变红色,p变为黑色即可。同时我们的情况二是由情况一变过来的。

情况三
c为新增但是p的另一侧,u存在且为黑/u不存在,p为红,g为黑

解决方法:双旋完之后,让g变为红色,c变为黑色。双旋逻辑和AVL树一样,只不过这里我们并不需要维护平衡因子了。
小总结
插入过程种,当我们c为红色,p为红色的时候违反了性质三,所以我们需要进行处理,所以处理的结束条件就是当我们p为黑色的时候就不需要处理了。情况二和情况三旋转完之后已经不需要处理了。
原因:
旋转的时候g有两种情况:1.根 2. 子树
-
作为根的话,旋转完毕就结束了
-
作为子树,它的父节点一定为黑色节点,所以当我们旋转完之后把
c变为g的位置的时候,p的指向为黑色节点,所以也不需要继续调整了。
由于我们新增节点必须为红色,旋转的条件是一黑一红,而且旋转只能由情况一转化为情况二才进行旋转,那么既然有红色节点那么g肯定为黑色,那么g->_parent节点也一定为黑色,如果g->_parent是红色的话,那我们不就相当于新增了一个黑色节点了吗,这样是不行的。所以旋转完之后没有必要继续调整。
代码实现:
bool insert(const K& key){//只有一个头节点if (pHead->_parent == pHead){pHead->_parent = new Node(key);pHead->_parent->_parent = pHead;pHead->_parent->_col = BLACK;return true;}Node* cur = pHead->_parent;Node* parent = cur->_parent;while (cur){if (key < cur->_data){parent = cur;cur = cur->_left;}else if (key > cur->_data){parent = cur;cur = cur->_right;}elsereturn false;}cur = new Node(key);cur->_parent = parent;//连接新增节点与父节点的关系if (parent->_data > key)parent->_left = cur;elseparent->_right = cur;Node* grandfather = parent->_parent;Node* uncle = nullptr;//满足parent的颜色是红色节点 并且 parent不是哨兵节点。while (parent->_col == RED && parent != pHead){if (grandfather->_left == parent)uncle = grandfather->_right;elseuncle = grandfather->_left;if (uncle && uncle->_col == RED) //p红色,u红色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = grandfather->_parent;grandfather = parent->_parent;}else if ((uncle && uncle->_col == BLACK) || uncle == nullptr){//右单旋if (grandfather->_left == parent && parent->_left == cur){RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else if (grandfather->_right == parent && parent->_right == cur){//左单旋RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else if (grandfather->_left == parent && parent->_right == cur){//左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}else if (grandfather->_right == parent && parent->_left == cur){//右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}else{assert(false);}}pHead->_parent->_col = BLACK;return true;}
红黑树的验证
我们只需要根据性质进行验证即可:
- 根节点为黑色
- 不能存在连续的红色节点
- 每条路径中黑色数量相同
那如何求每一条路径的黑色节点数量呢?每次遍历到空节点其实就是一条路径完全走完了。
代码实现:
bool IsRBTree(){return _isRBTree(pHead->_parent);}
int Height(){return TreeHigh(pHead->_parent);}
private:int TreeHigh(Node* root){if (root == nullptr || root->_parent == root)return 0;return max(TreeHigh(root->_left),TreeHigh(root->_right)) + 1;}bool _isRBTree(Node* root){//只有一个头节点if (root->_parent == root)return true;Node* LeftMost = root;if (root->_col != BLACK){cout << " 违反性质二:根节点为黑色 " << endl;return false;}int k = 0;while (LeftMost){if (LeftMost->_col == BLACK)k++;LeftMost = LeftMost->_left;}return IsSameBlack(root->_left,1,k) && IsSameBlack(root->_right, 1, k);}bool IsSameBlack(Node* root, size_t cnt, int k){if (root == nullptr){cout << "当前路径黑色节点数量:" << cnt << endl;if (cnt != k){cout << "违反性质四:每条路径中的黑色节点数量不一样 " << endl;return false;}return true;}if (root->_col == BLACK)cnt++;Node* parent = root->_parent;if (parent != pHead && parent->_col == RED && root->_col == RED){cout << " 违反性质三:不能有连续的红色节点" << endl;return false;}return IsSameBlack(root->_left, cnt, k) && IsSameBlack(root->_right, cnt, k);}
红黑树的删除
红黑树的删除和二叉搜索树的删除类似都有三种情况:
- 删除叶子节点
- 删除单孩子节点
- 删除双孩子节点
我们先来回忆以下双孩子节点如何删除,我们需要去找一个替换节点来替换此时的删除节点,那么这个替换节点需要满足:
- 比要删除的左子树大
- 比要删除的右子树小
所以我们有两种选择:1. 左子树的最大节点 2. 右子树的最小节点。接下来我实现的都是找右子树的最小节点。
那么当我们找到这个可替换节点的时候无非就是两种情况: 1. 可替换节点为叶子节点 2. 可替换节点为单孩子节点。
那么其实我们删除两个孩子节点的操作当我们把可替换节点的值赋值给要删除节点的时候,其实就变为了删除叶子节点或者删除单孩子节点。
有了上面的理解,我们可以值需要梳理删除叶子节点和删除单孩子节点的思路即可。
这里我们先来说删除单孩子节点。
一.删除单孩子节点
这里分为两种情况:
- 删除节点颜色为黑色
- 删除节点为红色
1. 删除节点颜色为黑色
此时我们那个孩子节点的颜色只有一种情况,那就是红色节点,那么由于我们删除过后会少一个黑色节点,所以当我们连接新的节点过后,要把这个红色节点变为黑色。

2. 删除颜色为红色
那它的孩子节点一定为黑色,直接连接孩子节点与父节点的关系,然后直接删除即可。
二. 删除叶子节点
1. 删除节点为红色
直接删除即可,然后需要把父节点对应的左右孩子置空,不然后面会访问野指针(O.0!)
2.删除节点为黑色

如上图,如果我们把节点6删除过后,那最左边的路径黑色节点就会少一个,这样就违反了第四条性质。这时候我们就要分类讨论它的兄弟节点的颜色了。
2.1兄弟节点为黑色,有孩子节点,并且孩子节点再兄弟节点的同一侧
这里我们都以s称为兄弟节点,sr就是兄弟节点的右子树。

如上图,进行单选的时候我们需要把颜色依次赋值:sr->_col = s->_col,s->_col = p->_col,p->_col = BLACK。
同理进行右单旋也是如此,这里就不再赘述了。
2.2. 兄弟节点为黑色,有孩子节点,并且孩子节点再兄弟节点的另一侧
这个时候就是双旋了。

双旋唯一不一样的就是颜色的变换,这个时候我们直接让 sl->_col = p->_col,p->_col = BLACK,这时候直接让兄弟节点的孩子节点复制父亲节点的颜色,然后父亲节点变黑,最后进行双旋操作即可。
2.3 兄弟节点为黑色,无孩子节点或者孩子节点都为黑色。
这个时候需要先把兄弟节点变红,然后再观察现在的parent(父亲节点):
- 如果父亲节点为红色或者为根,直接让父亲节点变为黑色,最后删除节点即可。
- 如果父亲节点为黑色并且不是根节点的话,就要继续观察,然后重复我们删除节点为黑色的这个操作

2.4 兄弟节点为红色
此时直接交换兄弟节点与父亲节点的颜色,然后对p(父亲节点)进行向着删除节点的方向进行旋转,如果删除节点再p左侧就进行左旋,如果删除节点再p右侧就进行右旋。然后继续观察当前的删除节点,继续重复删除节点为黑色的操作

代码实现:
//进来的都是叶子节点为黑色的情况,那么如果叶子节点为黑色的话,一定有兄弟节点。不然违反了性质4.
void ChangeColor(Node* cur, Node* parent)
{Node* uncle = nullptr;//1. 如果uncle是黑色节点,并且它有红色的孩子节点(旋转的状态)//2. 如果uncle是黑色节点,并且他的孩子都是黑色节点(NULL也算),那么就把兄弟节点变为红色同时向上遍历双重黑色节点//3. 如果uncle是红色节点,交换兄弟和parent的颜色,然后向删除节点的方向旋转,然后继续观察兄弟节点while (parent != pHead){if (parent->_left == cur){uncle = parent->_right;}else{uncle = parent->_left;}if (uncle->_col == BLACK){//进行右单旋if (parent->_left == uncle && uncle->_left && uncle->_left->_col == RED){Node* uncle_left = uncle->_left;//变色uncle_left->_col = uncle->_col;uncle->_col = parent->_col;parent->_col = BLACK;//旋转RotateR(parent);break;}else if (parent->_right == uncle && uncle->_right && uncle->_right->_col == RED){//进行左单旋Node* uncle_right = uncle->_right;//变色uncle_right->_col = uncle->_col;uncle->_col = parent->_col;parent->_col = BLACK;RotateL(parent);break;}else if (parent->_left == uncle && uncle->_right && uncle->_right->_col == RED){//进行左右双旋Node* uncle_right = uncle->_right;//变色uncle_right->_col = parent->_col;parent->_col = BLACK;RotateL(uncle);RotateR(parent);break;}else if (parent->_right == uncle && uncle->_left && uncle->_left->_col == RED){//进行右左双旋Node* uncle_left = uncle->_left;//变色uncle_left->_col = parent->_col;parent->_col = BLACK;RotateR(uncle);RotateL(parent);break;}else if ((uncle->_left == nullptr && uncle->_right == nullptr) || (uncle->_left && uncle->_right && uncle->_left->_col == BLACK && uncle->_right->_col == BLACK)){//兄弟节点的孩子全为黑色节点//把兄弟节点变为红色,然后双重黑色节点往上调继续遍历uncle->_col = RED;//遍历到根节点或者红色节点把节点变为黑色退出即可。if ((uncle->_parent != pHead->_parent && uncle->_parent->_col == RED) || (uncle->_parent == pHead->_parent)){uncle->_parent->_col = BLACK;break;}else{cur = uncle->_parent;parent = cur->_parent;}}}else if (uncle->_col == RED){//交换uncle和parent的颜色,Parent变为黑色,然后向删除节点方向旋转,再看双重黑节点uncle->_col = parent->_col;parent->_col = RED;if (parent->_left == cur){RotateL(parent);}else{RotateR(parent);}cur = cur;parent = cur->_parent;}}}bool erase(const K& key)
{//只有一个哨兵节点无法删除。if (pHead->_parent == pHead)return false;Node* cur = pHead->_parent;Node* parent = pHead;while (cur){if (key < cur->_data){parent = cur;cur = cur->_left;}else if (key > cur->_data){parent = cur;cur = cur->_right;}else{//叶子节点if (cur->_left == nullptr && cur->_right == nullptr){//如果删除的是根节点,直接让哨兵的parent指针指向自己。if (parent == pHead){pHead->_parent = pHead;delete cur;return true;}else if (cur->_col == RED)//红色的话直接删除{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}else if (cur->_col == BLACK) //如果删除的节点为黑色节点{ChangeColor(cur,parent);if (parent->_left == cur)parent->_left = nullptr;elseparent->_right = nullptr;delete cur;return true;}}else if (cur->_left == nullptr) //左边为空{//删除的为根节点,直接改变pHead的指向即可。if (parent == pHead){pHead->_parent = cur->_right;if (cur->_right){cur->_right->_col = BLACK;cur->_right->_parent = pHead;}delete cur;return true;}else if (cur->_col == BLACK){//判断为父亲节点的哪一边if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}//如果删除的单孩子节点为黑色,就需要把删除节点的右孩子变为黑色。如果有右孩子的话)if (cur->_right){cur->_right->_col = BLACK;cur->_right->_parent = parent; //如果有的话别忘了连接父节点}delete cur;return true;}else if (cur->_col == RED){//判断为父亲节点的哪一边if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}//如果删除的单孩子节点为红色,直接删除delete cur;return true;}}else if (cur->_right == nullptr){//删除的为根节点,直接改变pHead的指向即可。if (parent == pHead){pHead->_parent = cur->_left;if (cur->_left){cur->_left->_col = BLACK;cur->_left->_parent = pHead;}delete cur;cur = nullptr;return true;}else if (cur->_col == BLACK){//判断为父亲节点的哪一边if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}//如果删除的单孩子节点为黑色,就需要把删除节点的左孩子变为黑色(如果有左孩子的话)if (cur->_left){cur->_left->_col = BLACK;cur->_left->_parent = parent;}delete cur;cur = nullptr;return true;}else if (cur->_col == RED){//判断为父亲节点的哪一边if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}//如果删除的单孩子节点为红色,直接删除delete cur;cur = nullptr;return true;}}else //双孩子节点{//如果删除节点为红色if (cur->_col == RED){Node* RightMinP = cur;Node* RightMin = cur->_right;while (RightMin && RightMin->_left){RightMinP = RightMin;RightMin = RightMin->_left;}cur->_data = RightMin->_data;//如果RightMin的颜色为黑色if (RightMin->_col == BLACK){//如果RightMin有右孩子,那么一定为红色的,删除RightMin之后要把他的右孩子变为黑色。if (RightMin->_right){RightMin->_right->_col = BLACK;RightMin->_right->_parent = RightMinP;// 如果有红色节点的uha,直接连接并且赋值为黑色if (RightMinP->_left == RightMin){RightMinP->_left = RightMin->_right;}else{RightMinP->_right = RightMin->_right;}delete RightMin;}else //如果没有的话那么转化为删除黑色叶子节点{ChangeColor(RightMin, RightMinP);if (RightMinP->_left == RightMin){RightMinP->_left = nullptr;}else{RightMinP->_right = nullptr;}delete RightMin;}return true;}else//如果RightMin的颜色为红色,直接删除,连接右孩子{if (RightMinP->_left == RightMin){RightMinP->_left = RightMin->_right;}else{RightMinP->_right = RightMin->_right;}if (RightMin->_right){RightMin->_right->_parent = RightMinP;}delete RightMin;return true;}}else//如果删除节点为黑色{Node* RightMinP = cur;Node* RightMin = cur->_right;while (RightMin && RightMin->_left){RightMinP = RightMin;RightMin = RightMin->_left;}cur->_data = RightMin->_data;//如果RightMin的颜色为黑色if (RightMin->_col == BLACK){if (RightMin->_right){//如果RightMin有右孩子,那么一定为红色的,删除RightMin之后要把他的右孩子变为黑色。RightMin->_right->_col = BLACK;RightMin->_right->_parent = RightMinP;if (RightMinP->_left == RightMin){RightMinP->_left = RightMin->_right;}else{RightMinP->_right = RightMin->_right;}delete RightMin;return true;}else //如果没有的话那么转化为删除黑色叶子节点{ChangeColor(RightMin, RightMinP);if (RightMinP->_left == RightMin){RightMinP->_left = nullptr;}else{RightMinP->_right = nullptr;}delete RightMin;}return true;}else//如果RightMin的颜色为红色,直接删除,连接右孩子{if (RightMinP->_left == RightMin){RightMinP->_left = RightMin->_right;}else{RightMinP->_right = RightMin->_right;}if (RightMin->_right){RightMin->_right->_parent = RightMinP;}delete RightMin;return true;}}}}}return false;
}
相关文章:

红黑树的插入与删除
文章目录 红黑树概念红黑树的性质: 红黑树的插入操作情况一情况二情况三 小总结红黑树的验证红黑树的删除一.删除单孩子节点1. 删除节点颜色为黑色2. 删除颜色为红色 二. 删除叶子节点1. 删除节点为红色2.删除节点为黑色2.1兄弟节点为黑色,有孩子节点&am…...
联通数科如何基于Apache DolphinScheduler构建DataOps一体化能力平台
各位小伙伴晚上好,我是联通数字科技有限公司数据智能事业部的王兴杰。 今天,我将和大家聊一聊联通数字科技有限公司是如何基于Apache DolphinScheduler构建DataOps一体化能力平台的。 今天的分享主要分为三个部分: 关于DataOps的一些思考&a…...

Python知识点:如何使用Mitmproxy进行HTTP/HTTPS流量分析
Mitmproxy 是一个强大的中间人代理工具,可以用来分析和修改 HTTP 和 HTTPS 流量。以下是如何使用 Mitmproxy 进行 HTTP/HTTPS 流量分析的步骤: 安装 Mitmproxy 首先,你需要在系统上安装 Mitmproxy。可以通过以下方式安装: 使用 …...

06:【stm32】OLED模块的简单使用
OLED模块的简单使用 OLED简单的使用 OLED简单的使用 OLED驱动函数是使用B站UP江科大的。我们直接调用即可,是使用软件模拟I2C协议进行通信的。具体的I2C协议可查看上官嵌入式开发中的C51单片机开发。 驱动函数文件:通过百度网盘分享的文件:…...

HIVE4.0.0的10000端口启动不起来的一种情况
问题 原生态部署HIVE4.0.0启动不起来10000端口,也没找到日志文件的位置,后来才知道日志文件默认在/tmp/<hostname>/路径下面,查看日志以为是Tez没安装的问题,我这儿要实现hive on spark,是不是该安装spark然后启…...

[极客大挑战 2019]FinalSQL1
打开题目 sql注入,点击1试一下 点击2试一下 点击3试一下 点击4 点击5 id6试一下 感觉是sql盲注了 编写脚本 import requests import string from time import sleep url "http://9da9cb18-3096-413a-9476-8a177ffec31a.node4.buuoj.cn:81/search.php?id0^(…...

Go语言 标签Label
Go语言 label标签和枚举介绍及使用示例 目录 标签label 标签和goto continue break 枚举 代码示例 说明 总结 标签label 标签和goto 设置标签,并在标签中判断符合条件后,跳到指定标签位置。 示例如下: package mainimport "…...

自反射 RAG 管道:如何实现?
什么是 Self-RAG? 人工智能中的自反射 RAG(检索增强生成)管道是指一种自适应和自我改进的系统,它结合了信息检索和语言生成过程,以提供更准确和特定于上下文的响应。这种类型的管道超越了标准的RAG 管道,它结合了一种自反射机制,使其能够评估其性能,确定需要改进的领域…...

怎么将jar注册为windows系统服务详细操作
将spring boot项目编译成jar,注册为windows系统服务 在网上了解到,winsw这个开源项目,去github看了下,作者常年维护更新,文档齐全,拥有不少,自己写了个小demo体验了下还不错,然后又运行了一个晚上,没啥问题,遂决定采用它 开源地址 源库地址 https://github.com/winsw/winsw R…...

数据结构.
1:基本大纲 数据结构、算法线性表:顺序表、链表、栈、队列树:二叉树、遍历、创建查询方法、排序方式 2:数据结构(逻辑结构,存储结构,操作(数据的运算)) 2.1:数据…...

thinkphp5之sql注入漏洞-builder处漏洞
目录 适用版本 环境搭建 文件下载安装 配置文件修改 漏洞分析 适用版本 注:thinkphp版本:5.0.13<ThinkPHP<5.0.15 、 5.1.0<ThinkPHP<5.1.5 环境搭建 文件下载安装 在github上面下载相应版本,下载think文件,…...

30集 如何编写ESP32程序接入AIGC实现更多有趣的功能-《MCU嵌入式AI开发笔记》
30集 如何编写ESP32程序接入AIGC实现更多有趣的功能(温度)-《MCU嵌入式AI开发笔记》 前言 之前我们建立了ESP-IDF和ESP-ADF开发环境,验证了硬件,验证了AI-CHAT的AI聊天工程,并且深入学习了cmake编译过程,…...

【JUC】Java对象内存布局和对象头
文章目录 面试题Object object new Object() 谈谈你对这句话的理解? 对象在堆内存中存储布局权威定义(周志明老师JVM第三版)对象在堆内存中的存储布局详解对象头的MarkWord源码对象标记源码 对象内存布局(使用JOL证明)…...

简单介绍一下css中transform的内容
在CSS中,transform属性用于对元素进行变换,包括旋转、缩放、倾斜和平移等操作。以下是transform属性中常用的属性: translate:用于元素的平移操作,可以指定元素在X轴和Y轴方向上的平移距离。 rotate:用于元…...

C 循环
C 循环 在C编程语言中,循环是一种控制结构,它允许我们重复执行一段代码多次。这是编程中非常基础且强大的功能,广泛应用于各种算法和数据处理的场景中。本文将详细介绍C语言中的循环概念,包括不同类型的循环语句及其使用方法。 …...

什么是设计模式?一文理解,通俗易懂!
前言 最近在学框架的时候,老师总是时不时带两句设计模式,什么工厂模式,单例模式,开发框架用到就提一嘴,但是没有细讲,为了搞懂啥是设计模式,为哈开发框架用到它,我就查找资料&#…...

doxygen制作接口文档
系列文章目录 文章目录 系列文章目录前言一、下载二、安装三、代码注释四、使用doxygen生成文档 前言 每次手动写接口文档太痛苦了,现在福利来了–doxygen Doxygen是软件开发中广泛使用的文档生成器工具。它自动从源代码注释生成文档,解析有关类、函数和…...

PDF怎么在线转Word?介绍四种转换方案
PDF怎么在线转Word?在数字化办公时代,文档的互换性变得尤为重要。PDF格式因其跨平台兼容性和版面固定性而广受欢迎,但有时我们可能需要将PDF文件转换为Word文档,以便进行编辑或进一步处理。以下是四种常见的在线PDF转Word的方法&a…...

大数据应用型产品设计方法及行业案例介绍(可编辑110页PPT)
引言:随着信息技术的飞速发展,大数据已成为推动各行各业创新与变革的重要力量。大数据应用型产品,作为连接海量数据与实际应用需求的桥梁,其设计方法不仅要求深入理解数据特性,还需精准把握用户需求,以实现…...
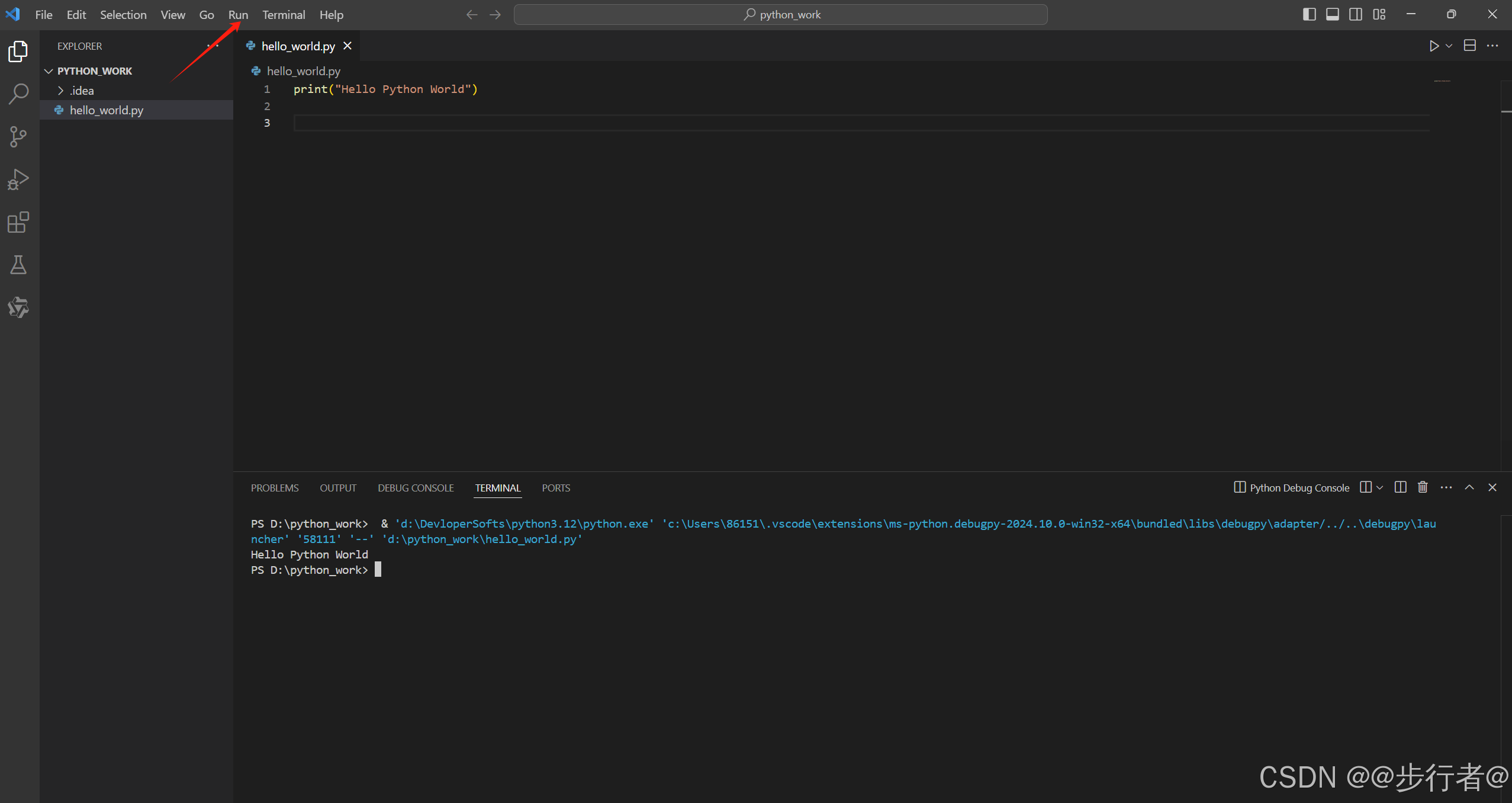
【Python零基础学习】Python环境安装和IDE选择
文章目录 前言一、Python介绍二、Python下载安装三、IDE选择VS CodePyCharm 四、打印Hello Python World使用cmd使用VS Code 总结 前言 本文是笔者学习Python语言的开篇文章了,Python语法相对比较简单,对编程初学者而言十分友好,应用极其广泛…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
