【动态规划算法题记录】343. 整数拆分 | 96.不同的二叉搜索树
整数拆分
题目🔗
题目描述
给定一个正整数 n ,将其拆分为 k个正整数的和(k >= 2),并使这些整数的乘积最大化。
返回你可以获得的最大乘积 。
思路分析
- dp数组含义:
dp[i]表示整数i拆分后的最大乘积。 - 递推公式:
dp[i] = j * dp[i - j] - dp数组初始化:
dp[0] = 0, dp[1] = 0, dp[2] = 1
cpp代码
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[0] = 0;dp[1] = 0;dp[2] = 1;for(int i = 3; i <= n; ++i){for(int j = 1; j <= i/2; ++j){dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));}}return dp[n];}
};
不同的二叉搜索树
题目🔗
题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
思路分析

- dp数组含义:
dp[i]表示由i个节点组成的不同二叉搜索树的数量。 - 递推公式:从上图我们可以发现,
dp[3] = 以1为头节点的二叉树数量+以2为头节点的二叉树数量+以3为头节点的二叉树数量
其中,
以1为头节点的二叉树数量 = 右子树有2个元素的搜索树数量 * 左元素有0个元素的搜索树数量
以2为头节点的二叉树数量 = 右子树有1个元素的搜索树数量 * 左元素有1个元素的搜索树数量
以3为头节点的二叉树数量 = 右子树有2个元素的搜索树数量 * 左元素有0个元素的搜索树数量
而,
有2个元素的搜索树数量 = dp[2]
有1个元素的搜索树数量 = dp[1]
有0个元素的搜索树数量 = dp[0]
因此可以推断出: d p [ i ] = d p [ j − 1 ] ∗ d p [ i − j ] dp[i] = dp[j - 1] * dp[i - j] dp[i]=dp[j−1]∗dp[i−j] - dp数组初始化:
dp[0] = 1
cpp代码
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0] = 1;for(int i = 1; i <= n; ++i){for(int j = 1; j <= i; ++j){dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};
总结
这两题都是属于思路比较绕,但想清楚之后会发现很简单的,所以前期一定要理解dp数组的相关含义。
相关文章:

【动态规划算法题记录】343. 整数拆分 | 96.不同的二叉搜索树
整数拆分 题目🔗 题目描述 给定一个正整数 n ,将其拆分为 k个正整数的和(k > 2),并使这些整数的乘积最大化。 返回你可以获得的最大乘积 。 思路分析 dp数组含义:dp[i]表示整数i拆分后的最大乘积。…...

网页上预览Excel文件
如何运行: 需要发布在服务器 如Tomcat 实例图片: 需要展示的文件: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>excel预览</title><link rel"stylesheet" href"…...

Unity射击游戏开发教程:(31)制造一定追踪行为的敌人
在本文中,我们将介绍如何在两种敌人行为之间切换。本文是前两篇文章的延续,分别介绍了敌人躲避玩家射击以及敌人不断旋转并向玩家射击的情况。我只是介绍如何在这两种行为之间进行转换。 这种新的敌人行为的目标: 当不开火时,敌人可以躲避玩家的射击。射击时,敌人无法躲避…...

springboot mybatis plus 固定查询条件及可选查询条件的组合查询,使用QueryWrapper.and()来解决。
1、我们在写查询SQL的时候,经常会碰到,比如,同一个类别下的某一个编号的物料信息,或者是同一批次的物料库存问题等等。 所属类别fid物料编号bm物料批次pc110.01.0220240807110.01.0320240807 210.02.0120240805 2、那么我…...

使用ollama取代openai的api进行graphRAG失败记录
pip install ollama pip install langchain_ollama graph_documents llm_transformer.convert_to_graph_documents(split_documents) print(graph_documents) 偶尔会成功,但是大部分是失败的: 报错记录如下,暂时没想到好的办法ÿ…...

MyBatis 配置与测试方式
目录 一,什么是MyBatis 二,准备工作 创建项目 配置数据库连接 持久层代码 单元测试 一,什么是MyBatis 简单来说,MyBatis 是一款优秀的持久层框架,用于简化JDBC的开发,能更简单完成程序与数据库之间…...

C#实现代理服务器
在C#中实现一个简单的代理服务器,可以使用System.Net.Sockets命名空间下的TcpListener类来监听客户端的连接请求,并使用TcpClient来处理与客户端的通信。以下是一个简单的代理服务器示例: using System; using System.IO; using System.Net;…...

react的路由实战使用
环境配置:vitetsreact18 1、安装包 npm i react-router-dom 2、 根路由配置以及路由挂载 a、在src下面创建router文件夹配置简单的路由信息: router/index.tsx import { createBrowserRouter } from "react-router-dom"; import UserLogin…...

python 字典转成类 构建类
目录 python 字典转成类 复杂嵌套示例: 动态实例化类 太好用了! python 字典转成类 class DictToClass:def __init__(self, dictionary):for key, value in dictionary.items():if isinstance(value, dict):# 如果值是字典,递归转换为类的实例setattr(self, key, DictToC…...

springboot 过滤器
1、过滤器的实现 springboot中过滤器通过实现接口Filter并重写init、doFilter、destroy三个方法。在三个方法中加入自己的业务逻辑处理。 【注意】Filter接口的完整包名在不同的jdk版中中的变化。这里示例中使用的版本为 open-jdk17。完整名称 jakarta.servlet.Filter。如果使…...

【C语言篇】深入理解指针1
文章目录 内存和地址内存编址 指针变量和地址取地址操作符指针变量和解引用操作符指针变量指针变量类型解引用操作符指针变量的大小 指针变量类型的意义指针的解引用指针-整数void*指针 const修饰指针指针运算指针-整数指针-指针指针的关系运算 野指针野指针成因如何规避野指针…...

IAP程序升级 与 电脑BIOS 的关系
IAP (In-Application Programming) 程序升级 IAP程序升级是一种技术,允许设备在运行过程中更新其自身的固件或软件,而不需要外部工具或设备的介入。这种技术特别适用于嵌入式系统和物联网(IoT)设备。其主要由三部分构成࿰…...

Java使用MQTT协议
MQTT(Message Queuing Telemetry Transport,消息队列遥测传输协议)是一种轻量级的、基于发布/订阅模式的物联网通信协议。它构建于TCP/IP协议之上,由IBM在1999年发布。MQTT的主要特点包括: 轻量级与高效:M…...

等级+时间的优先级算法
简介 本算法为等级与时间结合计算对应优先级逻辑 等级越高者优先级越高 同等级下,时间越小者优先级越高 实现 主方法 calculatePriority import com.zk.blog.enums.TypeEnum; import org.apache.commons.lang3.StringUtils;/*** program: * description:* autho…...

物流仓库安全视频智能管理方案:构建全方位、高效能的防护体系
一、背景分析 随着物流行业的快速发展和仓储需求的日益增长,仓库安全成为企业运营中不可忽视的重要环节。传统的人工监控方式不仅效率低下,且难以做到全天候、无死角覆盖,给仓库资产和人员安全带来潜在风险。因此,引入仓库安全视…...

jackson反序列化漏洞
jackson反序列化漏洞 反序列化漏洞触发根因jackson介绍jackson反序列化漏洞关键点enableDefaultTypingactivateDefaultTypingJsonTypeInfo 漏洞触发场景漏洞复现环境引入依赖pocactivateDefaultTypingenableDefaultTypingJsonTypeInfo 参考 很久没写blog,最近慢慢开…...

Java | Leetcode Java题解之第328题奇偶链表
题目: 题解: class Solution {public ListNode oddEvenList(ListNode head) {if (head null) {return head;}ListNode evenHead head.next;ListNode odd head, even evenHead;while (even ! null && even.next ! null) {odd.next even.nex…...

100 Exercises To Learn Rust 挑战!准备篇
公司内部的学习会非常活跃!我也参与了Rust学习会,并且一直在研究rustlings。最近,我发现了一个类似于rustlings的新教程网站:Welcome - 100 Exercises To Learn Rust。 rustlings是基于Rust的权威官方文档《The Rust Programming…...

瑞_RabbitMQ_初识MQ
文章目录 1 初识MQ1.1 同步调用1.1.1 同步调用的优势1.1.2 同步调用的缺点 1.2 异步调用1.2.1 异步调用的角色1.2.2 异步调用的优势1.2.3 异步调用的缺点1.2.4 异步调用的场景 1.3 MQ技术选型 2 RabbitMQ2.1 安装2.1.1 资源准备2.1.2 安装步骤 2.2 RabbitMQ架构2.3 RabbitMQ管理…...
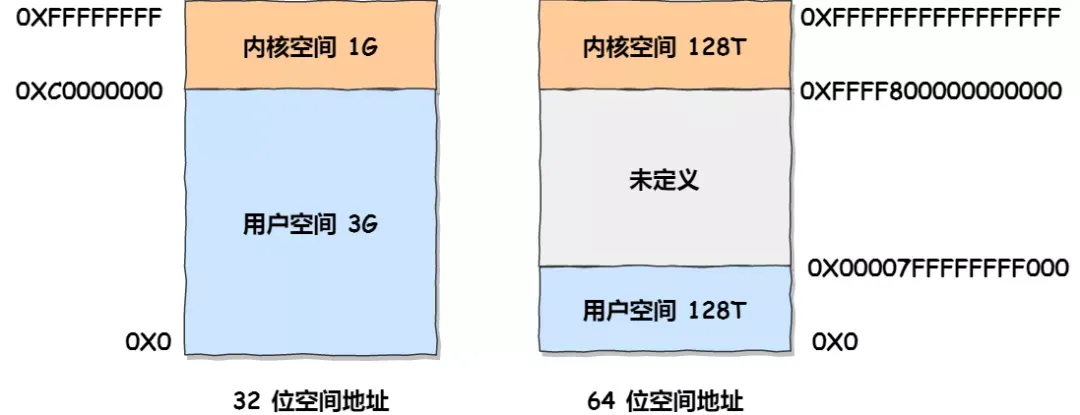
系统内存管理:虚拟内存、内存分段与分页、页表缓存TLB以及Linux内存管理
虚拟内存 虚拟内存是一种操作系统提供的机制,用于将每个进程分配的独立的虚拟地址空间映射到实际的物理内存地址空间上。通过使用虚拟内存,操作系统可以有效地解决多个应用程序直接操作物理内存可能引发的冲突问题。 在使用虚拟内存的情况下࿰…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
