Golang 并发编程

Golang 并发编程

Goroutine

什么是协程

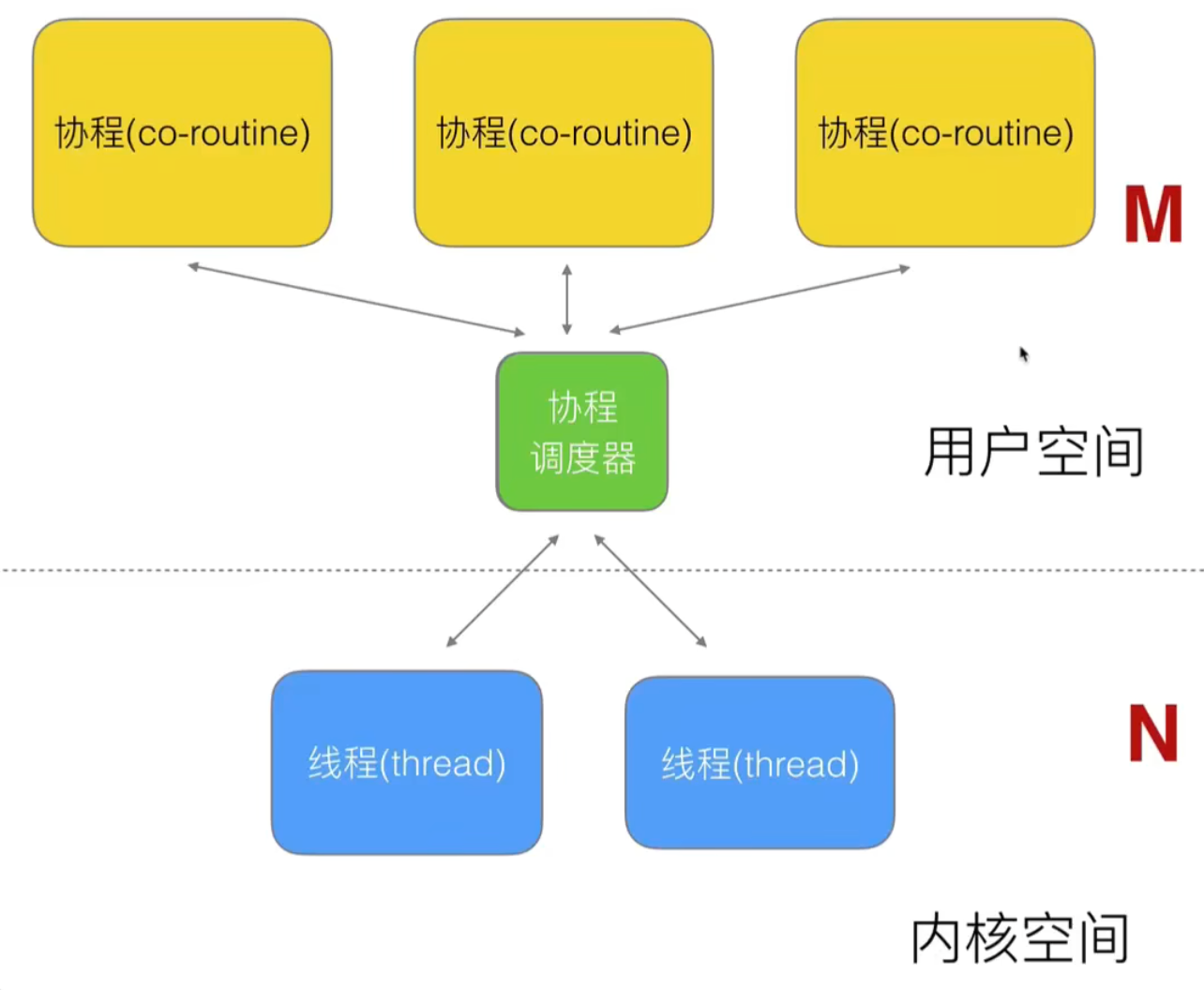
创建 Goroutine

主 goroutine （main函数）退出后，其它的工作 goroutine 也会自动退出

package mainimport ("fmt""time"
)func myFunc() {i := 0for {i++fmt.Println("func: ", i)time.Sleep(1 * time.Second)}
}func main() {go myFunc()i := 0for {i++fmt.Println("main: ", i)time.Sleep(1 * time.Second)}
}

main:  1
func:  1
func:  2
main:  2

Goexit 函数

调用 runtime.Goexit() 将立即终止当前 goroutine 执⾏

func myFunc() {i := 0for {i++fmt.Println("func: ", i)time.Sleep(1 * time.Second)if i == 10 {fmt.Println("func OVER ~")runtime.Goexit()}}
}func main() {go myFunc()i := 0for {i++fmt.Println("main: ", i)time.Sleep(1 * time.Second)}
}

...
func:  9
main:  9
main:  10
func:  10
func OVER ~
main:  11
main:  12
...

匿名函数

func main() {func() {fmt.Println("hello, I don't have name.")}()
}

func main() {fun := func() {fmt.Println("hello, I don't have name.")}fun()
}

Channel

什么是 Channel

channel 用来解决go程的同步问题以及go程之间数据共享（数据传递）的问题。

⽤类型 channel可用于多个 goroutine 通讯。其内部实现了同步，确保并发安全。

创建管道

package mainimport ("fmt""time"
)var c chan intfunc f(name string) {for {i := <-cfmt.Println(name, ": ", i)i++c <- itime.Sleep(1 * time.Second)}
}func main() {c = make(chan int)go f("fun1")go f("fun2")c <- 0for {}
}

fun2 :  0
fun1 :  1
fun2 :  2
fun1 :  3
fun2 :  4
fun1 :  5
fun2 :  6

Channel 的缓冲

无缓冲：通道不保存数据，生产者会等待消费者，将数据放到管道中。

有缓存：类似消息队列，可以保存在管道中。

package mainimport ("fmt""time"
)var c chan intfunc f(name string) {for {i := <-cfmt.Println(name, ": ", i)i++c <- itime.Sleep(10 * time.Millisecond)}
}func main() {// 有缓冲的 Channelc = make(chan int, 1)go f("fun1")go f("fun2")c <- 0time.Sleep(1 * time.Second)
}

会产生同一个 go 程会执行多次的效果

func main() {// 无缓冲的 Channelc = make(chan int)go f("fun1")go f("fun2")c <- 0time.Sleep(1 * time.Second)
}

两个 go 程交替运行，channel 作为锁，相互阻塞线程。

关闭 channel

package mainimport ("fmt"
)func main() {c := make(chan int)go func() {for i := 0; i < 5; i++ {c <- i}close(c)}()for {// ok为true说明channel没有关闭，为false说明管道已经关闭if data, ok := <-c; ok {fmt.Println(data)} else {break}}fmt.Println("Finished")
}

range 函数

可以用 range 迭代操作 channel

package mainimport ("fmt"
)func main() {c := make(chan int)go func() {for i := 0; i < 5; i++ {c <- i}close(c)}()for data := range c {fmt.Println(data)}fmt.Println("Finished")
}

select 函数

用于多路监控 channel

package mainimport ("fmt"
)func fibonacci(c, quit chan int) {x, y := 1, 1for {select {case c <- x:x, y = y, x+ycase <-quit:fmt.Println("quit")return}}
}func main() {c := make(chan int)quit := make(chan int)go func() {for i := 0; i < 6; i++ {fmt.Println(<-c)}quit <- 0}()fibonacci(c, quit)
}

Go Modules

配置

go env -w GO111MODULE=on
go env -w GOPROXY=https://goproxy.cn,direct

创建项目

go mod init github.com/wmh1024/demo_module
go get xxxx

replace

修改模块的版本依赖关系

go mod edit -replace=zinx@v0.0.0-20200306023939-bc416543ae24=zinx@v0.0.0-20200221135252-8a8954e75100