递归理解三:深度、广度优先搜索,n叉树遍历,n并列递归理解与转非递归
参考资料:
- DFS 参考文章
- BFS 参考文章
- DFS 参考视频
- 二叉树遍历规律
- 递归原理
- 源码
N叉树规律总结:
由前面二叉树的遍历规律和递归的基本原理,我们可以看到,二叉树遍历口诀和二叉树递推公式有着紧密的联系
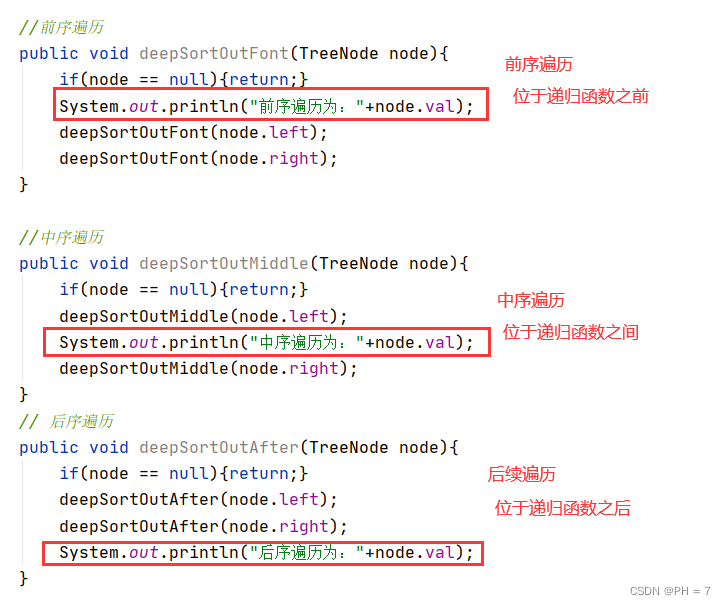
前序遍历:F(x) = op1(x) & F(x左) & F(x右) 口诀:根左右
中序遍历:F(x) = F(x左) & op1(x) &F(x右) 口诀:左根右
后序遍历:F(x) = F(x左) & F(x右) & op1(x) 口诀:左右根
其中op1(x)表示对数据X的操作
如果上述公式中,将op1(x)看做根,可以发现 递推公式和口诀是一摸一样的。
进而我们推断出,3叉树(3并列递归),4叉树(4并列递归)......乃至n叉树(n并列递归)规律都是这样的
3叉树(3并列递归)口诀
公式1:F(x) = op1(x) & F(x左) & F(x中) & F(x右) 口诀:根左中右
公式2:F(x) = F(x左) & op1(x) & F(x中) &F(x右) 口诀:左根中右
公式3:F(x) = F(x左)& F(x中) & op1(x) &F(x右) 口诀:左中根右
公式4:F(x) = F(x左)& F(x中) &F(x右) & op1(x) 口诀:左中右根
其中op1(x)表示对数据X的操作
4叉树(4并列递归)口诀
公式1:F(x) = op1(x) & F(x上) & F(x下) & F(x左) & F(X右) 口诀:根上下左右
公式2:F(x) = F(x上) & op1(x) & F(x下) & F(x左) & F(X右) 口诀:上根下左右
公式3:F(x) = F(x上) & F(x下) & op1(x) & F(x左) & F(X右) 口诀:上下根左右
公式4:F(x) = F(x上) & F(x下) & F(x左) & op1(x) & F(X右) 口诀:上下左根右
公式5:F(x) = F(x上) & F(x下) & F(x左) & F(X右) & op1(x) 口诀:上下左右根
其中op1(x)表示对数据X的操作
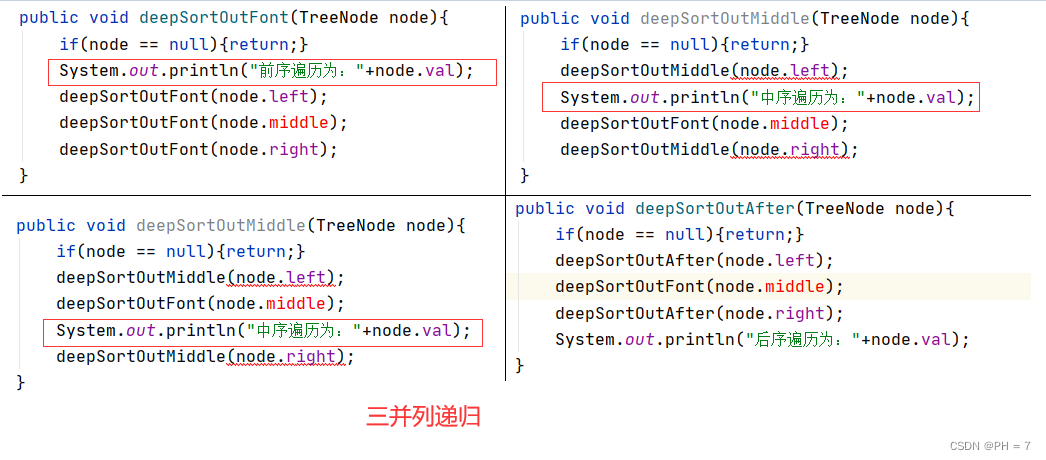
扩展至n叉树(n并列递归)口诀
公式1:F(x) = op1(x) & F(x属性1) & F(x属性2) & ......&F(x属性n)
口诀:根,属性1,属性2,......,属性n
N叉树规律验证:
由上述总结出的n叉树规律
公式1:F(x) = op1(x) & F(x属性1) & F(x属性2) & ......&F(x属性n)
口诀:根,属性1,属性2,......,属性n
我们用以下三叉树来进行验证,分别进行前中后序三种遍历
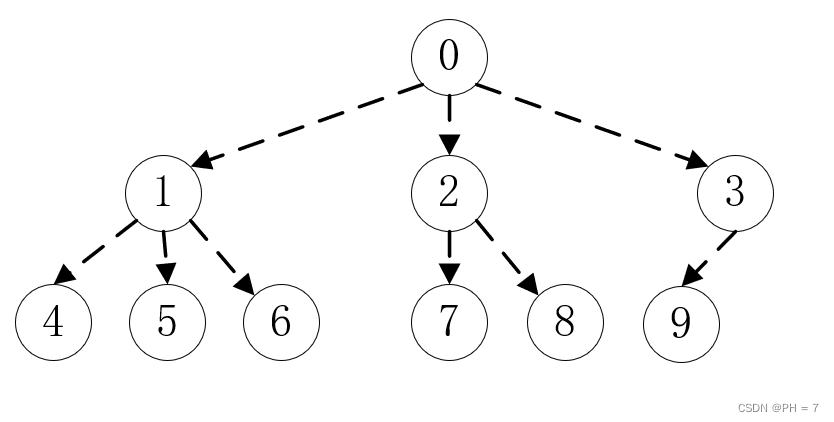
初始化语句:
//对三叉树进行初始化public TreeNode initNode(){// 先初始化最底层的TreeNode node9 = new TreeNode(9,null, null, null);TreeNode node8 = new TreeNode(8,null, null, null);TreeNode node7 = new TreeNode(7,null, null, null);TreeNode node6 = new TreeNode(6,null, null, null);TreeNode node5 = new TreeNode(5,null, null, null);TreeNode node4 = new TreeNode(4,null, null, null);TreeNode node3 = new TreeNode(3,node9, null, null);TreeNode node2 = new TreeNode(2,null, node7, node8);TreeNode node1 = new TreeNode(1,node4, node5, node6);TreeNode node0 = new TreeNode(0,node1, node2, node3);return node0;}- 前序遍历
根据代码:
public void deepSortOutFont(TreeNode node){if(node == null){return;}System.out.println("前序遍历为:"+node.val);deepSortOutFont(node.left);deepSortOutFont(node.middle);deepSortOutFont(node.right);}得到公式以及遍历口诀:
F(x) = op1(x) & F(x左) & F(x中) & F(x右) 口诀:根左中右
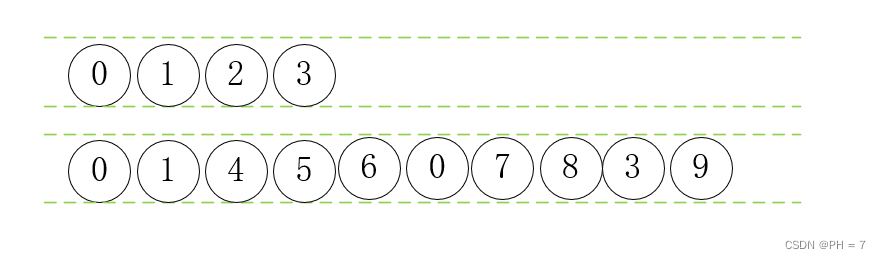
- 从根节点开始,根据口诀:根左中右,得到结果:0,1,2,3
- 以未遍历的节点1为根,根据口诀:根左中右,即1,4,5,6,得到结果:0,1,4,5,6,2,3
- 以未遍历的节点2为根,根据口诀:根左中右,即2,null,7,8,得到结果:0,1,4,5,6,2,7,8,3
- 以未遍历的节点3为根,根据口诀:根左中右,即3,9,null,null,得到结果:0,1,4,5,6,2,7,8,3,9
- 以未遍历节点4,5,6,7,8,9为根,根据口诀:根左中右,即n,null,null,null值不计,结果不变
- 所以根据递推公式总结的口诀:得到遍历结果为:,1,4,5,6,2,7,8,3,9
然后我们执行程序
@Testpublic void test(){//首先进行初始化TreeNode headNode = initNode();//深度优先遍历deepSortOutFont(headNode);//deepSortOutMiddle(headNode);//deepSortOutAfter(headNode);// 广度优先遍历//layerTranverse(headNode);}得到结果:

程序执行结果和口诀推导得到的结果一致,验证成功
总结:n项并列递归理解以及向非递归的转化:
- 根据代码总结出递推函数
对于一个n项递归函数,我们可以很轻易的写出他的递推函数,例如一个归并排序

mearge函数的意思是,将数组的left下标到right下标进行倒序排序,这里为了方便说明就不写出,文章后面会贴出完整代码
得到递推函数:
F(array,left,right) = op1 & F(array,left,middle) & F(array,middle,right) & op2
op表示数据操作,
F(array,left,middle) 为 F(array,left,right)的左半部分
F(array,middle,right) 为 F(array,left,right)的右半部分
- 根据递推函数得到遍历口诀
拆分公式,确保每一个公式只有一个op操作,并得到遍历口诀
F(array,left,right) = op1 & F(array,left,middle) & F(array,middle,right) 口诀:根左右
F(array,left,right) = F(array,left,middle) & F(array,middle,right) & op2 口诀:左右根
- 例举样本数据,从根节点开始,以未遍历的节点为根,按照遍历口诀,对各个节点进行排序
创建样本数据
array:{ 5, 4, 9, 8, 7, 6, 0, 1, 3, 2 }
left:0
right: 9
画出二叉树(当然三并列就是三叉树,n并列就是n叉树)
根据函数表述:两个递归函数是将数组的左半部分和右半部分不断分解,直到left>=right(注意终止条件不画出),得到如下二叉树
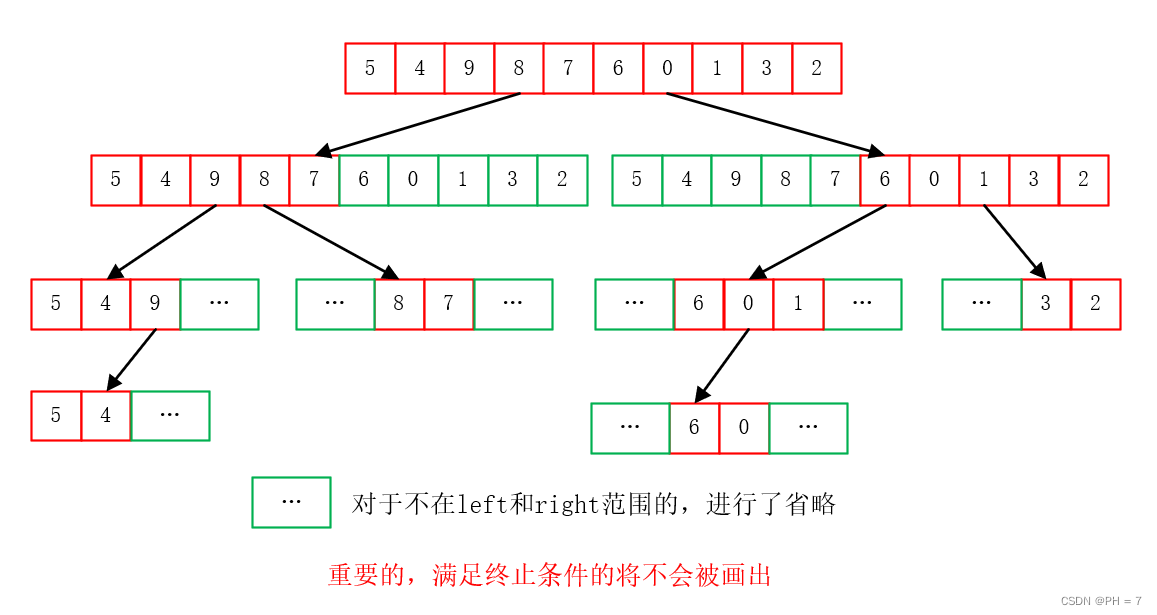
以第二个公式为例:
F(array,left,right) = F(array,left,middle) & F(array,middle,right) & op2 口诀:左右根
从根节点开始,根据:左右根口诀,得到merge函数的入参顺序,根据merge定义:将下标范围内的数字进行倒序排列,得到每一次入参后的结果
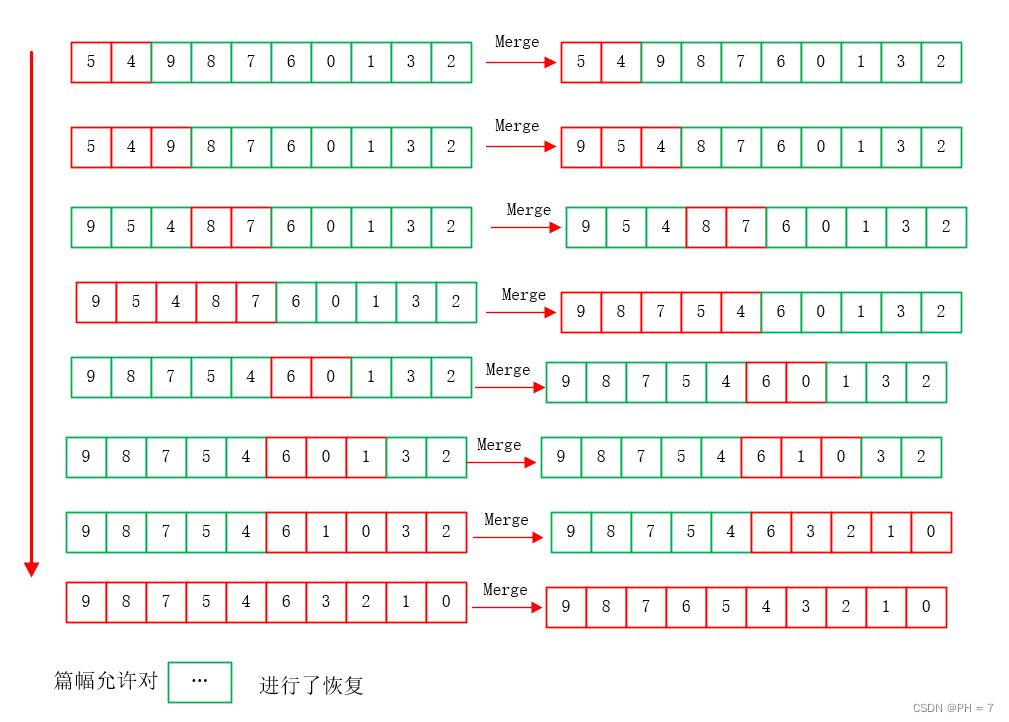
- 将排序后的数据依次作为数据操作函数的入参,归纳总结出该递推函数的作用
根据二叉树的分解以及执行流程,理解了此归并排序的含义:将数组不断地利用二分法进行分解,直至两个元素,然后再对每一部分进行排序
- 并且将循环套用的递归函数转化为了线性的,有多个入参的操作函数,且总结出递归函数的执行顺序
深度、广度优先遍历
其实,二叉树的深度,层级遍历,对应的就是简易的深度、广度优先遍历,见上一级
下面将简单介绍下他们在二维数组中的应用,以岛屿问题为例
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
深度优先遍历的解决办法是:详情见
void dfs(int[][] grid, int r, int c) {// 判断 base caseif (!inArea(grid, r, c)) {return;}// 如果这个格子不是岛屿,直接返回if (grid[r][c] != 1) {return;}grid[r][c] = 2; // 将格子标记为「已遍历过」// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}其实就是4并列递归
广度优先遍历的遍历方法为:详情见
// 网格结构的层序遍历
// 从格子 (i, j) 开始遍历
void bfs(int[][] grid, int i, int j) {Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{r, c});while (!queue.isEmpty()) {int n = queue.size();for (int i = 0; i < n; i++) { int[] node = queue.poll();int r = node[0];int c = node[1];if (r-1 >= 0 && grid[r-1][c] == 0) {grid[r-1][c] = 2;queue.add(new int[]{r-1, c});}if (r+1 < N && grid[r+1][c] == 0) {grid[r+1][c] = 2;queue.add(new int[]{r+1, c});}if (c-1 >= 0 && grid[r][c-1] == 0) {grid[r][c-1] = 2;queue.add(new int[]{r, c-1});}if (c+1 < N && grid[r][c+1] == 0) {grid[r][c+1] = 2;queue.add(new int[]{r, c+1});}}}
}
其实就是二叉树层级遍历的变形
相关文章:

递归理解三:深度、广度优先搜索,n叉树遍历,n并列递归理解与转非递归
参考资料: DFS 参考文章BFS 参考文章DFS 参考视频二叉树遍历规律递归原理源码N叉树规律总结: 由前面二叉树的遍历规律和递归的基本原理,我们可以看到,二叉树遍历口诀和二叉树递推公式有着紧密的联系 前序遍历:F(x…...
MATLAB 2023a安装包下载及安装教程
[软件名称]:MATLAB 2023a [软件大小]: 12.2 GB [安装环境]: Win11/Win 10/Win 7 [软件安装包下载]:https://pan.quark.cn/s/8e24d77ab005 MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。行矩阵运算、绘制函数和数据、实现算…...
QT学习开发笔记(数据库之实用时钟)
数据库 数据库是什么?简易言之,就是保存数据的文件。可以存储大量数据,包括插入数据、更 新数据、截取数据等。用专业术语来说,数据库是“按照数据结构来组织、存储和管理数据的 仓库”。是一个长期存储在计算机内的、有组织的、…...
Docker常规安装简介
总体步骤 搜索镜像拉取镜像查看镜像启动镜像,服务端口映射停止容器移除容器 案例 安装tomcat docker hub上面查找tomcat镜像,docker search tomcat从docker hub上拉取tomcat镜像到本地 docker pull tomcatdocker images查看是否有拉取到的tomcat 使用tomcat镜像创…...
Python - PyQT5 - ui文件转为py文件
在QTdesigner图形化编辑工具中,有些控件我们是可以直接在编辑界面进行编辑的,有些是不可以编辑的,只能通过Python代码进行编辑,不过总体来说,所有能够通过图形化编辑界面可以编辑的,都可以通过Python语言实…...

分布式事务和分布式锁
1、关于分布式锁的了解? 原理:控制分布式系统有序的去对共享资源进行操作,通过互斥来保持一致性。 具备的条件: ①分布式环境下,一个方法在同一时间只能被一个机器的一个线程执行 ②高可用的获取锁和释放锁 ③高性能…...
JAVA-4-[Spring框架]基于XML方式的Bean管理
1 Spring IOC容器 (1)IOC底层原理 (2)IOC接口(BeanFactory) (3)IOC操作Bean管理(基于XML) (4)IOC操作Bean管理(基于注释) 1.1 IOC概念 (1)控制反转(Inversion of Control),把对象的创建和对象之间的调用过程,交给Spring进行管理。 (2)使用IOC目的&…...
路科验证UVM入门与进阶详解实验0
一.代码编译 首先创建新项目,导入lab0 的UVM文件; 针对uvm_compile文件,先进行编译; module uvm_compile;// NOTE:: it is necessary to import uvm package and macrosimport uvm_pkg::*;include "uvm_macros.svh"in…...
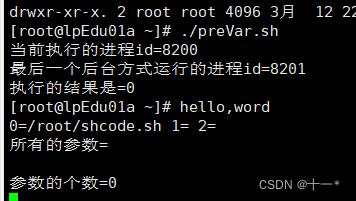
Linux之Shell编程(1)
文章目录前言一、Shell是什么二、Shell脚本的执行方式脚本的常用执行方式三、Shell的变量Shell变量介绍shell变量的定义四、设置环境变量基本语法快速入门五、位置参数变量介绍●基本语法●位置参数变量六、预定义变量基本介绍基本语法七、运算符基本介绍基本语法前言 为什么要…...
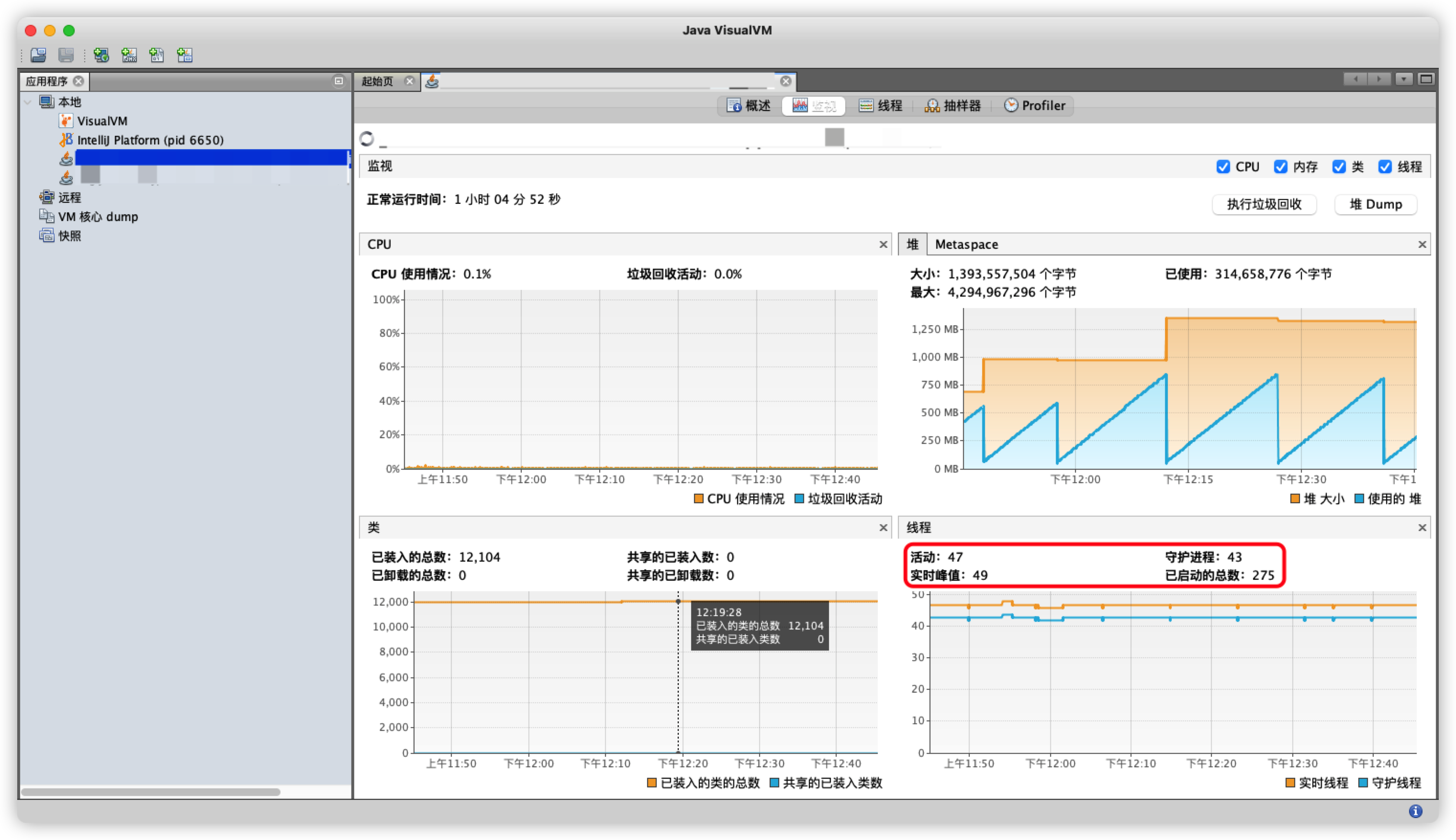
Java问题诊断工具——JVisualVM
这篇文章源自一次加班改bug的惨痛经历[,,_,,]:3负责的一个项目占用不断增加,差点搞崩服务器(╥﹏╥)……一下子有点懵,不能立刻确定是哪里导致的问题,所以决定好好研究下这个之前一直被我忽视的问题诊断工具🔧——JVisualVM嘿嘿我…...

Python3实现简单的车牌检测
导语Hi,好久不见~~~两周没写东西了,从简单的开始,慢慢提高文章水准吧,下一个月开始时间就会比较充裕了~~~利用Python实现简单的车牌检测算法~~~让我们愉快地开始吧~~~相关文件网盘下载链接: https://pan.baidu.com/s/1iJmXCheJoWq…...

基于支持向量机SVM多因子测量误差预测,支持向量机MATLAB代码编程实现
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 SVM应用实例,SVM的测量误差预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特…...

新农具时代,拼多多的进击与本分
这几年,乡村振兴被频频提及,核心就是经济振兴。但经济振兴,不能只靠政府,更要靠企业,政府引导、企业主导才能真正让农民、农村、农业长期受益。企业中,被寄予厚望的是电商企业。甚至,电商成为了…...
质量工具之故障树分析FTA(2) - FTA的基本概念
关键词:问题解决、故障树、故障树分析、FTA、可靠性、鱼骨图、根本原因分析 前文我们已经详细介绍了FTA的历史。 我们在工作中碰到一个问题,可以利用的问题解决工具有很多,故障树分析FTA就是其中之一。 但是FTA毕竟是相对复杂较难掌握的工具…...

《高质量C/C++编程》读书笔记二
文章目录前言三、命名规则四、表达式和基本语句if语句循环语句五、常量前言 这本书是林锐博士写的关于C/C编程规范的一本书,我打算写下一系列读书笔记,当然我并不打算全盘接收这本书中的内容。 良好的编程习惯,规范的编程风格可以提高代码…...

常用的美颜滤镜sdk算法
本文主要介绍常见的美颜滤镜SDK算法,包括 SRGB、 HSL、 Lab、 JPEG、 TIFF等。本文不会过多介绍算法原理,只是列举一些在实际项目中用到的滤镜效果,如: 1.色彩空间变换 2.颜色范围调节 3.色彩平衡调节 4.灰度级调节 5.色相/饱和度…...

动态SQL必知必会
动态SQL必知必会1、什么是动态SQL2、为什么使用动态SQL3、动态SQL的标签4、if 标签-单标签判断5、choose标签-多条件分支判断6、set 标签-修改语句7、foreach标签7.1 批量查询7.2 批量删除7.3 批量添加8、模糊分页查询1、什么是动态SQL 动态 SQL 是 MyBatis 的强大特性之一。如…...

DML编程控制
id生成策略 模型类: Data TableName("tbl_user") public class User {TableId(type IdType.AUTO)TableId(type IdType.NONE)TableId(type IdType.INPUT)TableId(type IdType.ASSIGN_ID)TableId(type IdType.ASSIGN_UUID)private Long id;private String name;T…...

关于肺结节实时的目标检测
目录 1. 对屏幕固定区域的检测 1.1 代码 1.2 结果展示 2. video 检测 2.1 代码 2.2 展示...
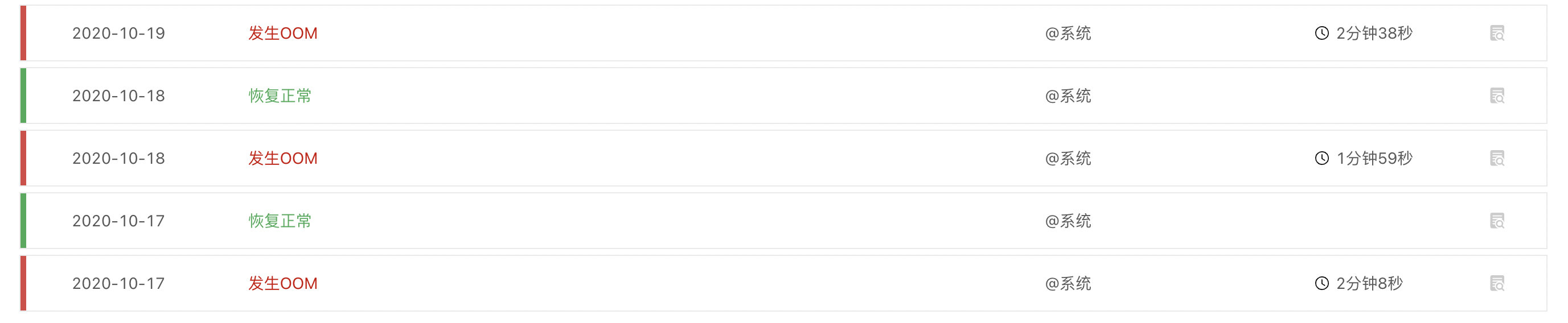
利用 Rainbond 云原生平台简化 Kubernetes 业务问题排查
Kubernetes 已经成为了云原生时代基础设施的事实标准,越来越多的应用系统在 Kubernetes 环境中运行。Kubernetes 已经依靠其强大的自动化运维能力解决了业务系统的大多数运行维护问题,然而还是要有一些状况是需要运维人员去手动处理的。那么和传统运维相…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
