算法学习day32
一、解码方法II(解码方法I的升级版)
在I的基础上增加了*,可以代替1-9中任意一个数字,求解码的方法有多少种
输入:s = "*" 输出:9 解释:这一条编码消息可以表示 "1"、"2"、"3"、"4"、"5"、"6"、"7"、"8" 或 "9" 中的任意一条。 可以分别解码成字符串 "A"、"B"、"C"、"D"、"E"、"F"、"G"、"H" 和 "I" 。 因此,"*" 总共有 9 种解码方法。
思路:
回顾一下上一题的思路:
1.如果遍历到的该位数字不是0,那么dp[i+1]=dp[i];
2.如果遍历到的数字可以和放一个数字构成一个有效的大写字母的ASCII值,是对dp[i+1]有用的,(这个有用是指多了dp[i-1]种分割方法)那么dp[i+1]+=dp[i-1];
那么这一道题的思路是?
1.如果遍历到的字符是*,
1.1 那么不论上一个字符是什么,首先dp[i+1]=dp[i]*9;
1.2 如果上一个字符是'1',那么dp[i+1]+=dp[i-1]*9
1.3 如果上一个字符是'2',那么dp[i+1]+=dp[i-1]*6(1->6)
1.4 其他情况均无法构成有效的大写字母
2.如果遍历到的字符不是'*'
2.1 如果不是0,那么就可以切割。dp[i+1]=dp[i];
2.2 如果上一个字符是'1',dp[i+1]+=dp[i-1]
2.3 如果上一个字符是'1',且当前的字符是'0'->'7',dp[i+1]+=dp[i-1]
2.4 如果上一个字符是'*',且当前字符是'0'->'7',dp[i+1]+=2*dp[i-1]
2.5 如果上一个字符是'*',且当前字符不是'0'->'7',dp[i+1]+=dp[i-1]
代码:
/*** 如果新加的一个字母是* 并且前一个数字是<=2的 直接+9* 前一个数字是*,直接+16* 解码方法I* 如果新加的数字可以和前面数字组成一个有效的大写字母 那么dp[i+1]=dp[i]+dp[i-1]* 如果不能组成dp[i+1]=dp[i]*/
class Solution {public int numDecodings(String s) {int mod = 1000000007;int size = s.length();long[] dp = new long[size + 1];dp[0] = 1;dp[1] = (s.charAt(0) == '*') ? 9 : 1;if (s.charAt(0) == '0')return 0;for (int i = 1; i < size; i++) {// 开始分情况if (s.charAt(i) == '*') {dp[i + 1] += dp[i] * 9;if (s.charAt(i - 1) == '1') {dp[i + 1] += dp[i - 1] * 9;} else if (s.charAt(i - 1) == '2') {dp[i + 1] += dp[i - 1] * 6;} else if (s.charAt(i - 1) == '*') {dp[i + 1] += dp[i - 1] * 15;}} else {if (s.charAt(i) != '0')dp[i + 1] = dp[i];if (s.charAt(i - 1) == '1')dp[i + 1] += dp[i - 1];else if (s.charAt(i - 1) == '2' && s.charAt(i) < '7')dp[i + 1] += dp[i - 1];else if (s.charAt(i - 1) == '*') {if (s.charAt(i) < '7')dp[i + 1] += 2 * dp[i - 1];elsedp[i + 1] += dp[i - 1];}}dp[i+1] %= mod;}return (int) dp[s.length()];}
}二、丑数II
给你一个整数 n ,请你找出并返回第 n 个 丑数 。丑数 就是质因子只包含 2、3 和 5 的正整数。
输入:n = 10 输出:12 解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
思路:
首先明白丑数的概念,质因子只包括2、3、5的正整数。因此可以推断出一个丑数必定是由x个2、y个3,z个5组成的。即n=2*x+3*y+5*z
那么我们如何寻找第n个丑数,可以使用数组,把n个丑数都求出来,那么如何判断第a个丑数是什么?
根据题目可知,1也是一个丑数,那么arr[0]=1;然后开始遍历:
arr[i]的值就从Math.min(arr[i2]*2,Math.min(arr[i3]*3,arr[i5]*5))中取
帮助理解:
现在丑数中有{1,2},在上一步中,1已经同2相乘过了,所以今后没必要再比较1×2了,我们说1失去了同2相乘的资格。
现在1有与3,5相乘的资格,2有与2,3,5相乘的资格,但是2×3和2×5是没必要比较的,因为有比它更小的1可以同3,5相乘,所以我们只需要比较1×3,1×5,2×2。
代码:
class Solution {public int nthUglyNumber(int n) {int[] dp=new int[n];dp[0]=1;int i2=0,i3=0,i5=0;for(int i=1;i<n;i++){dp[i]=Math.min(dp[i2]*2,Math.min(dp[i3]*3,dp[i5]*5));if(dp[i]==dp[i2]*2)i2++;if(dp[i]==dp[i3]*3)i3++;if(dp[i]==dp[i5]*5)i5++;}return dp[n-1];}
}三、超级丑数(类似于丑数II)
区别:
和丑数II的区别就是,丑数II的质因数只有2、3、5。而超级丑数的质因数的题目中给的。
思路:
使用一个map集合记录因数以及该因数参与的最近一次超级丑数的下标?
key:质因数
value:该因数参与的最近一次超级丑数的下标 类似于丑数II中的i2,i3,i5
dp[i]每次依然从dp[x]*primes[i]中选择一个最小的
代码:
class Solution {public int nthSuperUglyNumber(int n, int[] primes) {Map<Integer,Integer> map=new HashMap<>();for(int i:primes){map.put(i,0);}long[] dp=new long[n];dp[0]=1;for(int i=1;i<n;i++){Set<Integer> keys=map.keySet();long min=Long.MAX_VALUE;//找出最小值 也就是dp[i]放谁for(Integer key:keys){int value=map.get(key);if(dp[value]*key<min)min=dp[value]*key;}//找出最小值是由哪一个质数得到的 value+1for(Integer key:keys){int value=map.get(key);if(min/dp[value]==key)map.put(key,map.get(key)+1);}dp[i]=min;}return (int)dp[n-1];}
}四、青蛙过河(dp)
题意:给定一个数组stones[],代表每个单元格之间的距离,青蛙每次跳跃的距离是上一次跳跃的距离-1->+1;也就是在k-1,k,k+1这个范围中选择。
思路:
如何定义dp数组的含义:dp[i][j]代表的是能否从某个单元格跳j步到达i单元格。因此某个单元格一定是i之前的。那么根据j的不同,跳到i有很多种方法。
递推公式:dp[i][distance]=dp[j][distance-1]||dp[j][distance]||dp[j][distance+1]
如何理解这个递推公式:首先j是i之前的一个单元格,从j跳到i,要看distance是否满足我们能跳的距离。
如果上一个单元是跳了distance-1到达的,那么+1后可以得到distance;
如果上一个单元是跳了distance到达的,那么不变可以得到distance;
如果上一个单元是跳了distance+1到达的,那么-1可以得到distance;
代码:
class Solution {public boolean canCross(int[] stones) {int length=stones.length;//1.定义dp数组boolean[][] dp=new boolean[length][length];//dp数组的含义//初始化dp数组dp[0][0]=true;for(int i=1;i<length;i++){for(int j=i-1;j>=0;j--){int distance=stones[i]-stones[j];//如果此时的j是无法跳过来的,那么j--之后,更无法跳过来,所以直接breakif(distance>j+1)break;dp[i][distance]=dp[j][distance-1]||dp[j][distance]||dp[j][distance+1];if(i==length-1&&dp[i][distance])return true;}}return false;}
}五、等差数列划分(滑动窗口/dp)
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
输入:nums = [1,2,3,4] 输出:3 解释:nums 中有三个子等差数组:[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
解法一:滑动窗口
思路:
每次在数组中找一个最长等差数列,然后根据公式计算一下该等差数列中含有几个长度>=3的等差数列,如果len=5,长度为3的有3个,长度为4的有2个,长度为5的有1个。1+2+...+len-2 次数为:len-1 * len -2 /2
如果加上下一个元素 无法构成等差数列,那么就结算一下。然后继续重置数列长度。
代码:
/**
滑动窗口*/
class Solution {public int numberOfArithmeticSlices(int[] nums) {if(nums.length<3)return 0;int right=2;int count=0;int len=2;int preDiff=nums[1]-nums[0];while(right<nums.length){int curDiff=nums[right]-nums[right-1];if(curDiff==preDiff)len++;if(curDiff!=preDiff){count+=(len-1)*(len-2)/2;preDiff=curDiff;len=2;}right++;}count+=(len-1)*(len-2)/2;return count;}
}解法二:动态规划
思路:

dp[i]:代表以nums[i]为结尾的等差数列的个数。
如果nums[i]==nums[i-1]&&nums[i-1]==nums[i-2] 那么dp[i]+=dp[i-1]+1;
为什么dp[i]+=dp[i-1]+1,因为在原来的基础上延长到以nums[i]结尾的这个数列的长度是不变的,新加的+1是新组成的一个等差数列,由nums[i-2] nums[i-1] nums[i]组成
代码:
class Solution {public int numberOfArithmeticSlices(int[] nums) {if(nums.length<3)return 0;int[] dp=new int[nums.length];int res=0;for(int i=2;i<nums.length;i++){if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){dp[i]=dp[i-1]+1;res+=dp[i];}}return res;}
}相关文章:

算法学习day32
一、解码方法II(解码方法I的升级版) 在I的基础上增加了*,可以代替1-9中任意一个数字,求解码的方法有多少种 输入:s "*" 输出:9 解释:这一条编码消息可以表示 "1"、"…...

知识与智慧
前两天在medium上看到一篇文章,探讨知识(knowledge)和智慧(wisdom)之间的区别,很受启发,结合自己的经历和理解,形成此文: 何为知识 知识通常指的是信息的积累和对特定领…...
使用FFmpeg实现摄像头RTMP实时推流
在当今的数字时代,视频直播已成为连接人与人之间的重要桥梁,广泛应用于在线教育、远程会议、娱乐直播等多个领域。随着技术的不断进步,人们对于直播的实时性、稳定性和高质量需求日益增加。为了实现高效的视频直播,选择合适的工具和协议至关重要。 RTMP(Real-Time Messagi…...
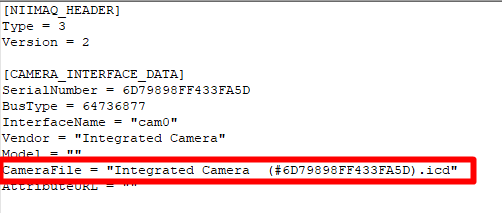
使用 LabVIEW 编程更改 IMAQ/IMAQdx 接口的相机文件
问题详情 可能需要通过编程方式更改与 IMAQ/IMAQdx 接口关联的相机文件。这种需求通常发生在图像采集系统中,例如使用 PCIe-1433 硬件时,可能需要动态切换不同的相机配置文件来适应不同的应用场景。 解决方案 当前在 Measurement & Automation Ex…...

[后端代码审计] PHP 基础学习
文章目录 前言1. 基础语法1 .1 注释1 .2 分隔符 2. 变量与常量2 .1 变量2 . 1 .1 变量定义2 . 1 .2 变量释放 2 .2 常量2 . 2 .1 常量定义2 . 2 .2 预定义常量 3. 运算符3. 1 算数运算符3 .2 字符串运算符3 .3 赋值运算符3 .4 比较运算符3 .5 逻辑运算符3 .6 其他运算符 4. 流程…...

【OpenCV C++20 学习笔记】直方图计算-split, calcHist, normalize
直方图计算-split, calcHist, normalize 广义直方图示例目标分离通道计算直方图绘制计算结果归一化绘制 最终结果 广义直方图 直方图的横坐标除了可以是图片中的强度值,也可以是任何其他我们想要观察的特征。例如,下面的图片矩阵中包含了0-255的强度值&…...

js入门经典学习小结
简介 js是解释型语言,虽然名字有java,但和java,c等编译型语言不同,它是解释型的,类似perl,py 历史 90年代最早js 1.0版本是网景navigator2引入的 然后欧洲计算机制造商协会(ECMA)…...
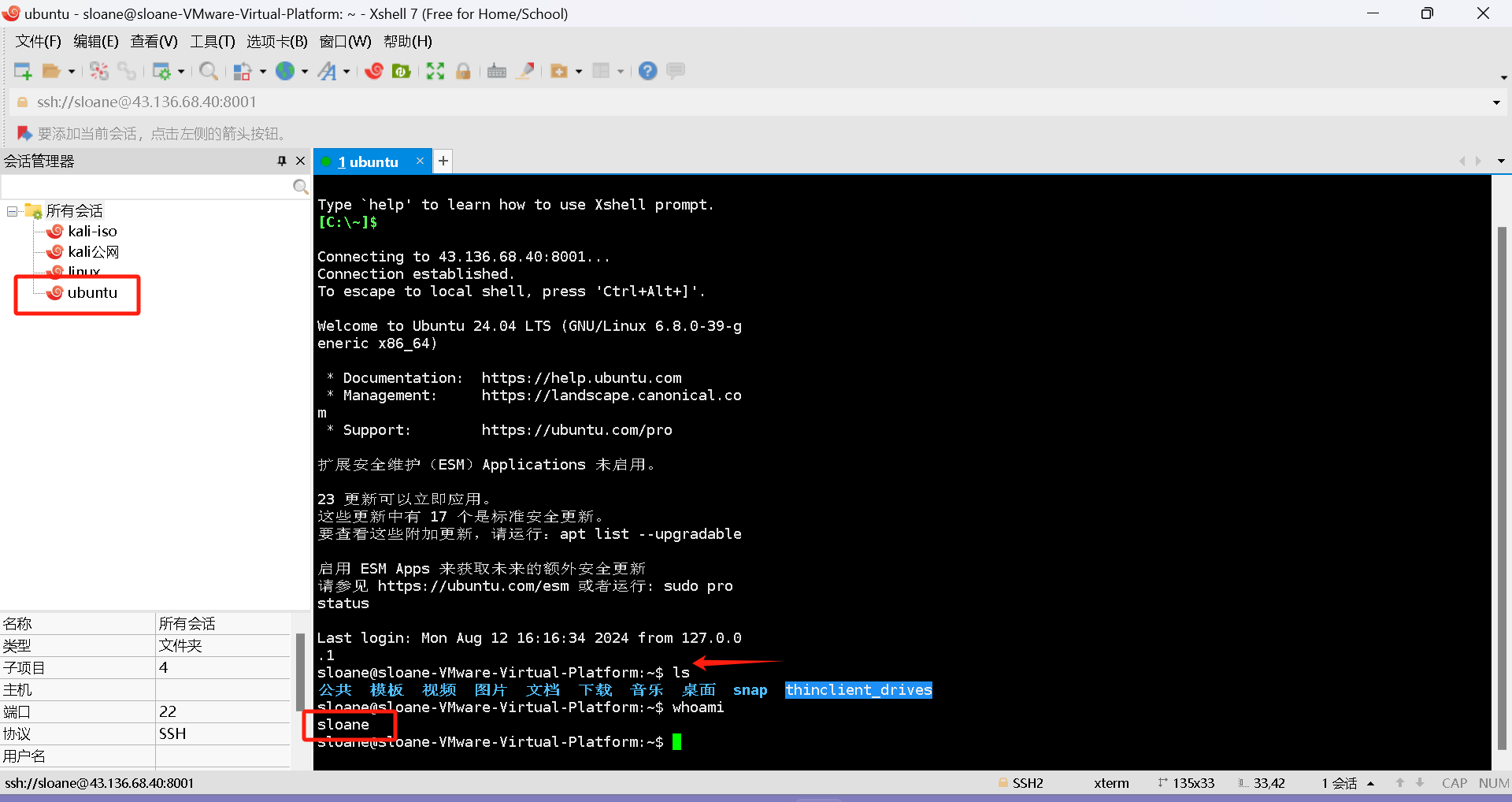
nps内网穿透之——腾讯云服务器和linux虚拟机
准备 1、客户端:准备一个内网的linux内网主机,或是一个虚拟机。 2、服务端:准备一个云服务器(阿里、腾讯、华为都行)。 安装方式: 1、自己到Github官网下载安装包上传。 下载地址:https://…...

大数据知识点
VMWare 设置网段 虚拟机设置 JDK部署 云平台 创建VPC 找到阿里云控制台里的VPC,点击专有网络 安全组 搁置…有需要再使用,因为每月要花200左右 大数据 数据导论...
)
【计算机毕设项目】2025级计算机专业项目推荐 (前后端Web项目)
以下项目选题适合计算机专业大部分专业,技术栈主要为:Java语言,SSMVue框架,MySQL数据库 后台免费获取源码,可提供远程调试、环境安装配置服务(文末有联系方式) 以下是本次部分项目推荐1-end&a…...

【MySQL】2.MySQL实际操作
目录 一、数据分析基本流程 注:Navicat快捷键 二、获取数据后的代码操作 (1)探索数据,查看定义 (2)筛选有用的字段 (3)建新表(查询建表插值 三合一) 注意…...

Winform画圆以及无边框窗体的移动
普通圆 在WinForms中绘制一个圆形,可以通过几种方式实现: 1. 使用ControlPaint类 在窗体的Paint事件中使用ControlPaint.DrawCircle方法来绘制圆形。 private void Form1_Paint(object sender, PaintEventArgs e) {int x 100; // 圆心的X坐标int y …...

如何高效记录并整理编程学习笔记?
高效记录并整理编程学习笔记是提升编程学习效率和效果的重要方法。以下是一些具体的步骤、工具及其使用方法的介绍: 一、高效记录笔记的方法 专注理解:在记录笔记时,首先要保持高度的专注,努力理解老师或教程中讲解的知识点。避免…...

docker的安装和常用命令
docker的安装和常用命令 安装老版本新版本 镜像源配置常用命令基本命令清理文件复制构建镜像上传镜像 补充权限不足无目录权限无用户权限 容器访问jenkins推送镜像失败修改主机名编写Dockerfile 注:这里的安装是针对于cetnos7。 安装 老版本 安装老版本可能遇到报…...

haproxy 7000字配图超详细教程 从小白到入门
简介:HAProxy是一个免费的负载均衡软件,可以运行于大部分主流的Linux操作系统上。HAProxy提供了L4(TCP)和L7(HTTP)两种负载均衡能力,具备丰富的功能。HAProxy的社区非常活跃,版本更新快速,HAProxy具备媲美商用负载均衡器的性能和稳…...
 的终极指南:5、将自然语言问题转换为结构化查询)
使用 LangChain 掌握检索增强生成 (RAG) 的终极指南:5、将自然语言问题转换为结构化查询
5. 查询构建 — Ragatouille 用户用自然语言提出问题并被路由到特定数据源(例如,向量存储、图形数据库等)后,该问题需要被转换为结构化查询,以便从选定的数据源检索信息(例如,文本到SQL、文本到…...

浅析JavaScript 堆内存及其通过 Chrome DevTools 捕获堆快照的方法
JavaScript 的堆内存(Heap Memory)是内存中专门用于存放程序执行过程中动态生成的对象、函数实例以及其他动态数据结构的区域。与调用栈(Call Stack)专注于管理函数调用的顺序和执行环境不同,堆内存则专注于动态地分配…...
----命名)
C++学习笔记----2、使用C++进行优雅编程(五)----命名
C编译器对于命名有如下规则: 命名中可以有大小写字母、数字、下划线。字母不限于英文字符,可以是任意国家语言的字母,例如日文,阿拉伯文等。不能以数字开头,例如9to5。包含双下划线的被标准库保留不可使用,…...

Element UI顶部导航栏与左侧导航栏联动实现~
需求:点击顶部导航栏的不同栏位实现左侧导航栏菜单的不同展示实现联动效果。 点击顶部导航栏按钮将对应的左侧导航栏数据传递给vuex,并在左侧导航栏父组件中接收并传递给左侧导航栏子组件,使用递归组件实现渲染等,具体的优化可以看下面的注释…...

ECMAScript6模板字面量:反引号、${}占位符的使用
ECMAScript 6 中引入了模板字面量,主要通过多行字符串和字符串占位符对字符串进行增强操作。如下: //使用ECMAScript6模板字面量拼接字符串,例如:2024年8月12日 15:38:28 星期一 let dateRet ${Year}年${Month}月${Dates}日 ${H…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
