算法刷题总结 (二) 回溯与深广搜算法
算法总结2 回溯与深广搜算法
- 一、理解回溯算法
- 1.1、回溯的概念
- 1.2、回溯法的效率
- 1.3、回溯法问题分类
- 1.4、回溯法的做题步骤
- 二、经典问题
- 2.1、组合问题
- 2.1.1、77. 组合 - 值不重复
- 2.1.2、216.组合总和III - 值不重复且等于目标值
- 2.1.3、17. 电话号码的字母组合 - 双层回溯
- 2.1.4、39. 组合总和 - 可复选同一值
- 2.1.5、40.组合总和II - 不可复选同一值,但有重复元素
- 2.1.6、练习
- 22. 括号生成
- 2.2、分割问题
- 2.2.1、131. 分割回文串 - 回溯附加条件
- 2.2.2、93.复原IP地址 - 回溯附加条件
- 2.3、子集问题
- 2.3.1、78. 子集 - 整棵遍历数
- 2.3.2、90. 子集 II - 乱序+重复元素+去重复值
- 2.4、排列问题
- 2.4.1、46.全排列
- 2.4.2、47.全排列 II
- 2.5、应用型类似问题
- 2.5.1、491.递增子序列 (和子集问题很像)- 非排序+重复元素+去重
- 2.5.2、332.重新安排行程(和2.1.3、17. 电话号码的字母组合 很像)
- 2.6、棋盘问题
- 2.6.1、HJ43 迷宫问题
- 2.6.2、51. N 皇后
- 2.6.3、37. 解数独
- 三、深搜DFS与广搜BFS
- 3.1、岛屿问题
- 200. 岛屿数量
- 1. 深度优先搜索DFS
- 2. 广度优先搜索 BFS
- 1254. 统计封闭岛屿的数目
- 1.深度优先搜索DFS
- 2.广度优先搜索
- 3.深度优先/广度优先 去除边界连通面积
- 1020.飞地的数量
- 695. 岛屿的最大面积
- 1.深度优先搜索DFS
- 2.广度优先搜索 BFS
- 1905. 统计子岛屿
- 130. 被围绕的区域
- 417. 太平洋大西洋水流问题
- 3.2、集合划分问题(等用于回溯的问题)
- 698. 划分为k个相等的子集
- 473. 火柴拼正方形
- 2305. 公平分发饼干
- 1723. 完成所有工作的最短时间
- 3.3、其他问题
- 547. 省份数量
- 参考

一、理解回溯算法
回溯与深广搜有相似的做法和理解,所以把他们放在同一个文章之中,文章看似篇幅很长,实际上,题目都是相似的,顺着章节来可以很快的掌握这个算法内容,以后碰到这样的相似题目,会很快想出思路。
1.1、回溯的概念
回溯是递归的纵横拓展,主要是递归(纵)+局部暴力枚举(横)。所以可以从递归和暴力两个方面来拆解回溯问题。
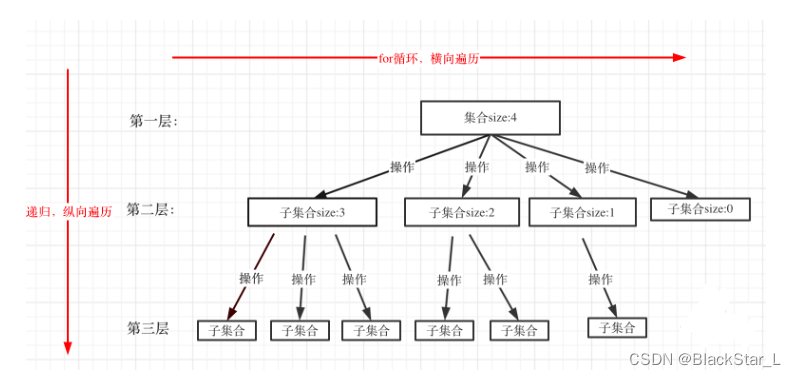
由上图可知,回溯法的所有问题都可以抽象为树形结构,集合的大小构成了树的宽度,递归深度构成了树的深度(N叉树)。因为递归有终止条件,所以树的高度会有限,同时递归的最终结果会呈现在叶子节点上。
1.2、回溯法的效率
从上一节的概念可知,回溯=递归+暴力搜索,所以它并不是一个特别高效的算法,即便再做一些剪枝优化下,依旧改变不了它的整体就是穷举的特性。
但即便这个算法效率不高,它的使用依旧很广泛,因为很多问题除了穷举,实在就是没有别的解决办法了,具体可以看看下一章的例题感受下。
1.3、回溯法问题分类
回溯法主要解决以下五种问题:
| 问题 | 描述 |
|---|---|
| 组合问题 | N个数里面按一定规则找出k个数的集合 |
| 切割问题 | 一个字符串按一定规则有几种切割方式 |
| 子集问题 | 一个N个数的集合里有多少符合条件的子集 |
| 排列问题 | N个数按一定规则全排列,有几种排列方式 |
| 棋盘问题 | N皇后,解数独,迷宫等等 |
1.4、回溯法的做题步骤
回溯法三部曲:
- 回溯函数的模板,返回值以及参数
这里回溯函数起名为backtracking,回溯算法中函数返回值一般为空。
对于参数的话,很难提前确定下来,一般是先写逻辑,然后需要什么参数,就填什么参数。
def backtracking(参数):
- 回溯函数终止条件
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
if 终止条件:保存结果return
- 回溯搜索的遍历过程
# 横向遍历。一个节点有多少个孩子就执行多少次
for i in [本层集合中的元素(树中及节点孩子的数量就是集合的大小)]:处理节点# 纵向遍历,自己调用自己实现递归backtracking(路径,选择列表)回溯,撤销处理结果
总结:
def backtracking(参数):if 终止条件:存放结果returnfor i in [本层集合中的元素(树中及节点孩子的数量就是集合的大小)]:处理节点# 纵向遍历,自己调用自己实现递归backtracking(路径,选择列表)回溯,撤销处理结果
二、经典问题
2.1、组合问题

2.1.1、77. 组合 - 值不重复
力扣题目链接
1.使用函数:
itertools库下的combinations组合函数,与之对应的是permutations排列函数。
from itertools import combinations
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:l = [i+1 for i in range(n)]res = combinations(l, k)return list(res)
2.回溯法:
从题目可以知道,k=2两层循环解决,k=3三层循环,但是题目的k是变动的,也就是for循环的层数是需要是变动的,那么回溯法就用递归来解决层数嵌套,每递归一次就是一层for循环,一个简单的过程如下:
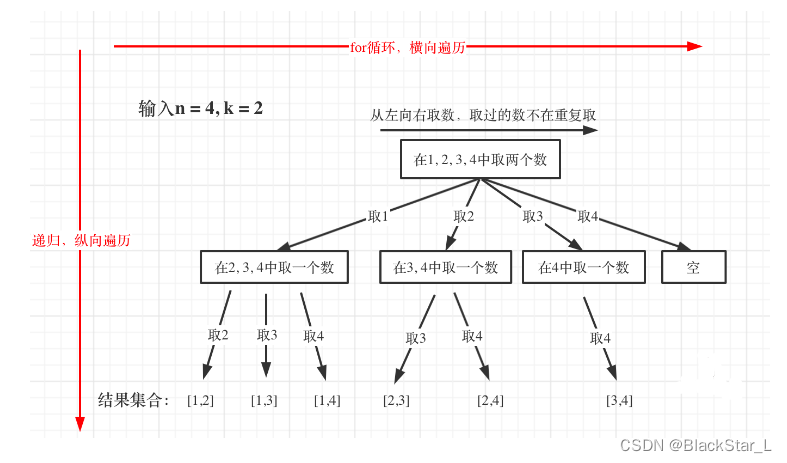
n相当于树的宽度,k相当于树深度的
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:# 存放符合条件结果的集合result = []# 存放符合条件单一结果path = []# startIndex来记录下一层递归,搜索的起始位置def backtracking(n, k, startIndex):if len(path)==k:# 这里注意要添加一个path的拷贝,直接append为原址# path最后会被pop,结果为空值result.append(path[:])returnfor i in range(startIndex, n+1):path.append(i)backtracking(n, k, i+1)path.pop()backtracking(n, k, 1)return result加上剪枝操作(当path为固定长度时):
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。那么后面这些部分可以剪掉,如下,只用更改循环的终止条件改变范围就行。
# 这里
# n - (k-len(path))+1恰好满足最后一个长度到结尾
# 再往右就不满足了
# n = 4, k = 2, 当len(path) = 1 时
# 4 - (2 - 1) +1 = 4,从startindex到4都是可以取的
endIndex = n - (k-len(path))+1
for i in range(startIndex, endIndex+1):path.append(i)backtracking(n, k, i+1)path.pop()
当然,这个剪枝是针对,有固定长度k才可取。
综上为:
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:# 存放符合条件结果的集合result = []# 存放符合条件单一结果path = []# startIndex来记录下一层递归,搜索的起始位置def backtracking(n, k, startIndex):if len(path)==k:result.append(path[:])return# n = 4, k = 2, 当len(path) = 1 时# 4 - (2 - 1) +1 = 4,从startindex到4都是可以取的endIndex = n - (k-len(path))+1for i in range(startIndex, endIndex+1):path.append(i)backtracking(n, k, i+1)path.pop()backtracking(n, k, 1)return result2.1.2、216.组合总和III - 值不重复且等于目标值
力扣题目链接
1.使用函数:
from itertools import combinations
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:res = []l = combinations([i+1 for i in range(9)], k)for i in list(l):if sum(i)==n:res.append(i)return res
2.回溯搜索:
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:res = []path = []def backtracking(ind):if len(path)==k:if sum(path)==n:res.append(path[:])return# 剪枝1,同前面的原理endindex = 9-(k-len(path))+1for i in range(ind, endindex+1):path.append(i)# 剪枝2,和大了就不继续回溯,这个放前面,backtracking下第一行也行if sum(path)<=n:backtracking(i+1)path.pop()backtracking(1)return res
加上两次剪枝:
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:path = []res = []def backtracking(k, n, startIndex):# 剪枝1,大于目标值,再遍历也没意义,直接去掉if sum(path)>n:returnif len(path)==k and sum(path)==n:res.append(path[:])return# 剪枝2,需要搭配剪枝1,否则k-len(path)会为负数,循环次数反而会增加endIndex = 9 - (k-len(path))+1for i in range(startIndex, endIndex+1):path.append(i)backtracking(k, n, i+1)path.pop()backtracking(k, n, 1)return res
本题与77.组合 加了元素总和的限制,同样的,把问题抽象为树形结构,按照回溯算法的步骤走,最后给出剪枝的优化。

2.1.3、17. 电话号码的字母组合 - 双层回溯
力扣题目链接
回溯法1,从digits的角度:
class Solution:def letterCombinations(self, digits: str) -> List[str]:d = {'2':'abc', '3':'def', '4':'ghi', '5':'jkl', '6':'mno', '7':'pqrs','8':'tuv','9':'wxyz'}# 存储根节点path = []# 存储最终结果res = []# 回溯数字def backtracking(digits):if len(digits)==0:# 去除空值,非空则添加字符串if path:res.append(''.join(path[:]))return# 循环取一个数字对应的字母for i in d[digits[0]]:# 存一个该数字的字母path.append(i)# 去除第一个数字,后面的数字串backtracking(digits[1:])path.pop()backtracking(digits)return res
回溯法2:从index的角度:
class Solution:def letterCombinations(self, digits: str) -> List[str]:alphas = {"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs","8":"tuv","9":"wxyz"}path = []res = []def backtracking(ind):if len(path)==len(digits):if path:res.append(''.join(path[:]))returnfor a in alphas[digits[ind]]:path.append(a)backtracking(ind+1)path.pop()backtracking(0)return res
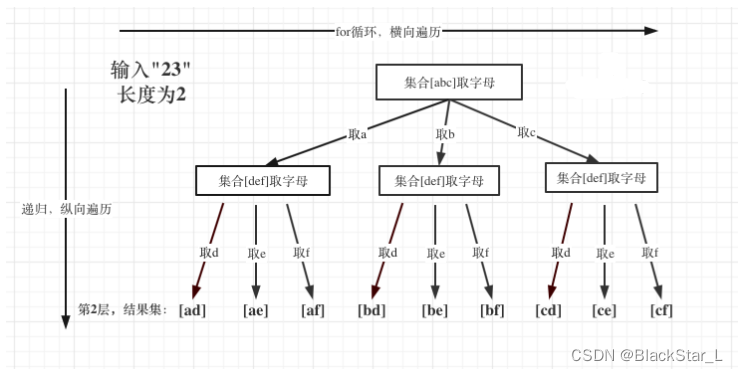
注意:输入1 * #按键等等异常情况。代码中最好考虑这些异常情况,但题目的测试数据中应该没有异常情况的数据,但是要知道会有这些异常,如果是现场面试中,就一定要考虑到。
2.1.4、39. 组合总和 - 可复选同一值
力扣题目链接
回溯法1,candidates角度:
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []def backtracking(candidates):# 大于目标值直接返回空if sum(path)>=target:if sum(path)==target and sorted(path) not in res:# 值存进去之前,提前排序,便于去重res.append(sorted(path[:]))return# 循环整个列表(注意这里会产生重复结果,只是顺序不同)for i in candidates:path.append(i)backtracking(candidates)path.pop()backtracking(candidates)return res
回溯法2,index角度:
这里加上循环的起始索引,并引入一个su_m变量去存储每一步的sum。
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []def backtracking(candidates, su_m, startIndex):# 因为循环进行了优化,所以这里判断会简单许多if su_m>=target:if su_m==target:res.append(path[:])return# [2,3,5,7], 7# 这种循环索引而不是列表值,会优先考虑重复# 所以不会出现[2,3,2]和[3,2,2]这种重复的排列# 优先[2,2,2,2]得不到target开始popfor i in range(startIndex, len(candidates)):su_m += candidates[i]path.append(candidates[i])# 这里起始索引为i,因为可以重复使用backtracking(candidates, su_m, i)# 回溯要减去值su_m -= candidates[i]path.pop()backtracking(candidates, 0, 0)return res
这里还可以简化下:
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:res = []path = []def backtracking(ind):if sum(path)==target:res.append(path[:])returnfor i in range(ind, len(candidates)):path.append(candidates[i])if sum(path)<=target:backtracking(i)path.pop()# 这里直接一个index即可backtracking(0)return res
回溯1会产生排列,要去重,而回溯2只产生组合。
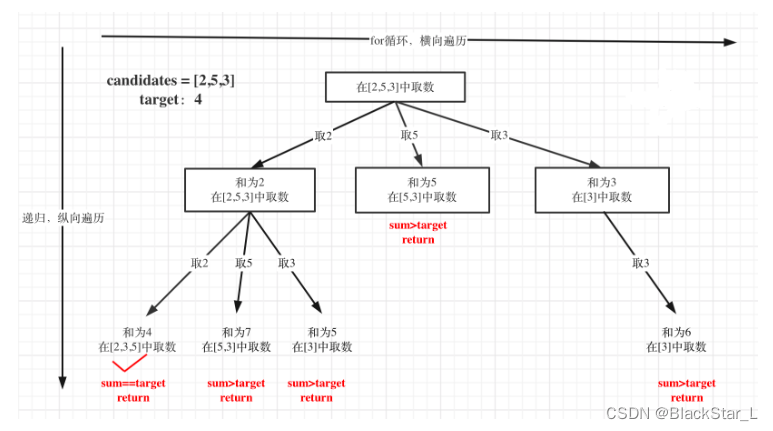
剪枝优化:
当判断sum > target后,就没有必要进入下一层递归。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
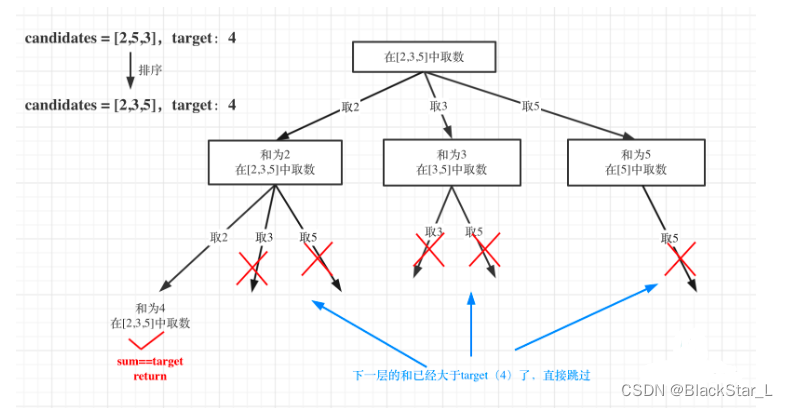
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []def backtracking(candidates, su_m, startIndex):if su_m==target:res.append(path[:])returnfor i in range(startIndex, len(candidates)):# 排序后,小的值的和都大于target,后续大的无序继续# 不排序,结果会出问题if su_m + candidates[i]> target:returnsu_m += candidates[i]path.append(candidates[i])backtracking(candidates, su_m, i)su_m -= candidates[i]path.pop()# 注意要排序candidates.sort()backtracking(candidates, 0, 0)return res
2.1.5、40.组合总和II - 不可复选同一值,但有重复元素
力扣题目链接
本题的难点在于:集合(数组candidates)有重复元素,但还不能有重复的组合。
回溯法1(超时):
把所有组合求出来,去除重复的。
class Solution:def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []def backtracking(candidates, su_m, startIndex):# 这里会有重复的,如[1,1,2,5,6,7,10],8# 第一个1与第二个1意义不同,[1,2,5] 和 [1,2,6], [1,7]和[1,7]# 但对结果来说相同。if su_m == target and path[:] not in res:res.append(path[:])return for i in range(startIndex, len(candidates)):if su_m + candidates[i]>target:returnsu_m += candidates[i]path.append(candidates[i])backtracking(candidates, su_m, i+1) su_m -= candidates[i]path.pop()candidates.sort()backtracking(candidates, 0, 0)return res
这里会有重复的,如[1,1,2,5,6,7,10],8。
第一个1与第二个1意义不同,[1,2,5] 和 [1,2,6], [1,7]和[1,7],但对结果来说相同。
所以,只需要第一次的1就可以,同一树层,第一次出现的重复元素会遍历到后面的重复元素,记一次就行,树层的其他相同的直接去掉。
把所有组合求出来,再去重,这么做很容易超时,所以要在搜索的过程中就去掉重复组合。
回溯法2(使用startIndex去重):
既然求结果去重会超时,那么就需要在求的过程中提前去重。
这里直接使用startIndex进行判断去重,同一个树层(for循环内)和上一个元素相等则continue跳过。
class Solution:def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []def backtracking(startIndex):# 这里会有重复的,如[1,1,2,5,6,7,10]# 第一个1与第二个1意义不同,但对结果来说相同if sum(path) == target:res.append(path[:])return for i in range(startIndex, len(candidates)):# 只是用索引来判断重复。这里注意不是i>0# 因为每一层的元素有更新,得从startIndex开始# 否则i>0则不存在重复元素了if i>startIndex and candidates[i] == candidates[i-1]:continuesu_m += candidates[i]path.append(candidates[i])if sum(path)<=target:backtracking(i+1) su_m -= candidates[i]path.pop()candidates.sort()backtracking(0)return res
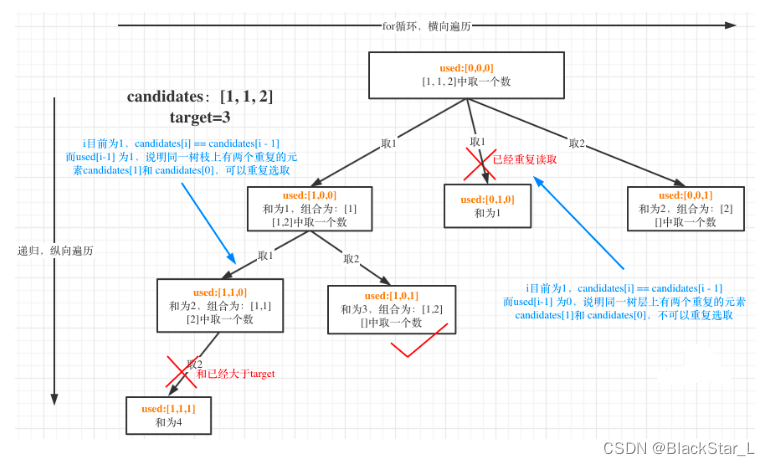
回溯法3(新建used数组去重):
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过,纵向
used[i - 1] == false,说明同一树层candidates[i - 1]使用过,横向
class Solution:def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:path = []res = []used = [False] * len(candidates)def backtracking(startIndex):# 这里会有重复的,如[1,1,2,5,6,7,10]# 第一个1与第二个1意义不同,但对结果来说相同if sum(path) == target:res.append(path[:])return for i in range(startIndex, len(candidates)):# 上个相同节点没使用过,为False,可以判断为同一树层,则跳过# 上个相同节点使用过,为True,可以判断为同一树枝,不跳# 这里注意不同于前面i>startIndex# 本来i>0不允许任何重复,但used[i-1]==False,表示同一层,从这个相同点开始,(前面一个相同点已经回溯成False了)if i>0 and candidates[i] == candidates[i-1] and used[i-1]==False:continueused[i]=Truepath.append(candidates[i])if sum(path)<=target:backtracking(i+1) # 回溯,为了下一轮for loop used[i]=Falsesu_m -= candidates[i]path.pop()candidates.sort()backtracking(0)return res
2.1.6、练习
22. 括号生成
22. 括号生成
class Solution:def generateParenthesis(self, n: int) -> List[str]:res = []path = []def backtracking(l, r):if l==n and r==n:res.append(''.join(path))if l<n:path.append('(')backtracking(l+1,r)path.pop()if r<l:path.append(')')backtracking(l,r+1)path.pop()backtracking(0,0)return res

2.2、分割问题
2.2.1、131. 分割回文串 - 回溯附加条件
力扣题目链接
回溯+双指针:
class Solution:def partition(self, s: str) -> List[List[str]]:res = []path = []# 判断回文的函数# 正反序
# def isPalindrome(s, start, end):
# if s[start:end+1] == s[start:end+1][::-1]:
# return True
# return False# 双指针def isPalindrome(s, start, end):while start<end:if s[start] != s[end]:return Falsestart+=1end-=1return Truedef backtracking(s, startIndex):if startIndex>= len(s):res.append(path[:])returnfor i in range(startIndex, len(s)):# 判断是否为回文,是再添加到path# 不是回文,则切割失败,后续操作跳过if isPalindrome(s, startIndex, i):path.append(s[startIndex:i+1])else:continuebacktracking(s, i+1)path.pop()backtracking(s, 0)return res
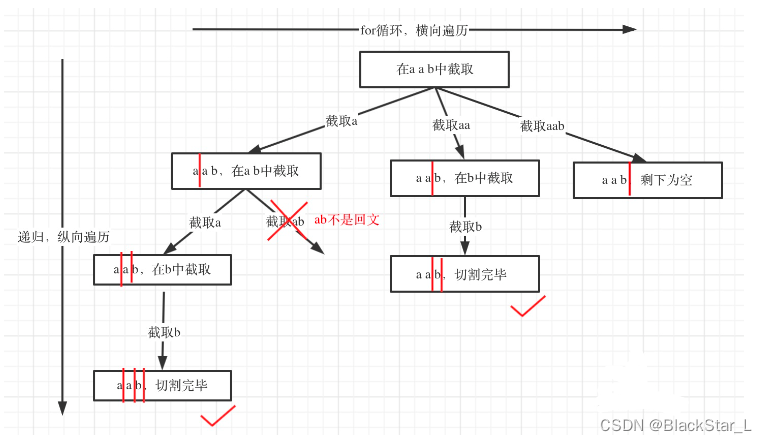
回溯+正反序:
class Solution:def partition(self, s: str) -> List[List[str]]:res = []path = []def backtracking(ind):if ind==len(s):res.append(path[:])for i in range(ind, len(s)):if s[ind:i+1]!=s[ind:i+1][::-1]:continuepath.append(s[ind:i+1])backtracking(i+1)path.pop()backtracking(0)return res

2.2.2、93.复原IP地址 - 回溯附加条件
力扣题目链接
回溯法1, 使用index:
思路同上一题,切割成4份为终止标准,结合startIndex判断是否遍历完整字符串,将合法的结果用’.'拼接即可。
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:res = []path = []# 判断是否合法# 1. 0-255 之间,闭区间# 2. 当长度大于1时(或不为0),首位不能为0def isValid(s, start, end):if 0<=int(s[start:end+1])<=255 and \(s[start:end+1]=='0' or s[start:end+1].lstrip('0')==s[start:end+1]):# 首位不能为0,则去除首位的0后还是原来的字符串则首位无0return Truereturn Falsedef backtracking(startIndex):# 终止条件为截取了4段if len(path)==4:# 截取4段,并且索引到了尾部,即取了所有字符if startIndex == len(s):# 将结果用.拼接起来res.append('.'.join(path[:]))return # 遍历字符串for i in range(startIndex, len(s)):if isValid(s, startIndex, i) and len(path)<=4:path.append(s[startIndex:i+1])backtracking(i+1)path.pop()backtracking(0)return res
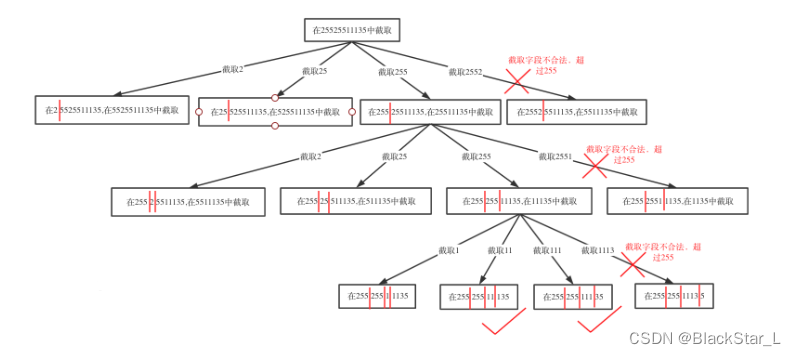
回溯法2,使用string:
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:res=[]path=[]def isvalid(string):if len(string)==len(str(int(string))) and 0<=int(string)<=255:return Truereturn Falsedef dfs(s):if len(path)==4 and s:return Falseif len(path)==4 and not s:res.append('.'.join(path[:]))returnfor i in range(len(s)):if isvalid(s[:i+1]):path.append(s[:i+1])dfs(s[i+1:])path.pop()dfs(s)return res

2.3、子集问题
2.3.1、78. 子集 - 整棵遍历数
力扣题目链接
注:幂集就是集合的所有子集。
回溯法:
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(nums, startIndex):# 子集就是遍历整个树res.append(path[:])if startIndex == len(nums):returnfor i in range(startIndex, len(nums)):path.append(nums[i])backtracking(nums, i+1)path.pop()backtracking(nums, 0)return res
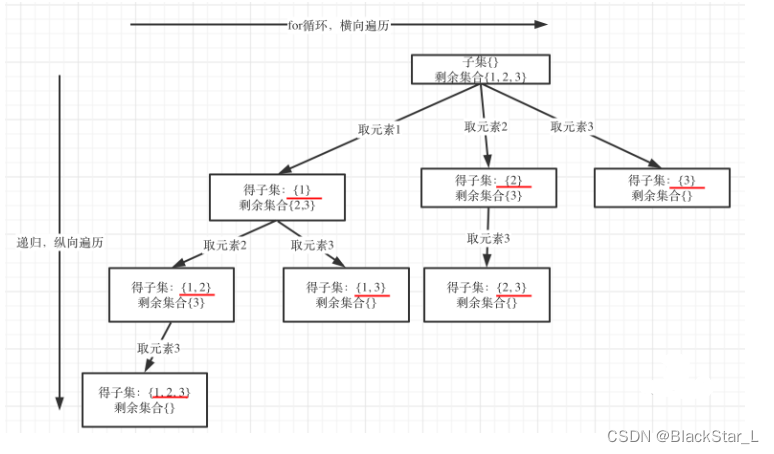
从上图可知,求取子集问题,不需要任何剪枝,因为子集就是要遍历整棵树。
2.3.2、90. 子集 II - 乱序+重复元素+去重复值
力扣题目链接
思路同 40. 数组总和 II,即去重,去掉同一树层的重复节点。
回溯法:
class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(startIndex):res.append(path[:])if startIndex == len(nums):returnfor i in range(startIndex, len(nums)):# 同一树层,相似的则先去掉if i>startIndex and nums[i]==nums[i-1]:continuepath.append(nums[i])backtracking(i+1)path.pop()# 需要排序,便于把相似的排到一起nums.sort()backtracking(0)return res

注意: 一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
子集题做完建议试试 2.6.1、491.递增子序列
class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(ind):res.append(path[:])if ind==len(nums):return# 每一层标记重复used = set()for i in range(ind, len(nums)):# 有重复的跳过,前面已经遍历过if nums[i] in used:continue# 按层添加used.add(nums[i])path.append(nums[i])backtracking(i+1)path.pop()# nums.sort()backtracking(0)return res

2.4、排列问题
排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
2.4.1、46.全排列
力扣题目链接
回溯法1,数组截断传递:
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(nums):# 每次传入的nums是变动的,逐渐变为空,所以不能len(path)==len(nums)if not nums:res.append(path[:])return# 从索引0开始,因为每次都要取到所有数for i in range(len(nums)):path.append(nums[i])# 去掉被选中的nums[i],选取其他段拼在一起backtracking(nums[:i]+nums[i+1:])path.pop()backtracking(nums)return res
回溯法2,used数组:
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:res = []path = []# 创建一个flag数组,保存结果,是否使用过used_list = [False]*len(nums)def backtracking(nums, used_list):# 每次传入的nums是固定的,则len(path)==len(nums)if len(path) == len(nums):res.append(path[:])returnfor i in range(len(nums)):# 已经使用过,则去重if used_list[i]==True:continueused_list[i] = Truepath.append(nums[i])backtracking(nums, used_list)used_list[i] = Falsepath.pop()backtracking(nums, used_list)return res
回溯法3,去掉used:
最简单的写法,因为无重复元素,所以path可以代替used_list。
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(nums):# 每次传入的nums是固定的,则len(path)==len(nums)if len(path) == len(nums):res.append(path[:])returnfor i in range(len(nums)):# 因为本题为无重复元素,所以path内的元素是唯一的if nums[i] in path:continuepath.append(nums[i])backtracking(nums)path.pop()backtracking(nums)return res
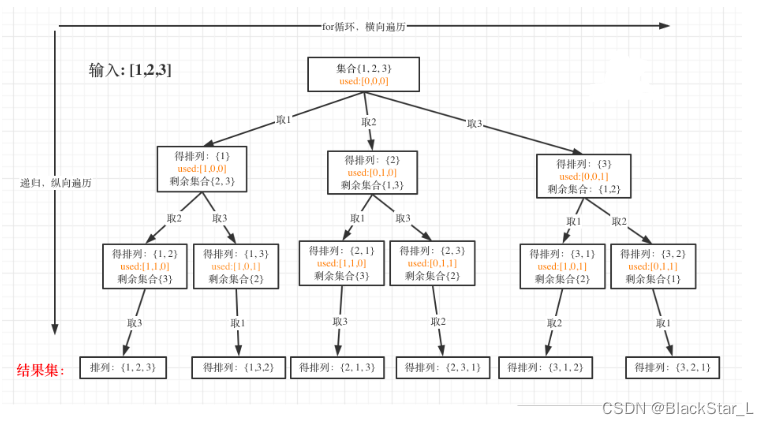
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
排列问题的不同:
每层都是从0开始搜索而不是startIndex
需要used数组记录path里都放了哪些元素了
2.4.2、47.全排列 II
力扣题目链接
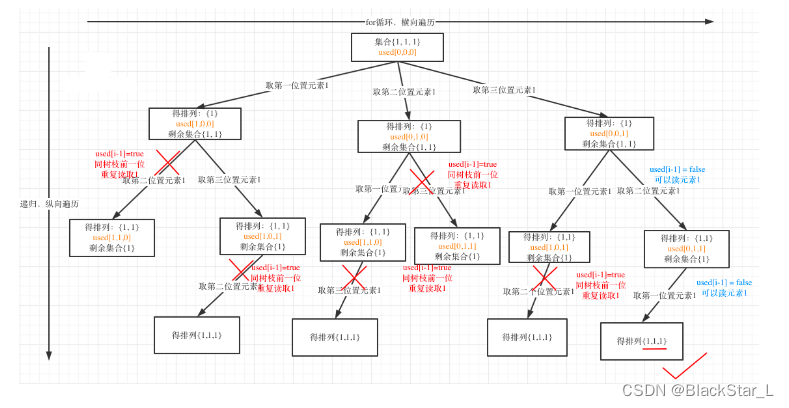
这里必须使用used_list布尔列表,一个是原来的作用,即判断使用使用过;另一个是判断,在同一层,和此元素相同的值之前是否使用过。使用过直接跳过,否则是相同的操作结果。
class Solution:def permuteUnique(self, nums: List[int]) -> List[List[int]]:res = []path = []used_list = [False]*len(nums)def backtracking(nums, used_list):if len(nums) == len(path):res.append(path[:])returnfor i in range(len(nums)):# 每次递归,都是所有元素# 1.该元素自身被使用过,continueif used_list[i] == True:continue# 2.该元素同一层有之前有重复,则只算一次,则这一次continue# used_list[i-1]==True表示同一层之前使用过# 同一层去重效率高,即取False效率比True高if (i>0 and nums[i]==nums[i-1]) and used_list[i-1]==False:continueused_list[i] = Truepath.append(nums[i])backtracking(nums, used_list)used_list[i] = Falsepath.pop()nums.sort()backtracking(nums, used_list)return res

2.5、应用型类似问题
2.5.1、491.递增子序列 (和子集问题很像)- 非排序+重复元素+去重
力扣题目链接
本题求自增子序列,是不能对原数组经行排序的,排完序的数组都是自增子序列了,所以不能使用之前的去重逻辑!
回溯法+集合去重:
#深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(startIndex):if len(path)>=2:res.append(path[:])if startIndex==len(nums):return# 这里要放在内部,因为每一层子树都要去重# 用来记录非重复的元素,用来去重判断used_list = set()# 单层递归逻辑# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用for i in range(startIndex, len(nums)):# 这个去重只能判断排序后相邻的数组# 所以像[4,7,6,7]在这里不可用#if i>startIndex and if nums[i] == nums[i-1]:# continue# path非空,且后一个小于前一个,即小于path的最后一个元素 # 或者 同一树层后面重复出现,不同于前面的相邻重复出现if (path and nums[i]<path[-1]) or nums[i] in used_list:continueused_list.add(nums[i])path.append(nums[i])backtracking(i+1)path.pop()backtracking(0)return res
回溯法+哈希表去重:
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:res = []path = []def backtracking(nums, startIndex):if len(path)>=2:res.append(path[:])if startIndex==len(nums):return# 使用哈希表去重,也就是数组或列表used_list = [False] * 201 # 使用列表去重,题中取值范围[-100, 100]for i in range(startIndex, len(nums)):if (path and nums[i]<path[-1]) or used_list[nums[i]+100]==True:continue# +100,将-100 - 100变为0 - 200used_list[nums[i]+100] = Truepath.append(nums[i])backtracking(nums, i+1)path.pop()backtracking(nums, 0)return res
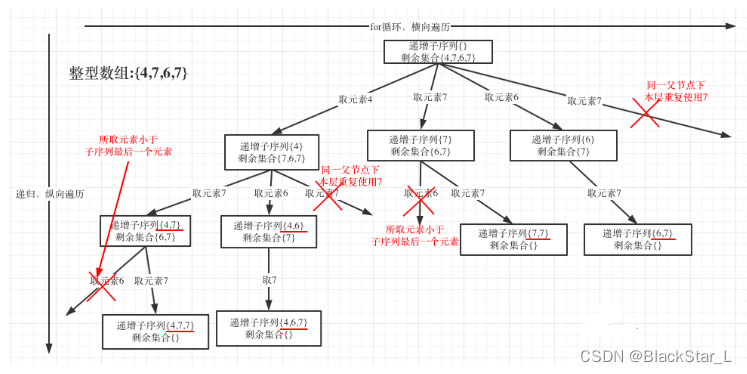
在图中可以看出,同一父节点下的同层上使用过的元素就不能在使用了。与前面的同一层相邻重复的不同。

2.5.2、332.重新安排行程(和2.1.3、17. 电话号码的字母组合 很像)
力扣题目链接
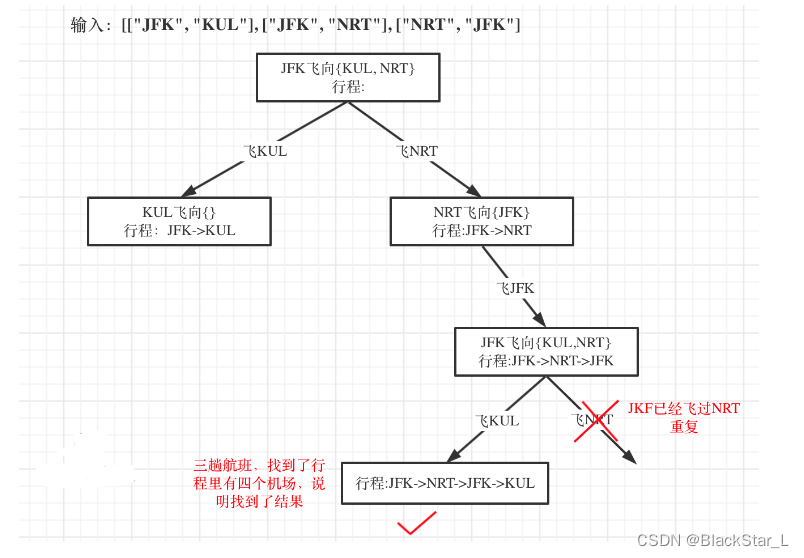
这一题可参考 2.1.3、17. 电话号码的字母组合 - 双层回溯,自己创建映射进行遍历回溯,只不过,电话号码里面,是寻找所有组合,每个数字对于字母的选择是所有,而且能重复选择;而行程里面,每个地点对应的地点列表里,有效的只有部分,并且在选择了某地点后,下一次的地点列表需要将其去除。如何将其去除这是一个难点。
回溯法1(普通解法,超时):
class Solution:def findItinerary(self, tickets: List[List[str]]) -> List[str]:res = []path = []used_list = [False]*len(tickets)def backtracking(tickets):if len(path) == len(tickets):res.append(path[:])return# 每次遍历整个list,前面的通用解法,但对于这一题,这样会超时for i in range(len(tickets)):if used_list[i] == True:continueif i>0 and tickets[i] == tickets[i-1] and used_list[i-1]==True:continueif (path and (path[-1][-1]==tickets[i][0])) or (not path and tickets[i][0] == 'JFK'):used_list[i] = Truepath.append(tickets[i])backtracking(tickets)used_list[i] = Falsepath.pop()backtracking(tickets)# 将结果按字典排序final = sorted(res)[0]r = []# 所有list只取第一个值,加上最后一个list取最后一个值for i in range(len(final)):r.append(final[i][0])if i == len(final)-1:r.append(final[i][1])return r
回溯法2:
重新设置tickets为一个新的对象进行简化处理,这样就无需遍历整个tickets。
class Solution:def findItinerary(self, tickets: List[List[str]]) -> List[str]:res = []path = ['JFK']# 创建一个空字典,值为空listticket_dict = defaultdict(list)for item in tickets:ticket_dict[item[0]].append(item[1])# 排序1 提前排序 或者在内部排序for t in ticket_dict:ticket_dict[t].sort()'''tickets_dict里面的内容是这样的{'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})'''# 根据字典的key去延伸到value再对应到下一个key......以此类推def backtracking(start_point):if len(path) == len(tickets)+1:return True# 内部排序,咱们使用外面的排序方法,只用遍历一次# ticket_dict[start_point].sort()for _ in ticket_dict[start_point]:# 取出一个值,选择一个落地点end_point = ticket_dict[start_point].pop(0)path.append(end_point)# 只要找到一个就可以直接返回了,这里设置成bool# 并且path直接为正确结果,跳过path.pop()还原if backtracking(end_point):return Truepath.pop()ticket_dict[start_point].append(end_point)backtracking('JFK')return path
做回溯相关问题时,先思考以下几点:
排列或组合?有无序?是否有重复元素?有什么不同,需要什么或不需要什么?
总结如下:
| 回溯问题 | 组合 | 排列 | 幂集 |
|---|---|---|---|
| 回溯函数参数 | 使用startIndex,每进一层(startIndex, len(nums)),即找startIndex后面的元素进行组合,防止重复值。 | 任意参数。有重复组合值,只是排列不同,startIndex无意义,使用used布尔列表,为True则表示访问过,去掉。 | 同组合 |
| 额外变量 | 只需startIndex即可 / used布尔list / 同一层的used集合 | used布尔list | 同组合 |
| 遍历顺序 | 从startInde开始搜索:(startIndex, len(nums)) | 从头开始搜索(len(nums) | 同组合 |
| 有重复元素+无序/有序 | (无序则先进行排序)下面三种不同方法排除重复组合,直接continue: [1] i>startIndex and nums[i]==nums[i-1] ;[2] i>0 and nums[i]==nums[i-1] and nums[i-1]=False ;[3] 同一层 used=set() ,nums[i] in used,used只有append无pop。 | (无序则先进行排序)除了自身是否使用过进行判断,其余判断同前面组合,对同一层是否重复使用进行判断。 | 同组合 |
| 无重复元素+无序/有序 | (无需排序)常规回溯写法 | (无需排序)常规回溯写法+used判断/path代替used | 同组合 |
| 结果 | 同长度组合 | 同长度排列 | (不同长度)节点上所有元素。当数组无重复元素,幂集的结果大小为2数组长度2^{数组长度}2数组长度。 |
注意: 这是常规解法,对本文章以及很多特定其他解法没有包含进去,等算法达到了一定的水平可以自行创造。

2.6、棋盘问题

2.6.1、HJ43 迷宫问题
华为机试牛客网链接
回溯法:
# 字符串转数字和迷宫
h, w = map(int, input().split())
maze = []
for i in range(h):maze.append(list(map(int, input().split())))# 初始化
# 起点
result = [(0, 0)]
# 走过的路径进行标记,防止回溯死循环
maze[0][0] = 3# 判断该点是否合法
# 1.范围,2.路或墙
def isVaild(x, y):if 0 <= x < h and 0 <= y < w and maze[x][y] == 0:return Truereturn False# 回溯
def backtracking(x, y):# 打印每一步的坐标点# print(x,y)# 终止条件,到达右下角终点if x == h - 1 and y == w - 1:# result.append((x, y))return result"""回溯前,从第一个方向开始第一个条件先判断下一步是否合法合法再进行深度优先搜索1.同时对走过的路径进行标记为32.将坐标加入到result结果中搜索成功,1和2成立搜索失败,进行回溯:1. 将走过的路径进行回溯,但不能改为原值0,可改为2,另一个值,或者不改也可以2. 将result进行回溯,pop退出结果选择下一个方向如果四个方向都失败,则返回False,说明该方向的深度优先无法走到终点"""# 下if isVaild(x + 1, y):result.append((x + 1, y))maze[x + 1][y] = 3if backtracking(x + 1, y):return True# 回溯result.pop()maze[x + 1][y] = 2# 上if isVaild(x - 1, y):result.append((x - 1, y))maze[x - 1][y] = 3if backtracking(x - 1, y):return True# 回溯result.pop()maze[x - 1][y] = 2# 左if isVaild(x, y - 1):result.append((x, y - 1))maze[x][y - 1] = 3if backtracking(x, y - 1):return True# 回溯result.pop()maze[x][y - 1] = 2# 右if isVaild(x, y + 1):result.append((x, y + 1))maze[x][y + 1] = 3if backtracking(x, y + 1):return True# 回溯result.pop()maze[x][y + 1] = 2# 上下左右都不行,则返回Falsereturn False
backtracking(0, 0)
print(result)
print(maze)
测试输入:
h,w = map(int, '5 5'.split())
maze = []
deal = ['0 1 0 0 0', '0 1 1 1 0', '0 0 0 0 0','0 1 1 1 0','0 0 0 1 0']
for i in deal:maze.append(list(map(int, i.split())))
"""
[[0, 1, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 1, 0]]
"""
结果:
0 0
1 0
2 0
3 0
4 0
4 1
4 2
2 1
2 2
2 3
2 4
3 4
4 4
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 4)]
[[3, 1, 0, 0, 0],[3, 1, 1, 1, 0],[3, 3, 3, 3, 3],[2, 1, 1, 1, 3],[2, 2, 2, 1, 3]]

2.6.2、51. N 皇后
力扣题目链接
回溯法:
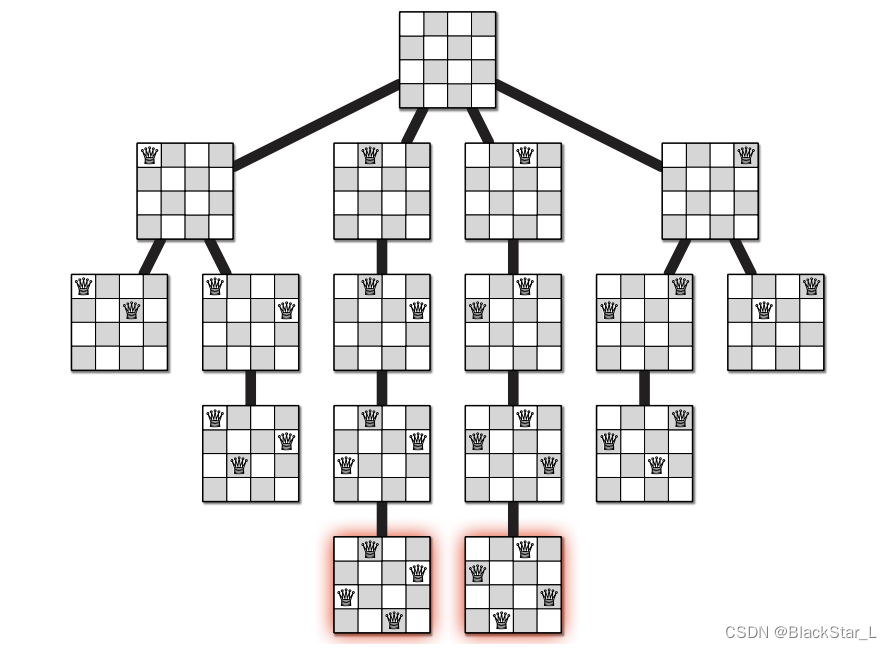
class Solution:def solveNQueens(self, n: int) -> List[List[str]]:res = []board = [['.']*n for _ in range(n)]# 判断是否合法def isVaild(board, row, col):# 1. 判断同一列是否冲突for i in range(row+1):if board[i][col] == 'Q':return False# 2.判断左上是否冲突tmp_row = rowtmp_col = colwhile 0<=tmp_row<n and 0<=tmp_col<n:if board[tmp_row][tmp_col]== 'Q':return Falsetmp_row-=1tmp_col-=1# 3.判断右上是否冲突tmp_row = rowtmp_col = colwhile 0<=tmp_row<n and 0<=tmp_col<n:if board[tmp_row][tmp_col]== 'Q':return Falsetmp_row-=1tmp_col+=1return True# 每一行进行遍历def backtracking(row, board):if row == n:tmp = []for i in board:tmp.append(''.join(i))res.append(tmp)return# 每一行的每一列进行选取for col in range(n):if not isVaild(board, row, col):continueboard[row][col] = 'Q'# 进入下一行backtracking(row+1, board)board[row][col] = '.'backtracking(0, board)return res
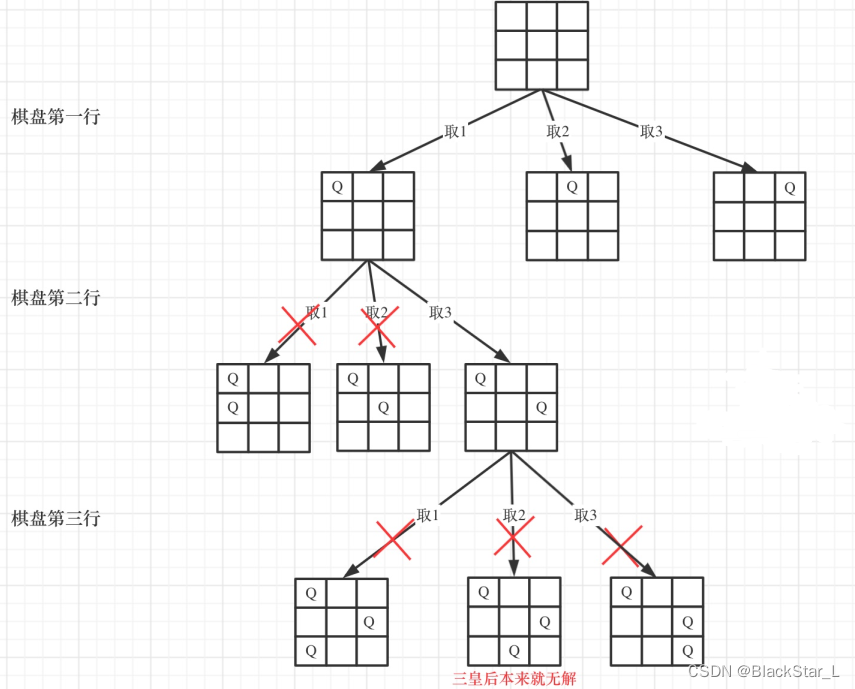
皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
符合条件则继续下一行,否则同行的下一列。
这题是hard题其实难度并不大,当做 2.1.3、17. 电话号码的字母组合 和 332.重新安排行程 来做,每一行为索引进行遍历,内部每一列进行遍历回溯。
难点在于判断条件,即约束条件上是否有Q。我们一般拆成4个部分,横,竖,正斜,反斜,但实际上,横无需判断,因为每一行的行为树根,这个只会按顺序递增,而由此引出子树列才需要回溯,只会产生一个Q。并且斜左下与斜右下也无需遍历,因为一定为空,一定没有Q,因为还没遍历到那个位置,所以咱们的判断以该点为水平线的上面部分为区间即可,这样可以降低复杂度。

2.6.3、37. 解数独
力扣题目链接
回溯法:
class Solution:def solveSudoku(self, board: List[List[str]]) -> None:"""Do not return anything, modify board in-place instead."""def isVaild(row, col, val, board):# 判断同一行是否冲突for i in range(9):if board[row][i] == str(val):return False# 判断同一列是否冲突for i in range(9):if board[i][col] == str(val):return False# 判断同一宫是否冲突start_row = (row//3)*3start_col = (col//3)*3for i in range(start_row, start_row+3):for j in range(start_col, start_col+3):if board[i][j] == str(val):return Falsereturn True# 若有解返回True,无解返回Falsedef backtracking(board):# 这里遍历完即是终止条件# 遍历整个表,行和列for i in range(len(board)):for j in range(len(board[0])):# 若空格内已经有数字,则跳过if board[i][j] != '.':continue# 逐渐填入1-10for k in range(1, 10):# 有效则继续递归if isVaild(i, j, k, board):board[i][j] = str(k)if backtracking(board):return True# 回溯board[i][j] = '.'# 若数字1-9都不能成功填入空格,返回False无解return False# 有解,说明已经填满了,到了最后一步,所有的board[i][j] != '.'return Truebacktracking(board)
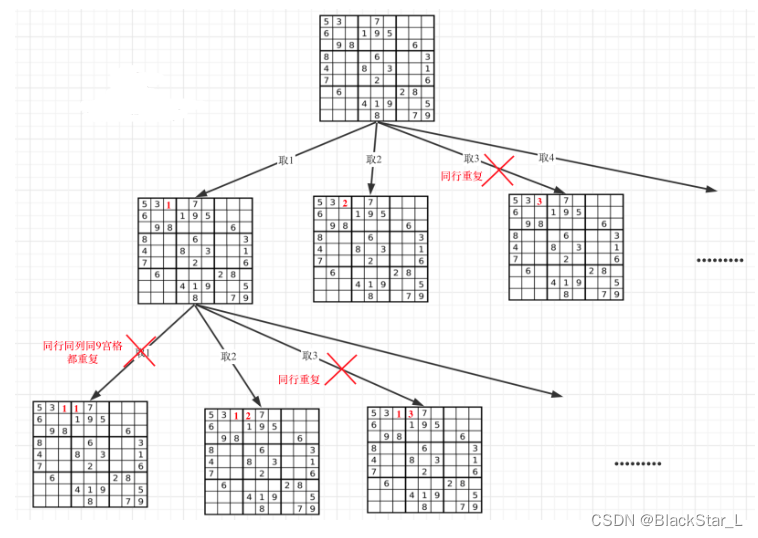
N皇后问题是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
这里需要的是一个二维的递归(也就是两个for循环嵌套着递归),这个二维的递归与下一章中的深搜与广搜有很深的联系,如果你能理解其一,对这题或者下一章的题目的理解都非常的简单。
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性。如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解。
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
同时,一定要注意,最后的两层循环之外,需要return True,因为棋盘都填满了,这是满足结果的,需要传回布尔True给if backtracking()去判断,从而继续return True,防止后续的回溯而还原结果,导致即便搜到了结果,因为回溯还原了,最后board还是原来的空的。
同时,题目要求只有一个结果时,我们把backtracking当做布尔if去判断,通过return True防止回溯。
当题目要求有多个结果时,我们就当普通的backtracking为一行,回溯前将结果通过path存到res中。
三、深搜DFS与广搜BFS
深广搜问题相比回溯问题,少了退回的操作,但思路大致相似,所以该类型题目会更加容易。
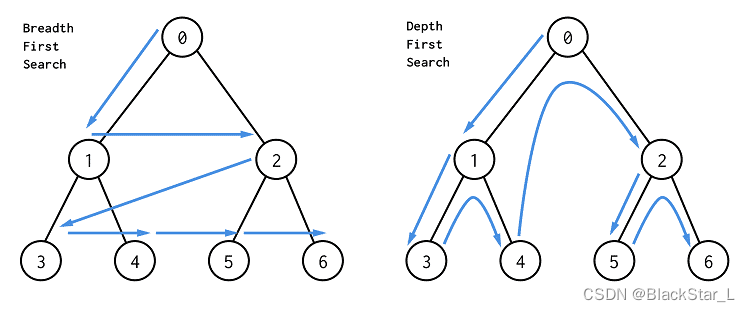
3.1、岛屿问题
基本上,能用dfs做的题目也能用bfs来做,所以可以尝试用这两种方法去解题。这样对该类型算法的理解会更加深刻。

200. 岛屿数量
200. 岛屿数量
非常常规和经典的DFS和BFS题目。
1. 深度优先搜索DFS
dfs题目的模板与回溯法类似,但是没有退回操作,因为都是有效操作。
class Solution:def numIslands(self, grid: List[List[str]]) -> int:# 避免重复,将结果存进来,或者grid[i][j]=0遍历过变成湖泊避免死循环grid_set = set()res = 0def dfs(i, j):for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1' and (x,y) not in grid_set:# 遍历过的结果存到grid_setgrid_set.add((x,y))# 将符合条件的(x,y)继续迭代dfs(x,y)for i in range(len(grid)):for j in range(len(grid[0])):# 为陆地,并且没被遍历过if grid[i][j]=='1' and (i,j) not in grid_set:res+=1grid_set.add((i,j))dfs(i,j)return res
因为整个地图给到我们,我们不用将结果存起来去判断重复,直接遍历过的变成 0 湖泊就行了,那么少一个grid_set的空间以及搜索时间,效率会提高:
class Solution:def numIslands(self, grid: List[List[str]]) -> int:res = 0def dfs(i, j):grid[i][j]='0' # 这里改成非'1'的任何值都可以for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1':# 将符合条件的(x,y)继续迭代dfs(x,y)for i in range(len(grid)):for j in range(len(grid[0])):# 为陆地,并且没被遍历过if grid[i][j]=='1':res+=1dfs(i,j)return res
2. 广度优先搜索 BFS
from collections import deque
class Solution:def numIslands(self, grid: List[List[str]]) -> int:res = 0for i in range(len(grid)):for j in range(len(grid[0])):# 为陆地,并且没被遍历过if grid[i][j]=='1':res+=1grid[i][j]=='0'# 用队列代替列表存储,加快速度neighbors = deque([(i,j)])# 从一个点开始向周围扩散,广度优先,扩散到完成,退出,找下一个点while neighbors:# 从左起点开始取所有点# 为什么从左开始?先搜索完该点的第一外层# 随后第二外层等等依次继续xi, yj = neighbors.popleft()# 后面的代码同dfs,但是内部没有嵌套dfs,也就不会无限的深度找,而是找一次,即外层一圈即可。for x, y in (xi+1, yj), (xi-1, yj), (xi, yj+1), (xi, yj-1):if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1':neighbors.append((x, y))grid[x][y]='0'return res
1254. 统计封闭岛屿的数目
1254. 统计封闭岛屿的数目
求封闭的个数,那么分为非封闭与封闭岛屿,需要在搜索的过程中对不符合条件的进行标记,被标记上的岛屿总数不会+1。
1.深度优先搜索DFS
遍历所有面积,去除与边界连通的面积,即边界位置有1岛屿的。
class Solution:def closedIsland(self, grid: List[List[int]]) -> int:row = len(grid)col = len(grid[0])res = 0def dfs(i, j):# 同样,遍历过的点进行标注,防止死循环或重复遍历grid[i][j]=1for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):if 0<=x<row and 0<=y<col and grid[x][y]==0:# 有不符合条件的点,该面积标注为0,即不合理if x==0 or x==row-1 or y==0 or y==col-1:nonlocal flagflag=0dfs(x, y)for i in range(1, row-1):for j in range(1, col-1):flag = 1if grid[i][j]==0:dfs(i, j)# 符合条件,无边界为0或row、col长度的面积则合理if flag:res+=1return res
2.广度优先搜索
from collections import deque
class Solution:def closedIsland(self, grid: List[List[int]]) -> int:row = len(grid)col = len(grid[0])res = 0for i in range(1, row-1):for j in range(1, col-1):flag = 1if grid[i][j]==0:grid[i][j]=1# 同样使用队列代替列表加速neighbors = deque([(i, j)])while neighbors:xi, yj = neighbors.popleft()for x, y in (xi+1, yj),(xi-1, yj),(xi,yj+1),(xi,yj-1):if 0<=x<row and 0<=y<col and grid[x][y]==0:# 判断条件,不符合条件的标记为0if x==0 or x==row-1 or y==0 or y==col-1:flag = 0# 添加下一圈点以及避免重复进行相反值标记neighbors.append((x,y))grid[x][y]=1# 符合条件,无边界为0或row、col长度的面积则合理if flag:res+=1return res
3.深度优先/广度优先 去除边界连通面积
class Solution:def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:row = len(grid1)col = len(grid1[0])res = 0# 常规dfsdef dfs(i,j):grid2[i][j]=0for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):if 0<=x<row and 0<=y<col and grid2[x][y]==1:dfs(x ,y)# 求B在A中的子集,B有A没有的点,延伸的面积全部变成0for i in range(row):for j in range(col):if grid1[i][j]==0 and grid2[i][j]==1:dfs(i,j)# 最后剩下的grid2中的1的岛屿即A的子集for i in range(row):for j in range(col):if grid2[i][j]==1:res+=1dfs(i,j)return res
1020.飞地的数量
1020.飞地的数量
这题同上思路,不过不是统计面积,无需再dfs,而是统计为1的格子数量,那么直接遍历即可。
class Solution:def numEnclaves(self, grid: List[List[int]]) -> int:row = len(grid)col = len(grid[0])res = 0# 同上def dfs(i,j):grid[i][j]=0for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):if 0<=x<row and 0<=y<col and grid[x][y]==1:dfs(x,y)for i in range(row):if grid[i][0]==1:dfs(i,0)if grid[i][col-1]==1:dfs(i,col-1)for j in range(col):if grid[0][j]==1:dfs(0,j)if grid[row-1][j]==1:dfs(row-1,j)# 统计图上都是1的格子数量for i in range(1, row-1):for j in range(1, col-1):if grid[i][j]==1:res+=1return res
广度优先的写法也很简单,同上。
695. 岛屿的最大面积
695. 岛屿的最大面积
同前面,将所有面积计算出来,每次max最大的即可。
1.深度优先搜索DFS
class Solution:def maxAreaOfIsland(self, grid: List[List[int]]) -> int:row = len(grid)col = len(grid[0])# 保存最大的结果max_area = 0def dfs(i,j):grid[i][j]=0# 这里是关键,每遍历一个点,面积+1nonlocal areaarea+=1for x, y in (i+1, j),(i-1,j),(i,j+1),(i,j-1):if 0<=x<row and 0<=y<col and grid[x][y]==1:dfs(x,y)for i in range(row):for j in range(col):if grid[i][j]==1:area = 0dfs(i,j)# 取最大的面积max_area = max(max_area, area)return max_area
2.广度优先搜索 BFS
from collections import deque
class Solution:def maxAreaOfIsland(self, grid: List[List[int]]) -> int:row = len(grid)col = len(grid[0])max_area = 0for i in range(row):for j in range(col):if grid[i][j]==1:area = 0grid[i][j]=0neighbors = deque([(i,j)])while neighbors:xi, yj = neighbors.popleft()# 面积+1area+=1for x, y in (xi+1, yj), (xi-1, yj), (xi, yj+1),(xi,yj-1):if 0<=x<row and 0<=y<col and grid[x][y]==1:neighbors.append((x,y))grid[x][y]=0max_area = max(area, max_area)return max_area
1905. 统计子岛屿
1905. 统计子岛屿
class Solution:def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:row = len(grid1)col = len(grid1[0])res = 0def dfs(i,j):grid2[i][j]=0for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):if 0<=x<row and 0<=y<col and grid2[x][y]==1:dfs(x ,y)# 求B在A中的子集,B有A没有的点,延伸的面积全部变成0for i in range(row):for j in range(col):if grid1[i][j]==0 and grid2[i][j]==1:dfs(i,j)# 最后剩下的grid2中的1的岛屿即A的子集for i in range(row):for j in range(col):if grid2[i][j]==1:res+=1dfs(i,j)return res
广度优先的写法也很简单,同上。
130. 被围绕的区域
130. 被围绕的区域
class Solution:def solve(self, board: List[List[str]]) -> None:row = len(board)col = len(board[0])def dfs(i,j):board[i][j]='Z'for x, y in (i+1, j),(i-1, j),(i, j+1),(i,j-1):if 0<=x<row and 0<=y<col and board[x][y]=='O':dfs(x,y)# 两竖边界for i in range(row):if board[i][0]=='O':dfs(i,0)if board[i][col-1]=='O':dfs(i,col-1)# 两横边界for j in range(col):if board[0][j]=='O':dfs(0,j)if board[row-1][j]=='O':dfs(row-1,j)for i in range(row):for j in range(col):if board[i][j]=='O':board[i][j]='X'if board[i][j]=='Z':board[i][j]='O'
广度优先的写法也很简单,同上。
417. 太平洋大西洋水流问题
417. 太平洋大西洋水流问题
这题也是需要判断区域的四个边界,以此为判断能否流出两种河流的结果。
除此之外,该题的图内的值不可更改,所以需要另外创建visited去存储访问过的点,visited可以为图大小的二维数组,也可以为set集合或者list列表。
class Solution:def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:row = len(heights)col = len(heights[0])res = []def dfs(i,j):visited.add((i,j))if i==0 or j==0:nonlocal sign_pacificsign_pacific = 1if i==row-1 or j==col-1:nonlocal sign_atlanticsign_atlantic = 1if sign_pacific and sign_atlantic:return Truefor x,y in (i+1, j),(i-1,j),(i,j+1),(i,j-1):if 0<=x<row and 0<=y<col:if heights[x][y]<=heights[i][j] and (x,y) not in visited:dfs(x, y)for i in range(row):for j in range(col):sign_pacific = 0sign_atlantic = 0# 不能改变原图的值,所以避免重复值,则需要新创建一个图visited = set()dfs(i,j)if sign_pacific and sign_atlantic:res.append([i,j])return res
3.2、集合划分问题(等用于回溯的问题)
698. 划分为k个相等的子集
698. 划分为k个相等的子集
要划分相等子集,首先要判断能否划分,即能否被k整除,能的话再继续下一步判断。
k个子集相当于k个桶,将nums的物品依次丢入到这k个桶中去,每一个可能放可能不放复杂度为O(kn)O(k^n)O(kn)相当于暴力搜索。
按序深搜每个物品放入每个桶中,能放入该桶,则深搜下一个物品,不能则回溯,放入下一个桶中。如果每个桶都不能放,则退出了k个桶的循环return False。
class Solution:def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:target = sum(nums)if target%k:return Falsetarget //=k# 优化1,将nums物品按照从大道小排序,可减少搜搜复杂度。# 如果物品大小大于背包,4个桶装不下,可以直接False# 等于背包则直接放入而装满,进行下一个nums.sort(reverse=True)bucket = [0]*kdef dfs(ind):if ind==len(nums):return Truefor i in range(k):# 优化2,如果桶的大小相同,当放一个物品放不下时,放另一个相等大小的桶也一样放不下,则直接跳过不一样大小的桶进行dfsif i>0 and bucket[i]==bucket[i-1]:continue# 优化3(这里没更改),if bucket[i]+nums[ind]<=target:再继续后面的# 把 if bucket[i]<=target and dfs(ind+1): 拆开bucket[i]+=nums[ind]if bucket[i]<=target and dfs(ind+1):return Truebucket[i]-=nums[ind]return Falsereturn dfs(0)
473. 火柴拼正方形
473. 火柴拼正方形
class Solution:def makesquare(self, matchsticks: List[int]) -> bool:target = sum(matchsticks)if target%4:return Falsetarget //=4bucket = [0]*4matchsticks.sort(reverse=True)def backtracking(ind):if ind==len(matchsticks):return Truefor i in range(4):if i>0 and bucket[i]==bucket[i-1]:continuebucket[i]+=matchsticks[ind]if bucket[i]<=target and backtracking(ind+1):return Truebucket[i]-=matchsticks[ind]return Falsereturn backtracking(0)2305. 公平分发饼干
2305. 公平分发饼干
以cookies =[8,15,10,20,8]和k=2为例
相当于吧所有的方法找出来:
[61, 0]
[53, 8]
[41, 20]
[33, 28]
[51, 10]
[43, 18]
[31, 30]
[23, 38]
[46, 15]
[38, 23]
[26, 35]
[18, 43]
[36, 25]
[28, 33]
[16, 45]
[8, 53]
去找bucket里的最大值,整体的最小值:
res = min(res, max(bucket))
因为复杂度很高,再进行剪枝
import math
class Solution:def distributeCookies(self, cookies: List[int], k: int) -> int:# 因为可能无法均分,所以这里不去设置target值,而是设置一个变动的res# res逐渐变小,但是是bucket里的最大值# target = sum(cookies)# target = math.ceil(target/k)# 从最大值开始,找最小值,因为小就接近于均分 res = float('inf')# 优化1cookies.sort(reverse=True)bucket = [0]*kdef backtracking(ind):if ind==len(cookies):# print(bucket)nonlocal resres = min(res, max(bucket))returnfor i in range(k):# 优化2if i>0 and bucket[i]==bucket[i-1]:continue# 优化3 剪枝,有桶大于res,直接去掉if bucket[i]+cookies[ind]<res:bucket[i]+=cookies[ind]backtracking(ind+1)bucket[i]-=cookies[ind]backtracking(0)return res
1723. 完成所有工作的最短时间
1723. 完成所有工作的最短时间
class Solution:def minimumTimeRequired(self, jobs: List[int], k: int) -> int:res = float('inf')bucket = [0]*kjobs.sort(reverse=True)def backtracking(ind):if ind==len(jobs):nonlocal resres = min(res, max(bucket))return Truefor i in range(k):if i>0 and bucket[i]==bucket[i-1]:continueif bucket[i]+jobs[ind]<res:bucket[i]+=jobs[ind]backtracking(ind+1)bucket[i]-=jobs[ind]return Falsebacktracking(0)return res3.3、其他问题
547. 省份数量
547. 省份数量
这题是以一个表来展现相邻,这与岛的相邻不同,不能直接判表中的1相邻,实际上咱们每一行站在列的角度,行的列不相交,则不会直接相邻,可能间接相邻,需要深度搜索,若相交则一定相邻。当然这只是个思考判断方法,具体做题是另一种思路。
这里行与列一定相等,把坐标表示为城市名字。
遍历每一行,即从第一个城市开始探索与其相邻的城市,第一行是与0节点相连的所有其他城市,值为1则对其显示的列坐标城市,转到对应的行再进行深度搜索,寻找与其相邻的城市,重复该步骤,并且用visited进行存储,已经存在则无需重复再搜。
class Solution:def findCircleNum(self, isConnected: List[List[int]]) -> int:row = len(isConnected)col = len(isConnected[0])res = 0def dfs(i):visited.add(i)for j in range(row):if j not in visited and isConnected[i][j]==1:dfs(j)visited = set()for i in range(row):if i not in visited:dfs(i)res+=1print(visited)return res深广搜问题相比回溯问题更加的简单,并且都有相似且固定的模板,相信你通过这篇文章,能对回溯与深广搜有了较为深刻的学习和认识!
参考
Fairly Nerdy
carlprogramming
相关文章:

算法刷题总结 (二) 回溯与深广搜算法
算法总结2 回溯与深广搜算法一、理解回溯算法1.1、回溯的概念1.2、回溯法的效率1.3、回溯法问题分类1.4、回溯法的做题步骤二、经典问题2.1、组合问题2.1.1、77. 组合 - 值不重复2.1.2、216.组合总和III - 值不重复且等于目标值2.1.3、17. 电话号码的字母组合 - 双层回溯2.1.4、…...

Linux 总结9个最危险的命令,一定要牢记在心!
rm -rf 命令 该命令可能导致不可恢复的系统崩坏。 rm -rf / #强制删除根目录下所有东西。 rm -rf * #强制删除当前目录的所有文件。 rm -rf . #强制删除当前文件夹及其子文件夹。 执行rm -rf 一定要想半天,搞明白自己在干什么. fork 炸弹 😦) { 😐:&am…...
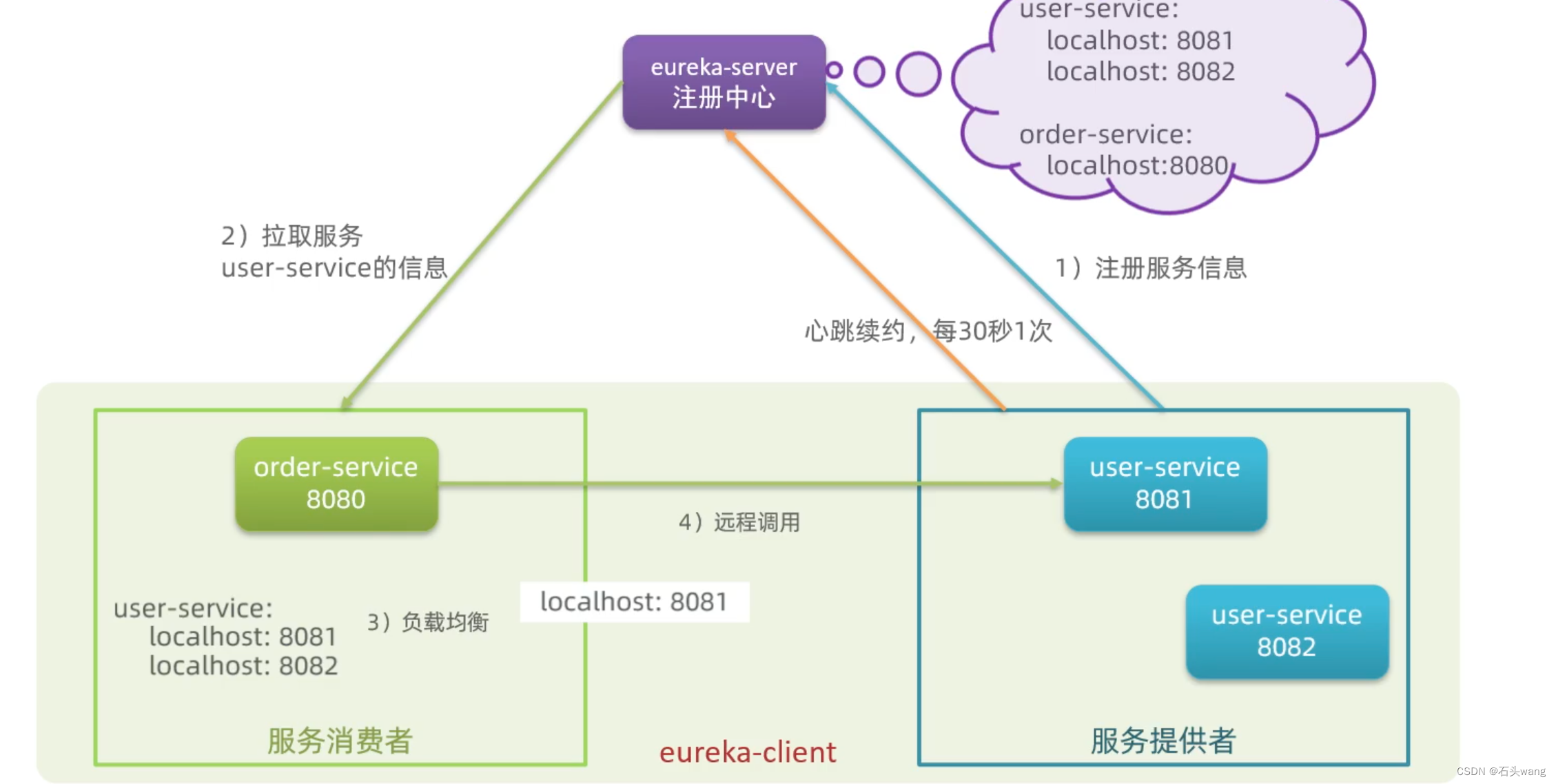
spring cloud
spring cloud 分享 springboot:可以说是spring cloud的基础,是springMVC框架的简化,约定大于配置(在使用上、非功能上的简化) 可以说每个MPO Digital api就是springboot project(springboot项目) spring cloud…...

【9】核心易中期刊推荐——图像视觉与图形可视化
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

0108Bean销毁-Bean生命周期详解-spring
Bean使用阶段,调用getBean()得到bean之后,根据需要,自行使用。 1 销毁Bean的几种方式 调用org.springframework.beans.factory.support.AbstractAutowireCapableBeanFactory#destroyBean调用org.springframework.beans.factory.config.Conf…...

微信小程序可以进行dom操作吗?
小程序不能使用各种浏览器暴露出来的 DOM API,进行 DOM 选中和操作 原因:在小程序中,渲染层和逻辑层是分开的,分别运行在不同的线程中,逻辑层运行在 JSCore 中,并没有一个完整浏览器对象,因而缺…...

昇腾AI深耕沽上:港口辐射力之后,天津再添基础创新辐射力
作者 | 曾响铃 文 | 响铃说 AI计算正在以新基建联动产业集群的方式,加速落地。 不久前,天津市人工智能计算中心正式揭牌,该中心整体规划300P算力,2022年底首批100P算力上线投入运营,并实现上线即满载。 这是昇腾AI…...
基于YOLOv5的疲劳驾驶检测系统(Python+清新界面+数据集)
摘要:基于YOLOv5的疲劳驾驶检测系统使用深度学习技术检测常见驾驶图片、视频和实时视频中的疲劳行为,识别其闭眼、打哈欠等结果并记录和保存,以防止交通事故发生。本文详细介绍疲劳驾驶检测系统实现原理的同时,给出Python的实现代…...

【Linux】-- 进程优先级和环境变量
目录 进程的优先级 基本概念 如何查看优先级 PRI与NI NI值的设置范围 NI值如何修改 修改方式一 : 通过top指令修改优先级 修改方式二 : 通过renice指令修改优先级 进程的四个重要概念 环境变量 基本概念 常见的环境变量 查看环境变量 三种…...
iOS 紧急通知
一般通知 关于通知的各种配置和开发,可以参考推送通知教程:入门 – Kodeco,具有详细步骤。 紧急通知表现 紧急通知不受免打扰模式和静音模式约束。当紧急通知到达时,会有短暂提示音量和抖动(约2s)。未锁…...

即时零售:不可逆的进化
“人们经常问我,这个世界还是平的吗?我经常跟他们说,亲爱的,它真的是平的,比以前更平了。”2021年3月,《世界是平的》作者托马斯弗里德曼在演讲时说。如他所说,尽管逆全球化趋势加剧,…...

零售数据总结经验:找好关键分析指标和维度
各位数据的朋友,大家好,我是老周道数据,和你一起,用常人思维数据分析,通过数据讲故事。 每逢月末、季末、年终,运营部门的同事又要开始进行年终总结分析。那么,对零售连锁企业来说,…...
从零开始搭建游戏服务器 第一节 创建一个简单的服务器架构
目录引言技术选型正文创建基础架构IDEA创建项目添加Netty监听端口编写客户端进行测试总结引言 由于现在java web太卷了,所以各位同行可以考虑换一个赛道,做游戏还是很开心的。 本篇教程给新人用于学习游戏服务器的基本知识,给新人们一些学习…...

C++中那些你不知道的未定义行为
引子 开篇我们先看一个非常有趣的引子: // test.cpp int f(long *a, int *b) {*b 5;*a 1;return *b; }int main() {int x 10;int *p &x;auto q (long *)&x;auto ret f(q, p);std::cout << x << std::endl;std::cout << ret <&…...
)
java基础面试题(四)
Mysql索引的基本原理 索引是用来快速寻找特定的记录;把无序的数据变成有序的查询把创建索引的列数据进行排序对排序结果生成倒排表在倒排表的内容上拼接上地址链在查询时,先拿到倒排表内容,再取出地址链,最后拿到数据聚簇索引和非…...

@PropertySource使用场景
文章目录一、简单介绍二、注解说明1. 注解源码① PropertySource注解② PropertySources注解2. 注解使用场景3. 使用案例(1)新增test.properties文件(2)新增PropertySourceConfig类(3)新增PropertySourceTe…...

【C语言进阶:刨根究底字符串函数】strtok strerror函数
本节重点内容: 深入理解strtok函数的使用深入理解strerror函数的使用⚡strtok Returns a pointer to the first occurrence of str2 in str1, or a null pointer if str2 is not part ofstr1sep参数是个字符串,定义了用作分隔符的字符集合。第一个参数指…...

西安石油大学C语言期末重点知识点总结
大一学生一周十万字爆肝版C语言总结笔记 是我自己在学习完C语言的一次总结,尽管会有许多的瑕疵和不足,但也是自己对C语言的一次思考和探索,也让我开始有了写作博客的习惯和学习思考总结,争取等我将来变得更强的时候再去给它优化出…...

读《Multi-level Wavelet-CNN for Image Restoration》
Multi-level Wavelet-CNN for Image Restoration:MWCNN摘要一. 介绍二.相关工作三.方法摘要 存在的问题: 在低级视觉任务中,对于感受野尺寸与效率之间的平衡是一个关键的问题;普通卷积网络通常以牺牲计算成本去扩大感受野&#…...

【Linux】安装DHCP服务器
1、先检测网络是否通 get dhcp.txt rpm -qa //查看软件包 rpm -qa |grep dhcp //确定是否安装 yum install dhcp //进行安装 安装完成后 查询 rpm -ql dhcp 进行配置 cd /etc/dhcp 查看是否有遗留dhcpd.conf.rpmsave 删除该文件 cp /usr/share/doc/dhcp-4.1.1/dhcpd.conf.sampl…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
