代码随想录算法训练营第三十六天| 188.买卖股票的最佳时机IV、309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
写代码的第三十六天
买股票,卡卡买股票,就爱买股票。。。
188.买卖股票的最佳时机IV
思路
本题是多次进行买卖,所以根据上题进行修改。
解决问题1:dp数组的含义以及定义?上题定义的事dp[i][0]初始状态,dp[i][1]第一次买入,dp[i][2]第一次卖出,dp[i][3]第二次买入,dp[i][4]第二次卖出;所以本题也是要根据第1-k次进行买入卖出的设置,但是k是不确定的,所以要用for循环定义。
解决问题2:递推公式?上次的递推公式按照第一次第二次的买入卖出进行递推公式的设置,但是本题的k是不确定的,所以将上题的递推公式进行找规律,其实就是买入和卖出两种状态,所以买入dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);卖出dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i])。所以类比一下就可以得出dp[i][j+1] = max(dp[i-1][j+1],dp[i-1][j]-prices[i]) dp[i][j+2] = max(dp[i-1][j+2],dp[i-1][j+1]+prices[i])
解决问题3:dp数组的初始化?for j in range(1,2*k,2): dp[0][j] = -prices[0],j=0时不重要定义为0就行,从1开始奇数时定义为-prices[0]。
解决问题4:循环顺序?for循环从0开始遍历。
正确代码:
class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:if len(prices) == 0:return 0dp = [[0 for _ in range(2*k+1)] for _ in range(len(prices))]for j in range(1,2*k,2):dp[0][j] = -prices[0]for i in range(1,len(prices)):for j in range(0,2*k-1,2):dp[i][j+1] = max(dp[i-1][j+1],dp[i-1][j]-prices[i])dp[i][j+2] = max(dp[i-1][j+2],dp[i-1][j+1]+prices[i])return dp[-1][-1]
309.最佳买卖股票时机含冷冻期
思路
可以多次买卖,但是卖出之后的一天就是冷冻期。
解决问题1:dp数组的含义以及定义?本题的状态大致可分为持股,不持股,冷冻期三种情况,但是对于不持股的情况还可以细分,不持股可以是因为今天刚卖出去,也可以是因为之前就卖出去了,所以分为四种情况:
持股dp[i][0]=max(dp[i-1][0],dp[i][3],dp[i - 1][1] - prices[i]);当前持有股票的最大利润等于前一天持有股票的最大利润或者前一天不持有股票且不处于冷冻期的最大利润减去当前股票的价格
不持股:不处于冷冻期dp[i][1]=(昨天一定是持有股票状态dp[i - 1][0] + prices[i]);当前不持有股票且不处于冷冻期的最大利润等于前一天持有股票的最大利润加上当前股票的价格
不持股:处于冷冻期dp[i][2]=(前一天就卖了dp[i - 1][1],要么是前一天是冷冻期dp[i-1][3],所以结果是max(dp[i - 1][1],dp[i-1][3]));当前不持有股票且处于冷冻期的最大利润等于前一天不持有股票的最大利润或者前一天处于冷冻期的最大利润
不持股,当天卖出后处于冷冻期dp[i][3]=(那就是之前一天刚卖出去所以是之前就卖了不持股,就是情况三dp[i-1][2]);当前不持有股票且当天卖出后处于冷冻期的最大利润等于前一天不持有股票且不处于冷冻期的最大利润
dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i])
dp[i][2] = dp[i-1][0] + prices[i]
dp[i][1] = max(dp[i-1][1], dp[i-1][3])
dp[i][3] = dp[i-1][2]
解决问题2:初始化为多少?dp[0][0]=(第0天买,所以是-prices[i]),dp[0][1]=(第0天不持股,所以为0),dp[0][2]=(第0天不持股=0),dp[0][3]=(第0天冷冻期,所以为0)
解决问题3:返回值是什么?最后一天不一定是最后的最大值,所以不是return[-1][-1],而是要找到最后一天不持有股票的最大值。所以最后输出的是max(dp[n-1][3], dp[n-1][1], dp[n-1][2])。
class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)if n == 0:return 0dp = [[0 for _ in range(4)] for _ in range(n)] dp[0][0] = -prices[0] for i in range(1, n):dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i]) dp[i][2] = dp[i-1][0] + prices[i]dp[i][1] = max(dp[i-1][1], dp[i-1][3]) dp[i][3] = dp[i-1][2] return max(dp[n-1][3], dp[n-1][1], dp[n-1][2])
714.买卖股票的最佳时机含手续费
思路
本题多次买卖,只是多了一个手续费。
解决问题1:dp[][]数组的含义是什么?指的是当前第i位持股或者不持股情况的最大金钱数。
解决问题2:递推公式?分为两种情况,第一种是dp[i][0]也就是第i天持股的最大金钱数(max(dp[i-1][0],dp[i-1][1]-prices[i])),第二种是dp[i][1]也就是第i天不持股的最大金钱数(max(dp[i-1][1],dp[i-1][0]+prices[i]-fee))
正确代码:
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:dp = [[0 for _ in range(2)] for _ in range(len(prices))]dp[0][0] = -prices[0]dp[0][1] = 0for i in range(1,len(prices)):dp[i][0] = max(dp[i-1][0],dp[i-1][1]-prices[i])dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]-fee)return dp[-1][-1]
相关文章:

代码随想录算法训练营第三十六天| 188.买卖股票的最佳时机IV、309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
写代码的第三十六天 买股票,卡卡买股票,就爱买股票。。。 188.买卖股票的最佳时机IV 思路 本题是多次进行买卖,所以根据上题进行修改。 解决问题1:dp数组的含义以及定义?上题定义的事dp[i][0]初始状态,dp[i][1]第一…...

Golang | Leetcode Golang题解之第332题重新安排行程
题目: 题解: func findItinerary(tickets [][]string) []string {var (m map[string][]string{}res []string)for _, ticket : range tickets {src, dst : ticket[0], ticket[1]m[src] append(m[src], dst)}for key : range m {sort.Strings(m[key])…...

Spring Boot - 通过ServletRequestHandledEvent事件实现接口请求的性能监控
文章目录 概述1. ServletRequestHandledEvent事件2. 实现步骤3. 优缺点分析4. 测试与验证小结其他方案1. 自定义拦截器2. 性能监控平台3. 使用Spring Boot Actuator4. APM工具 概述 在Spring框架中,监控接口请求的性能可以通过ServletRequestHandledEvent事件实现。…...

Docker相关配置记录
Docker相关配置记录 换源 {"registry-mirrors": ["https://dockerhub.icu","https://docker.chenby.cn","https://docker.1panel.live","https://docker.awsl9527.cn","https://docker.anyhub.us.kg","htt…...
与INT(11))
MySQL中INT(3)与INT(11)
本文由 ChatMoney团队出品 开篇 在MySQL数据库设计的世界里,数据类型的选择是一项基础而又至关重要的任务。其中,INT数据类型因其广泛的应用和灵活性备受青睐。然而,围绕着INT(3)与INT(11)的具体差异,常常存在一些误解。本文旨在…...
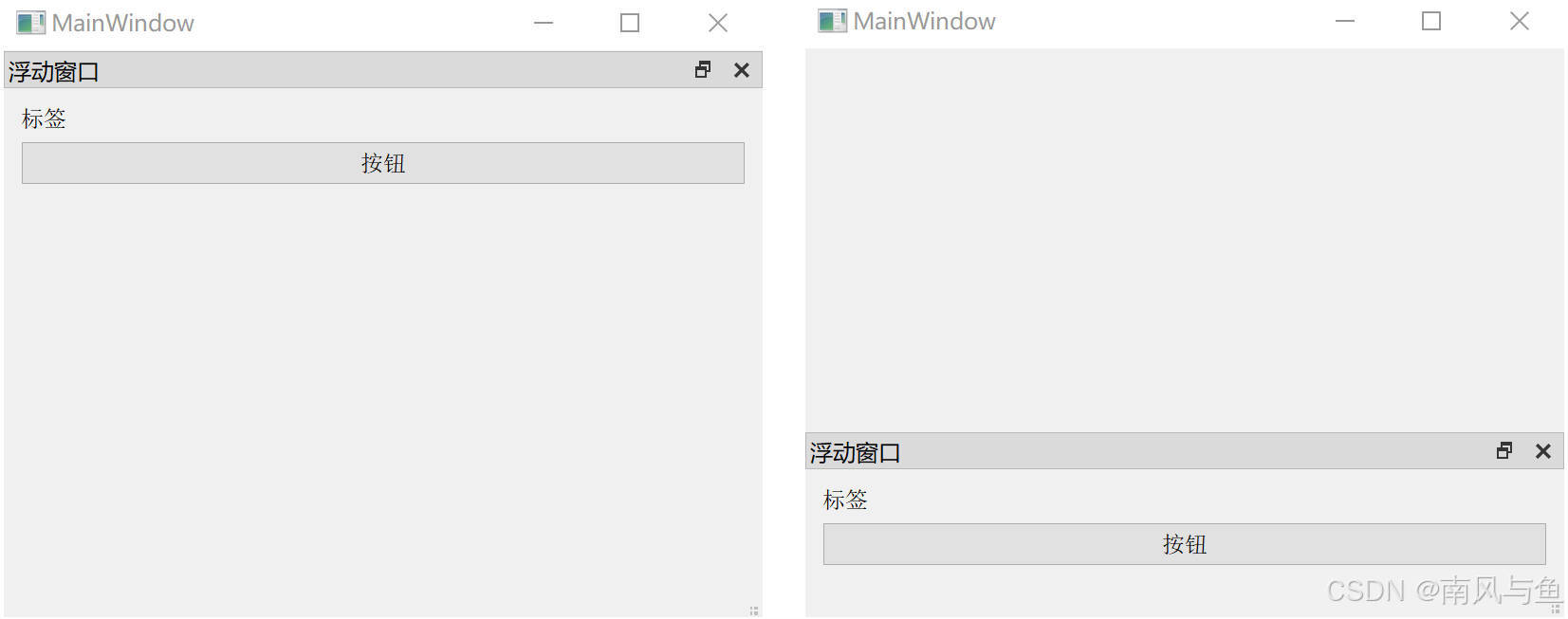
Qt 窗口:菜单、工具与状态栏的应用
目录 引言: 1. 菜单栏 1.1 创建菜单栏 1.2 在菜单栏中添加菜单 1.3 创建菜单项 1.4 在菜单项之间添加分割线 1.5 综合示例 2.工具栏 2.1 创建工具栏 2.2 设置停靠位置 2.3 设置浮动属性 2.4 设置移动属性 3. 状态栏 3.1 状态栏的创建 3.2 在状态栏中显…...
学习必备好物有哪些?高三开学季好物推荐合集
新学期即将开启,学习必备好物有哪些?以下是特别为高三学生朋友们精心挑选的一系列好物推荐,旨在帮助大家在更快更好的选择,快来看看都有哪些吧! 1、书客护眼大路灯Sun 书客是海内外知名的生物光学技术方案商…...

java的分类
目录 Java SE Java EE Java ME java主要分为三类,分别是Java SE,Java EE,Java ME。其中SE是EE和ME的基础。 Java SE 全名为Java Standard Edition,是 Java 平台的基础版本,为开发人员提供了构建和运行桌面应用程…...
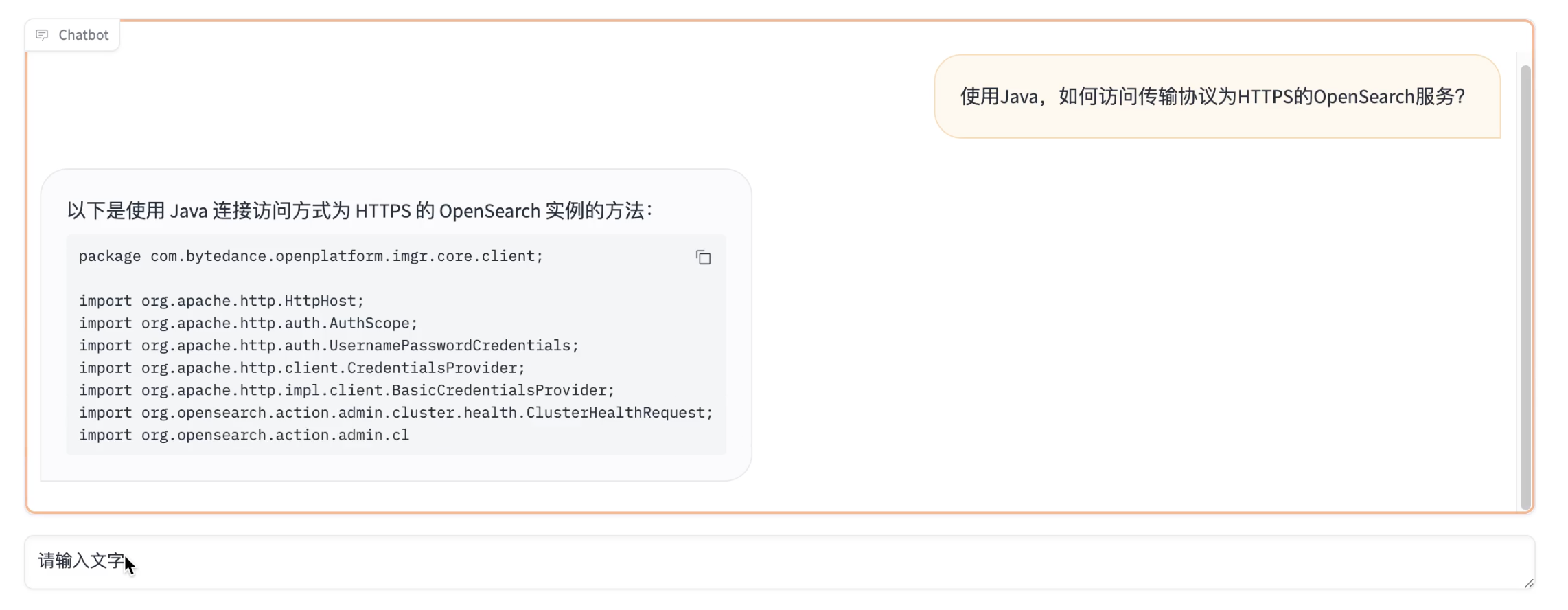
基于火山引擎云搜索服务和豆包模型搭建 RAG 推理任务
大语言模型(LLM,Large language model)作为新一轮科技产业革命的战略性技术,其核心能力在于深层语境解析与知识融合。在生成式人工智能方向主要用于图像生成,书写文稿,信息搜索等。当下的 LLM 模型是基于大…...

Python 实现 Excel 文件操作的技术性详解
目录 一、引言 二、Excel 文件格式及库的选择 2.1 Excel 文件格式 2.2 库的选择 三、安装必要的库 四、使用 openpyxl 读取 Excel 文件 4.1 基本步骤 4.2 实战案例 五、使用 pandas 读取 Excel 文件 5.1 基本步骤 5.2 实战案例 六、写入 Excel 文件 6.1 使用 …...

Spring WebFlux 实现 SSE 流式回复:类GPT逐字显示回复效果完整指南
本节将提供基于 Spring WebFlux 和 SSE 实现类ChatGPT流式回复效果的完整代码示例,并详细说明所需的依赖和配置。 1. 项目配置 构建工具: Maven 或 Gradle依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>sp…...

成功解决7版本的数据库导入 8版本数据库脚本报错问题
我 | 在这里 ⭐ 全栈开发攻城狮、全网10W粉丝、2022博客之星后端领域Top1、专家博主。 🎓擅长 指导毕设 | 论文指导 | 系统开发 | 毕业答辩 | 系统讲解等。已指导60位同学顺利毕业 ✈️个人公众号:热爱技术的小郑。回复 Java全套视频教程 或 前端全套视频…...

如何让RStudio使用不同版本的R
下面内容摘录自: 专栏问答:管理和选择不同的R,如何做好R的笔记_rstudio如何在不同的r版本中进行切换-CSDN博客 欢迎订阅我们专栏 问题一:如何发现RStudio需要安装和使用不同版本的R。这是为什么呢? R允许用户在同一系统…...
汽车免拆诊断案例 | 2011 款进口现代新胜达车智能钥匙系统有时失效
故障现象 一辆2011款进口现代新胜达车,搭载G4KE发动机,累计行驶里程约为26.3万km。车主进厂反映,有时进入车内按下起动按钮,发动机无法起动,且组合仪表黑屏。 故障诊断 接车后试车,车辆使用一切正常。…...

Count clock
写了半天不对,才注意到是十六进制的 - - 另外安装了vivado 哈哈哈哈,可以看看写的到底对不对 之前好多程序在 hdlbits 可以正确运行 但是 vivado 编译不通过。 module clock(input clk,input reset,input ena,output reg pm,output reg[7:0] hh,output …...
【MySQL】1.MySQL基本操作
目录 一、MySQL数据库登陆 1、设置环境变量 2、cmd命令登陆数据库 二、基本操作语法 1、显示数据库——SHOW 2、使用/选择数据库——USE 3、删除——DROP 4、创建——CREATE 5、查看表结构——DESC 6、数据操作——增删改查 (1)增/插入&#…...
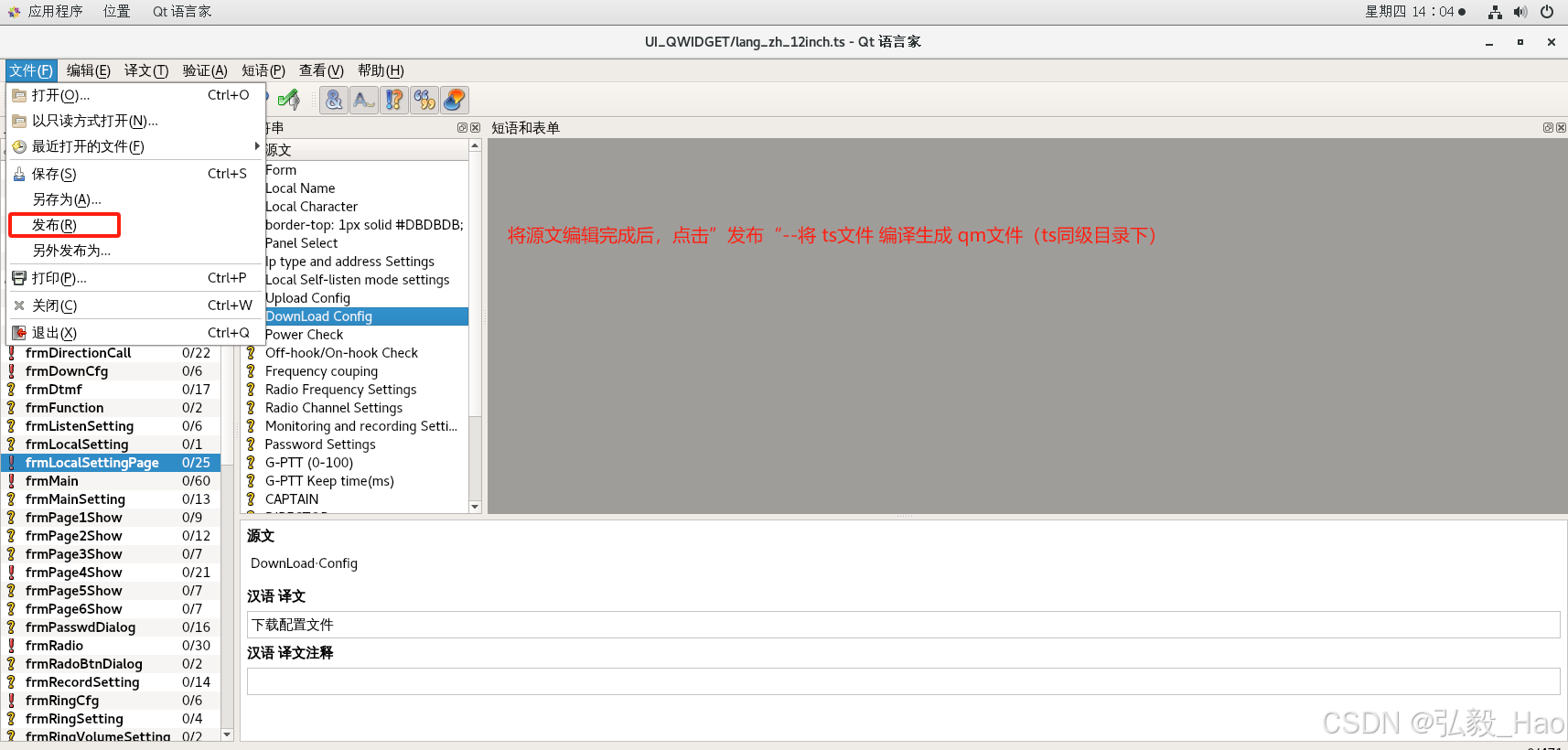
Qt .qm文件详解
Qt中的.qm文件是Qt翻译文件的一种,主要用于支持软件的多语言转换。在生成Qt应用程序时,qm文件会被包含进应用程序中,根据逻辑以显示对应语言的界面。 .qm文件的基本信息 格式:.qm文件是Qt应用程序中用于存储翻译文本的二进制文件…...
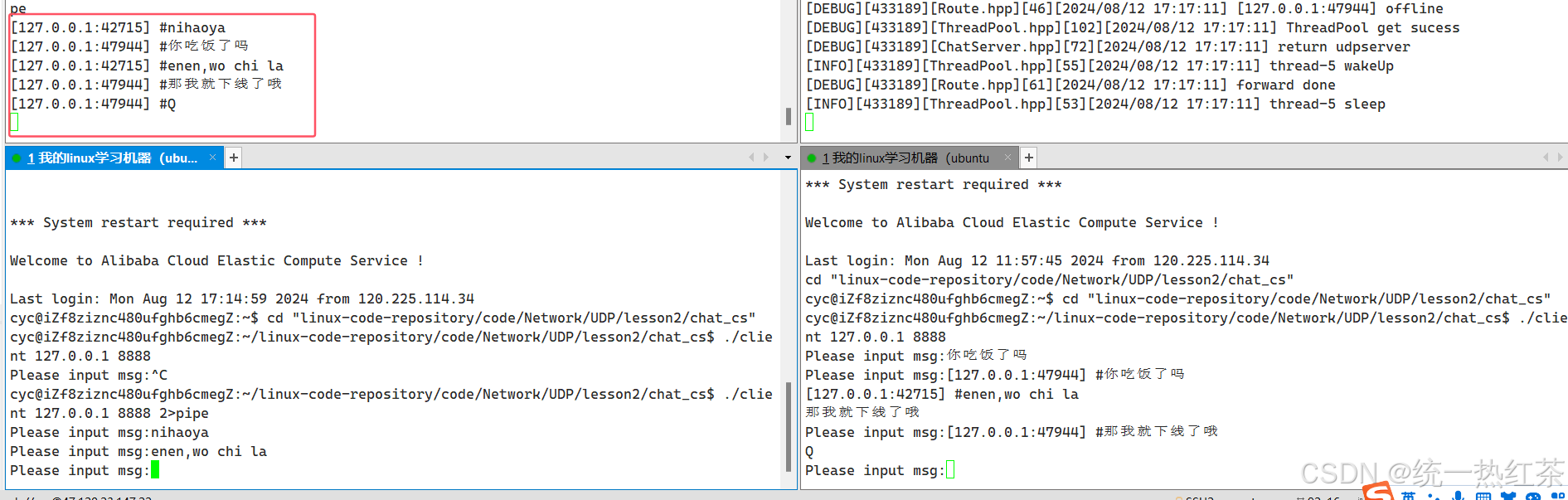
【计算机网络】UDP实战
其实经过这几天写的几种不同的UDP的简易客户端与服务端,还是很有套路的,起手式都是非常像的。 更多的难点对我来说反而是解耦,各种各样的function一用,回调函数一调,呕吼,就会懵一下。 对于这篇文章&#x…...
七、ESP32-S3上使用MicroPython点亮WS2812智能LED灯珠并通过web控制和JS颜色选择器改变灯珠颜色
本地代码集成离线iro.js库来添加一个颜色选择器控件,在无网络环境可以通过JavaScript将选中的颜色发送到服务器以改变LED颜色。以下是将iro.js集成到网页后的颜色图片。 Iro.js 地址API操作手册 color:change # 每当所选颜色发生变化时触发 - 无论是当用户与颜色选…...
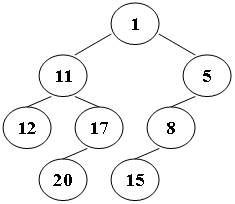
Z 字形遍历二叉树
假设一个二叉树上各结点的权值互不相同。 我们就可以通过其后序遍历和中序遍历来确定唯一二叉树。 请你输出该二叉树的 ZZ 字形遍历序列----也就是说,从根结点开始,逐层遍历,第一层从右到左遍历,第二层从左到右遍历,…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
